Математика Курс для студентов экономических специальностей Мухаметзянов Ирик

Математика Курс для студентов экономических специальностей Мухаметзянов Ирик Зирягович доктор физико-математических наук, профессор кафедры «Математика» , ауд. 3 -212, e-mail: mm_ugntu@mail. ru, 2013 -14 уч. год 1

Неопределенный интеграл

Первообразная

Первообразная

Неопределенный интеграл

Первообразная и неопределенный интеграл

Свойства интеграла, вытекающие из определения Производная неопределенного интеграла равна подынтегральной функции, а его дифференциал- подынтегральному выражению. Действительно:

Свойства интеграла, вытекающие из определения Неопределенный интеграл от дифференциала непрерывно дифференцируемой функции равен самой этой функции с точностью до постоянной: 3. так как является первообразной для

Свойства интеграла

Таблица неопределенных интегралов

Таблица неопределенных интегралов

Свойства дифференциалов При интегрировании удобно пользоваться свойствами:

Примеры

Примеры

Независимость от вида переменной

Пример Вычислим

Методы интегрирования

Интегрирование по частям

Примеры

Примеры

Метод замены переменной

Интегрирование функций, содержащих квадратный трехчлен

Пример

Пример Найти

Квадратичные иррациональности Рассмотрим некоторые типы интегралов, содержащих иррациональные функции. Интегралы типа Называют неопределенными интегралами от квадратичных иррациональностей. Их можно найти следующим образом: под радикалом выделить полный квадрат: и сделать подстановку

При этом первые два интеграла приводятся к табличным, а третий – к сумме двух табличных интегралов. Пример№ 1. Найти интеграл: Решение: Так как

Пример № 2. Найти интеграл : Решение: Выделим полный квадрат : Сделаем подстановку: Тогда:

Интегрирование тригонометрических функций Интегралы вида Находятся с помощью формул:

Пример № 1. Найти интеграл: Решение: Воспользуемся формулой Получим: Тогда

Пример№ 2. Решение: Получим: Тогда Найти интеграл: Воспользуемся формулой:

Пример№ 3. Найти интеграл: Решение: Получим: Тогда: Воспользуемся формулой:

Интегралы типа Для нахождения таких интегралов используются следующие приемы: 1) Подстановка если целое положительное нечетное число; 2) Подстановка если целое положительное нечетное число; 3) Формулы понижения порядка: Если целые неотрицательные четные числа; 4)Подстановка если есть четное отрицательное целое число.

Пример№ 1. Найти интеграл: Решение: Применим подстановку Тогда Получим: Т. к. n=5 (1 cлучай).

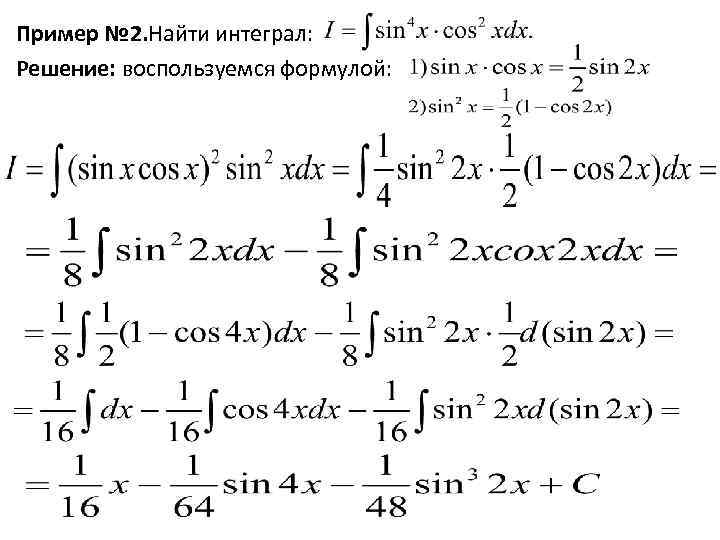Пример № 2. Найти интеграл: Решение: воспользуемся формулой:

Пример № 3. Решение: Здесь Обозначим Получим: Найти интеграл: (4 случай) Тогда

• Универсальная тригонометрическая подстановка Рассмотрим некоторые случаи нахождения интеграла от тригонометрическихфункций. Функцию с переменными и , над которыми выполняются рациональные действия (сложения, вычитание, умножение иделение) Принято обозначать знак рациональной функции. Вычисление неопределённых интегралов типа Сводится к вычислению интегралов от рациональной функции подстановкой , которая называется универсальной

Действительно, Поэтому Где рациональная функция от. Обычно этот способ весьма громоздкий, зато всегда приводит к результату.

На практике применяют и другие, более простые подстановки, в зависимости от свойств ( и вида) подынтегральной функции. В частности, удобны следующие правила: 1)Если функция нечётна относительно Т. е , то подстановка рационализирует интеграл; 2)Если функция нечётна относительно Т. е. , то делается подстановка 3)Если функция четна относительно , то интеграл рационализируется подстановкой. Такая же подстановка применяется, если интеграл имеет вид

Пример: Найти интеграл Решение: Сделаем универсальную подстановку Тогда Следовательно