Математика и статистика МАТЕМАТИКА от греческого

Математика и статистика

МАТЕМАТИКА (от греческого – НАУКА) - наука, в которой изучаются пространственные формы, и количественные отношения действительного мира. СТРУКТУРА (строение , расположение порядок) – совокупность устойчивых связей объекта , обеспечивающая его целостность и тождественность самого себе, т. е. сохранение его основных свойств при различных внешних и внутренних изменениях. Таким образом , МАТЕМАТИЧЕСКАЯ СТРУКТУРА – это пространственные формы, количественные отношения действительного мира, связанные между собой общими основными свойствами при различных внутренних и внешних изменениях.

Общие основные свойства любых пространственных форм, как правило основаны на положениях , применяемых без логического доказательства в силу некоторой убедительности, ИСТИННЫХ ИСХОДНЫХ ПОЛОЖЕНИЯХ которые называются -АКСИОМАМИ . АКСИОМАТИЧЕСКИЙ МЕТОД – способ строения научной теории в виде системы аксиом (постулатов), и правил вывода (аксиоматики) позволяющих путем логической дедукции получать утверждения (теоремы) данной теории.

Статистика (от латинского слова – «статус» ) – означает положение вещей, первоначально употреблялся в значении слова «Государствоведение» , впервые был введен в обиход в 1749 году немецкими учеными. В настоящее время статистика употребляется в трех значениях: -особая отрасль практической деятельности людей, направленную на сбор, обработку и анализ данных -наука , занимающуюся разработкой теоретических положений и методов, используемых статистической практикой -данные, в которых представлены результаты отчетность работы предприятий, организаций, отраслей и т. д.

Особенность статистики в том, что данные сообщаются в количественной форме, т. е. Статистика говорит языком цифр Сбор данных или сведений о социальноэкономических явлениях называется статистическим наблюдением. Набор данных, программа их обработки жестко подчинена нормативно-правовым документам.

Математические способы обработки статистической информации. Основной метод обработки статистического наблюдения в статистике ГРУППИРОВКА - это расчленение единиц статистической совокупности на группы, однородные в какомлибо существенном отношении и характеристику таких групп системой показателей в целях выявления типов явлений, изучения их структуры и взаимосвязей.

Результат группировки - ПОСТРОЕНИЕ ВАРИАЦИОНОГО РЯДА Технология построения вариационного ряда Рассмотрим построение вариационного ряда на примере: ЗАДАЧА 1 ЭТАП - группирования статистических данных- ОПРЕДЕЛЕНИЕ ПРИЗНАКА В результате статистического наблюдения за производственной деятельностью 100 рабочих Получены следующие данные о тарифных разрядах : 2 ЭТАП- РАНЖИРОВАНИЕ статистических данных, т. е – расположение данных в какомлибо порядке, в данном примере в порядке возрастания 3 ЭТАП – СТАТИСТИЧЕСКИЙ АНАЛИЗ – т. е расчет простейших статистических показателей для оценки результативности социально-экономическского явления 5, 1, 4, 5, 4, 3, 35, 5, 2, 5, 5, 6, 4, 3, 1, 5, 2, 5, 5, 5, 3, 3, 3, 6, 6, 5, 3, 4, 5, 4, 6, 6, 5, 2, 1, 5, 4, 5, 5, 3, 6, 4, 5, 5, 4, 3, 5, 5, 5, 4, 5, 6, 1, 5, 2, 6, 4, 4, 3, 5, 6, 2, 5, 4, 5, 5, 4, 6, 5, 2, 5, 3, 4, 5, 6, 5, 5, 3, 5, 4, 6, 6, 5, 5, 4, 5, 5, 6, 5, 5

ПОСТРОЕНИЕ ВАРИАЦИОНОГО РЯДА • 1 ЭТАП - группирования статистических данных. ОПРЕДЕЛЕНИЕ ПРИЗНАКА В данном примере ПРИЗНАКОМ – является тарифный разряд, т. е значения от 1 до 6 Очевидно, что все возможны значения этого признака изолированы и отличаются друг от от друга на конечную величину, такие признаки носят название дискретные

ПОСТРОЕНИЕ ВАРИАЦИОНОГО РЯДА • 2 ЭТАПРАНЖИРОВАНИЕ статистических данных, Т. е – расположение данных в каком-либо порядке, в данном примере в порядке возрастания В результате ранжирования получим следующий ранжированный ряд: • • • 1, 1, 1, 1 – 4 раза 2, 2, 2, 2 – 6 раз 3, …, 3 -12 раз 4, 4, … 4 – 16 раз 5, 5, 5… 5 – 44 раза 6, 6, 6, . . 6 -18 раз

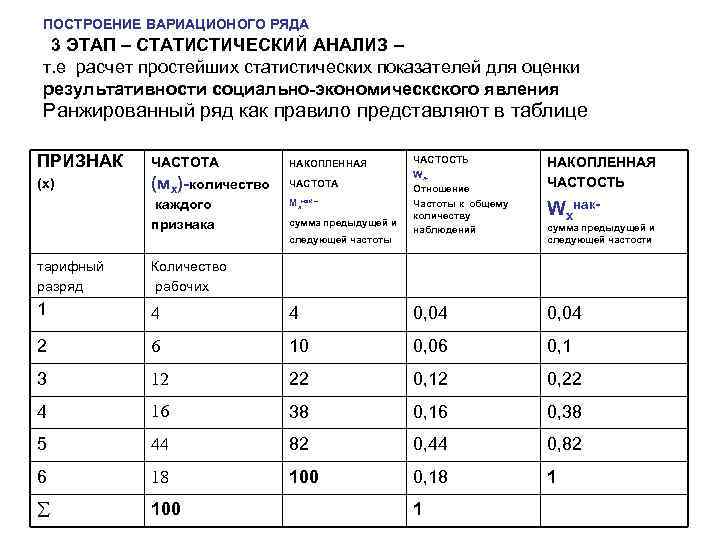ПОСТРОЕНИЕ ВАРИАЦИОНОГО РЯДА 3 ЭТАП – СТАТИСТИЧЕСКИЙ АНАЛИЗ – т. е расчет простейших статистических показателей для оценки результативности социально-экономическского явления Ранжированный ряд как правило представляют в таблице ПРИЗНАК ЧАСТОТА НАКОПЛЕННАЯ (х) (мx)-количество ЧАСТОТА каждого признака Мхнак – сумма предыдущей и следующей частоты ЧАСТОСТЬ Wx. Отношение Частоты к общему количеству наблюдений НАКОПЛЕННАЯ ЧАСТОСТЬ Wxнак- сумма предыдущей и следующей частости тарифный разряд Количество рабочих 1 4 4 0, 04 2 6 10 0, 06 0, 1 3 12 22 0, 12 0, 22 4 16 38 0, 16 0, 38 5 44 82 0, 44 0, 82 6 18 100 0, 18 1 100 1

СТАТИСТИЧЕСКИЙ АНАЛИЗ Полученные статистические показатели позволяют сделать следующие выводы: - о необходимом количестве работником с фиксированным тарифным разрядом - позволяют спланировать фонд заработной платы, налоговые отчисления Наряду с дискретным вариационным рядом существует интервальные вариационные ряды,

Интервальные вариационные ряды – основное отличие интервального ряда от дискретного в том, что признак может принимать значение в некотором числовом интервале. Для построения интервального ряда необходимо • • • определить величину интервала , установить полную шкалу интервалов, сгруппировать результаты наблюдений в соответствии с этой шкалой • в соответствии с технологией построения вариационного ряда ( 3 этапа) провести статистический анализ Задача: Анализируя, результаты работы, в отчетном году структурных 104 подразделений предприятия, получены следующие данные о % выполнения плана: 111, 85, 91, 109, 86, 102, 111, 98, 105, 85, 112, 98, 112, 113, 87, 109, 115, 99, 105, 111, 94, 107, 99, 107, 125, 89, 104, 113, 96, 103, 145, 104, 105, 88, 103, 97, 115, 109, 89, 108, 107, 97, 106, 107, 96, 109, 117, 108, 109, 139, 116, 117, 103, 127, 119, 118, 125, 105, 116, 117, 106, 101, 113, 107, 105, 119, 107, 119, 111, 108, 109, 93, 107, 117, 107, 118, 99, 108, 119, 98, 101, 109, 128, 127, 121, 118, 122, 116, 124, 125, 114, 126, 131, 143

Построение интервального вариационного ряда - определение величины интервала: 1. определить количество n интервальных признаков (формула Стерджесса) n= 1+3, 3221*lq. N (lq – десятичный логарифм, N- количество статистических наблюдений ) на примере задачи: N =104 n= 1+3, 3221*lq 104 = 1+3, 3221*2, 0170= 1+6, 707=7, 707 ~ 8 Þ в интервальном статистическом ряду данные разделены на n = 7 признаков

Построение интервального вариационного ряда 1 определение величины интервала : в соответствии с рассчитанным количеством интервалов n = 7 i(величина интервала)= = Хmax –xmin n В соответствии с условием задачи Хmax = 143 Xmin= 85 i = (143 -85)/ 7=7, 71 8, 2~8

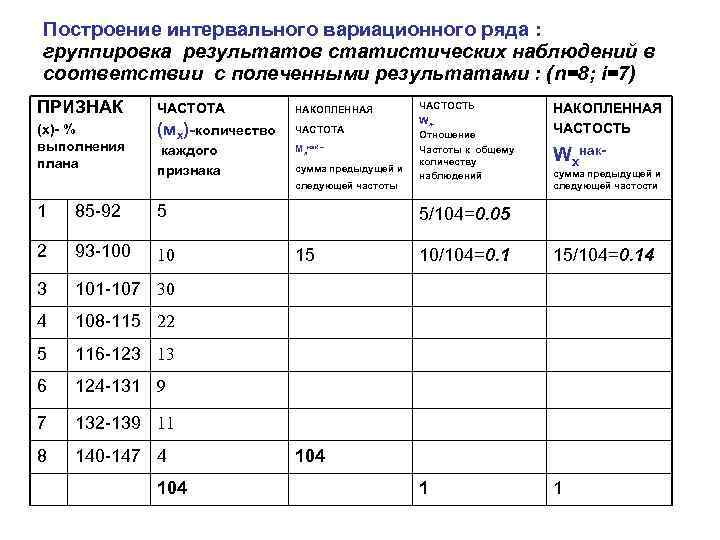Построение интервального вариационного ряда : группировка результатов статистических наблюдений в соответствии с полеченными результатами : (n=8; i=7) ПРИЗНАК ЧАСТОТА НАКОПЛЕННАЯ (х)- % выполнения плана (мx)-количество ЧАСТОТА каждого признака Мхнак – сумма предыдущей и следующей частоты 1 85 -92 5 2 93 -100 10 3 124 -131 9 7 132 -139 11 8 140 -147 4 сумма предыдущей и следующей частости 116 -123 13 6 Wxнак- 108 -115 22 5 НАКОПЛЕННАЯ ЧАСТОСТЬ 101 -107 30 4 ЧАСТОСТЬ Wx. Отношение Частоты к общему количеству наблюдений 104 5/104=0. 05 15 10/104=0. 1 15/104=0. 14 1 1 104

Построение интервального вариационного ряда Основные выводы: -% структурный подразделений выполнивших план - , что составляет - -14 % структурных подразделений не выполнивших план , что составляет - 15 структурных подразделений

Комбинационные группировки в которых одновременно используются дискретные и интервальные технологии построения вариационного ряда

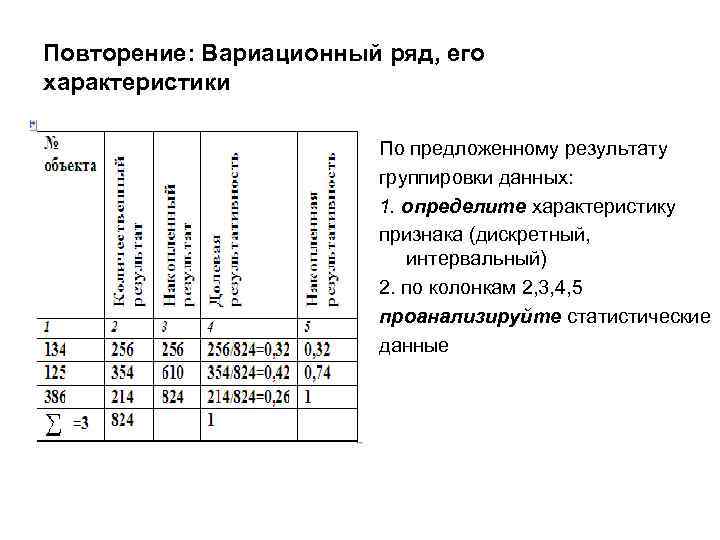Повторение: Вариационный ряд, его характеристики По предложенному результату группировки данных: 1. определите характеристику признака (дискретный, интервальный) 2. по колонкам 2, 3, 4, 5 проанализируйте статистические данные

Повторение: Вариационный ряд, его характеристики : Ø Задача Имеются данные об успеваемости 20 студентов группы по теории статистики за сессию: 5, 3, 5, 5, 5, 4, 5, 2, 5, 3, 4, 2, 5, 3, 2, 5, 4, 4 5, 4 Постройте дискретный вариационный ряд, Рассчитайте основные статистические характеристики, Сделайте статистический анализ Стаж работы 22 рабочих бригады характеризуется следующими признаками: 2, 4, 5, 5, 6, 6, 7, 7, 8, 8, 9, 10, 11, 4, 3, 3, 4, 4, 5 Постройте интервальный вариационный ряд, Рассчитайте основные статистические характеристики, Сделайте статистический анализ

СРЕДНИЕ ВЕЛИЧИНЫ И ПОКАЗАТЕЛИ ВАРИАЦИИпозволяют судить о характерных особенностях вариационного ряда и называют СТАТИСТИЧЕСКИМИ ХАРАКТЕРИСТИКАМИ 1 Средние величины имеют туже размерность , что и признак 2 Вокруг средних величин концентрируются наблюдавшиеся значения признака 3 Виды средних величин: арифметическая, геометрическая, средняя квадратическая, средняя кубическая, 4 Вид средней арифметической выбирают в зависимости от того какое свойство вариационного ряда мы хотим представить 5 Наиболее распространена – средняя арифметическая.

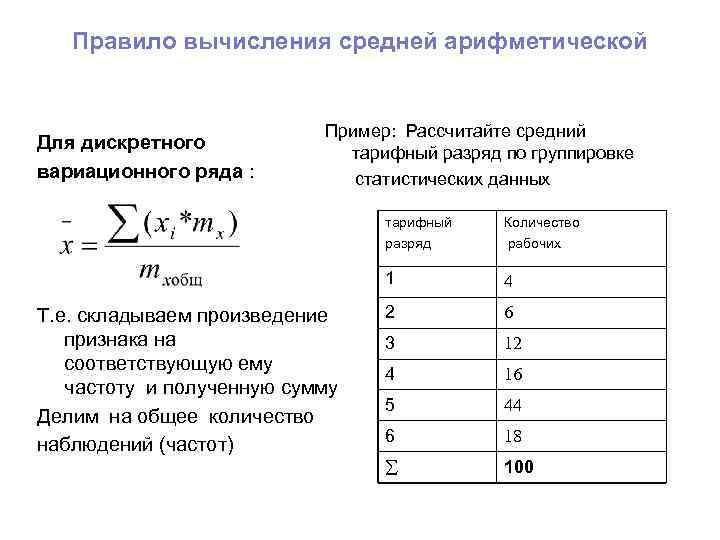Правило вычисления средней арифметической Для дискретного вариационного ряда : Пример: Рассчитайте средний тарифный разряд по группировке статистических данных тарифный разряд 1 Т. е. складываем произведение признака на соответствующую ему частоту и полученную сумму Делим на общее количество наблюдений (частот) Количество рабочих 4 2 6 3 12 4 16 5 44 6 18 100

Правило вычисления средней арифметической Пример: Рассчитайте средний тарифный разряд по группировке статистических данных Для интервального вариационного ряда Х=(5*88. 5+10*95. 5+…)/(5+10+ …) необходимо Определить среднюю для каждого интервала, затем – среднюю для всего ряда. Средняя для каждого интервала определяется как полусумма верхней и нижней границ Количество % выполнения предприятий плана 85 -92 5 93 -100 10 101 -108 30 109 -116 26 117 -123 13 124 -131 9 131 -138 9 138 -143 3 102

Структурные средние : МЕДИАНА И МОДА • Медиана – значение признака, приходящееся на середину ранжированного ряда, это значение признака, которыйделит ранжированный ряд на две равные по объему группы Задача На участка дороги 4 населенных пункта. Для проектирования Строительства автобусной остановки собраны данные о числе предполагаемых пассажиров из каждого пункта. Результаты обследования Км 2 3 5 8 Число Пассажиров 50 30 40 10 n=130=2*65 M=(X(65)+X(66)/2=(3+3)/2=3

Структурные средние : МЕДИАНА И МОДА • Модой- называется число признака, которое наблюдалось наибольшее число раз Мода используется в тех случаях когда нужно дать ответ на вопрос какой товар, услуга имеет наибольший спрос, каковы преобладающие в данный момент уровни производительности труда, себестоимости.

Ряды динамики • это значения статистических показателей, которые представлены в определенной хронологической последовательности. • Каждый динамический ряд содержит две составляющие: 1) показатели периодов времени (годы, кварталы, месяцы, дни или даты); 2) показатели, характеризующие исследуемый объект за временные периоды или на соответствующие даты, которые называют уровнями ряда. Например: Индекс инфляции в 1993 г. % к декабрю 1992 г. период январь Индекс 126 инфляции февраль март апрель май июнь 162 221 264 310 190

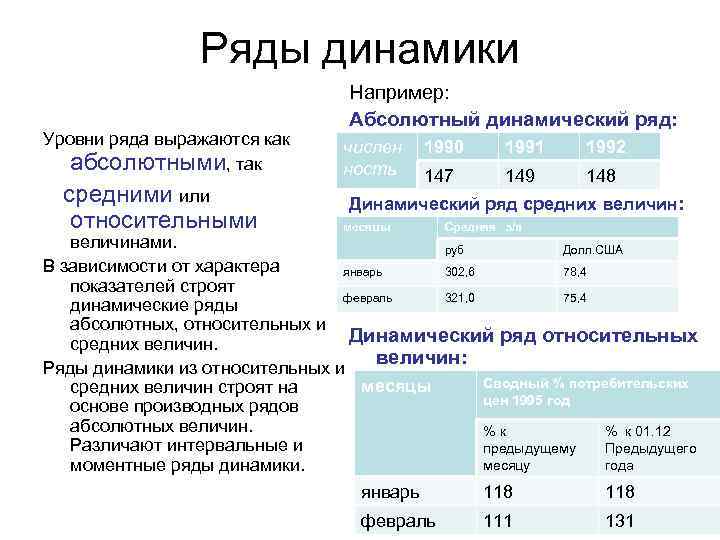Ряды динамики Уровни ряда выражаются как абсолютными, так средними или относительными Например: Абсолютный динамический ряд: числен ность 1990 1991 1992 147 149 148 Динамический ряд средних величин: месяцы Средняя з/п величинами. руб Долл. США В зависимости от характера январь 302, 6 78, 4 показателей строят февраль 321, 0 75, 4 динамические ряды абсолютных, относительных и Динамический ряд относительных средних величин: Ряды динамики из относительных и Сводный % потребительских месяцы средних величин строят на цен 1995 год основе производных рядов абсолютных величин. % к 01. 12 Различают интервальные и предыдущему Предыдущего месяцу года моментные ряды динамики. январь 118 февраль 111 131

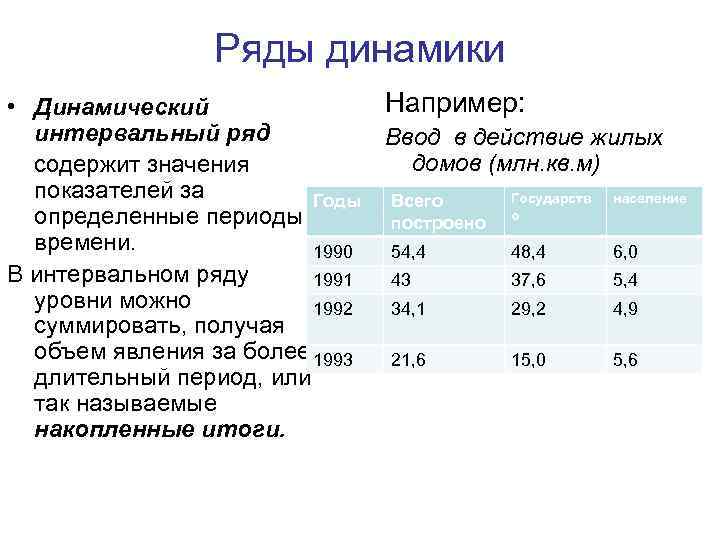Ряды динамики Например: • Динамический интервальный ряд Ввод в действие жилых домов (млн. кв. м) содержит значения показателей за Государств население Годы Всего определенные периоды построено о времени. 1990 54, 4 48, 4 6, 0 В интервальном ряду 1991 43 37, 6 5, 4 уровни можно 1992 34, 1 29, 2 4, 9 суммировать, получая объем явления за более 1993 21, 6 15, 0 5, 6 длительный период, или так называемые накопленные итоги.

Ряды динамики • Динамический моментный Например: ряд отражает значения показателей на Численность 1992 определенный момент населения времени (дату времени). • В моментных рядах 148, 3 исследователя может интересовать только разность явлений, отражающая изменение уровня ряда между определенными датами, поскольку сумма уровней здесь не имеет реального содержания. • Накопленные итоги здесь не рассчитываются 1993 1994 148, 3 148

Ряды динамики Важнейшим условием правильного построения динамических рядов является Сопоставимость уровней рядов, относящихся к различным периодам. Уровни должны быть представлены в однородных величинах, должна иметь место одинаковая полнота охвата различных частей явления.

Показатели анализа рядов динамики – Если в ходе исследования необходимо сравнить несколько последовательных уровней, то можно получить или сравнение с постоянной базой (базисные показатели), или сравнение с переменной базой (цепные показатели). • Базисные показатели характеризуют итоговый результат всех изменений в уровнях ряда от периода базисного уровня до данного (iго) периода. • Цепные показатели характеризуют интенсивность изменения уровня от одного периода к другому в пределах того промежутка времени, который исследуется.

Абсолютный прирост выражает абсолютную скорость изменения ряда динамики и определяется как разность между данным уровнем и уровнем, принятым за базу сравнения. Абсолютный прирост (базисный) • где yi - уровень сравниваемого периода; y 0 - уровень базисного периода. Абсолютный прирост с переменной базой (цепной), который называют скоростью роста, где yi - уровень сравниваемого периода; yi-1 - уровень предшествующего периода.

Коэффициент роста Ki определяется как отношение данного уровня к предыдущему или базисному, показывает относительную скорость изменения ряда. Если коэффициент роста выражается в процентах, то его называют темпом роста. • Коэффициент роста базисный Темп роста • Коэффициент роста цепной

Темп прироста ТП определяется как отношение абсолютного прироста данного уровня к предыдущему или базисному. • Темп прироста базисный • Темп прироста цепной

Индексы. В статистической практике индексный метод имеет такое же широкое распространение, как и метод средних величин. • НАЗНАЧЕНИЕ: • И – выступает как показатель Индексами называют динамики сравнительные • оценивает среднюю степень выполнения плана по совокупности в относительные величины, целом или по ее части которые характеризуют • И – выступает как показатель изменение сложных выполнения плана социально-экономических • устанавливает среднее соотношение показателей (показатели, сложных явлений в пространстве состоящие из • И – выступает , как показатель несуммируемых сравнения элементов) во времени, в • определяет роль отдельных факторов в пространстве, по сравнению общем изменении сложных явлений во времени с планом. • или в пространстве И –выступает , как аналитическое средство.

• По степени охвата различают индивидуальные и общие индексы. НАПРИМЕР: • Индивидуальные индексы выражают соотношение отдельных элементов совокупности. • Индивидуальный индекс обозначается i и определяется путем сопоставления • двух величин , характеризующих уровень изучаемого явления во времени или в пространстве ГОД 1990 ПРОИЗВЕДЕНО Млн. т. 55, 4 1998 80, 4 уровень- это год явление – производство i=80, 4/55, 4=1, 45 или на 45 % • 1, 45 – это и есть индивидуальный индекс , характеризующий динамику производства, который определяется путем сопоставления двух величин , характеризующих уровень изучаемого явления.

НАПРИМЕР: • • • • В статистической практике КОЛИЧЕСТВО принято обозначать буквой – q ГОД ПРОИЗВЕДЕНО Млн. т. 1990 55, 4 ТЕКУЩЙ ПЕРИОД – период 1998 80, 4 уровень , которого сравнивается В приведенном примере вычислен ( в примере это – • ИНДИВИДУАЛЬНЫЙ ИНДЕКС 1998 год), ФИЗИЧЕСКОГО ОБЪЕМА ПРОДУКЦИИ текущий период обозначается • iq=q 1/q 0 подстрочной буквой “ 1” , • q 1, q 0 – кол-во произведенной продукции в т. е. - q 1 отчетном и базисном году. БАЗИСНЫЙ ПЕРИОД – период с уровнем, которого проводится сравнение Базисный период обозначается подстрочной буквой « 0» , т. е q 0 • этот индекс характеризует изменение физического объема продукции во времени и сравнивает производство одного и того же вида продукции за один и тот же период

• • В статистической практике цену принято обозначать – р , • Цепные и базисные индексы себестоимость – z, затраты времени на • Базисные индексы – характеризуют производство единицы изменение явлений за длительный продукции – t период • ИНДЕКС ЦЕНПо отношению к какой-либо отправной • ip=p 1/p 0 точке(постоянная база сравнения). • ИНДЕКС СЕБЕСТОИМОСТИ • iz=z 1/z 0 • Цепные индексы- характеризуют • ИНДЕКС ТРУДОЕМКОСТИтекущие изменения (переменная база сравнения) • it=t 1/t 0 • ИНДИВИДУАЛЬНЫЕ ИНДЕКСЫ Взаимосвязь между базисными и ПРЕДСТАВЛЯЮТ СОБОЙ ПО СУЩЕСТВУ , цепными индексами: ОТНОСИТЕЛЬНЫЕ ВЕЛИЧИНЫ ДИНАМИКИ, ВЫПОЛНЕНИЯ ПЛАНА ИЛИ СРАНЕНИЯ. • ПРОИЗВЕДЕНИЕ ЦЕПНЫХ ИНДЕКСОВ РАВНО БАЗИСНОМУ.

ГОД ЦЕНА ПРОИЗВЕДЕНО за единицу Млн. т. продукции • В статистике часто приходится иметь дело с показателями связанными между собой , 1996 125 16, 7 как сомножители в 1997 141, 8 14, 1 произведении. • Например: 1998* 193 10, 9 • Валовой сбор – произведение урожайности и площади, *- с учетом деноминации • Фонд з/п- произведение средней Можно рассчитать товарооборот , з/п и численности работников который будет равен – р* q • Товарооборот- произведение • цены и физического объема Индивидуальный индекс товарооборота и ip*q=ip*iq т. д. • В ТАКОЙ ЖЕ СВЯЗИ НАХОДЯТСЯ И ИНДЕКСЫ ЭТИХ ПОКАЗАТЕЛЕЙ. • Рассчитаем индивидуальные индексы цен, физического объема, товарооборота. Проверить взаимосвязь цепных и базисных индексов.

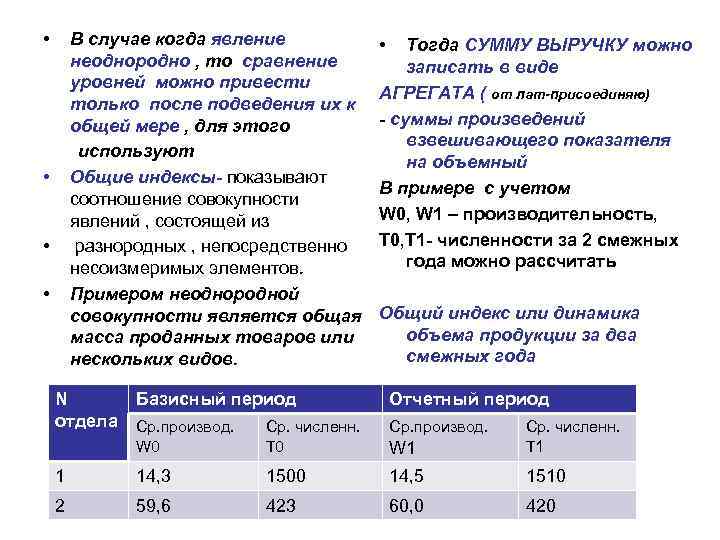• В случае когда явление неоднородно , то сравнение уровней можно привести только после подведения их к общей мере , для этого используют • Общие индексы- показывают соотношение совокупности явлений , состоящей из • разнородных , непосредственно несоизмеримых элементов. • Примером неоднородной совокупности является общая масса проданных товаров или нескольких видов. N Базисный период отдела Ср. производ. Ср. численн. • Тогда СУММУ ВЫРУЧКУ можно записать в виде АГРЕГАТА ( от лат-присоединяю) - суммы произведений взвешивающего показателя на объемный В примере с учетом W 0, W 1 – производительность, Т 0, Т 1 - численности за 2 смежных года можно рассчитать Общий индекс или динамика объема продукции за два смежных года Отчетный период Ср. производ. Ср. численн. T 1 W 1 W 0 T 0 1 14, 3 1500 14, 5 1510 2 59, 6 423 60, 0 420

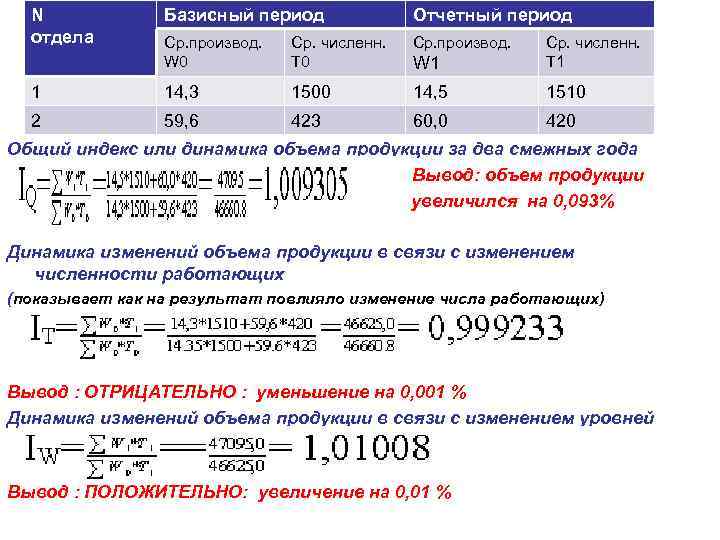N отдела Базисный период Отчетный период Ср. производ. W 0 Ср. численн. T 0 Ср. производ. W 1 Ср. численн. T 1 1 14, 3 1500 14, 5 1510 2 59, 6 423 60, 0 420 Общий индекс или динамика объема продукции за два смежных года Вывод: объем продукции увеличился на 0, 093% Динамика изменений объема продукции в связи с изменением численности работающих (показывает как на результат повлияло изменение числа работающих) Вывод : ОТРИЦАТЕЛЬНО : уменьшение на 0, 001 % Динамика изменений объема продукции в связи с изменением уровней производительности труда Вывод : ПОЛОЖИТЕЛЬНО: увеличение на 0, 01 %

ВЗАИМОСВЯЗЬ ОБЩИХ ИНДЕКСОВ Если индексы рассчитаны верны, то * Используем полученные индексы для анализа общего прироста продукции ΔQ ΔQ(T)= Q 0*(IT-1)= 46660. 8*(0. 9992331)=35. 8 тыс. руб. - прирост продукции в связи с изменением численности ΔQ(W)=Q 0*IT*(IW 1)= 46660. 8*0. 999233*(1. 01008 -1) = 470 тыс. руб. - прирост продукции в связи с изменением численности и выработки Вычисляем общий объема прирост продукции Q= ΔQ(T)+ ΔQ(W)= -35. 8 + 470 =434. 2 тыс. руб и делаем Общий экономический вывод

ВЫВОД : Экономического анализа статистических данных позволили выявить следующие результаты: 1. Общий прирост объема продукции составил Q= 434, 2 тыс. руб, что соотвествует динамике IQ= 1, 0099923 2. Динамика изменения прироста объема продукции объясняется - динамикой изменения численности (в IТ раз) IТ = 0, 999233 , что соответствует приросту продукции в связи с изменением численности ΔQ(T)= -35. 8 тыс. руб -динамикой изменением уровней производительности труда (в IW раз) IW= 1, 01008 что соответствует приросту продукции в связи с изменением уровня производительности труда ΔQ(W)= 470 тыс. руб.