Математика эпохи Возрождения Подготовили студенты 1 курса

«Математика эпохи Возрождения» Подготовили студенты 1 курса гр. 15101

Содержание Проблема решения алгебраических уравнений Алгебра Виета Проблема перспективы в живописи Ренессанса и математика Иррациональные числа Отрицательные, мнимые и комплексные числа Десятичные дроби Тригонометрия в астрономических сочинениях Список литературы

Проблема решения алгебраических уравнений, совершенствование символики, решение уравнений 3 -й и 4 -й степеней в радикалах Крупнейший европейский алгебраист XV в. -итальянец Лука Пачоли. Основной труд - «Сумма [знаний] по арифметике, геометрии, отношениям и пропорциональности» В арифметической части «Суммы» излагались различные приемы арифметических действий, в том числе индийский прием умножения с помощью решетки. Пачоли дает мистическое «объяснение» того, что совершенные числа оканчиваются лишь на 6 и 8 тем, что добрые и совершенные люди соблюдают установленный порядок.

Алгебраические символы Пачоли R*, (radice — корень) или R* 2 квадратный корень R* 3 или R* cuba кубический корень R* 4 или R*R* корень четвертой степени N (numero — число) Свободный член в уравнениях х — со (cosa — вещь) х2 — се (censo — квадрат, от латинского census) х3 — cu (cubo) x 4 — се. (censo de censo) x 8 — ce. ce. (censo de censo, de censo) x 9 — cu. (cubo de cubo) р˜ сложение m˜ вычитание

Во Франции оригинальный вклад в алгебру был сделан бакалавром медицины Никола Шюке Основной труд Шюке- «Наука о числах в трех частях» 1484 г. Сочинение содержит правила вычислений с рациональными числами, затем с иррациональными корнями и, наконец, учение об уравнениях. В нем по аналогии с итальянским термином millione (буквально «большая тысяча» ), вводятся дальнейшие термины «биллион» , «триллион» и т. д. до «нониллиона» . Сопоставил арифметическую и геометрическую прогрессии. Написав их друг под другом, он отмечает, что произведению двух членов нижней прогрессии соответствует сумма стоящих над ними членов верхней. Здесь налицо предвосхищение свойств будущих логарифмов. Так же как и Пачоли, Шюке приводит правила действий с отрицательными числами и пользуется для сложения и вычитания знаками р˜ и m˜. Знак m˜ служит и для обозначения отрицательных чисел

Следующий шаг был сделан немецкими алгебраистами XVI в. , известными под названием «коссистов» . (Coss — от итальянского слова cosa — вещь, неизвестная у итальянских алгебраистов) Ян Видман, немецкий математик, был первым, кто начал в университете чтение лекций по алгебре. Он ввел знаки + и —, заменившие знаки р˜ и m˜ итальянцев Также видными коссистами были Адам Ризе и Кристоф Рудольф

Кубическое уравнение вида: х3 + ах = b (а, b > 0) первому удалось решить профессору Болонского университета Ши-пионе дель Ферро. Позже Николо Тарталья нашел и решил уравнение вида: х3 = ах + b.

Луиджи Феррари, ученик Кардано, открыл метод решения уравнений четвертой степени: х4 + ах2 + bх + с = 0 Решение уравнений третьей и четвертой степеней в радикалах имело огромное значение для прогресса алгебры, да и всей математики.

Алгебра Виета • Франсуа Виет, французский математик, положил много сил для усовершенствования тригонометрии • Главный труд- «Введение в искусство анализа» • Замысел Виета определялся следующими соображениями: крупные успехи итальянских математиков в решении уравнений 3 -й и 4 -й степени опирались на высокую эффективность алгебраических приемов

Символика до Виета Все величины обозначены буквами: неизвестные — гласными, известные—согласными. Числа — безразмерны, положительны, рациональны; величины же имеют размерность Сложение и вычитание производятся над одноразмерными величинами. Умножение и деление вызывают изменение размерности и т. д.

Символика Виета тяжела, не всегда понятна, перемежается сокращенными и даже несокращенными словами Например: 1) A cubus+B planum in aequatur D solido ( A 3 +3 AB=D) 2) B parabolain A gradum−A potestate aequatur Z hom ogenae (B A n − A m+n =Z). Стало впервые возможным выражение уравнений, их свойств, общими формулами Объектами математических операций стали не числовые задачи, а сами алгебраические выражения.

При решении уравнений Виет разыскивает положительные корни. С помощью преобразования х = (-у) он подходит к проблеме нахождения отрицательных корней, высказывает ряд теорем о взаимозависимости корней уравнений и их коэффициентов, включающих частные случаи теоремы, известной ныне под его именем. В связи с этим он рассматривает, в указанных выше границах, образование уравнений произведением биномов: P n ( x )= ∏ k=1 n ( x− x k ) ( n<5 , x k<0 ).

Алгебра Виета была еще несовершенной и имела крупные недостатки: Ее очень утяжеляла видовая трактовка величин, обладающих размерностью. В ней нет общей трактовки степеней, все степени натуральные. Принципиальное разделение чисел и алгебраических величин не позволяло ему употреблять радикалы для величин, а лишь для чисел и т. п.

Проблема перспективы в живописи Ренессанса и математика «Оптика» Евклида «Оптическая часть астрономии» Кеплера «Планисферия» Птолемея Виды центральных проекций рассматривались в следующих трудах: «Книга оптики» Ибн ал-Хайсама «Оптика» Витело

Леон-Баттисты Альберти в своем трактате « О живописи» разработал метод построения изображения расположенных друг за другом равных и параллельных отрезков в виде параллельных отрезков, заключенных между двумя линиями, пересекающимися на линии горизонта.

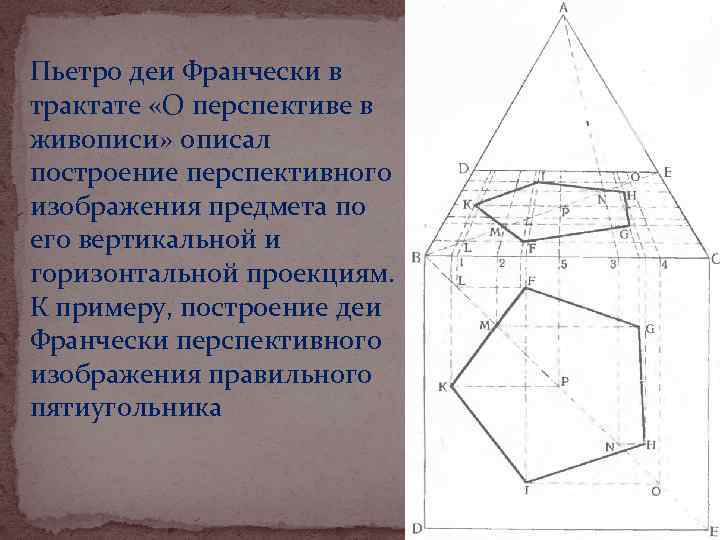Пьетро деи Франчески в трактате «О перспективе в живописи» описал построение перспективного изображения предмета по его вертикальной и горизонтальной проекциям. К примеру, построение деи Франчески перспективного изображения правильного пятиугольника

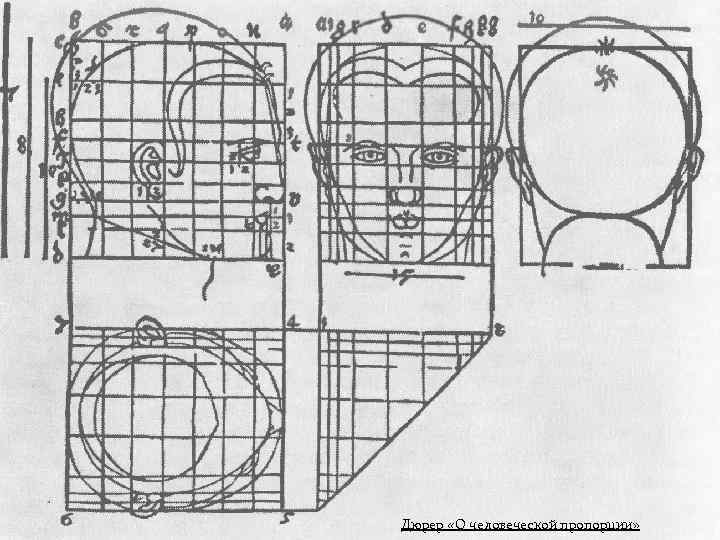Дюрер «О человеческой пропорции»

Иррациональные числа Арифметические действия с квадратичными иррациональностями встречаются в следующих трудах: сочинения Кардано «Сумма» Луки Пачоли «Общий трактат» Тартальи

Подробно этой теорией занимались: Кристоф Рудольф «Алгебра» Михаэль Штифель «Полная арифметика»

Противоположную позицию занял Симон Стевин. . Он полагал, что • Число является непрерывным количеством • нет никаких абсурдных, иррациональных, неправильных, невыразимых или глухих чисел Эта концепция единого понятия действительного числа имела важнейшее значение для дальнейших, успехов алгебры и ее приложений в геометрии, приведших к появлению

Отрицательные, мнимые и комплексные числа Впервые отрицательные числа появились в Европе в «Книге абака» Леонардо Пизанского Также отрицательные числа имеются и в арифметиках Пачоли и Шюке Однако Кардано называет отрицательные корни алгебраических уравнений «фиктивными»

Вслед за тем Бомбелли сообщает восемь правил умножения мнимых и действительных чисел, закладывая тем самым первый камень фундамента теории комплексных чисел. В наших обозначепиях: (± 1)i=±i, (± 1)(−i)=∓i, (+i)=− 1 , (+i)(−i)=+ 1 , (−i)(+i)=+ 1 (−i)=+1. Бомбелли был последним в блестящей плеяде итальянских алгебраистов XVI в.

Единая трактовка различных форм квадратных уравнений, в Европе впервые встречается в «Полной арифметике» М. Штифеля, который записывает все три вида этих уравнений в форме, равносильной современной записи 2 = ax + b x и описывает решение этого уравнения во всех трех случаях (а > 0, b > 0; а > 0, b < 0 и а < 0, b > 0).

положительные и отрицательные числа стали рассматриваться как координаты точек Термины «положительпый» , «отрицательный» впервые в Европе появились в рукописи «Initius Algebra» . Впервые мнимые величины встречаются в «Великом искусстве» Кардано Первым математиком, оценившим пользу мнимых величин, в частности при решении кубического уравнения в «неприводимом» случае, был работавший в Болонье инженер-гидравлик Рафаэль Бомбелли

Десятичные дроби В средневековой Европе, как и в странах ислама, широко применялись шестидесятиричные дроби. , которые применялись в астрономических вычислениях и таблицах, поэтому нередко они назывались астрономическими; иногда их называли также физическими или философскими Георг Пейербах в своих неопубликованных таблицах синусов соединил шестидесятиричный и десятичный принципы: он выразил значения синусов в целых десятичных числах при радиусе круга Примеру Пейербаха последовал сначала его ученик Иоганн Мюллер, но затем он отказался от шестидесятиричности и в 1467 г. составил первые чисто десятичные тригонометрические таблицы — таблицы тангенсов при радиусе 105, посмертно изданные в Аугсбурге в 1490 г.

Ф. Виет, французского математик XVI в. , в своем труде «Математический канон выступил в пользу употребления, как он выражался, тысячных и тысяч, сотых и сотен, десятых и десятков и т. д. взамен шестидесятиричной системы целых и дробей. При записи десятичных дробей Виет не придерживался какого-либо одного обозначения. Нередко он пишет как числитель, так и знаменатель, иногда отделяет цифры целой части от дробной вертикальной чертой синус 60° при r = 100 000 есть 86, 602| 540, 37

Широкое распространение десятичных дробей в Европе началось только после выхода в свет «Десятой» фламандского математика Симона Стевина. он с большим пылом агитирует как за повсеместное введение десятичных дробей, так и за введение десятичной системы мер и монет. Стевин обозначает целые знаком 0, десятые — знаком 1, сотые — знаком 2 и т. д. , причем цифры 0, 1, 2, . . . стоят над значащими цифрами или после них в кружках. Громоздкая символика Стевина нашла мало сторонников. Еще при его жизни Ф. Виет ввел специальные знаки для произвольных коэффициентов алгебраических выражений.

Тригонометрия в астрономических сочинениях Тригонометрия в Европе появляется в XII в. вместе с переводами астрономических сочинений ученых стран ислама С тригонометрией были тесно связаны исследования немецкого ученого-гуманиста Николая Кузанского Первым крупным сочинением по тригонометрии в Европе были «Пять книг о треугольниках всех видов» немецкого математика и астронома Иоганна Мюллера На развитие тригонометрии существенное влияние оказал великий польский астроном Николай Коперник

Открытия Коперника Вычислил точные таблицы синусов дал оригинальный вывод теорем сферической тригонометрии он доказывает теорему синусов для прямоугольного сферического треугольника Термин «тень» был заменен на «тангенс» (от латинского слова tangens — «касающийся» ) в XVI в.

Общие выводы введена позиционная десятичная арифметика создана арифметическая и алгебраическая символика, отсутствие которой тормозило прогресс теории уравнений ранее Введены были дробные и отрицательные показатели и отрицательные числа успешно решена проблема решения в радикалах уравнений третьей и четвертой степеней Введение специальных буквенных обозначений для неизвестных и для коэффициентов многочленов, а также расширение символики алгебраических операций введены десятичные дроби созданы условия для возникновения теории переменных величин, символической алгебры, аналитической геометрии, дифференциального и интегрального исчислений.

Список литературы http: //www. math. asu. ru Рыбников, К. А. «История математики»