Математика Древней Греции История VI в

Математика Древней Греции

История • VI в. до н. э. «Они первые и единственные в то время изгнали бывших у них царей и установили у себя демократию, полагая, что свобода всех производит величайшее единодушие… Властвовать друг над другом путем насилия, думали они, свойственно диким зверям, а люди должны законом определить справедливое, словом убедить, делом повиноваться тому и другому ; закон должен быть царем, слово – наставником» . (Лисий, афинский оратор)

История • V – начало IV в. до н. э. Золотой век Афин, которые становятся политическим и культурным центром Греции. Создание Академии Платона (ок. 388 г. до н. э. ) и Ликея Аристотеля (335 г. до н. э. ) – прообраза будущих университетов. • 337 г. до н. э. Завоевание материковой Греции Филиппом, правителем Македонии (отцом Александра Македонского).

Греческая наука • В VI в. до н. э. были построены не только первые математические теории, но и первые математические модели мира. Ученые пришли к мысли, что математика является универсальным языком для выражения законов природы. • Теория строилась исходя из конечного числа посылок, а ее положения выводились из них с помощью цепочки логических умозаключений или эффективных конструкций. • Основным методом установления истины и исследования связи между предложениями становится логическое доказательство.

Греческая наука • VI в. до н. э. был временем знаменитых натурфилософских школ: ионийской и пифагорейской. • Начало греческой науки положила ионийская школа, основателем которой был Фалес – купец, политический деятель, философ, астроном и математик, живший в Милете – богатой греческой колонии в Малой Азии. Ионийцы первыми среди эллинов занялись геометрий.

Фалес Милетский • Доказал, что диаметр делит круг пополам. • Доказал предложение о равенстве углов при основании равнобедренного треугольника. • Открыл, что при пересечении двух прямых получаются равные углы. • Доказал теорему о равенстве двух треугольников, имеющих равными сторону и два угла. • Ввел понятие движения, в частности, поворота. К ионийской школе принадлежали также ученики Фалеса – Анаксимен и Анаксимандр.

Пифагор (ок. 580 – 497 гг. до н. э. ) • Родился на греческом острове Самос. • Изучал математику в Милете, Египте, Вавилоне. • Примерно в 540 г. до н. э. переехал в Кротон (Южная Италия), где основал знаменитый пифагорейский союз. • Ввел в обиход понятие «философия» (философос – любящий мудрость).

Школа Пифагора • Девиз школы: «Все есть число» . • Пифагорейцы занимались астрономией, геометрией, гармонией (теорией музыки) и арифметикой (теорией чисел). • Говорят, что само слово математика ( «то, что изучается» было изобретено пифагорейцами. • Математические результаты считались собственностью школы, и их первооткрывателей чужакам не называли.

Школа Пифагора Обучение начиналось с акусм – символических фраз, над которыми ученик должен был размышлять, чтобы понять их смысл: • Через весы не переступай (т. е. избегай алчности). • Огня ножом не вороши (т. е. человека гневного резкими словами не задевай). • Не ешь сердца (т. е. не удручай себя горем). • Не садись на хлебную меру (т. е. не живи праздно). • По торной дороге не ходи (т. е. следуй не мнению толпы, а мнению немногих понимающих). • Переходя границу, не оборачивайся. • Ношу помогай не взваливать, а сваливать. • Постель держи свернутой. • Руку без разбора не подавай.

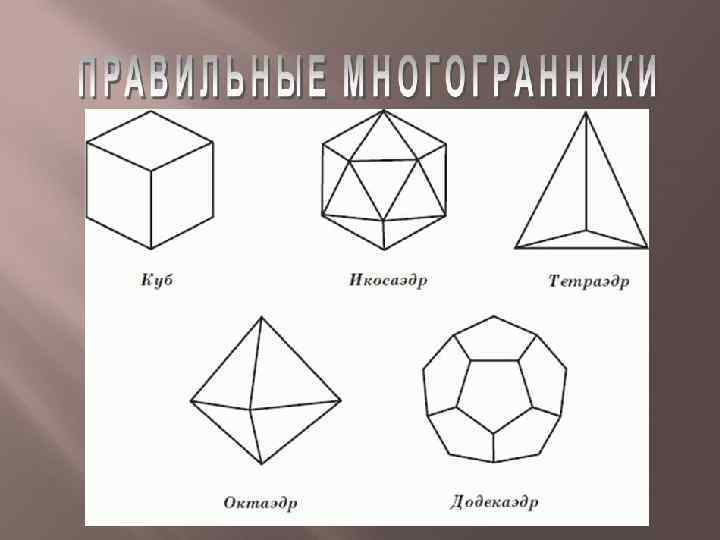
Достижения в геометрии • Пифагорейцы развили и обосновали планиметрию прямолинейных фигур: учение о параллельных линиях, треугольниках, четырехугольниках, правильных многоугольниках. Получила развитие элементарная теория окружности и круга. • Венчало их систему доказательство знаменитой «теоремы Пифагора» , которая до этого была известна только для частных случаев. • Пифагорейцы знали три из пяти правильных многогранников (тетраэдр, куб, октаэдр).

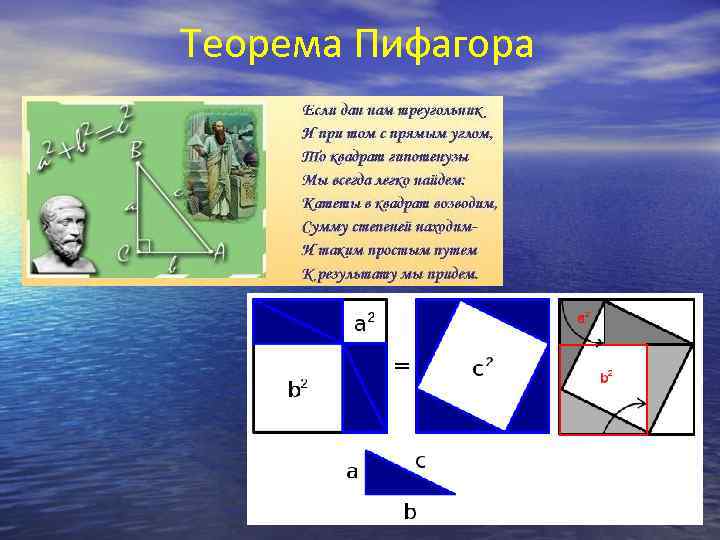Теорема Пифагора

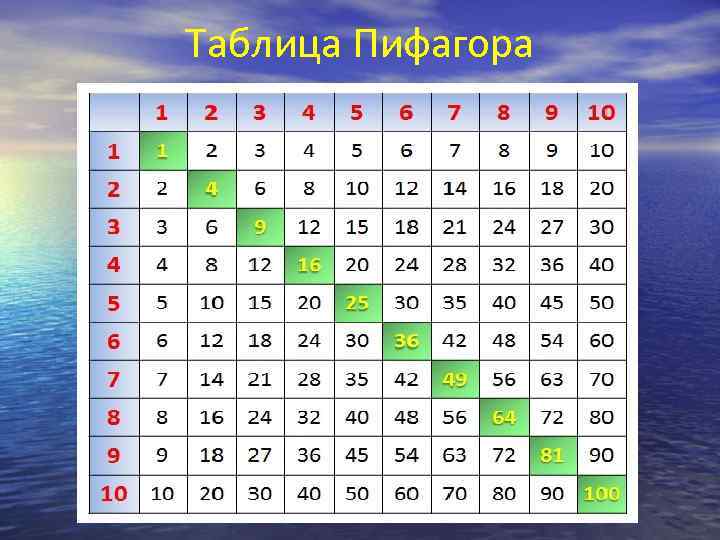Таблица Пифагора

Арифметика целых чисел • Изучая свойства чисел, пифагорейцы впервые обратили внимание на законы их делимости. Они разбили все числа на четные и нечетные, а также на простые и составные. • Пифагорейцы открыли совершенные числа, т. е. такие, которые равны сумме своих делителей (исключая само число). 6 = 1+2+3 28 = 1+2+4+7+14 • В Греции начали оперировать с дробями вида m/n. Сложение и вычитание производилось путем приведения к общему знаменателю, дроби умели сокращать, умножать и делить.

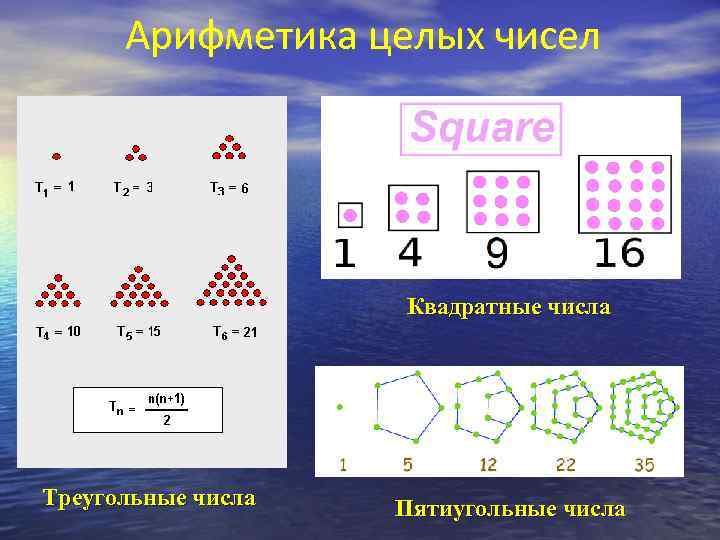Арифметика целых чисел Квадратные числа Треугольные числа Пятиугольные числа

Открытие несоизмеримых величин Это открытие явилось поворотным пунктом в развитии математики. Оно означало, что целых и рациональных чисел недостаточно для выражения отношения любых двух отрезков. Аристотель писал, что если допустить соизмеримость диагонали и стороны квадрата, то четное число бы равно нечетному. Из этой фразы ясно, что доказательство проводилось методом от противного. Открытие несоизмеримых отрезков ознаменовало начало кризиса пифагорейской философии.

Значение школы Пифагора Главной заслугой пифагорейцев в области науки является существенное развитие математики как по содержанию, так и по форме. По содержанию - открытие новых математических фактов. По форме - построение геометрии и арифметики как теоретических, доказательных наук, изучающих свойства отвлеченных понятий о числах и геометрических формах.

Магия чисел «Числа правят миром»

Магия чисел «Математика – язык науки!»

Магия чисел «Природа разговаривает с нами на языке математики»

Проблема бесконечности Понятие бесконечности как математическая категория впервые появляется у Анаксагора (около 500 - 428 гг. до н. э). В сочинении “О природе" Анаксагор писал: вещи бесконечно делимы, нет последней ступени делимости материи; с другой стороны, всегда имеется нечто, что является большим.

Проблема бесконечности Понятие бесконечности подвергалось серьезной критике со стороны Зенона Элейского (ок. 490 -430 гг. до н. э. ). Зенон был учеником Парменида, главы элейской школы. Парменид утверждал, что бытие едино, неподвижно и неизменно. Движение, изменение - это только видимость, обусловленная несовершенством наших органов чувств. Мир (бытие) может быть познан только разумом, но не чувствами.

Период наивысшего расцвета • В деятельности Евклида, Аполлония Пергского и особенно Архимеда период самостоятельной деятельности греков в области математики достиг момента наибольшей высоты математических исследований как в количественном, так и в качественном отношении.

Евклид. «Начала» Главный труд Евклида, написанный около 300 г. До н. э. и посвящённый систематическому построению геометрии. «Начала» — вершина античной геометрии и античной математики вообще, итог её 300 летнего развития и основа для последующих исследований. «Начала» — древнейшее из дошедших до нас античных математических сочинений. Все труды предшественников Евклида известны нам только по упоминаниям и цитатам позднейших комментаторов.

«Начала» Евклида

Из других сочинений по математике надо отметить «О делении фигур» , сохранившееся в арабском переводе, 4 книги «Конические сечения» , материал которых вошёл в произведение того же названия Аполлония Пергского, а также «Поризмы» , представление о которых можно получить из «Математического собрания» Паппа Александрийского.

Архимед родился в Сиракузах, греческой колонии на острове Сицилия. Отцом Архимеда был математик и астроном Фидий, состоявший, как утверждает Плутарх, в близком родстве с Гиероном II, тираном Сиракуз. Отец привил сыну с детства любовь к математике, механике и астрономии. Для обучения Архимед отправился в Александрию Египетскую — научный и культурный центр того времени.

Работы Архимеда относились почти ко всем областям математики того времени: ему принадлежат замечательные исследования по геометрии, арифметике, алгебре. Так, он нашёл все полуправильные многогранники, которые теперь носят его имя, значительно развил учение о конических сечениях, дал геометрический способ решения кубических уравнений вида x² (a ± x) = b, корни которых он находил с помощью пересечения параболы и гиперболы.

Архимед Однако главные математические достижения Архимеда касаются проблем, которые сейчас относят к области математического анализа. Греки до Архимеда сумели определить площади многогранников и круга, объём призмы и цилиндра, пирамиды и конуса. Но только Архимед нашёл гораздо более общий метод вычисления площадей или объёмов; для этого он усовершенствовал и виртуозно применял метод исчерпывания Евдокса Книдского. В своей работе «Послание к Эратосфену о методе» (иногда называемой «Метод механических теорем» ) он использовал бесконечно малые для вычисления объёмов. Идеи Архимеда легли впоследствии в основу интегрального исчисления.

Архимед Огромное значение для развития математики имело вычисленное Архимедом отношение длины окружности к диаметру. В работе «Об измерении круга» Архимед дал своё знаменитое приближения для числа π: «архимедово число» 22/7. Более того, он сумел оценить точность этого приближения: 223/71 < π < 22/7 посредством построения для круга вписанного и описанного 96 -угольников и вычисления длин их сторон.

Заключение Невозможно представить пути развития современной математики без фундаментальных основ и идей античной математики. Именно Греции мы обязаны возникновением математики как самостоятельной науки с присущими ей методами нахождения и установления истины, а также тем, что законы природы постижимы для человеческого разума, и математические модели — ключ к их познанию.