Математика 5 класс 1 Со склада было

Математика 5 класс

1. Со склада было отправлено 8 грузовиков, в каждом из которых было по 3 тонны груза. Каждая тонна груза состояла из 42 ящиков. Сколько всего ящиков было отправлено со склада? 2. Саше 12 лет, его сестре Ире 3 года, а их папе 36 лет. Во сколько раз Ира моложе папы и во сколько раз папа старше Саши? 3. Ученик прочел 81 страницу, ему осталось прочесть в 3 раза меньше, чем он уже прочел. Сколько всего страниц должен прочесть ученик? 4. Мотоциклист от пункта A до пункта B проехал 148 км. Для того чтобы добраться из пункта B в пункт C он должен преодолеть расстояние, которое в 4 раза меньше, чем он уже проехал. Сколько всего должен проехать мотоциклист? 5. От числа 540 отняли 480. Во сколько раз уменьшилось число 540? 6. В 14 ящиках 168 кг помидор. Сколько килограмм помидор в 18 таких ящиках?

ответы 1. 1008 ящиков. 2. Ира моложе папы в 12 раз, папа старше Саши в 3 раза. 3. 108 страниц 4. 185 км. 5. число 540 уменьшилось в 9 раз. 6. в 18 ящиках 216 кг помидор

Умножение и деление натуральных чисел

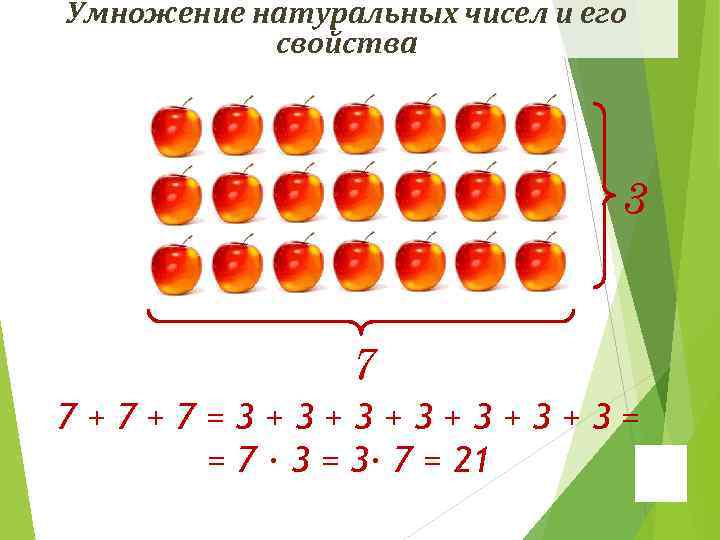
Умножение натуральных чисел и его свойства 3 7 7+7+7=3+3+3+3= = 7 ∙ 3 = 3· 7 = 21

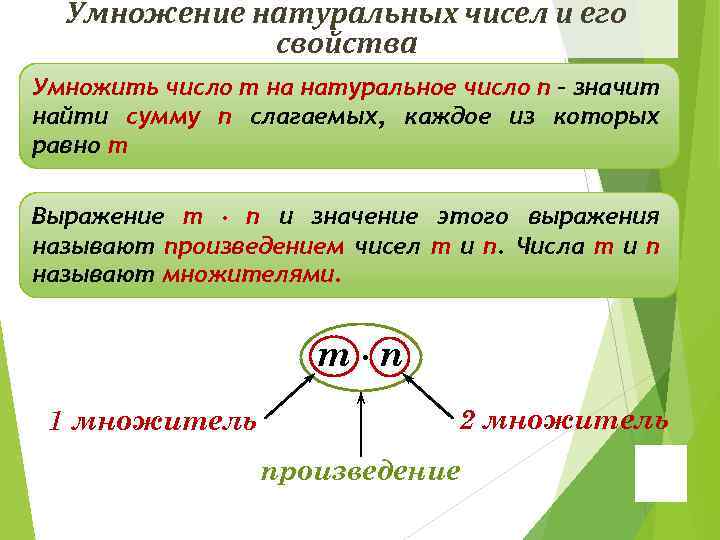
Умножение натуральных чисел и его свойства Умножить число m на натуральное число n – значит найти сумму n слагаемых, каждое из которых равно m Выражение m ∙ n и значение этого выражения называют произведением чисел m и n. Числа m и n называют множителями. m∙n 1 множитель 2 множитель произведение

Умножение натуральных чисел и его свойства 1. Переместительное свойство умножения: а∙b=b∙a 2. Сочетательное свойство умножения: а ∙ (b ∙ с) = (a ∙ b) ∙ с 3. Свойство умножения на единицу: а∙ 1=1∙а=а 4. Свойство умножения на ноль: а∙ 0=0∙а=0

Умножение натуральных чисел и его свойства 1 + … + 1 = 1· п = п п 0 + … + 0 = 0· п = 0 п (a + b) + … + (a + b) = п (a + b)· п

Умножение натуральных чисел и его свойства 8· х = 8 х a· b = ab 2· (a + b) = 2(a + b) (x + 2)· (y + 3) = (x + 2)(y + 3) (ab)c = abc Когда в записи произведения нет скобок, умножение выполняют по порядку слева направо.

Ответьте на вопросы: 1. Что значит умножить одно натуральное число на другое? 2. Как называют числа, которые перемножают? 3. Как называют результат умножения? 4. Чему равно 1· n? Чему равно 0· n? 5. Сформулируйте переместительное свойство умножения. Запишите его с помощью букв. 6. Сформулируйте сочетательное свойство умножения. Запишите его с помощью букв. 7. В каких случаях можно опустить знак умножения? 8. Чему равно произведение т· 1? 9. Чему равно произведение т· 0?

Тест 1. Равенство m ∙ (n ∙ k) = (m ∙ n) ∙ k является: а) переместительным свойством умножения; б) сочетательным свойством умножения; в) другим каким-то свойством умножения. 2. Равенство 49 ∙ 0 = 0 при помощи букв записывается: а) b ∙ 0 = 0; б) 0 ∙ b = b; в) b ∙ 49 = 49. 3. Произведение чисел 4 ∙ 222 ∙ 5 равно: а) 8885; б) 4445; в) 4440. 4. Запишите с помощью букв переместительное свойство умножения: а) a + b = b + a; б) a ∙ b = b ∙ a; в) a ∙ 0 = 0 ∙ a

Запомни: 5 · 2 = 10 25 ∙ 4 = 100 50 ∙ 2 = 100 125 ∙ 8 = 1000 250 ∙ 4 = 1000 500 ∙ 2 = 1000

Расшифруйте ребус: , Понедельник Вторник Среда Четверг Пятница Суббота Воскресенье 3, 4, 5, 2, 1 ИЕ

Упрощение выражений

Распределительное свойство умножения относительно сложения Для того чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить получившиеся произведения. (а + b)с = aс + bс Примеры: 3 a + 7 a = (3 + 7)a = 10 a 12 x + 6 x + 8 x = (12 + 6 + 8)x = 26 x 11 m + 9 m + 4 m + 5 = (11 + 9 + 4)m + 5 = 24 m + 5

Распределительное свойство умножения относительно вычитания Для того чтобы умножить разность на число, можно умножить на это число уменьшаемое и вычитаемое и из первого произведения вычесть второе. (а − b)с = aс − bс Примеры: 26 x − 12 x = (26 − 12)x = 14 x 15 a – 8 a – 2 a = (15 – 8 – 2)a = 5 a 31 m – 16 m – 4 m – 5 = (31 – 16 – 4)m – 5 = 11 m – 5

Решить уравнение: 3 у + 7 у + 25 = 85 (3 + 7)у + 25 = 85 10 у = 85 – 25 10 у = 60 : 10 у=6 3· 6 + 7· 6 + 25 = 85 85 = 85 Ответ: 6.

Тест 1. В одном мешке было х кг картофеля, а в другом в 2 раза больше. Сколько килограммов картофеля было в двух мешках? а) х; б) 3 х; в) 2 х; г) 4 х. 2. Вася решил а задач, а Миша – на 4 задачи больше. Сколько задач решили Вася и Миша вместе? а) 4 а; б) 6 а; в) 2 а + 4; г) а + 4. 3. Даны два выражения: 9 (856 + 342) и 9 ∙ 856 + 8 ∙ 342. Какое выражение больше? а) равны; б) первое; в) второе. 4. Упростите выражение: 20 · а · 25 · b. а) 50 аb; б) 500 а; в) 5000 аb; г) 500 ab.

Порядок выполнения действий

Порядок выполнения действий Сложение и вычитание чисел называют действиями первой ступени, а умножение и деление чисел – действиями второй ступени. Порядок выполнения действий при нахождении значений выражений определяется следующими правилами: 1. Если в выражении нет скобок и оно содержит действия только одной ступени, то их выполняют по порядку слева направо. 2. Если выражение содержит действия первой и второй ступени и в нем нет скобок, то сначала выполняют действия второй ступени, потом – действия первой ступени. 3. Если в выражении есть скобки, то сначала выполняют действия в скобках (учитывая при этом правила 1 и 2).

Примеры: 1 2 3 4 800 − 625 + 331 + 87 – 119 = 474 1 2 3 4 780 : 39 ∙ 212 : 106 ∙ 13 = 4 1 2 5 520 3 5781 − 28 ∙ 75 : 25 + 156 : 12 = 5710 3 2 1 5 4 36000 : (62 + 14 ∙ 2) – 23 ∙ 5 = 285

Порядок выполнения действий В выражениях, содержащих скобки, можно эти скобки не писать, если при этом порядок действий не изменяется: (53 – 12) + 14 = 53 – 12 + 14 (64 : 16) ∙ 25 = 64 : 16 ∙ 25 Изменять порядок действий можно на основе свойств сложения, вычитания и умножения.

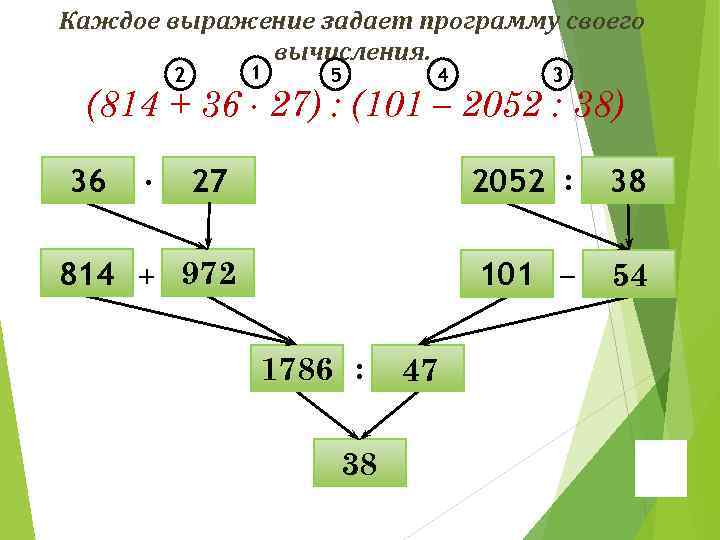
Каждое выражение задает программу своего вычисления. 1 2 5 4 3 (814 + 36 ∙ 27) : (101 – 2052 : 38) 27 2052 : 38 814 + 972 101 − 54 36 ∙ 1786 : 38 47

Ответьте на вопросы: 1. Какие действия относятся к действиям первой ступени и какие – к действиям второй ступени? 2. В каком порядке выполняют действия в выражениях без скобок, если в него входят действия одной и той же ступени; все арифметические действия? 3. В каком порядке выполняют действия в выражениях со скобками?