21236db141afd5f16b49ab1ce807c98a.ppt
- Количество слайдов: 91

Математична скарбничка 5 клас математика Укладач : Хеленюк Світлана Пилипівна , вчитель математики Ізяславського НРЦ Хмельницької обласної ради 1

Міністерство освіти та науки, молоді та спорту України Хмельницький обласний інститут післядипломної педагогічної освіти Ізяславський НРЦ Хмельницької обласної ради Хеленюк Світлана Пилипівна Електронний посібник з математики 5 клас «Математична скарбничка» Ізяслав – 2017 2

Хеленюк С. П. . Електронний посібник з математики для учнів 5 класу «Математична скарбничка» . Ізяслав 2017 Рецензенти: Хеленюк Ю. А. , директор Ізяславського навчально реабілітаційного центру. Остапчук О. Л. , вчитель історії і правознавства, заступник директора по навчальній роботі Ізяславського НРЦ. Електронний посібник складено відповідно до чинної програми для 5 -9 (10) класів спеціальних загальноосвітніх навчальних закладів для дітей з порушенням опорно-рухового апарату. Посібник містить основні означення, правила, властивості , формули для обчислення периметра і площі геометричних фігур. Наочна форма викладення матеріалу допоможе у вивченні нового матеріалу , в узагальненні знань з математики , дозволить скоротити час на повторення вивченого. Рекомендовано вчителям математики всіх типів навчальних закладів з метою надання допомоги у підготовці і проведенні уроків математики у 5 класі. 3

Зміст 1. Електронний посібник 2. 1 Титульна сторінка………………………………………. 2 2. 2 Пояснювальна записка…………………………………… 5 2. 3 Натуральні числа і дії з ними …………………. . . 7 2. 4 Рівняння ……………………………………………. 16 2. 5 Пряма. Промінь. Відрізок ………………………………. . 18 2. 6 Геометричні фігури …………………………………… 22 2. 7 Множення і ділення натуральних чисел …………………… 44 2. 8 Звичайні дроби …………………. . . 51 2. 6 Десяткові дроби ………………………………………. . 65 2. 7 Відсотки. ……………………………. . 83 2. Список використаних джерел …………………………………. . . 92 4

Пояснювальна записка Електронний посібник складено відповідно до чинної програми для 5 -9 (10) класів спеціальних загальноосвітніх навчальних закладів для дітей з порушенням опорно-рухового апарату. Посібник містить основні означення, правила, властивості , формули для обчислення периметра і площі геометричних фігур. Наочна форма викладення матеріалу допоможе у вивченні нового матеріалу , в узагальненні знань з математики , дозволить скоротити час на повторення вивченого. Зміст презентацій дозволяє використовувати посібник як і при вивченні навчального матеріалу так і при повторенні та систематизації вивченого матеріалу у 5 класі. Рекомендовано вчителям математики всіх типів навчальних закладів з метою надання допомоги у підготовці і проведенні уроків математики у 5 класі. 5

Математика. . . Наук цариця недосяжна, Могутня, щедра і прекрасна, Блискуче розум розвиває, І вірно мислити навчає. Неперевершена її краса, Чудова логіка струнка! 6

Натуральні числа та дії над ними. 7
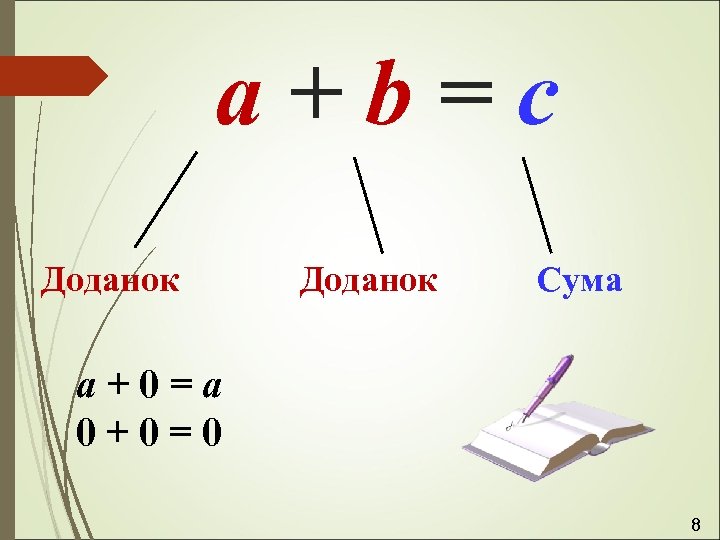
a+b=c Доданок Сума а+0=а 0+0=0 8
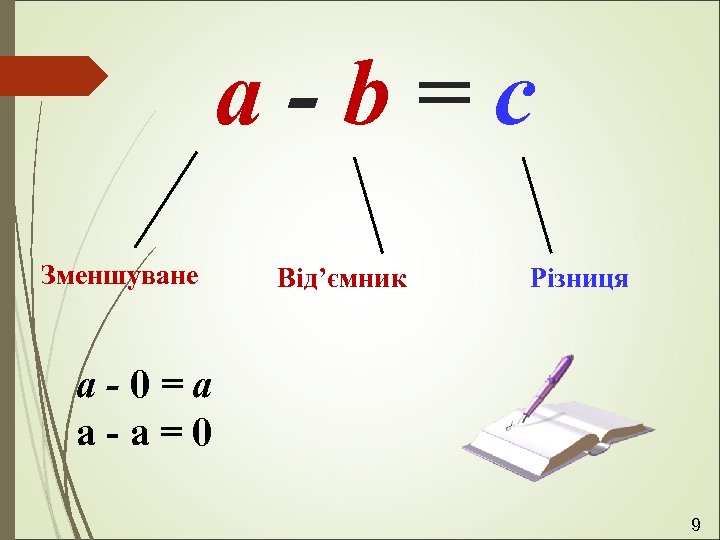
a-b=c Зменшуване Від’ємник Різниця а-0=а а-а=0 9

Властивості додавання: Переставна : а+в=в+а Сполучна : (а + в) + с = а + (в + с) 10

3853164 +2 7 0 0 5 0 3 6553667 11

3853164 -2 7 0 0 5 0 3 1152661 12

1)+3 км 948 м 4 км 76 м 7 км 1024 м 8 км 24 м 2)+3 948 м 4 076 м 8 км 24 м 13

Міри довжини 1 сажень ═ 3 аршинам (213 см); 1 верста ═ 500 сажням (1 км 67 м); 16 вершків ═ 28 дюймам (71 см); 1 фут ═ 12 дюймам (30 см 5 мм). 14

Розв'язування задач на рух. - відстань - швидкість - час руху 15

Рівняння Розв’язати рівняння – означає знайти всі його корені , або переконатися , що їх немає. Коренем рівняння називається число. яке при підстановці його замість букви перетворює рівняння на правильну числову рівність. 16

1. Щоб знайти невідомий доданок , треба від суми відняти відомий доданок. 2. Щоб знайти невідоме зменшуване, треба до різниці додати від’ємник. 3. Щоб знайти невідомий від’ємник , треба від зменшуваного відняти різницю. 17

Пряма. Промінь. Відрізок. 18

Завдання 1. Відмітьте дві точки А і В в зошиті. А В 2. Сполучить ці точки. 3. Що утворилося при цьому? 4. Продовжимо вліво і вправо пряму лінію 5. Що утворилося при цьому? 19
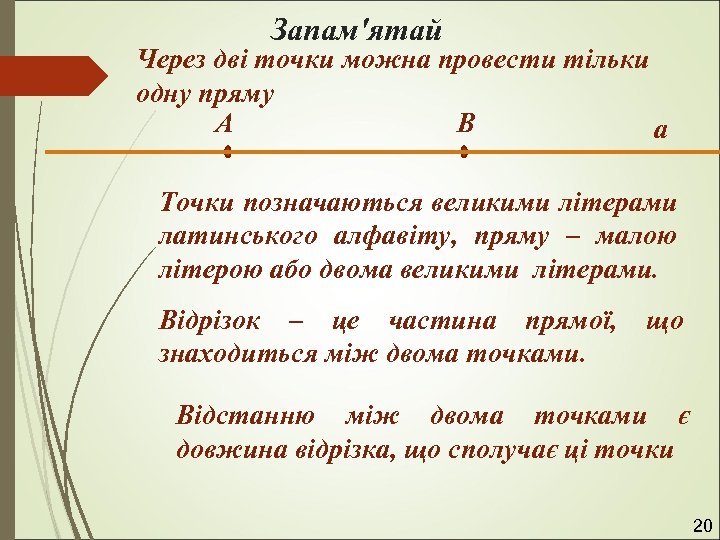
Запам'ятай Через дві точки можна провести тільки одну пряму А В а Точки позначаються великими літерами латинського алфавіту, пряму – малою літерою або двома великими літерами. Відрізок – це частина прямої, знаходиться між двома точками. що Відстанню між двома точками є довжина відрізка, що сполучає ці точки 20

Промінь Накреслимо відрізок CD C D Продовжимо відрізок вправо. Фігура, що утворилася при цьому, називається променем. Промінь – це частина прямої, що має початок, але не має кінця. 21
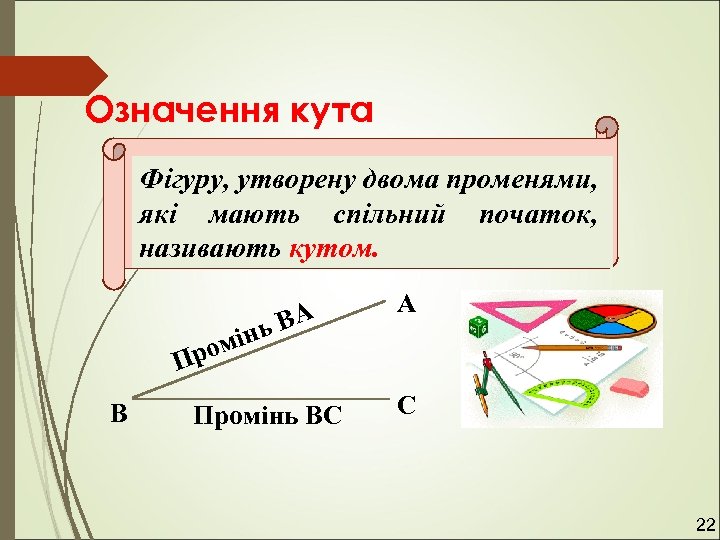
Означення кута Фігуру, утворену двома променями, які мають спільний початок, називають кутом. інь ом ВА А Пр В Промінь ВС С 22
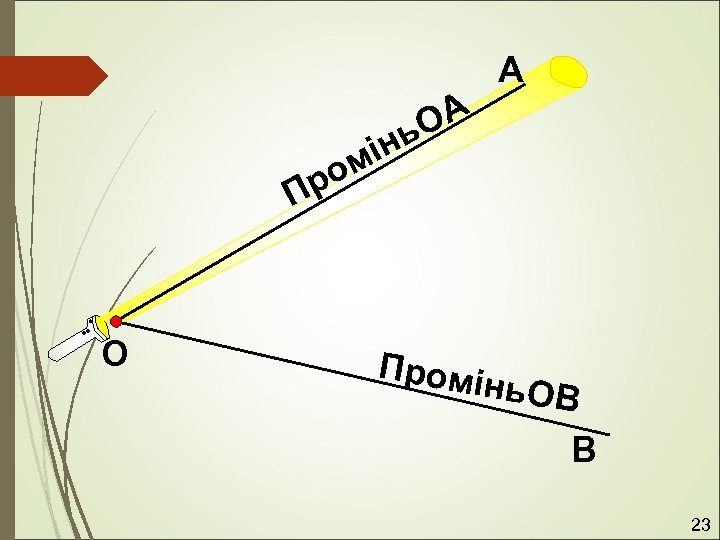
А А О нь мі ро П О Промі нь. ОВ В 23
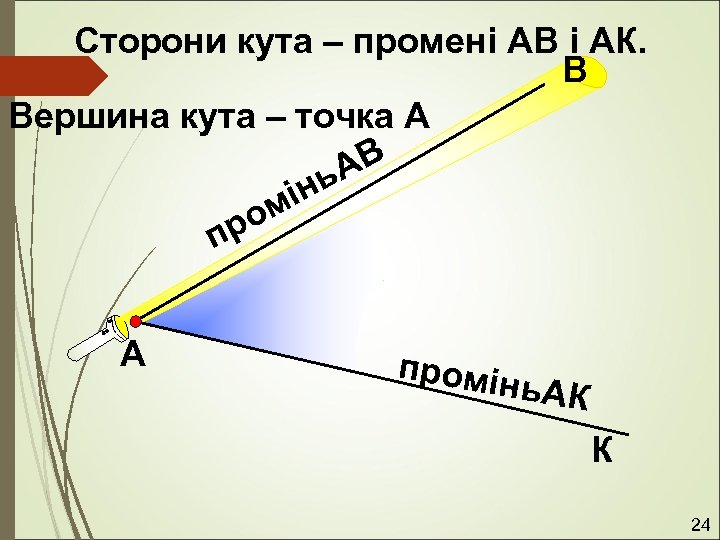
Сторони кута – промені АВ і АК. В Вершина кута – точка А АВ нь мі ро п А промін ь. АК К 24
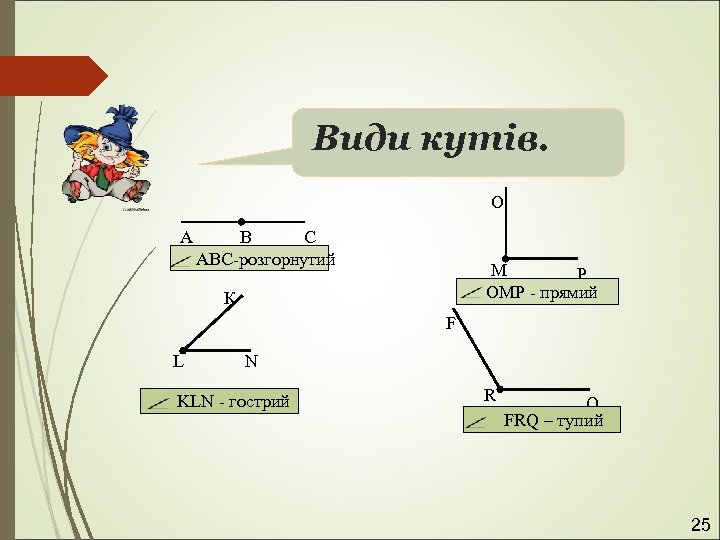
Види кутів. О А В С АВС-розгорнутий М Р ОМР - прямий К F L N KLN - гострий R Q FRQ – тупий 25
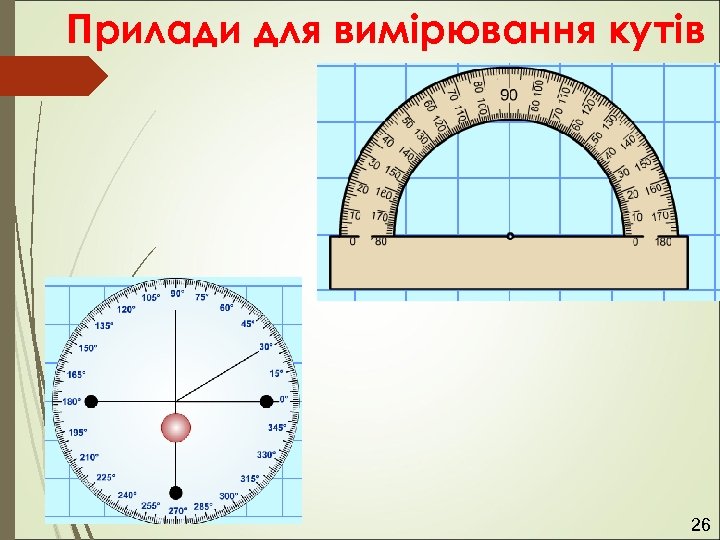
Прилади для вимірювання кутів 26

27
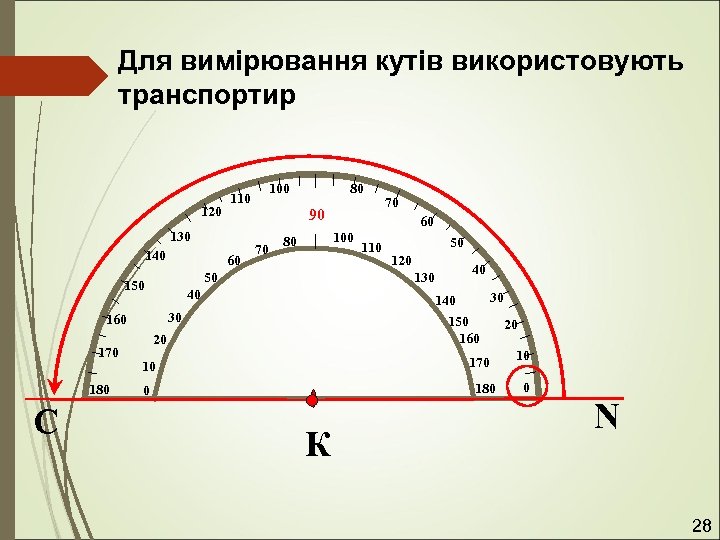
Для вимірювання кутів використовують транспортир 120 130 140 60 С 90 70 70 60 100 80 110 50 120 40 130 40 30 160 180 80 50 170 100 110 150 160 20 170 10 180 0 К 20 10 0 N 28
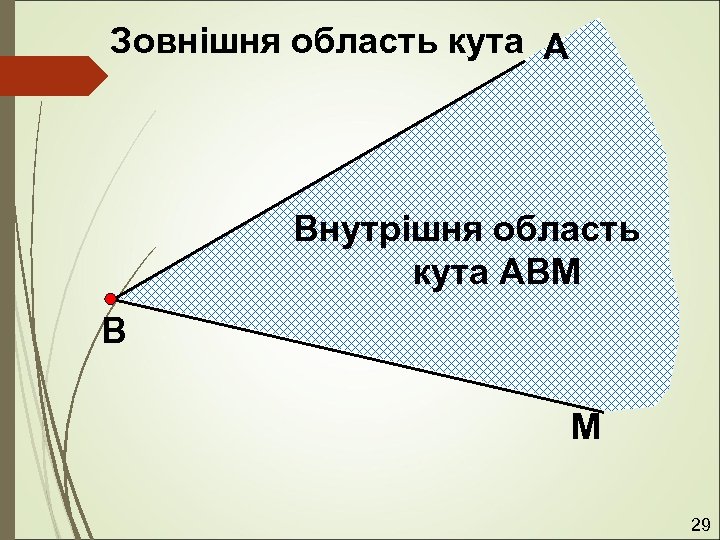
Зовнішня область кута А Внутрішня область кута АВМ В М 29
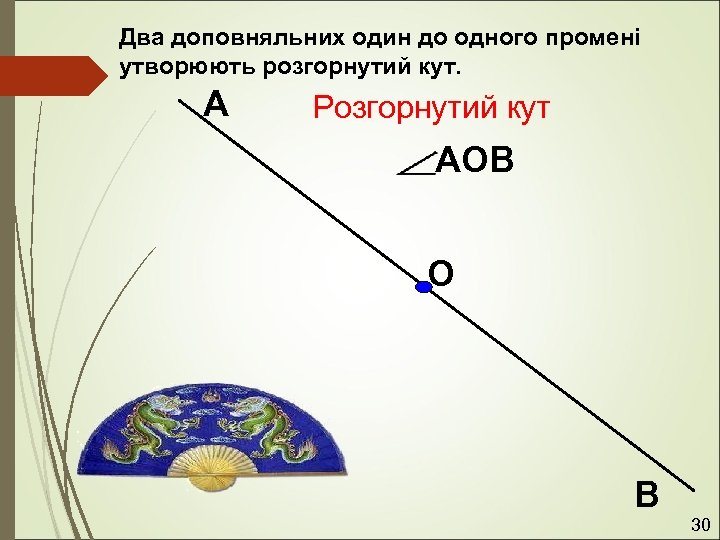
Два доповняльних один до одного промені утворюють розгорнутий кут. А Розгорнутий кут АОВ О В 30
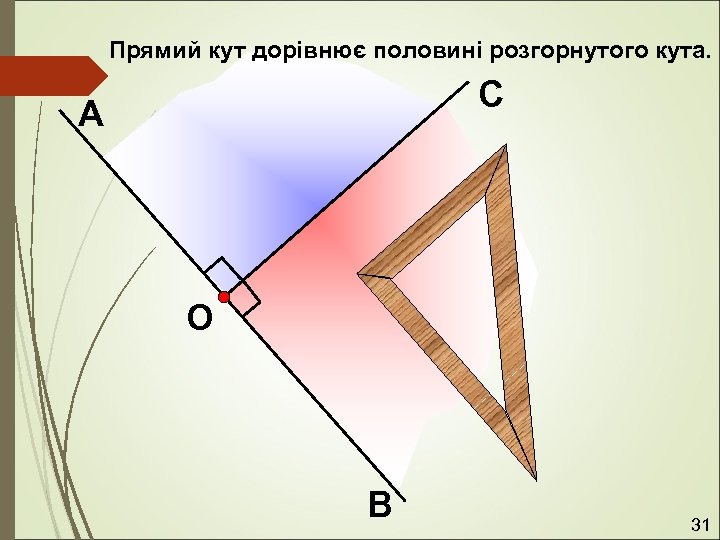
Прямий кут дорівнює половині розгорнутого кута. С А О В 31
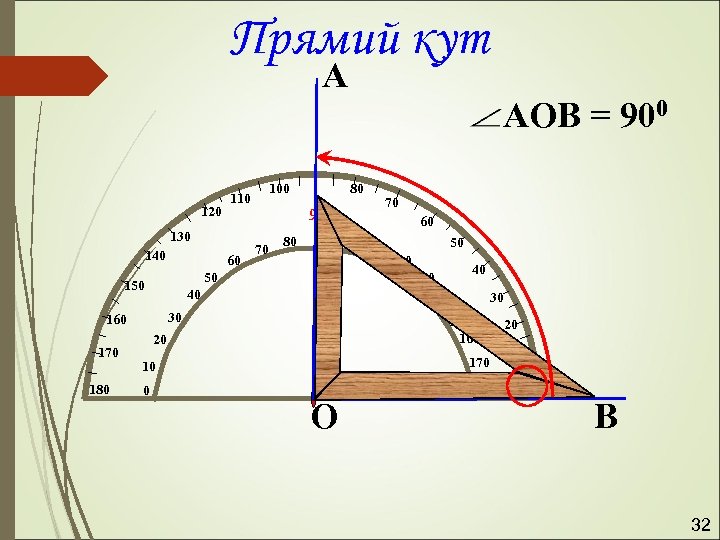
Прямий кут А 120 130 140 60 90 70 80 100 110 50 120 40 130 30 140 30 150 160 20 170 10 0 70 60 40 160 180 80 50 170 100 110 АОВ = 900 180 О 20 10 0 В 32
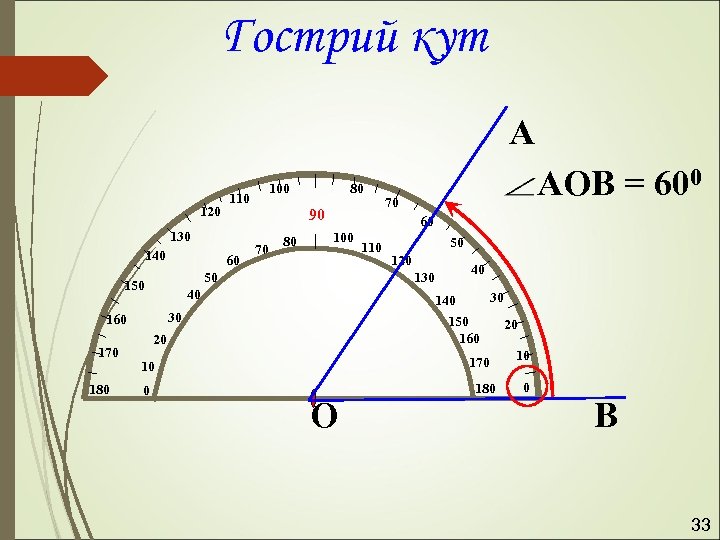
Гострий кут А 120 110 130 140 60 90 70 80 100 70 110 50 120 40 130 30 140 30 150 160 20 170 10 0 АОВ = 600 60 40 160 180 80 50 170 100 О 180 20 10 0 В 33
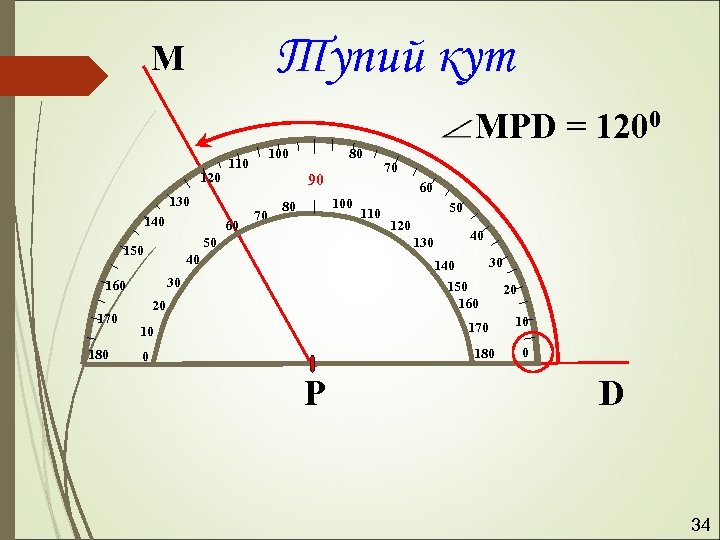
Тупий кут М MPD = 1200 120 130 140 60 90 70 70 60 100 80 110 50 120 40 130 40 30 160 180 80 50 170 100 110 150 160 20 170 10 180 0 Р 20 10 0 D 34
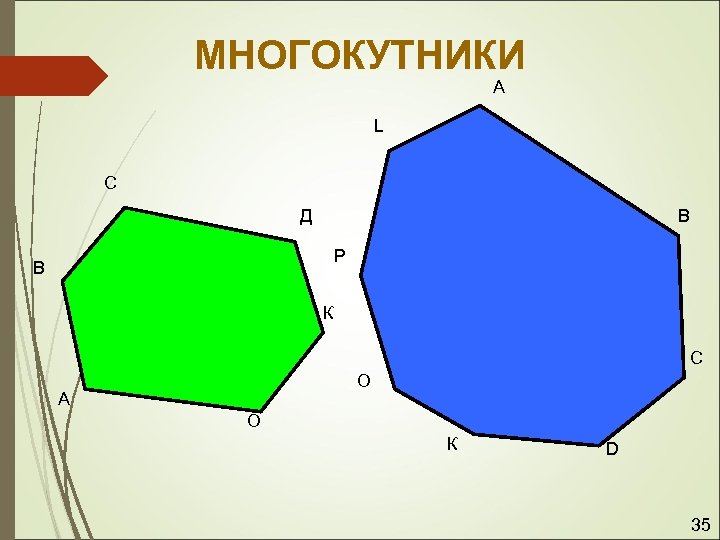
МНОГОКУТНИКИ А L С В Д P В К С О А О К D 35
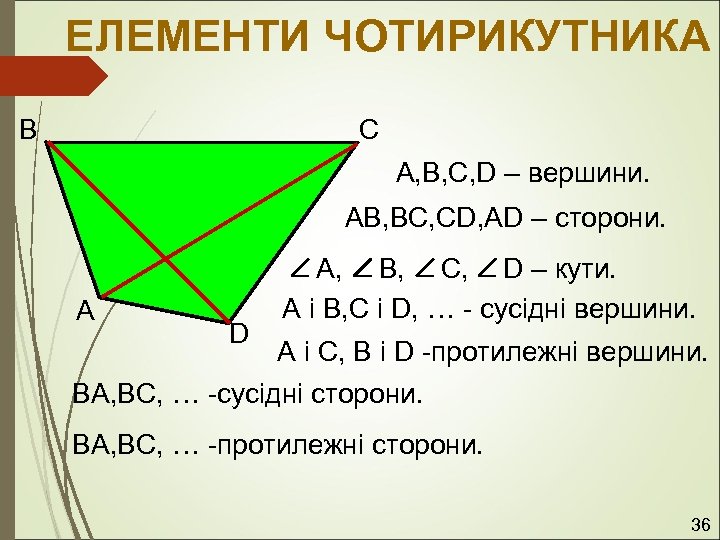
ЕЛЕМЕНТИ ЧОТИРИКУТНИКА B C A, B, C, D – вершини. AB, BC, CD, AD – сторони. A D A, B, C, D – кути. A і B, C і D, … - сусідні вершини. A і C, B і D -протилежні вершини. BA, BC, … -сусідні сторони. BA, BC, … -протилежні сторони. 36
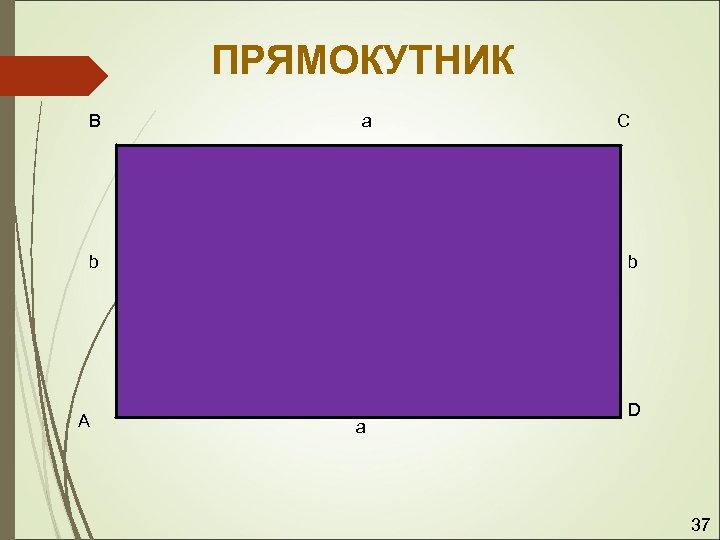
ПРЯМОКУТНИК B a b A C b a D 37

ПЕРИМЕТР ПРЯМОКУТНИКА B a C b A b a D Р=2·a+2·b P=2·(a+b) 38
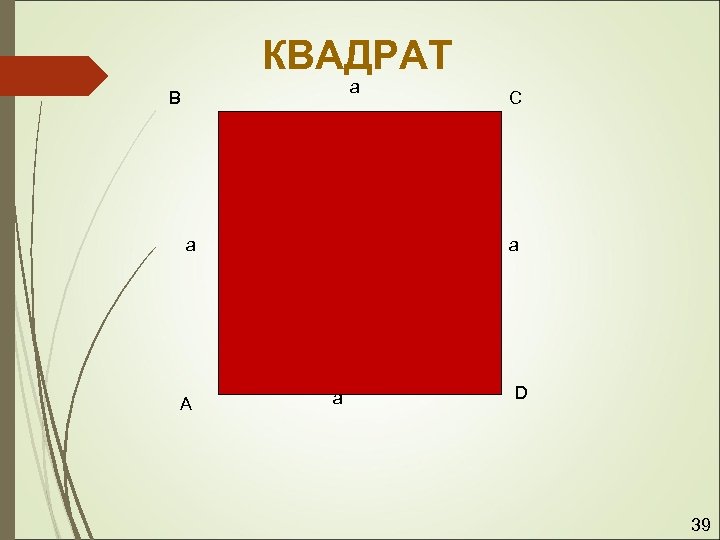
КВАДРАТ a B a A C a a D 39
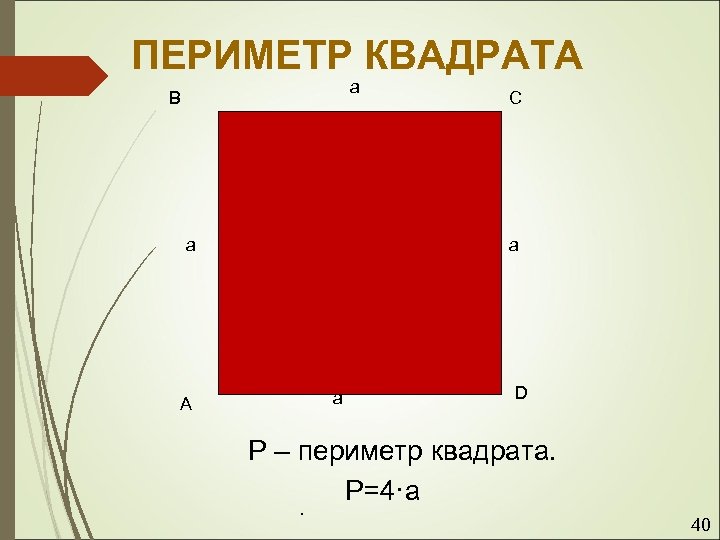
ПЕРИМЕТР КВАДРАТА a B a C a a A D Р – периметр квадрата. Р=4·а. 40
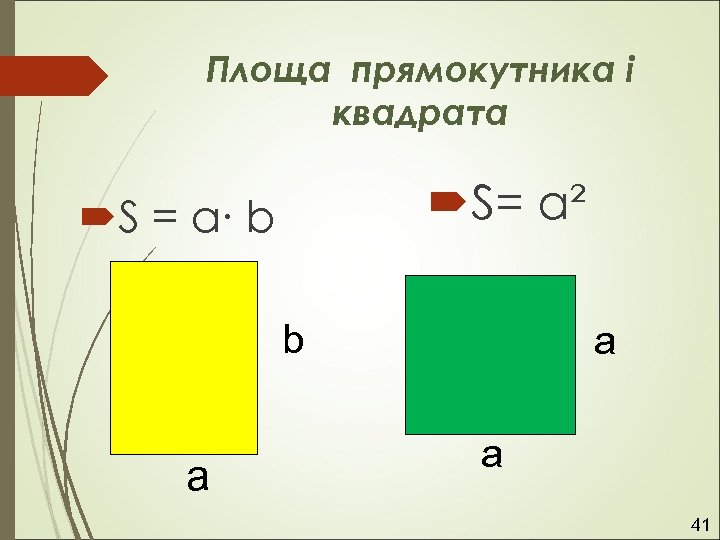
Площа прямокутника і квадрата S= a² S = a∙ b b a a a 41
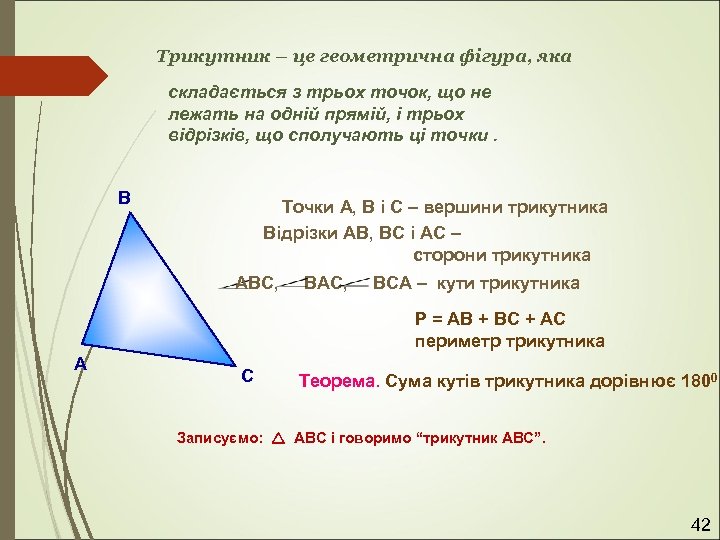
Трикутник – це геометрична фігура, яка складається з трьох точок, що не лежать на одній прямій, і трьох відрізків, що сполучають ці точки. В Точки А, В і С – вершини трикутника Відрізки АВ, ВС і АС – сторони трикутника АВС, ВАС, ВСА – кути трикутника Р = АВ + ВС + АС периметр трикутника А С Теорема. Сума кутів трикутника дорівнює 1800 Записуємо: АВС і говоримо “трикутник АВС”. 42
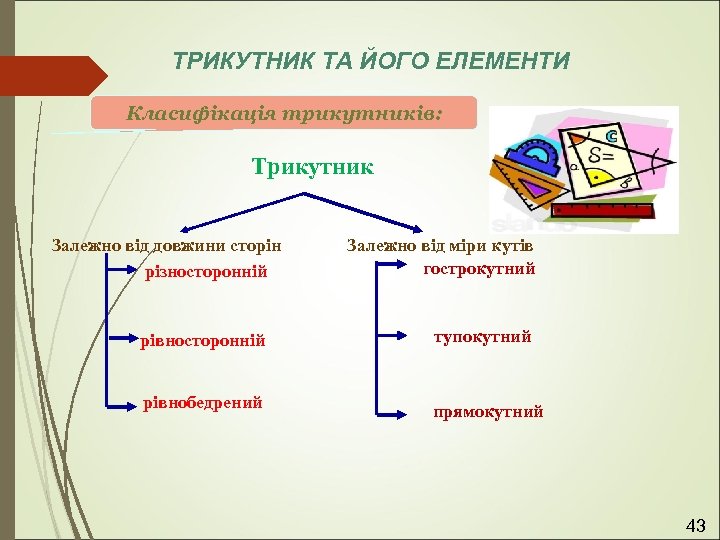
ТРИКУТНИК ТА ЙОГО ЕЛЕМЕНТИ Класифікація трикутників: Трикутник Залежно від довжини сторін різносторонній Залежно від міри кутів гострокутний рівносторонній тупокутний рівнобедрений прямокутний 43

Множення і ділення натуральних чисел. 44
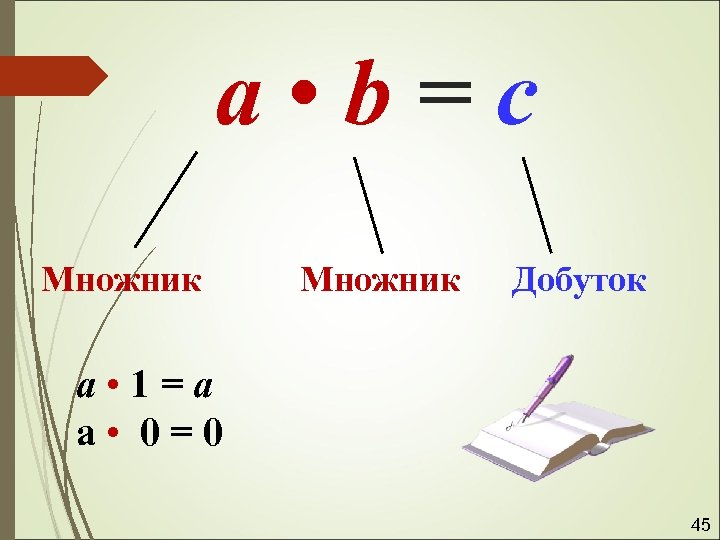
a • b=c Множник Добуток а • 1=а а • 0=0 45
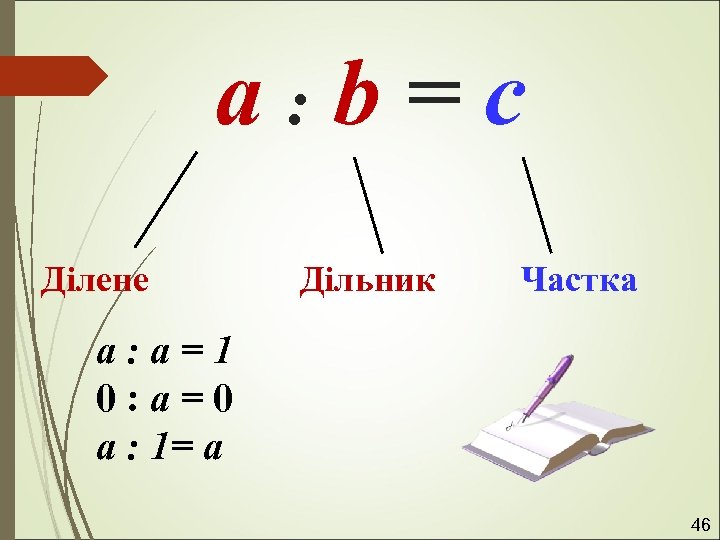
a: b=c Ділене Дільник Частка а: а=1 0: а=0 а : 1= а 46

Властивості множення: а • в = в • а (а • в) • с = а • (в • с) а(в + с) = ав + ас а(в – с) = ав - ас 47

1. Щоб знайти невідоме ділене, треба дільник помножити на частку. 2. Щоб знайти невідомий дільник, треба ділене поділити на частку. 3. Щоб знайти невідомий множник , треба добуток поділити на відомий множник. 48

Степінь числа. Вираз 9 • 9 • 9 = 95. Вираз 95 називають степенем і читають “ дев'ять у п'ятому степені ” або “дев'ять в степені п'ять ”. 95 показник степеня основа степеня Другий степінь називають квадратом, а третій – кубом числа 49

Зверни увагу! Піднесення числа до степеня – це нова, п'ята, арифметична дія. Якщо у числовий вираз входить степінь, то спочатку виконується піднесення до степеня, а потім інші дії. Наприклад, 5 • 3 2 = 5 • 9 = 45 6 + 3 2 = 6 + 9 = 15 50

Звичайні дроби 51

Звичайні дроби 52

і Чисельник Знаменник дробу показує на скільки рівних частин поділили щось ціле, а чисельник – скільки таких частин взяли. . 53
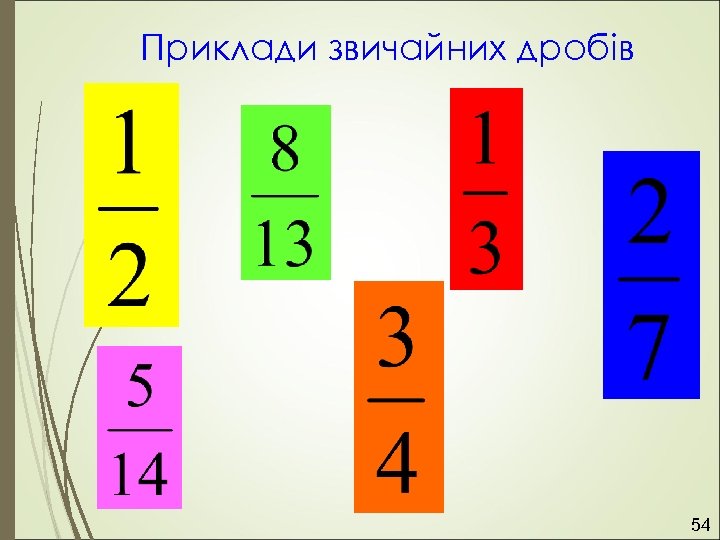
Приклади звичайних дробів 54
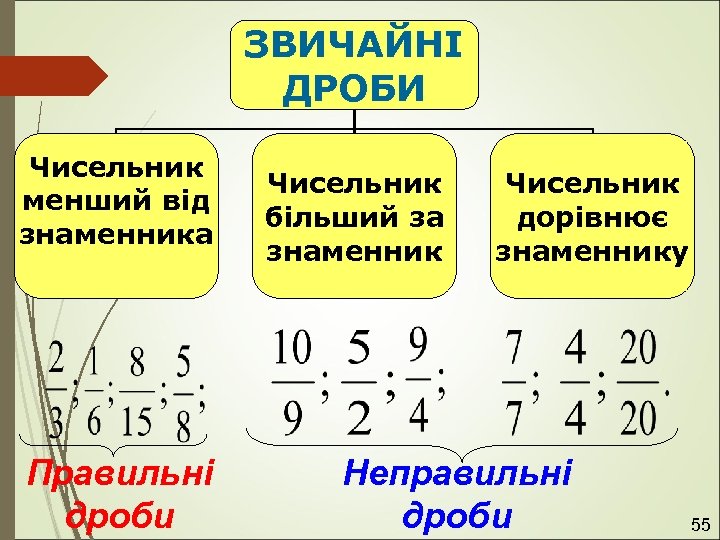
ЗВИЧАЙНІ ДРОБИ Чисельник менший від знаменника Правильні дроби Чисельник більший за знаменник Чисельник дорівнює знаменнику Неправильні дроби 55

Додавання дробів А як дроби додаємо – Всі чисельники візьмемо. Непорушна лиш “Земля”, Бо для всіх одна вона 56

Віднімання дробів Дроби віднімаємо Добре пам'ятаємо, Віднімемо чисельники, Не змінимо знаменники 57

Множення дробів Чисельник множим на чисельник А знаменник на знаменник, З результатом йдемо вкрок, Бо ми маємо добуток 58

Ділення дробів Якщо перший дріб візьмемо А другий враз перевернемо – Маємо добуток, а не казку, А спочатку була частка 59

Мішані дроби Дуже любимо ці справи, Наче іграшки, забави. Мозок свій тренуємо, Числа всі шануємо: Мішані й неправильні – Всі обчислим правильно 61

Порівняння звичайних дробів з одиницею Кожний правильний дріб менший за 1, а кожний не правильний дріб більший за будь який правильний дріб. Порівняння дробів: а>c. в<c. 61
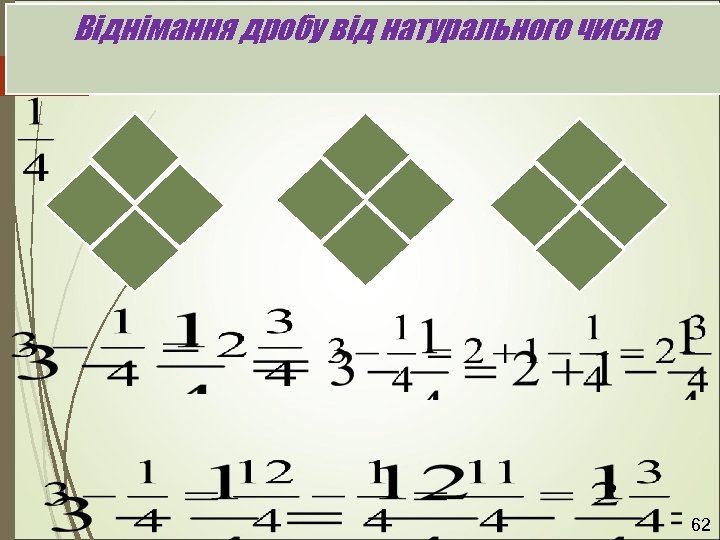
Віднімання дробу від натурального числа 62
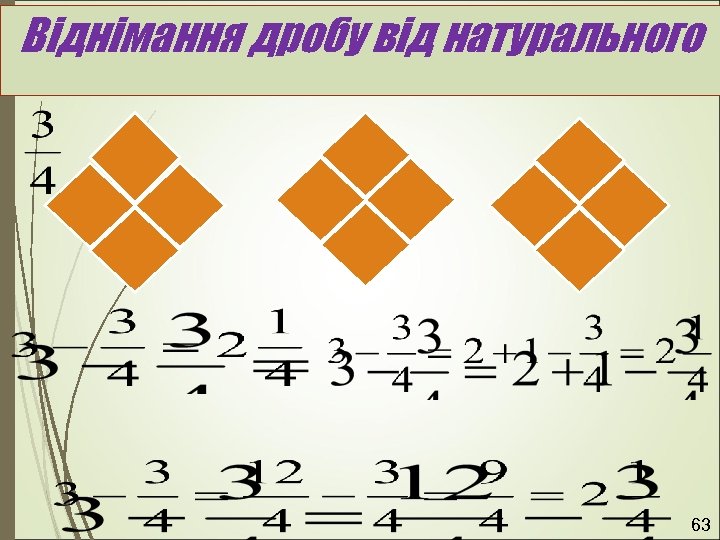
Віднімання дробу від натурального 63
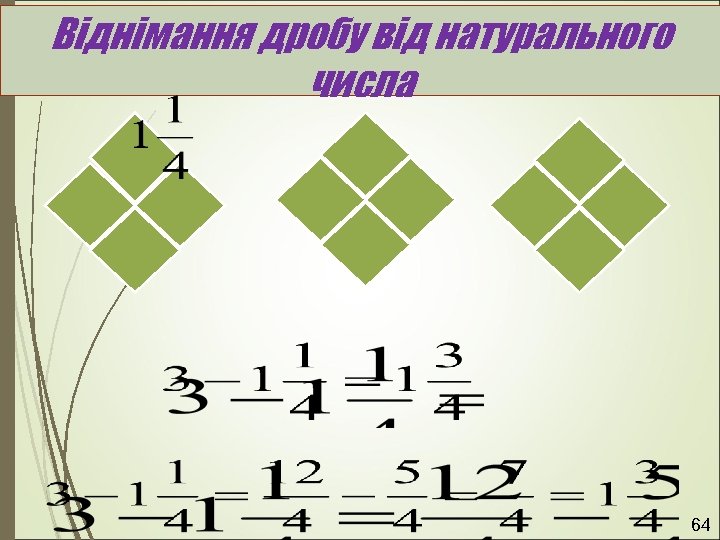
Віднімання дробу від натурального числа 64

Десяткові дроби. 65

Уявлення про десяткові дроби. 1 мм = см; 1 к. = грн. ; 1 г = кг. Для таких дробів знайшли зручну, “одноповерхову” форму запису: =0, 1 =0, 001 66

Записані в такій формі дроби, в яких знаменники є степенями десяти, тобто числами 10, 1000 і т. д. , називають десятковими дробами. = 0, 7 =0, 15 = 2, 325 67
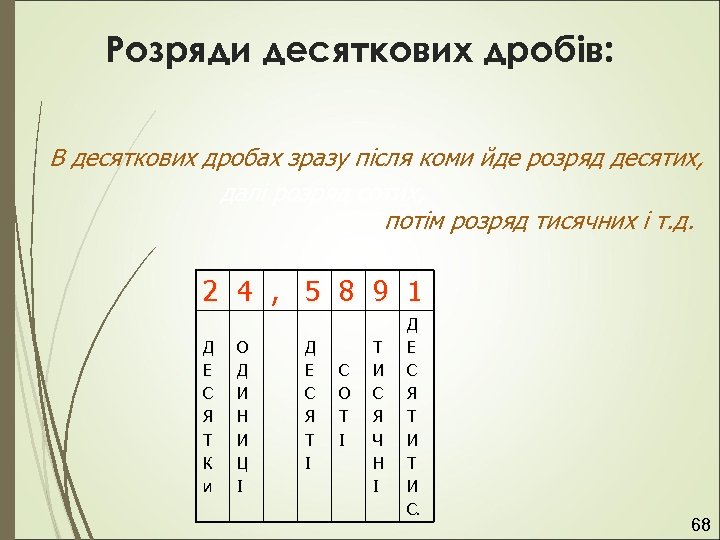
Розряди десяткових дробів: В десяткових дробах зразу після коми йде розряд десятих, далі розряд сотих, потім розряд тисячних і т. д. 2 4 , 5 8 9 1 Д Е С Я Т К и О Д И Н И Ц І Д Е С Я Т І С О Т І Т И С Я Ч Н І Д Е С Я Т И С. 68

Нуль цілих Зверніть увагу, запис дробової частини містить стільки цифр, скільки нулів у запису знаменника відповідного звичайного дробу. =0, 6 Одна цифра після коми 45 цілих Дві цифри після коми Нуль цілих Один нуль =45, 05 45 цілих Два нулі Зверніть увагу, якщо в запису чисельника не дістає цифр, то дописуємо нулі зразу після коми (зліва від числа). 69
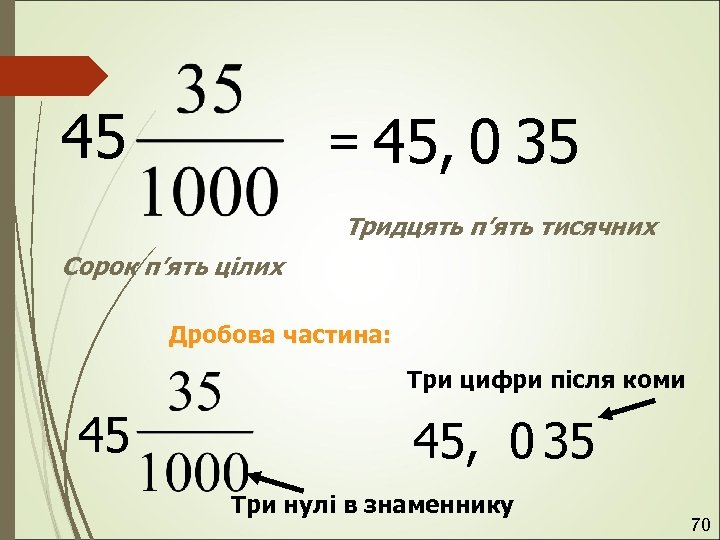
45 = 45, 0 35 Тридцять п’ять тисячних Сорок п’ять цілих Дробова частина: Три цифри після коми 45 45, 0 35 Три нулі в знаменнику 70

Порівняння десяткових дробів. 5, 258 і 4, 888 5>4 З двох десяткових дробів більший той, у якого ціла частина більша. Якщо у двох десяткових дробів ціла частина однакова, тоді порівнюємо порозрядно дробову частину. 71

Порівнюємо порозрядно (кількість цифр у дробових частинах дробу повинна бути однаковою) 1. Який з дробів більший? 4, 6 чи 4, 60 Порівняємо відрізки, довжина яких 4, 6 м і 4, 60 м: 4, 6 м= м = 4 м 6 дм = 460 см 4, 60 м= м = 4 м 60 см = 460 см 4, 6 = 4, 60 Отже, якщо до десяткового дробу справа дописати будь-яку кількість нулів, то отримаємо дріб, який дорівнює даному. 72

Щоб порівняти два десяткові дроби з рівними цілими частинами, треба за допомогою приписування нулів справа зрівняти кількість цифр у дробових частинах, після чого порівняти отримані дроби. Більше буде той дріб, дробова частина якого більша. 5, 7 > 5, 126 5, 700 5, 126 700 > 126 74

Множення десяткових дробів 75

Правило множення десяткових дробів Потрібно: 1. помножити, не звертаючи уваги на коми 2. в результаті відділити стільки знаків після коми, скільки знаків після коми в обох множниках разом 76

Окремі випадки множення Запам'ятай 77

Окремі випадки множення Запам'ятай 78

Окремі випадки множення Запам'ятай 79

Окремі випадки множення Запам'ятай 80

Ділення десяткового дробу на десятковий дріб Правило: Щоб поділити десятковий дріб на десятковий , треба : 1. Перенести в діленому і в дільнику коми вправо на стільки цифр , скільки їх міститься після коми в дільнику ; 2. Виконати ділення на натуральне число. 81

Ділення десяткового дробу на десятковий дріб Правило : Щоб поділити десятковий дріб на 0, 1 ; 0, 01 ; 0. 001 …, треба в даному дробі перенести кому праворуч на стільки цифр , скільки цифр стоїть після коми в числі , на яке ділимо. 82

ВІДСОТКИ 83

Відсотки навколо нас 84

Що ви знаєте про відсотки? Слово «процент» походить від латинських слів pro і centum, які означають «від сотні» ( звідси українською «відсоток» ) 85

Як з’явились відсотки? Знак «%» походить, як вважають, від італійського слова cento (сто), яке в процентних розрахунках часто писалося скорочено cto. Існує й інша версія виникнення цього знака: він з’явився в результаті безглуздої помилки, вчиненої видавцем. У 1685 році в Парижі була опублікована книга – “Керівництво по комерційній арифметиці”, де помилково набірник замість cto ввів %. 86

Як з’явились відсотки? Відсотки були відомі індусам у V столітті. В Європі десяткові дроби з’явились на 1000 років пізніше. Їх ввів Бельгійський вчений Сімон Стевін. Він у 1584 році вперше опублікував таблицю процентів. 87
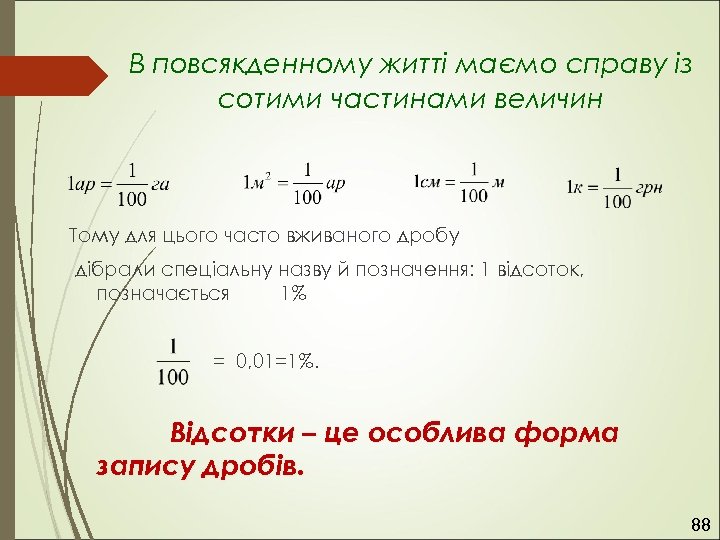
В повсякденному житті маємо справу із сотими частинами величин Тому для цього часто вживаного дробу дібрали спеціальну назву й позначення: 1 відсоток, позначається 1% = 0, 01=1%. Відсотки – це особлива форма запису дробів. 88

Що називають відсотком? 89

Перетворення відсотків у десяткові і звичайні дроби 1 % = 0, 01 = 2 % = 2· 0, 01 = 0, 02 = 15 % = 15· 0, 01 = 0, 15 = 100 % = 100· 0, 01 = 1 125 % = 125· 0, 01 = 1, 25 = 90

Перетворення десяткових дробів у відсотки 2 = 2· 100% = 200 % 1, 5 = 1, 5· 100% = 150 % 0, 3 = 0, 3· 100% = 30 % 0, 75 = 0, 75· 100% = 75 % 0, 125 = 0, 125· 100% = 12, 5 % 91

Список використаних джерел 1. Бевз Г. П. Методика викладання математики. Київ. Головне видавництво видавничого об’єднання «Вища школа» 1977 2. Мерзляк А. Г. , Полонський В. Б. . Якір М. С. Підручник для 5 класу зогальноосвітніх навчальних закладів. Харків «Гімназія» 2013. 3. Пометун О. Пироженко Л. Сучасний урок. Інтерактивні технології навчання. – Київ, 2004 4. http: //www. ime. edu-ua. net - інститут інформаційних технологій і засобів навчання Академії педагогічних наук України. 5. http: //ite. ksu. ks. ua – інформаційні технології в освіті ( фахове наукове видання). 6. http: //ua. partnersinlearningnetwork. com – освітня мережа Майкрософт « Партнерство в навчанні» . 7. http: //man. gov. ua – Мала академія наук ( сайт). 8. http: //www. iod. gov. ua – інститут обдарованої дитини АПН України. 92
21236db141afd5f16b49ab1ce807c98a.ppt