МАТЕМАТИЧНА ЛОГІКА Час – 4 год
План • Алгебра висловлювань. • Закони математичної логіки. • Розв'язування логічних задач.
В давнину різні мислителі пробували давати рецепт правильних умовиводів, які від істинних посилань призводять тільки до істинних висновків. Таких мислителів називали логіками. Наука встановила загальні методи правильних умовиводів, званих формальною логікою. Термін «логіка» походить від давньогрецького logos, що означає «слово, думка, поняття, міркування, закон» .
Поняття - це форма мислення, в якій відображені суттєві (відмінні) властивості об'єктів. Судження - це форма мислення, що відображає зв'язок понять один з одним. Умовивід - це процес отримання нового судження-висновку з одного або кількох даних суджень. Висловлювання - це будь-яке речення будьякої мови (твердження), зміст якого можна визначити як істинне або хибне. Предикат - висловлювання, що містить одне або декілька невідомих.
Будь-яке висловлювання або істинне, або хибно; бути одночасно і тим і іншим воно не може. Формулювання може будь-якої теореми є висловлюванням. Висловлювання можуть виражатися за допомогою математичних, фізичних, хімічних та інших знаків. З двох числових виразів можна скласти висловлювання, з'єднавши їх знаками рівності або нерівності.
Самі числові вирази висловлюваннями не є. Не є висловлюваннями рівняння або нерівності, що містять змінні. Наприклад, вираз X <12 стає висловлюванням при заміні змінної яким-небудь конкретним значенням. Такі речення називають висловлювальними формами.
Висловлення називається простим (елементарним), якщо ніяка його частина сама не є висловлюванням. Якщо умова не виконується, висловлювання називається складним. В алгебрі логіки, як і у звичайній алгебрі, вводиться ряд операцій.
1. Алгебра висловлювань
На сьогоднішній день в логіці існує декілька символік для позначення логічних операцій. Щоб уникнути плутанини корисно мати на увазі наступну таблицю:
Дії та перетворення, які застосовуються в звичайній алгебрі, в якій буквами позначаються числа, ґрунтуються на невеликому числі визначень і формул.
Зазначені десять формул є основними законами звичайної арифметики і алгебри. Джордж Буль, що дав у 1847 р. перше виклад алгебри логіки, зробивши припущення, що букви в записаних десяти формулах позначають не числа, а висловлювання, і показав, що можна вибрати такі визначення дій додавання і множення, при яких всі десять формул залишаються в силі.
В алгебрі логіки «сума» а + Ь називається диз'юнкцією і знак + позначається знаком V (першою літерою латинського слова «vel» - або). Сума двох висловлювань вважається хибною і рівною нулю тоді і тільки тоді, коли обидва доданки хибні, тобто 0 + 0 = 0.
В алгебрі логіки «множення» називається кон'юнкцією і позначається особливим знаком ˄. Добуток а • b двох висловлювань а і b є складним висловленням. Воно вважається істинним (рівним одиниці) тоді і тільки тоді, коли обидва співмножники істинні, і хибним (рівним нулю), якщо хоч один з співмножників хибний. Це визначення добутку відповідає звичайній арифметиці: 1 х1 = 1; 1 х0 = 0 х1 = 0; 0 х0 = 0.
Встановивши дані визначення додавання і множення, легко довести, що всі десять правил звичайної алгебри залишаються вірними і в алгебрі логіки
Доведення переставних законів
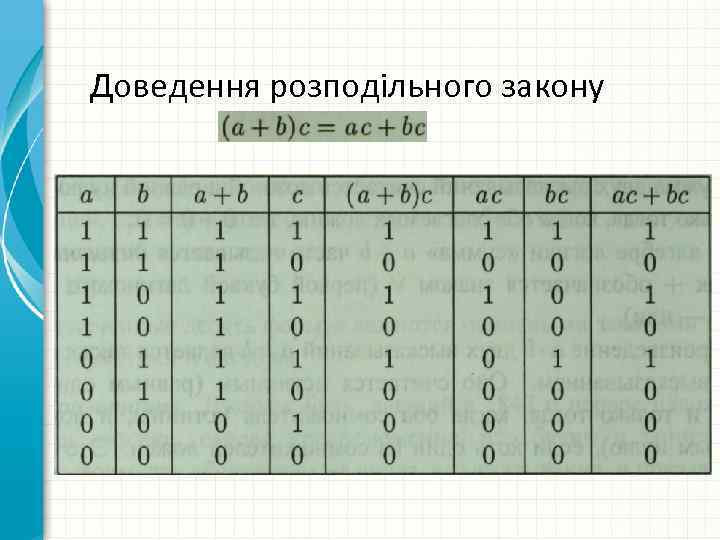Доведення розподільного закону
Деякі особливості алгебри висловлювань. В алгебрі висловлювань вводиться дію, якої немає в звичайній алгебрі - заперечення даного вислову. Для кожного висловлювання а існує його заперечення «не -а» , яке будемо позначати символом а. Якщо вислів а істинний (і), то його заперечення хибне (х); якщо а хибний, то його заперечення істинне.
Це можна виразити таблицями: З визначення смислу дії заперечення, саме з того положення, що з протилежних висловлювань завжди істинно одне і тільки одне, слідують нові формули алгебри логіки:
Можна зробити висновок: оскільки всі основні формули звичайної алгебри вірні і для алгебри висловлювань, то всі перетворення, що вживаються в звичайній алгебрі при вирішенні рівнянь, залишаються вірними і в алгебрі висловлювань.
Логічні операції. В алгебрі логіки розглядаються змінні, які можуть приймати тільки два значення 0 і 1. Змінні позначають латинськими буквами x, y, z, . . . , а також х1, x 2 … Відношення еквівалентності (рівності) задовольняє наступним властивостям: • рефлексивність: х = х; • симетричність: якщо х = у, то у = х; • транзитивність: х = у і у = z, то х = z; звідси випливає принцип: якщо х = у, то в будь-якій формулі, яка містить х, замість х можна підставити y, і в результаті буде отримана еквівалентна формула.
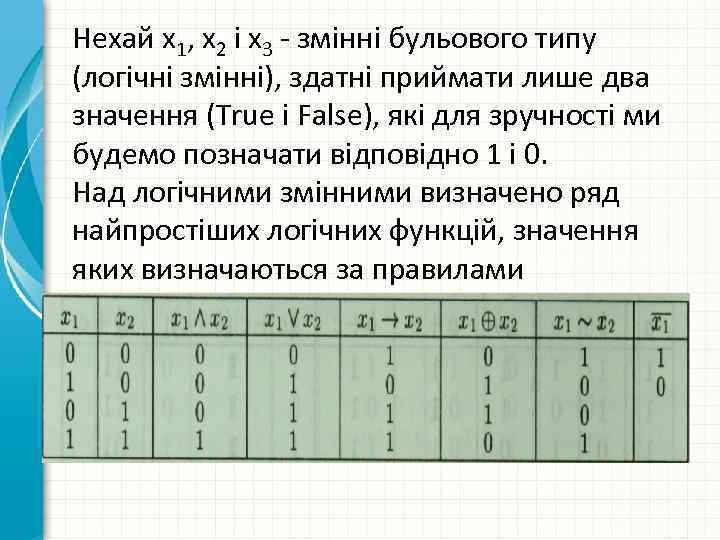Нехай х1, х2 і х3 - змінні бульового типу (логічні змінні), здатні приймати лише два значення (True і False), які для зручності ми будемо позначати відповідно 1 і 0. Над логічними змінними визначено ряд найпростіших логічних функцій, значення яких визначаються за правилами
Функції мають такі назви і позначення: • кон'юнкція (логічне множення) - ˄ (І); • диз'юнкція (логічне додавання) - V (АБО); • імплікація - →; • сума по модулю 2 - + ; • функція еквівалентності - ≡, ~, ↔ ; • заперечення (логічне заперечення) - ¬ (НЕ).
Справедливі наступні співвідношення еквівалентності між найпростішими функціями:
2. Закони математичної логіки
3. Розв'язання логічних задач
При вирішенні логічних завдань використовують прийоми: • побудова таблиці істинності; • вирішення логічних рівнянь або систем логічних рівнянь.
Для вирішення багатьох логічних задач необхідно: 1) уважно вивчити умову задачі; 2) виділити елементарні (прості) висловлювання і позначити їх літерами; 3) записати умову задачі на мові алгебри логіки, з'єднавши прості висловлювання в складні за допомогою логічних операцій; 4) скласти єдине логічне вираз для всіх вимог завдання;
5) використовуючи закони алгебри логіки, спробувати спростити отриманий вираз і обчислити всі його значення або побудувати таблицю істинності для розглянутого виразу; 6) вибрати розв'язок - набір значень простих висловлювань, при якому логічне вираз є істинним; 7) перевірити, чи задовольняє отриманий розв'язок умові задачі.
ПИТАННЯ?
ДЯКУЮ ЗА УВАГУ!!!