Математическое программирование Лекция 2 Важные частные случаи задач

Математическое программирование Лекция 2: Важные частные случаи задач линейного программирования

СОДЕРЖАНИЕ Задачи ЛП с одним ограничением. 2. Задачи ЛП на графах 3. Прямая и двойственная задачи. 4. Графическое решение задач ЛП с двумя переменными. 1.

Часть 1 Важный частный случай: задача с одним ограничением

Задача с одним видом ресурса Требуется определить вектор переменных Х, который бы максимизировал финансовые поступления на предприятие: (1) где: хi – объем выпускаемой продукции i-го вида (непрерывная неотрицательная переменная); сi – стоимость единицы выпускаемой продукции i-го вида; b – величина имеющегося ресурса (например, человекочасы); аi, – затраты единственного вида ресурса, приходящиеся на единицу i-го вида продукции.

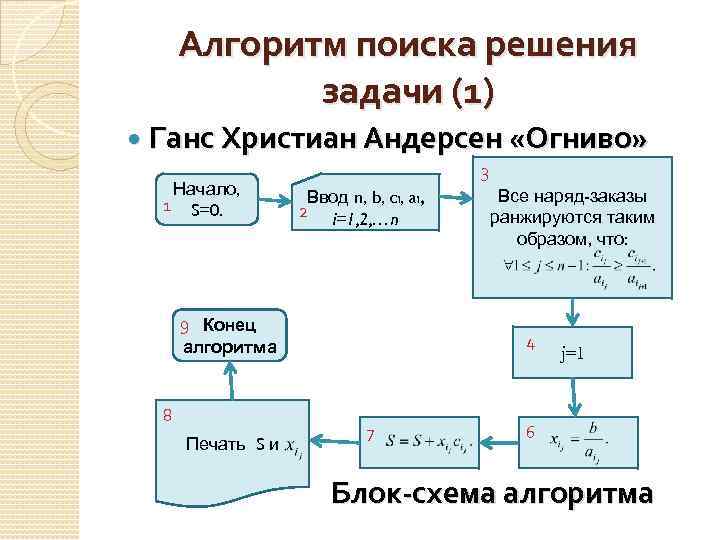Алгоритм поиска решения задачи (1) Ганс Христиан Андерсен «Огниво» Начало, 1 S=0. 3 Ввод n, b, ci, ai, 2 i=1, 2, …n 9 Конец алгоритма 8 Печать S и Все наряд-заказы ранжируются таким образом, что: 4 7 j=1 6 Блок-схема алгоритма

Достоинства и недостатки алгоритма 1. Достоинства: Гарантия глобально оптимального решения. Простота реализации. Высокое быстродействие. Низкие требования к ресурсам компьютера. 2. Недостаток: Узкий диапазон применения.

Пример 2 Решить самостоятельно, пользуясь приведенным выше алгоритмом и симплекс методом: S=5 x₁+9 x₂+3 x₃ max; 2 x₁+3 x₂+4 x₃ ≤ 12; x₁≥ 0; x₂ ≥ 0; x₃ ≥ 0. Ответ: x₁=0; x₂ =4; x₃ =0, S =36. max

Задача с одним видом ресурса и ограничениями на выпуск каждого вида продукции Требуется определить вектор переменных Х, который бы максимизировал финансовые поступления на предприятие: где: х – объем выпускаемой продукции i-го вида (непрерывная неотрицательная переменная); с – стоимость единицы выпускаемой продукции i-го вида; b – величина имеющегося ресурса (например, человекочасы); а – затраты единственного вида ресурса, приходящиеся на единицу i-го вида продукции, di - верхняя граница выпуска i-го вида продукции. i i i,

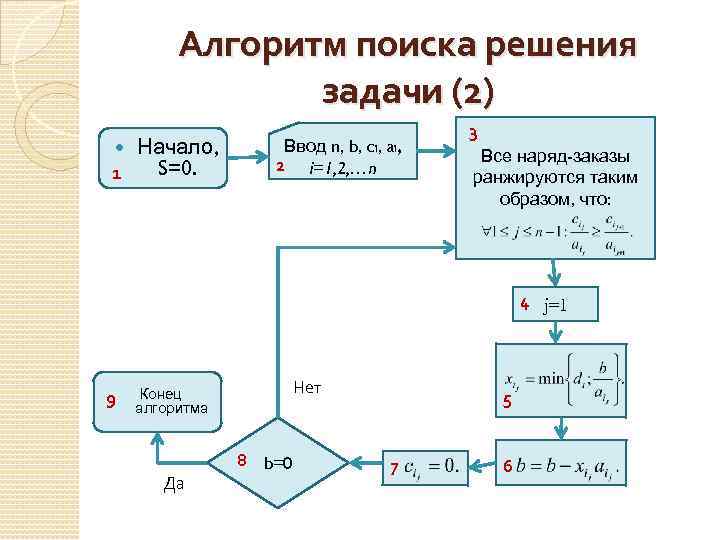Алгоритм поиска решения задачи (2) Начало, S=0. 1 Ввод n, b, ci, ai, 2 i=1, 2, …n 3 Все наряд-заказы ранжируются таким образом, что: 4 j=1 9 Нет Конец алгоритма Да 8 b=0 5 7 6

Достоинства и недостатки алгоритма 1. Достоинства: Гарантия глобально оптимального решения. Простота реализации. Высокое быстродействие. Низкие требования к ресурсам компьютера. 2. Недостаток: Узкий диапазон применения.

Пример 3 Решить самостоятельно, пользуясь приведенным выше алгоритмом и симплекс методом: S=5 x₁+9 x₂+3 x₃ max; 2 x₁+3 x₂+4 x₃ ≤ 12; 4≥x₁≥ 0; 2≥x₂ ≥ 0; 3≥x₃ ≥ 0. Ответ: x₁=3; x₂ =2; x₃=0; S=33.

Часть 2 Задачи ЛП на графах

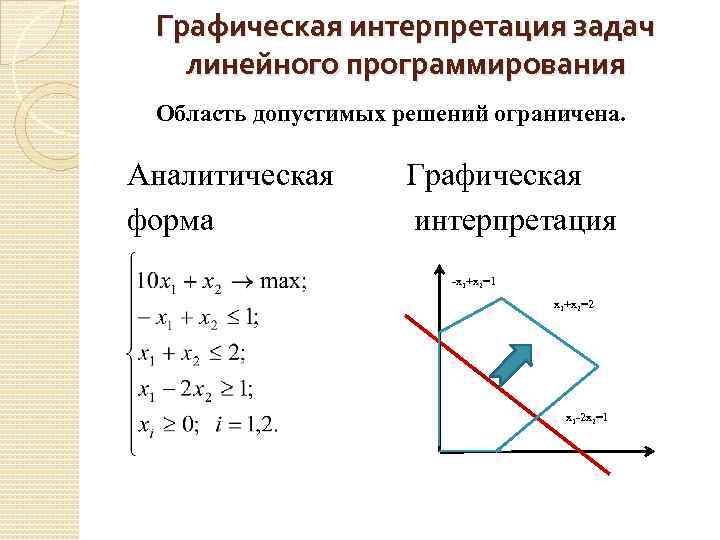Графическая интерпретация задач линейного программирования Область допустимых решений ограничена. Аналитическая форма Графическая интерпретация -x 1+x 2=1 x 1+x 2=2 x 1 -2 x 2=1

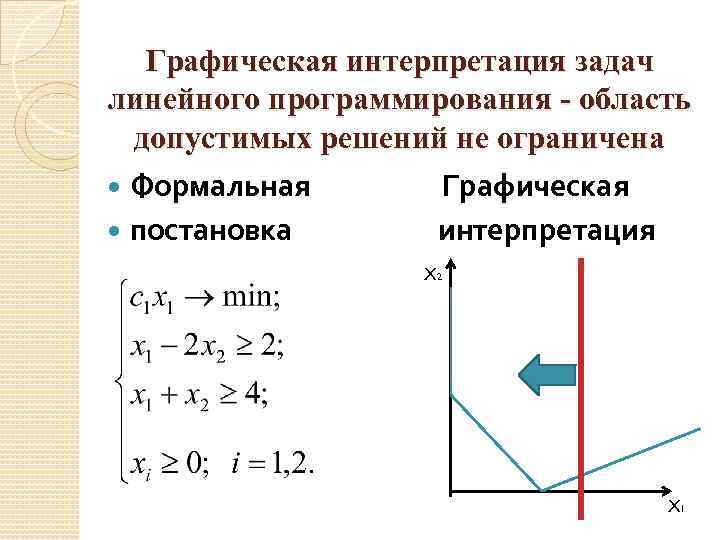Графическая интерпретация задач линейного программирования - область допустимых решений не ограничена Формальная Графическая постановка интерпретация X 2 X 1

Задачи ЛП на графах Задача о максимальном потоке: На графе G(X, U), множество вершин которого X, а множество дуг U, определить максимальный поток из вершины – источника в вершину – сток, если поток f (i, j) по дуге не может превысить пропускной способности дуги r(i, j).

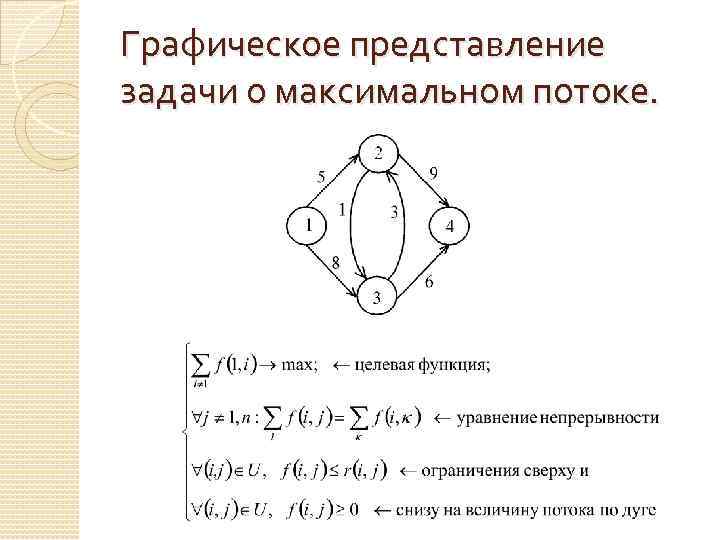Графическое представление задачи о максимальном потоке.

Задача о максимальной циркуляции на взвешенном орграфе Содержательная постановка задачи: на взвешенном орграфе с бикомпонентами требуется распределить замкнутые потоки (циркуляции) в контурах таким образом, чтобы: Их сумма в одной и той же дуге не превышала пропускной способности этой дуги. Суммарный вес всех циркуляций должен быть максимальным.

Формальная постановка задачи о максимальной циркуляции Здесь s(аi ) - циркуляция в i-о контуре; r(p, q) – пропускная способность дуги (p, q) множества U; A(p, q) – подмножество контуров, которым принадлежит дуга (p, q).

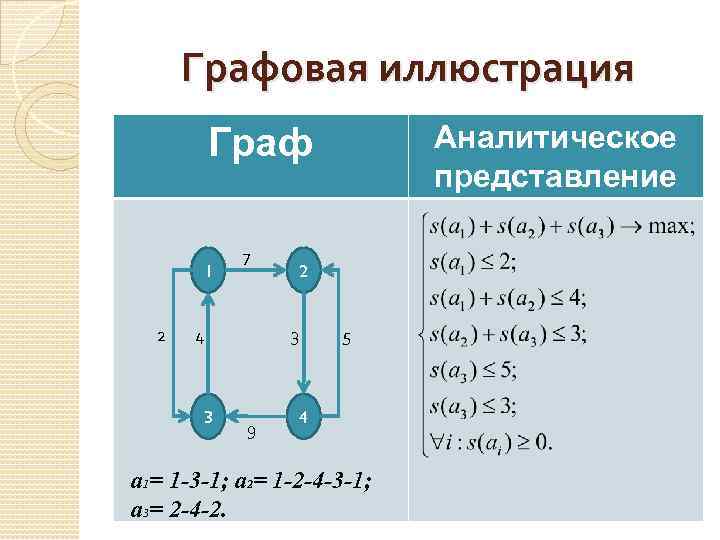Графовая иллюстрация Граф 1 7 2 2 4 3 5 3 9 4 a 1= 1 -3 -1; a 2= 1 -2 -4 -3 -1; a 3= 2 -4 -2. Аналитическое представление

Решение задачи программой поиска максимальных циркуляций на планарных графах

Часть 3. Прямые и двойственные задачи

Прямая задача

Двойственная задача Общий вид: Двойственная к задаче (1)

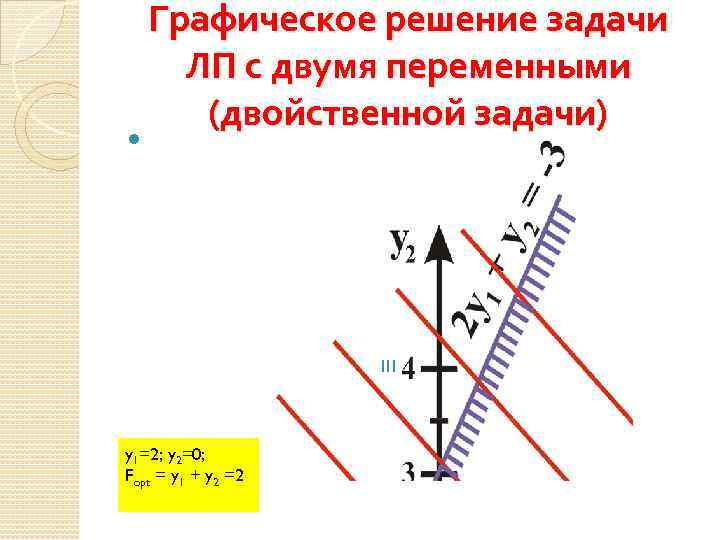Графическое решение задачи ЛП с двумя переменными (двойственной задачи) y 1=2; y 2=0; Fopt = y 1 + y 2 =2

Альтернативное описание представленных выше подходов Перейти на сайт: http: //www. matburo. ru/st_subject. php? p=mp

Часть 4 Решить задачи ЛП самостоятельно графически, используя персональные задания на следующих слайдах.

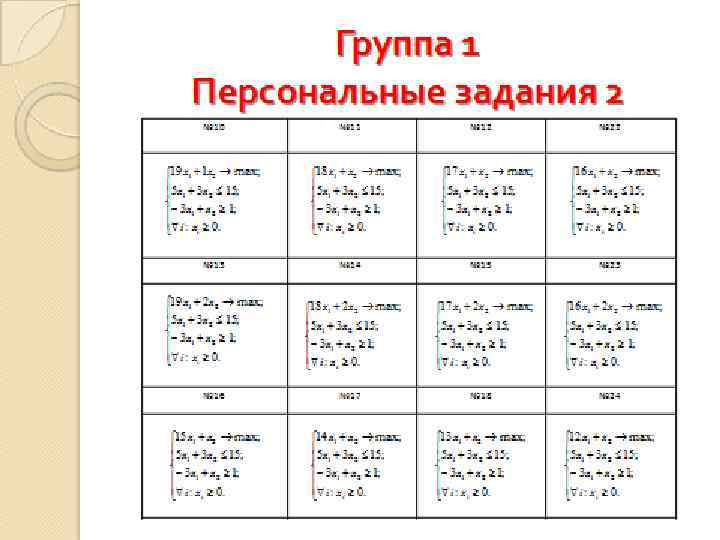
Группа 1 Персональные задания 1 № 2 № 3 № 19 № 4 № 5 № 6 № 20 № 7 № 8 № 9 № 21

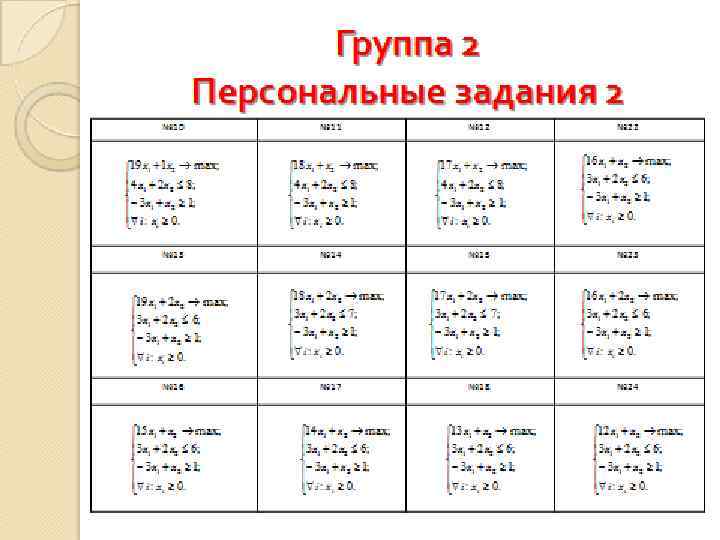
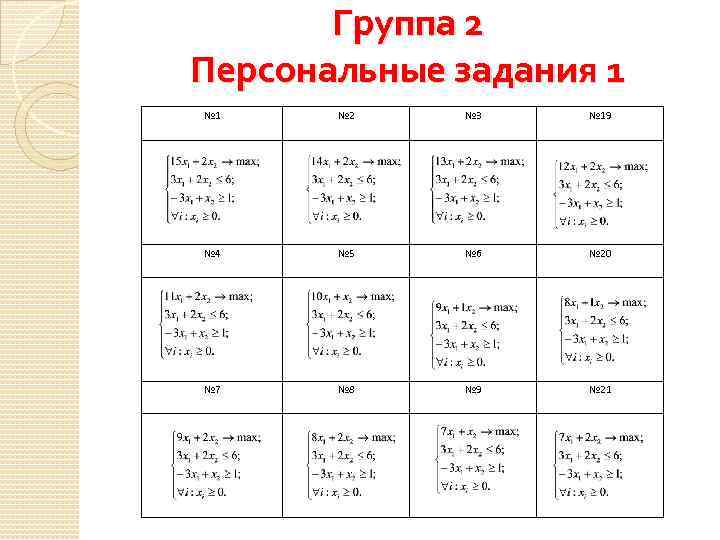Группа 2 Персональные задания 1 № 2 № 3 № 19 № 4 № 5 № 6 № 20 № 7 № 8 № 9 № 21