Введение.pptx
- Количество слайдов: 17
 МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ГИДРОДИНАМИЧЕСКИХ ПРОЦЕССОВ Преподаватель: Шарай Елена Юрьевна
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ГИДРОДИНАМИЧЕСКИХ ПРОЦЕССОВ Преподаватель: Шарай Елена Юрьевна
 Введение В гидромеханике принято объединять жидкости, газы и пар под одним названием – жидкости. Это связано с тем, что законы жидкости движения жидкостей и газов (паров) одинаковы, если их скорости значительно ниже скорости звука. Fluid (жидкость, газ) Могут иметь объём, равный объёму сосуда. Liquid (жидкость) Всегда сохраняют свой объём и принимают форму сосуда. Жидкостями называются все вещества, обладающие текучестью приложении к ним самых незначительных сил сдвига. 2
Введение В гидромеханике принято объединять жидкости, газы и пар под одним названием – жидкости. Это связано с тем, что законы жидкости движения жидкостей и газов (паров) одинаковы, если их скорости значительно ниже скорости звука. Fluid (жидкость, газ) Могут иметь объём, равный объёму сосуда. Liquid (жидкость) Всегда сохраняют свой объём и принимают форму сосуда. Жидкостями называются все вещества, обладающие текучестью приложении к ним самых незначительных сил сдвига. 2
 Гидродинамические процессы – это сложные физические процессы, включающие перемещение жидкостей, разделение суспензий, перемешивание. Участвующие в них потоки вещества, как правило, многофазные и многокомпонентные. Примеры: Для перемещения жидкостей используют различные насосы: поршневые, центробежные, струйные и др. Суспензии разделяют отстаиванием, фильтрованием, гидроциклонированием. Аэрозоли (дисперсная система, состоящая из взвешенных в газовой среде (дисперсионной среде) мелких частиц (дисперсной фазы)) разделяют фильтрованием, циклонированием, инерционным осаждением. Фильтрование – гидродинамический процесс, скорость которого прямо пропорциональна разности давлений, создаваемой по обеим сторонам фильтровальной перегородки (движущая сила процесса), и обратно пропорциональна сопротивлению, испытываемому жидкостью при ее движении через поры перегородки и слой образовавшегося осадка. 3
Гидродинамические процессы – это сложные физические процессы, включающие перемещение жидкостей, разделение суспензий, перемешивание. Участвующие в них потоки вещества, как правило, многофазные и многокомпонентные. Примеры: Для перемещения жидкостей используют различные насосы: поршневые, центробежные, струйные и др. Суспензии разделяют отстаиванием, фильтрованием, гидроциклонированием. Аэрозоли (дисперсная система, состоящая из взвешенных в газовой среде (дисперсионной среде) мелких частиц (дисперсной фазы)) разделяют фильтрованием, циклонированием, инерционным осаждением. Фильтрование – гидродинамический процесс, скорость которого прямо пропорциональна разности давлений, создаваемой по обеим сторонам фильтровальной перегородки (движущая сила процесса), и обратно пропорциональна сопротивлению, испытываемому жидкостью при ее движении через поры перегородки и слой образовавшегося осадка. 3
 Многофакторность гидродинамических процессов В ходе протекания гидродинамических процессов в каждой точке фазы и на границах раздела происходит перенос импульса, энергии, массы. Весь процесс в целом протекает в аппарате с конкретными геометрическими характеристиками, оказывающими, в свою очередь, влияние на характер этого процесса. Как же изучать гидродинамические процессы? Один из вариантов решения этой проблемы дает метод математического моделирования, базирующийся на стратегии моделирования системного анализа, сущность которой заключается в представлении процесса как сложной взаимодействующей иерархической системы с последующим качественным анализом ее структуры, разработкой математического описания, метода решения и оценкой неизвестных параметров. Такой подход позволяет наиболее полно установить совокупность явлений всего процесса и связей между ними. 4
Многофакторность гидродинамических процессов В ходе протекания гидродинамических процессов в каждой точке фазы и на границах раздела происходит перенос импульса, энергии, массы. Весь процесс в целом протекает в аппарате с конкретными геометрическими характеристиками, оказывающими, в свою очередь, влияние на характер этого процесса. Как же изучать гидродинамические процессы? Один из вариантов решения этой проблемы дает метод математического моделирования, базирующийся на стратегии моделирования системного анализа, сущность которой заключается в представлении процесса как сложной взаимодействующей иерархической системы с последующим качественным анализом ее структуры, разработкой математического описания, метода решения и оценкой неизвестных параметров. Такой подход позволяет наиболее полно установить совокупность явлений всего процесса и связей между ними. 4
 Математическое моделирование – объекта на математической модели. изучение свойств Цель математического моделирования – определение оптимальных условий протекания процесса, управление им на основе математической модели и перенос результатов на объект. Основным понятием метода математического моделирования является понятие математической модели. Математическая модель – приближенное описание какоголибо явления или процесса внешнего мира, выраженное с помощью математической символики. 5
Математическое моделирование – объекта на математической модели. изучение свойств Цель математического моделирования – определение оптимальных условий протекания процесса, управление им на основе математической модели и перенос результатов на объект. Основным понятием метода математического моделирования является понятие математической модели. Математическая модель – приближенное описание какоголибо явления или процесса внешнего мира, выраженное с помощью математической символики. 5
 Математическое моделирование включает три взаимосвязанных этапа: 1) составление математического описания изучаемого объекта. Данная задача состоит: а) в установлении связей между параметрами процесса, а также дополнительных условий, которые обычно называются граничными и начальными условиями; б) в формализации процесса в виде системы математических соотношений, характеризующих изучаемый объект. Математическое описание составляется на основе материальных и энергетических балансов, а также физических законов, определяющих переходные процессы в объектах либо характеризующих специфические особенности процесса. В систему математического описания в общем случае могут входить алгебраические уравнения, обыкновенные дифференциальные уравнения и в частных производных, эмпирические формулы, логические условия и др. 6
Математическое моделирование включает три взаимосвязанных этапа: 1) составление математического описания изучаемого объекта. Данная задача состоит: а) в установлении связей между параметрами процесса, а также дополнительных условий, которые обычно называются граничными и начальными условиями; б) в формализации процесса в виде системы математических соотношений, характеризующих изучаемый объект. Математическое описание составляется на основе материальных и энергетических балансов, а также физических законов, определяющих переходные процессы в объектах либо характеризующих специфические особенности процесса. В систему математического описания в общем случае могут входить алгебраические уравнения, обыкновенные дифференциальные уравнения и в частных производных, эмпирические формулы, логические условия и др. 6
 2) выбор метода решения системы математического описания и реализация его моделирующей программы. уравнений в форме Параметры (коэффициенты) составленных уравнений функционально зависят от определяющих размеров технологического аппарата (диаметров, длин), свойств обрабатываемых веществ (плотностей, вязкостей) и величин, характеризующих протекание физических процессов (коэффициентов диффузии, пористость материалов). Эти параметры либо задают предварительно, либо рассчитывают, или находят по формулам, вытекающим из известных критериальных зависимостей. Нередко для получения численных значений коэффициентов требуется постановка специальных лабораторных опытов по изучению каждого из происходящих в объекте процессов (пример, проницаемость). В отдельных наиболее простых случаях возможны точные аналитические решения уравнений модели. Но, как правило, объекты отличаются сложностью и для реализации их математических моделей применяется вычислительная техника. 7
2) выбор метода решения системы математического описания и реализация его моделирующей программы. уравнений в форме Параметры (коэффициенты) составленных уравнений функционально зависят от определяющих размеров технологического аппарата (диаметров, длин), свойств обрабатываемых веществ (плотностей, вязкостей) и величин, характеризующих протекание физических процессов (коэффициентов диффузии, пористость материалов). Эти параметры либо задают предварительно, либо рассчитывают, или находят по формулам, вытекающим из известных критериальных зависимостей. Нередко для получения численных значений коэффициентов требуется постановка специальных лабораторных опытов по изучению каждого из происходящих в объекте процессов (пример, проницаемость). В отдельных наиболее простых случаях возможны точные аналитические решения уравнений модели. Но, как правило, объекты отличаются сложностью и для реализации их математических моделей применяется вычислительная техника. 7
 3) установление соответствия (адекватности) модели объекту. Данный этап необходимо проводить по той причине, что любая модель является лишь приближенным отражением реального процесса вследствие допущений, всегда принимаемых при составлении математической модели. Решением этой задачи устанавливается, насколько принятые допущения правомерны, и тем самым определяется, применима ли полученная модель для исследуемого процесса. При необходимости проводится коррекция математической модели. С этой целью используются результаты измерений на самом объекте или на его физической модели, воспроизводящей в сравнительно небольших масштабах основные физические закономерности объекта моделирования. 8
3) установление соответствия (адекватности) модели объекту. Данный этап необходимо проводить по той причине, что любая модель является лишь приближенным отражением реального процесса вследствие допущений, всегда принимаемых при составлении математической модели. Решением этой задачи устанавливается, насколько принятые допущения правомерны, и тем самым определяется, применима ли полученная модель для исследуемого процесса. При необходимости проводится коррекция математической модели. С этой целью используются результаты измерений на самом объекте или на его физической модели, воспроизводящей в сравнительно небольших масштабах основные физические закономерности объекта моделирования. 8
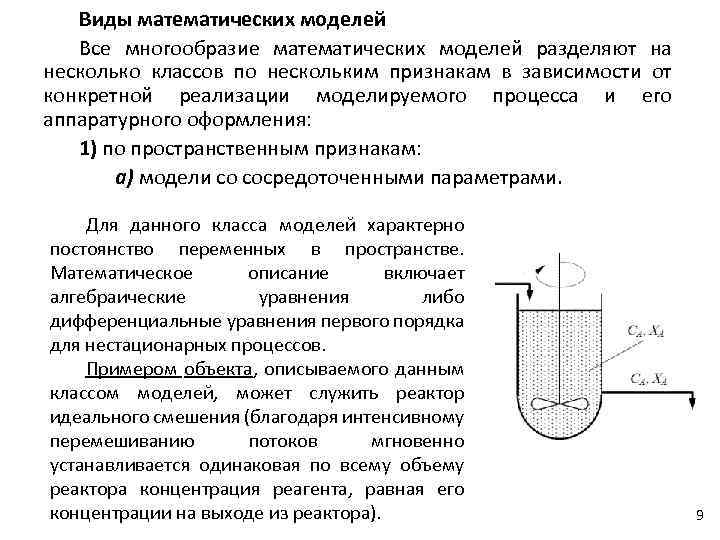 Виды математических моделей Все многообразие математических моделей разделяют на несколько классов по нескольким признакам в зависимости от конкретной реализации моделируемого процесса и его аппаратурного оформления: 1) по пространственным признакам: а) модели со сосредоточенными параметрами. Для данного класса моделей характерно постоянство переменных в пространстве. Математическое описание включает алгебраические уравнения либо дифференциальные уравнения первого порядка для нестационарных процессов. Примером объекта, описываемого данным классом моделей, может служить реактор идеального смешения (благодаря интенсивному перемешиванию потоков мгновенно устанавливается одинаковая по всему объему реактора концентрация реагента, равная его концентрации на выходе из реактора). 9
Виды математических моделей Все многообразие математических моделей разделяют на несколько классов по нескольким признакам в зависимости от конкретной реализации моделируемого процесса и его аппаратурного оформления: 1) по пространственным признакам: а) модели со сосредоточенными параметрами. Для данного класса моделей характерно постоянство переменных в пространстве. Математическое описание включает алгебраические уравнения либо дифференциальные уравнения первого порядка для нестационарных процессов. Примером объекта, описываемого данным классом моделей, может служить реактор идеального смешения (благодаря интенсивному перемешиванию потоков мгновенно устанавливается одинаковая по всему объему реактора концентрация реагента, равная его концентрации на выходе из реактора). 9
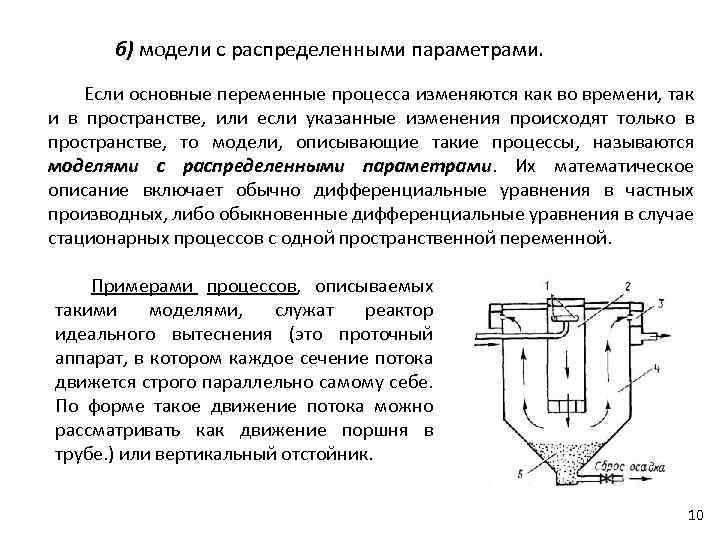 б) модели с распределенными параметрами. Если основные переменные процесса изменяются как во времени, так и в пространстве, или если указанные изменения происходят только в пространстве, то модели, описывающие такие процессы, называются моделями с распределенными параметрами. Их математическое параметрами описание включает обычно дифференциальные уравнения в частных производных, либо обыкновенные дифференциальные уравнения в случае стационарных процессов с одной пространственной переменной. Примерами процессов, описываемых такими моделями, служат реактор идеального вытеснения (это проточный аппарат, в котором каждое сечение потока движется строго параллельно самому себе. По форме такое движение потока можно рассматривать как движение поршня в трубе. ) или вертикальный отстойник. 10
б) модели с распределенными параметрами. Если основные переменные процесса изменяются как во времени, так и в пространстве, или если указанные изменения происходят только в пространстве, то модели, описывающие такие процессы, называются моделями с распределенными параметрами. Их математическое параметрами описание включает обычно дифференциальные уравнения в частных производных, либо обыкновенные дифференциальные уравнения в случае стационарных процессов с одной пространственной переменной. Примерами процессов, описываемых такими моделями, служат реактор идеального вытеснения (это проточный аппарат, в котором каждое сечение потока движется строго параллельно самому себе. По форме такое движение потока можно рассматривать как движение поршня в трубе. ) или вертикальный отстойник. 10
 2) по характеру режимов: а) статические модели Статические модели отражают работу объекта в стационарных условиях, т. е. когда параметры процесса не меняются во времени. Соответственно математическое описание в статических моделях не включает время как переменную и состоит из алгебраических уравнений либо дифференциальных уравнений в случае объектов с распределенными параметрами. б) динамические модели Динамическая модель отражает изменение объекта во времени. Математическое описание таких моделей обязательно включает производную по времени. Q = Constant Q ≠ Constant 11
2) по характеру режимов: а) статические модели Статические модели отражают работу объекта в стационарных условиях, т. е. когда параметры процесса не меняются во времени. Соответственно математическое описание в статических моделях не включает время как переменную и состоит из алгебраических уравнений либо дифференциальных уравнений в случае объектов с распределенными параметрами. б) динамические модели Динамическая модель отражает изменение объекта во времени. Математическое описание таких моделей обязательно включает производную по времени. Q = Constant Q ≠ Constant 11
 3) по природе процессов, протекающих в моделируемых объектах: а) детерминированные модели – модели, в которых значение выходной характеризующей величины однозначно определяется значением входной величины. При составлении таких моделей используют фундаментальные законы физики (перенос вещества, энергии, импульса). б) вероятностные модели – модели описывающие стохастический (случайный) процесс, в котором изменение определяющих величин происходит беспорядочно и часто дискретно. При этом значение входной величины не находится в однозначном соответствии с входной. При составлении этих моделей используют аппарат теории вероятностей, при помощи которого параметры состояния оцениваются в терминах мат. ожидания, а возмущающие параметры характеризуются вероятностными законами распределения (например, при моделировании соударения частиц друг с другом). 12
3) по природе процессов, протекающих в моделируемых объектах: а) детерминированные модели – модели, в которых значение выходной характеризующей величины однозначно определяется значением входной величины. При составлении таких моделей используют фундаментальные законы физики (перенос вещества, энергии, импульса). б) вероятностные модели – модели описывающие стохастический (случайный) процесс, в котором изменение определяющих величин происходит беспорядочно и часто дискретно. При этом значение входной величины не находится в однозначном соответствии с входной. При составлении этих моделей используют аппарат теории вероятностей, при помощи которого параметры состояния оцениваются в терминах мат. ожидания, а возмущающие параметры характеризуются вероятностными законами распределения (например, при моделировании соударения частиц друг с другом). 12
 Математическое описание процессов перемещения фаз Поведение потоков в реальных аппаратах настолько сложно, что в настоящее время дать строгое математическое описание их в большинстве случаев не представляется возможным. В то же время известно, что структура потоков оказывает существенное влияние на эффективность технологических процессов (процессы разделения), поэтому ее необходимо учитывать при моделировании. Точное описание реальных потоков приводит к чрезвычайно трудным для решения задачам. Поэтому разработанные к настоящему времени модели носят полуэмпирический характер (при учете турбулентности, соударения со стенками, взаимодействии фаз между собой). Тем не менее, они позволяют получать модели, достаточно отражающие реальный физический процесс (модели, адекватные объекту). 13
Математическое описание процессов перемещения фаз Поведение потоков в реальных аппаратах настолько сложно, что в настоящее время дать строгое математическое описание их в большинстве случаев не представляется возможным. В то же время известно, что структура потоков оказывает существенное влияние на эффективность технологических процессов (процессы разделения), поэтому ее необходимо учитывать при моделировании. Точное описание реальных потоков приводит к чрезвычайно трудным для решения задачам. Поэтому разработанные к настоящему времени модели носят полуэмпирический характер (при учете турбулентности, соударения со стенками, взаимодействии фаз между собой). Тем не менее, они позволяют получать модели, достаточно отражающие реальный физический процесс (модели, адекватные объекту). 13
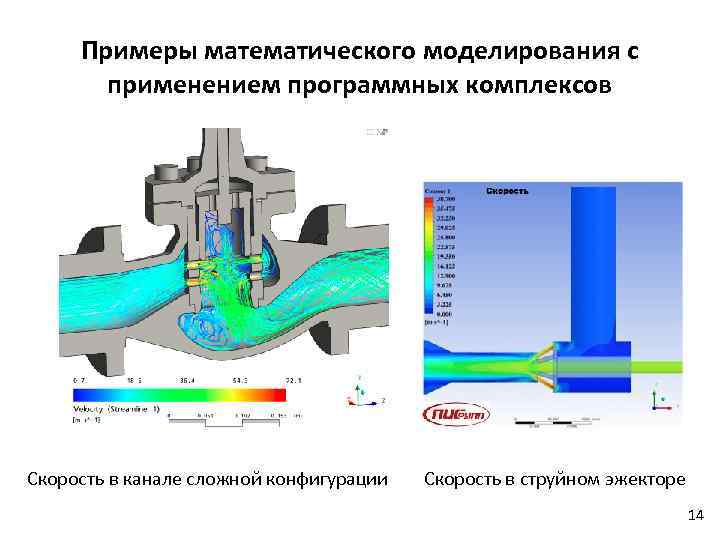 Примеры математического моделирования с применением программных комплексов Скорость в канале сложной конфигурации Скорость в струйном эжекторе 14
Примеры математического моделирования с применением программных комплексов Скорость в канале сложной конфигурации Скорость в струйном эжекторе 14
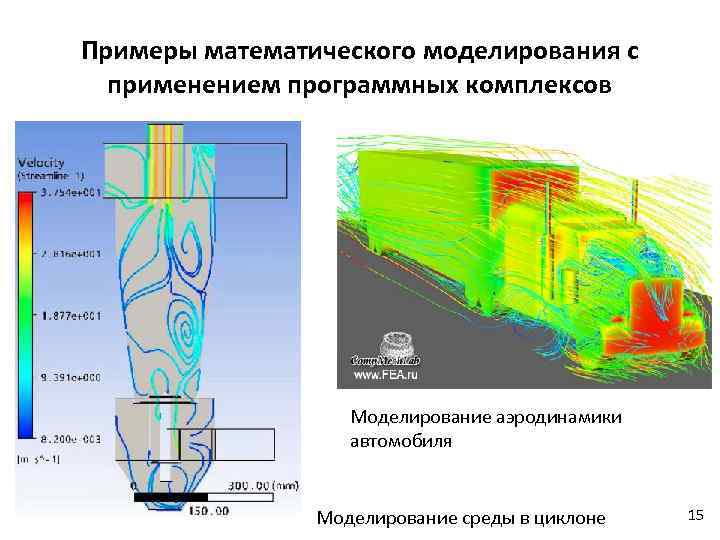 Примеры математического моделирования с применением программных комплексов Моделирование аэродинамики автомобиля Моделирование среды в циклоне 15
Примеры математического моделирования с применением программных комплексов Моделирование аэродинамики автомобиля Моделирование среды в циклоне 15
 16
16
 Темы рефератов 1. Пакеты прикладных программ компьютерного моделирования гидродинамики. Обзор и сравнение. 2. Пакеты для построения расчетных сеток. Обзор и сравнение. 3. Численные методы решения уравнений гидродинамики. Метод конечных разностей. 4. Численные методы решения уравнений гидродинамики. Метод конечных элементов. 5. Численные методы решения уравнений гидродинамики. Метод контрольных (конечных) объёмов. 6. Численные методы решения уравнений гидродинамики. Метод сглаженных частиц. 7. Численные методы решения уравнений гидродинамики. Метод с использованием функции распределения вероятности. 8. Обзор методов расчета турбулентных течений – DNS и LES (Large eddy simulation) методы. 9. Модель турбулентности k-ε (суть, границы применимости, достоинства и недостатки). 10. Модель турбулентности k-ω. 11 -12. Модели турбулентности Рейнольдсовых напряжений Reynolds Stress Models (SSG Reynolds Stress, LRR Reynolds Stress и др. ). Реферат + выступление с докладом и презентацией на 15 -20 мин. 17
Темы рефератов 1. Пакеты прикладных программ компьютерного моделирования гидродинамики. Обзор и сравнение. 2. Пакеты для построения расчетных сеток. Обзор и сравнение. 3. Численные методы решения уравнений гидродинамики. Метод конечных разностей. 4. Численные методы решения уравнений гидродинамики. Метод конечных элементов. 5. Численные методы решения уравнений гидродинамики. Метод контрольных (конечных) объёмов. 6. Численные методы решения уравнений гидродинамики. Метод сглаженных частиц. 7. Численные методы решения уравнений гидродинамики. Метод с использованием функции распределения вероятности. 8. Обзор методов расчета турбулентных течений – DNS и LES (Large eddy simulation) методы. 9. Модель турбулентности k-ε (суть, границы применимости, достоинства и недостатки). 10. Модель турбулентности k-ω. 11 -12. Модели турбулентности Рейнольдсовых напряжений Reynolds Stress Models (SSG Reynolds Stress, LRR Reynolds Stress и др. ). Реферат + выступление с докладом и презентацией на 15 -20 мин. 17


