МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ 1 ИНЖЕНЕРНЫЕ ЗАДАЧИ И МЕТОДОЛОГИЯ

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ • 1. ИНЖЕНЕРНЫЕ ЗАДАЧИ И МЕТОДОЛОГИЯ ВЫЧИСЛИТЕЛЬНОГО ЭКСПЕРИМЕНТАЛЬНЫЕ ФАКТОРНЫЕ МОДЕЛИ. • 2. КЛАССИФИКАЦИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ. ЭТАПЫ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ. • 3. ВЫЧИСЛИТЕЛЬНЫЕ АЛГОРИТМЫ И ПОГРЕШНОСТИ ВЫЧИСЛЕНИЙ. ОСНОВНЫЕ ПОНЯТИЯ. • 4 - 5. АНАЛИЗ ФАКТОРНОЙ МОДЕЛИ ТЕХНИЧЕСКОГО ОБЪЕКТА. АНАЛИТИЧЕСКОЕ И ЧИСЛЕННОЕ РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ. • 6. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ТЕХНИЧЕСКОГО ОБЪЕКТА НА МАКРОУРОВНЕ. ДИНАМИЧЕСКИЕ СИСТЕМЫ С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ. • 7. МОДЕЛИРОВАНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ТЕХНИЧЕСКИХ СИСТЕМАХ. ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ. • 8 - 9. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ТИПОВЫХ ЭЛЕМЕНТОВ ТЕХНИЧЕСКИХ СИСТЕМ НА МИКРОУРОВНЕ И ЧИСЛЕННЫЕ МЕТОДЫ ИХ АНАЛИЗА.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ИНЖЕНЕРНЫЕ ЗАДАЧИ И МЕТОДОЛОГИЯ ВЫЧИСЛИТЕЛЬНОГО ЭКСПЕРИМЕНТАЛЬНЫЕ ФАКТОРНЫЕ МОДЕЛИ. • • Вычислительный эксперимент (основные этапы решения сложных инженерных задач). Классификация математических моделей технических объектов. Примеры математических моделей. Основные типы задач (прямые задачи, обратные задачи, задачи идентификации). Модель черного ящика. Экспериментальные факторные модели (регрессионные модели технических объектов). Оценка параметров регрессионной модели по методу наименьших квадратов. Полиномиальные модели; определение оптимальной степени полинома.

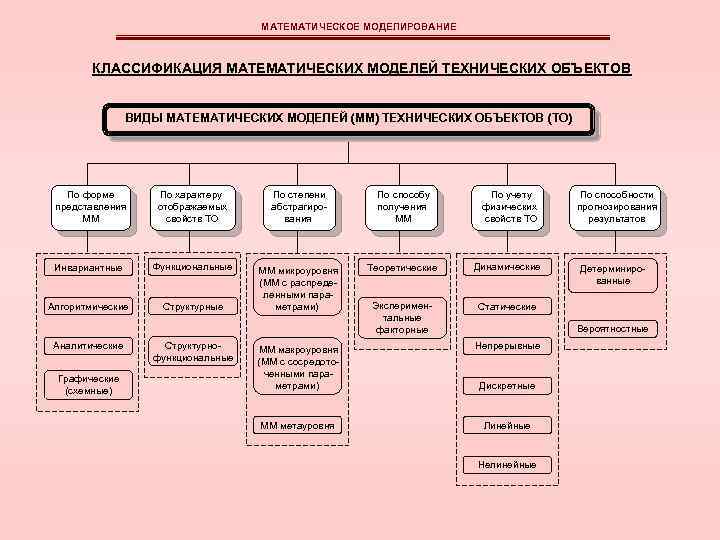МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ КЛАССИФИКАЦИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ТЕХНИЧЕСКИХ ОБЪЕКТОВ ВИДЫ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ (ММ) ТЕХНИЧЕСКИХ ОБЪЕКТОВ (ТО) По форме представления ММ По характеру отображаемых свойств ТО По степени абстрагирования По способу получения ММ По учету физических свойств ТО Инвариантные Функциональные Теоретические Динамические Алгоритмические Структурные ММ микроуровня (ММ с распределенными параметрами) Экспериментальные факторные Статические Аналитические Графические (схемные) Структурнофункциональные По способности прогнозирования результатов Детерминированные Вероятностные ММ макроуровня (ММ с сосредоточенными параметрами) Непрерывные ММ метауровня Линейные Дискретные Нелинейные

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ОСНОВНЫЕ ЭТАПЫ РЕШЕНИЯ СЛОЖНЫХ ИНЖЕНЕРНЫХ ЗАДАЧ. Решение сложной прикладной задачи с использованием вычислительной техники можно разбить на ряд последовательных этапов: • • • 1) постановка проблемы; определение целей моделирования; формулировка технического задания на разработку модели; 2) построение математической модели; 3) постановка вычислительной задачи; 4) предварительный анализ задачи; 5) выбор (или разработка) численного метода решения; 6) разработка вычислительного алгоритма и программирование; 7) отладка и тестирование компьютерной программы; 8) проведение расчетов и обработка их результатов; 9) проверка адекватности модели; если необходимо, уточнение математической модели и переход к п. 3); 10) выработка определенных практических рекомендаций. Вычислительный эксперимент – новая технология научных и прикладных исследований

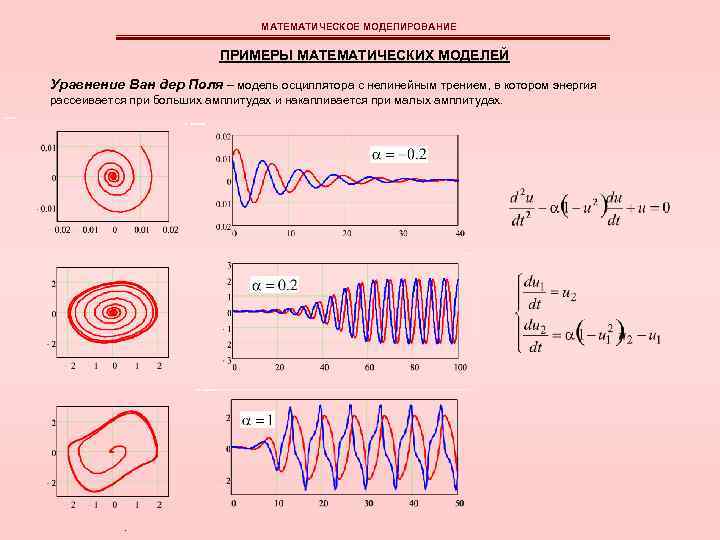МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРИМЕРЫ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ Уравнение Ван дер Поля – модель осциллятора с нелинейным трением, в котором энергия рассеивается при больших амплитудах и накапливается при малых амплитудах.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРИМЕРЫ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ Система Лоренца

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРИМЕРЫ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ Уравнения математической физики : – уравнение Лапласа – уравнение Пуассона – волновое уравнение – уравнение теплопроводности

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ УНИВЕРСАЛЬНОСТЬ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ Одна и та же математическая модель находит подчас самые различные приложения. Например, с помощью модели, содержащей уравнение Пуассона • • можно изучать - установившееся течение (несжимаемой) жидкости; - стационарные тепловые поля; - распределение электрического потенциала; - механические напряжения при кручении стержней; - деформацию тонкой мембраны; - фильтрацию нефти в нефтеносном пласте или влаги в почве; - диффузию посторонней примеси в твердом теле, жидкости или газе; - распространение эпидемии в регионе. В каждой из перечисленных задач функции и приобретают свой содержательный смысл, однако их связь описывается общим для всех задач уравнением Пуассона.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРИМЕРЫ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ Законы сохранения для индивидуального объема сплошной среды в интегральной форме: • масса объема неизменна, т. е. производная по времени от массы движущегося объема равна нулю • импульс изменяется за счет приложенных сил (объемных и поверхностных); его производная по времени равна сумме (главному вектору) всех сил, приложенных к объему : • энергия изменяется за счет работы внешних сил (объемных и поверхностных) и дополнительного притока энергии немеханического происхождения (за счет теплопроводности, электромагнитных явлений, фазовых переходов, химических превращений); ее производная по времени равна мощности, развиваемой действующими силами, плюс скорость притока дополнительной энергии

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРИМЕРЫ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ • Законы сохранения в дифференциальной форме : закон сохранения массы или уравнение неразрывности • закон сохранения импульса (количества движения) или уравнение движения • закон сохранения энергии или первый закон термодинамики

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРИМЕРЫ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ. УРАВНЕНИЯ НАВЬЕ – СТОКСА. • Математическая модель однородной изотропной несжимаемой линейно-вязкой жидкости – это система четырех уравнений относительно четырех неизвестных функций • Развернутая запись системы уравнений в декартовой системе координат:

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ОСНОВНЫЕ ТИПЫ ИНЖЕНЕРНЫХ И НАУЧНО-ТЕХНИЧЕСКИХ ЗАДАЧ. • Предположим, что математическая модель (ММ) исследуемого объекта (процесса, явления, системы), может быть представлена в виде соотношения где – символическая запись некоторого математического оператора (например, системы алгебраических или дифференциальных уравнений), который переменным ставит в соответствие переменную. • • Все величины, входящие в математическую модель, условно разбиваются на три группы: - исходные (или входные) данные , - параметры модели , - выходные данные (или искомое решение). В инженерной практике встречаются три типа задач: прямые задачи, обратные задачи идентификации. (Здесь они расположены в порядке возрастания сложности задач).

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРЯМЫЕ ЗАДАЧИ. • • Среди разных типов задач чаще всего приходится иметь дело с прямыми задачами. Постановка прямых задач выглядит следующим образом: по заданным значениям входных данных при фиксированных значениях параметров требуется найти решение (выходные данные) : параметры (заданы) «следствия» (выясняются в процессе моделирования) «причины» (известны) • Процесс решения прямой задачи можно рассматривать как поиск (математическое моделирование) причинно-следственной связи, присущей исследуемому явлению. Тогда входные данные характеризуют причины, а выходные – следствие. Решение прямой задачи призвано ответить на вопрос: «что будет, если реализуется определенный комплекс исходных условий» ? Варьируя входные данные, мы получаем определенный ответ на этот вопрос.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ОБРАТНЫЕ ЗАДАЧИ ИДЕНТИФИКАЦИИ. • • Постановка обратных задач: по заданным значениям выходных данных и фиксированных значениях параметров требуется найти значения входных данных. Решение обратной задачи – это в известном смысле попытка выяснить, какие причины привели (могут привести) к известному следствию. Как правило, обратные задачи существенно сложнее прямых задач и относятся к классу некорректных задач. Задача идентификации модели, понимаемая в широком смысле, - это задача выбора среди множества всевозможных моделей той, которая наиболее адекватно (полно, наилучшим образом) описывает изучаемый объект (проблему, явление). Обычно задачу идентификации понимают в узком смысле, как задачу выбора параметров модели таким образом, чтобы причины и следствия (т. е. входные и выходные данные) согласовывались друг с другом наилучшим образом.

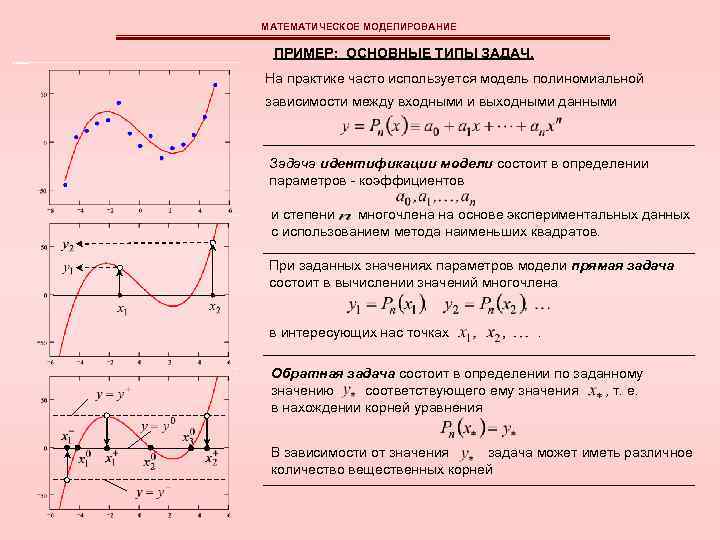МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРИМЕР: ОСНОВНЫЕ ТИПЫ ЗАДАЧ. На практике часто используется модель полиномиальной зависимости между входными и выходными данными Задача идентификации модели состоит в определении параметров - коэффициентов и степени многочлена на основе экспериментальных данных с использованием метода наименьших квадратов. При заданных значениях параметров модели прямая задача состоит в вычислении значений многочлена в интересующих нас точках . Обратная задача состоит в определении по заданному значению соответствующего ему значения , т. е. в нахождении корней уравнения В зависимости от значения задача может иметь различное количество вещественных корней

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ МОДЕЛЬ «ЧЕРНОГО ЯЩИКА» Объект исследования Модель «черного ящика» отображает только связи системы со средой, в виде перечня «входов» и «выходов» . В этой модели отсутствуют (или не используются в явной форме) сведения о внутреннем содержании «ящика» . Модель «черного ящика» используется на самых ранних этапах исследования нового объекта или когда ММ объекта настолько сложна, что не может быть непосредственно использована при оптимизации. Переменные величины, входящие в модель: • входные переменные (внутренние и внешние параметры объекта) - контролируемые (измеряемые) переменные, - контролируемые и управляемые переменные, - контролируемые, но неуправляемые переменные; эти переменные называются факторами; пространство контролируемых переменных образует факторное пространство; • выходные переменные (показатели качества и эффективности) - отклик объекта; зависимость величины от входных переменных называется функцией отклика; геометрическое представление функции отклика в факторном пространстве называют поверхностью отклика; • помехи (случайные и/или систематические ошибки) помехи – это неконтролируемые и неуправляемые переменные; они могут быть обусловлены неточностью физического (или математического) моделирования исследуемого объекта, ошибками измерительных приборов, неконтролируемыми изменениями параметров объекта и внешней среды и т. п.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКСПЕРИМЕНТАЛЬНАЯ ФАКТОРНАЯ МОДЕЛЬ (ЭФМ) • • Теоретические модели технических систем имеют то преимущество, что они непосредственно базируются на физических законах, описывающих происходящие в исследуемом объекте процессы. Иногда они чрезмерно сложны, тогда используются экспериментальные модели. Экспериментальные факторные модели (ЭФМ), в отличие от теоретических, не используют физических законов, а представляют собой некоторые формальные зависимости выходных параметров от внутренних и внешних параметров объекта моделирования. ЭФМ может быть построена на основе физических или вычислительных экспериментов. Физические эксперименты проводятся непосредственно на самом техническом объекте (при создании новых объектов эксперимент проводится на прототипах и аналогах, а иногда на макетных образцах). В вычислительных экспериментах исследование ведется на математической модели объекта-оригинала. Для построения экспериментальной факторной модели необходимо определить ее структуру. Под структурой факторной модели понимается вид математических соотношений, связывающих отклик с факторами. Структуру модели обычно выбирают на основе анализа априорной информации об объекте, учитывая при этом характер ее последующего использования. При отсутствии априорной информации рассматривают полиномиальные факторные модели. Неизвестные коэффициенты уравнений факторной модели называются параметрами модели; процедура их вычисления (называемая анализом регрессии) полностью формализована и сводится к применению метода наименьших квадратов. ЭФМ называют также регрессионными моделями.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРИМЕРЫ ФАКТОРНЫХ МОДЕЛЕЙ Структура линейной однофакторной и линейной трехфакторной модели Линейные эффекты Структура нелинейной двухфакторной модели Нелинейные эффекты Структура полиномиальной модели, включающей факторов Эффекты парного взаимодействия Эффекты тройного взаимодействия • Регрессионный анализ включает три основных этапа: - предварительный статистический анализ результатов эксперимента (исключение грубых ошибок, проверка статистических гипотез о законе распределения результатов измерений и однородности дисперсий, оценка дисперсии воспроизводимости эксперимента); - вычисление коэффициентов регрессионной модели и проверка их статистической значимости; - оценка адекватности и работоспособности полученной модели.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ОДНОФАКТОРНАЯ ЭКСПЕРИМЕНТАЛЬНАЯ МОДЕЛЬ. • Рассмотрим однофакторную экспериментальную модель. Уравнение регрессии, устанавливающее зависимость между оценкой условного математического ожидания функции отклика и фактором имеет в общем случае вид: где - параметры факторной модели, при данном значении фактора. • • , - среднее значение отклика Пусть в интересующей нас области факторного пространства выбраны значений (уровней) фактора , и пусть в результате физического или вычислительного эксперимента получены соответствующие значения отклика системы. Задача состоит в том, чтобы на основе полученной таблицы экспериментальных значений вычислить параметры модели. В общем случае линейной зависимости функции от искомых параметров она представляется в виде так называемого обобщенного многочлена где заданная система базисных функций. Базисные функции алгебраических многочленов:

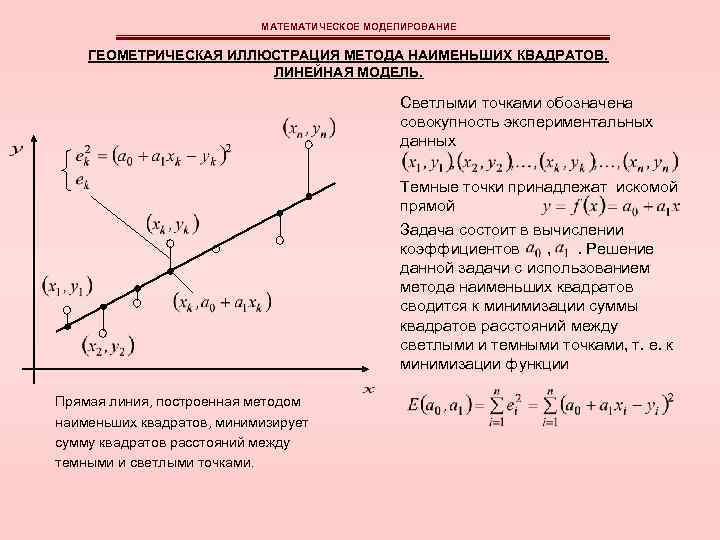МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ГЕОМЕТРИЧЕСКАЯ ИЛЛЮСТРАЦИЯ МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ. ЛИНЕЙНАЯ МОДЕЛЬ. Светлыми точками обозначена совокупность экспериментальных данных Темные точки принадлежат искомой прямой Задача состоит в вычислении коэффициентов , . Решение данной задачи с использованием метода наименьших квадратов сводится к минимизации суммы квадратов расстояний между светлыми и темными точками, т. е. к минимизации функции Прямая линия, построенная методом наименьших квадратов, минимизирует сумму квадратов расстояний между темными и светлыми точками.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЛИНЕЙНАЯ МОДЕЛЬ. ВЫВОД НОРМАЛЬНЫХ УРАВНЕНИЙ. • Линейная функция Вычисление коэффициентов методом наименьших квадратов сводится к минимизации суммы квадратов невязок: Вычисляя частные производные , и приравнивая их нулю, получим систему двух линейных уравнений Решение этой системы имеет вид:

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЛИНЕЙНАЯ МОДЕЛЬ. МАТРИЧНЫЙ ВЫВОД НОРМАЛЬНЫХ УРАВНЕНИЙ. • • , Линейная функция Система условных уравнений • Произведение матриц • Нормальная система уравнений Матричная форма записи

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ КВАДРАТИЧНАЯ МОДЕЛЬ. НОРМАЛЬНЕ УРАВНЕНИЯ. • Полином второй степени • Система условных уравнений • Матричная форма записи • Нормальная система уравнений

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПОЛИНОМ ПРОИЗВОЛЬНОЙ СТЕПЕНИ. НОРМАЛЬНЫЕ УРАВНЕНИЯ. : • Полином степени • Система условных уравнений • Матричная форма записи исходных уравнений • Система нормальных уравнений

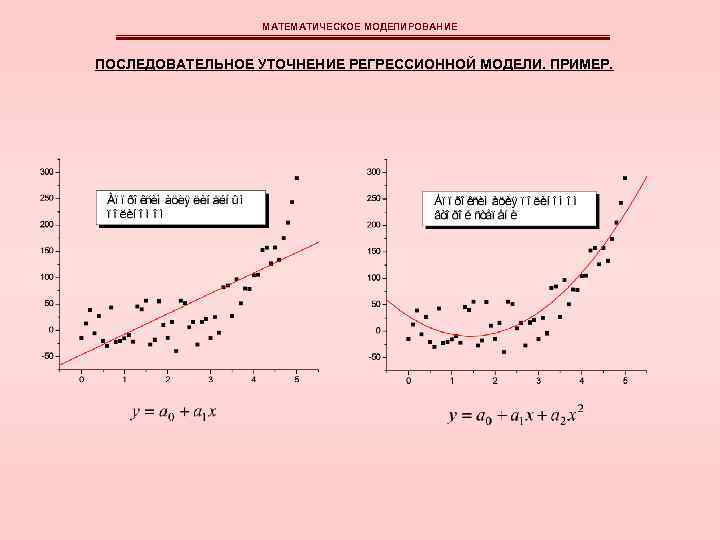МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПОСЛЕДОВАТЕЛЬНОЕ УТОЧНЕНИЕ РЕГРЕССИОННОЙ МОДЕЛИ. ПРИМЕР.

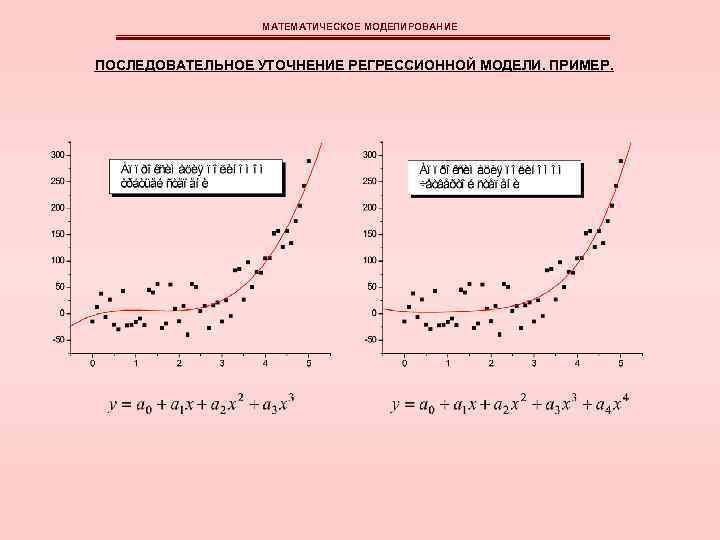МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПОСЛЕДОВАТЕЛЬНОЕ УТОЧНЕНИЕ РЕГРЕССИОННОЙ МОДЕЛИ. ПРИМЕР.

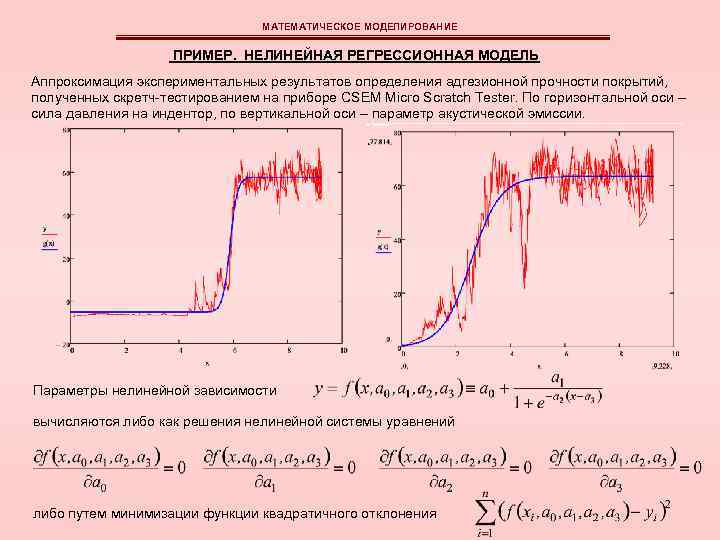МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРИМЕР. НЕЛИНЕЙНАЯ РЕГРЕССИОННАЯ МОДЕЛЬ Аппроксимация экспериментальных результатов определения адгезионной прочности покрытий, полученных скретч-тестированием на приборе CSEM Micro Scratch Tester. По горизонтальной оси – сила давления на индентор, по вертикальной оси – параметр акустической эмиссии. Параметры нелинейной зависимости вычисляются либо как решения нелинейной системы уравнений либо путем минимизации функции квадратичного отклонения

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ? ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ. • • • 1. Что такое вычислительный эксперимент? 2. Основные типы инженерных и научно-технических задач. Приведите определения и дайте характеристику типов задач, укажите соответствующие примеры 3. Приведите примеры математических моделей, описываемых конечными соотношениями. 4. Приведите примеры математических моделей, описываемых обыкновенными дифференциальными уравнениями. 5. Приведите примеры математических моделей, описываемых дифференциальными уравнениями в частных производных. 6. Перечислите этапы решения научно-технических задач; дайте краткую характеристику каждому этапу. 7. Что такое модель «черного ящика» ? В чем трудность построения этой модели, в чем ее недостатки? Когда на практике применяется модель «черного ящика» ? 8. Как строятся экспериментальные факторные модели? Что понимается под структурой этих моделей, в чем состоит задача идентификации моделей? Приведите примеры. 9. В чем суть метода наименьших квадратов? Когда он используется? Проиллюстрируйте сказанное графически (на примере линейной или нелинейной однофакторной модели). 10. Как получается нормальная система уравнений? 11. Приведите вывод нормальных уравнений для квадратичной однофакторной модели. Как решается полученная система уравнений? Литература: [3], [1], [2], [5]

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ • • ЛИТЕРАТУРА ОСНОВНАЯ 1. Амосов А. А. , Дубинский Ю. А. , Копченова Н. В. Вычислительные методы для инженеров. – М. : Высшая школа, 1994. 2. Введение в математическое моделирование / Под ред. П. В. Трусова. - М. : Интермет Инжиниринг, 2000. 3. Тарасик В. П. Математическое моделирование технических систем. - Минск. : Дизайн. ПРО, 2004. 4. Самарский А. А. , Михайлов А. П. Математическое моделирование: Идеи. Методы. Примеры. – М. : Наука, 2002. 5. Тихонов А. Н. , Костомаров Д. П. Вводные лекции по прикладной математике. – М. : Наука, 1984. 6. Тихонов А. Н. , Самарский А. А. Уравнения математической физики. – М. : Наука, 1966. 7. Ивановский Р. И. Компьютерные технологии в науке и образовании. Практика применения систем Math. CAD PRO, - М. : Высшая школа, 2003. ЛИТЕРАТУРА ДОПОЛНИТЕЛЬНАЯ • • 8. Зарубин В. С. Математическое моделирование в технике. – М. : Изд-во МГТУ им. Н. Э. Баумана, 2003. 9. Бордовский Г. А. , Кондратьев А. С. , Чоудери А. Д. Р. Физические основы математического моделирования. – М. : Издательский центр «Академия» , 2005. 10. Форсайт Дж. , Малькольм М. , Моулер К. Машинные методы математических вычислений. – М. : Мир, 1980. 11. Калиткин Н. Н. Численные методы. - М. : Наука, 1978. 12. Турчак Л. И. , Плотников. Основы численных методов. – М. : Физматлит, 2005. 13. Самарский А. А. , Гулин А. В. Численные методы. – М. : Наука, 1989. 14. Фарлоу С. Уравнения с частными производными для научных работников и инженеров. – М. : Мир, 1985. 15. Плис А. И. , Сливина Н. А. Mathcad 2000. Математический практикум для экономистов и инженеров. – М. : Финансы и статистика, 2000.