Математическое и численное моделирование течения флюида в

«Математическое и численное моделирование течения флюида в ступени центробежного насоса» Научный руководитель темы: проф. , д. ф. -м. н. Ф. А. Слободкина Кафедра нефтегазовой и подземной гидромеханики РГУ нефти и газа им. И. М. Губкина 1

Актуальность работы n n n Использование лопаточных машин во многих отраслях науки и техники обусловило бурное развитие этой области не только применительно к системам водоснабжения, канализации, но и к авиационной и нефтяной промышленности. В 60 – 70 е гг. бурно развивается теория лопаточных машин, применяемых в аэродинамике – турбин и компрессоров Большой вклад в изучение работы погружных центробежных насосов, используемых в нефтяной промышленности, внесли Г. Ф. Проскура, А. А. Ломакин, С. С. Руднев, В. С. Квятковский, И. Г. Есьман, Н. М. Щапов, Н. Н. Вознесенский, И. И. Куколевский, Т. М. Башта, Р. И. Кривченко, В. М. Касьянов, П. Д. Ляпков, Н. Н. Репин, И. Т. Мищенко и др. 2

Актуальность работы n n n Широкое распространение получили экспериментальные методы исследования и эмпирические теории расчетов. Для приближенных расчетов характеристик насосов используют аналитический метод расчета, основанный на законах сохранения массы и кол-ва движения, но не учитывающий вязкость, сжимаемость флюида, а также турбулентность течения Практическая направленность работы: необходимость учета и объяснения возникающих в ступени потерь и прогнозирования возможных проблем при различных режимах эксплуатации насоса применительно к нефтяной промышленности. 3

Цель работы n Построение математической модели, описывающей течение флюида в ступени центробежного насоса Основные задачи исследования При построении математической модели течения флюида : n n n учесть вязкость и сжимаемость перекачиваемого флюида, турбулентность потока; учесть потери на трение и вихреобразование в элементах ротора и статора ступени насоса; получить в общем виде систему дифференциальных уравнений для описания течения сжимаемой вязкой жидкости в ступени ЦН. На основе численных реализаций построенной математической модели : получить распределения параметров потока в межлопастных каналах рабочего колеса и направляющего устройства для диапазона подач 30 – 160 м 3/сут; используя полученные распределения, сравнить теоретические и экспериментальные данные; используя полученные распределения параметров потока, проанализировать возникающие в элементах ступени центробежного насоса потери и оценить возможность их уменьшения. 4

Научная новизна (1) 1. В общем виде выписана система дифференциальных уравнений, описывающая течение вязкой сжимаемой жидкости с учетом турбулентности в ступени центробежного насоса. 2. Дано решение задач для случая течения воды и дегазированной нефти в ступени центробежного насоса ЦУНАР 80. 3. Показано, что в случае больших величин объемных расходов основные потери идут на вихреобразование, вызванное инжекцией высокоскоростной струи в полость статора, а в случае малых объемных расходов потери связаны с возникновением большого количества малых вихрей во входном канале полости диффузора. 5

Научная новизна (2) 4. Показано, что особенности геометрии входного канала полости статора неминуемо приводят к его запиранию при малых значениях объемного расхода; особенности геометрии полости диффузора приводят к возникновению системы присоединенных вихрей, занимающих большую часть объема полости и существенно уменьшающих площадь проходного сечения. 5. Показано, что с увеличением вязкости перекачиваемого флюида: высота напора и коэффициент полезного действия снижается; область оптимальных подач смещается в сторону меньших подач. Практическая ценность Повышение производительности центробежных насосов, используемых в нефтяной промышленности, в том числе совершенствование конструкции ступеней. 6

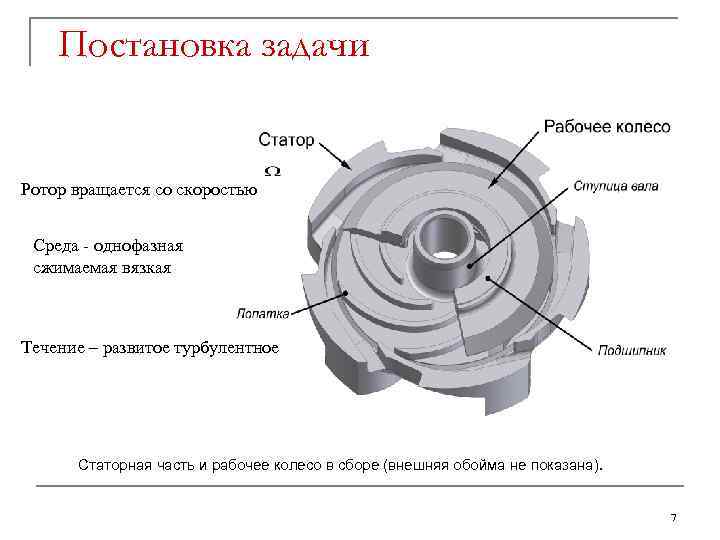Постановка задачи Ротор вращается со скоростью Среда - однофазная сжимаемая вязкая Течение – развитое турбулентное Статорная часть и рабочее колесо в сборе (внешняя обойма не показана). 7

Численное моделирование турбулентности Турбулентность - это "…завихреное течение с очень большим числом возбужденных степеней свободы и с хаотическим распределением дисперсионных соотношений и фазовых сдвигов”*. 1. Прямое численное моделирование. Численное решение системы алгебраических уравнений, с высокой точностью аппроксимирующих исходную систему дифференциальных уравнений Навье-Стокса, в каждой точке расчетной области 2. Моделирование методом крупных вихрей. Гипотеза: статистические характеристики крупномасштабных турбулентных движений не зависят от молекулярной вязкости. - Построение численной модели, описывающей динамику только относительно крупных вихрей (вносящих основной вклад в энергию турбулентного потока и определяющих взаимодействие турбулентности со средним движением). - Фильтрация мелкомасштабных пульсаций. - Результирующая система не замкнута, т. к. не включает описание нелинейных взаимодействий крупных вихрей с мелкомасштабной турбулентностью. * - Монин А. С. , А. М. Яглом. Статистическая гидромеханика. Часть 1. 8

Численное моделирование турбулентности 3. Решение систем уравнений, усредненных по Рейнольдсу. Статистический подход к исследованию турбулентности - осреднение уравнений движения по ансамблю состояний. Все параметры движения разлагаются на среднюю и турбулентную составляющие. Рассмотрим уравнения Навье-Стокса для несжимаемой вязкой среды. Входящие в них величины представляются в виде сумм средних полей и пульсаций. Подставив разложения и проведя осреднение, получим уравнения Рейнольдса где - тензор напряжений Рейнольдса 9

Численное моделирование турбулентности 3. Решение систем уравнений, усредненных по Рейнольдсу. Предположение: турбулентность образуется лишь в результате перехода части энергии осредненного течения в энергию мелкомасштабных возмущений. В этом случае все статистические характеристики турбулентности (в частности, напряжения Рейнольдса) должны зависеть от поля средней скорости - зависимость Буссинеска где - коэффициент турбулентной вязкости Предположение: турбулентная вязкость и энергия турбулентных пульсаций для данного течения есть величины постоянные. Существует достаточно большое количество моделей, дополняющих систему уравнений Рейнольдса необходимыми уравнениями с тензором напряжений Рейнольдса. В настоящей работе используется двухпараметрическая модель. 10

Методы исследования течения среды в ступени насоса. n Исходные уравнения, представляющие собой усреднённые по Рейнольдсу уравнения Навье-Стокса, записываются в дивергентной форме для цилиндрической системы координат (х, r, ), вращающейся с угловой скоростью ротора. n Среда предполагается однофазной сжимаемой вязкой, подчиняющейся двухпараметрическому уравнению состояния. n Течение – турбулентное. n При расчетах течения в не вращающихся областях проточной части насоса (элементов статоров, направляющих устройств и др. ) удобно использовать абсолютную цилиндрическую систему координат, а для вращающихся областей проточной части (элементов ротора) – относительную систему координат, вращающуюся с соответствующей угловой скоростью ротора. 11

Уравнения Навье-Стокса в трехмерной нестационарной постановке (1) В безразмерном виде система уравнений во вращающейся цилиндрической системе координат имеет вид: 12

Уравнения Навье-Стокса в трехмерной нестационарной постановке (2) В безразмерном виде система уравнений во вращающейся цилиндрической системе координат имеет вид: t – время, ρ – плотность, p – давление T – температура, S – энтропия, е* – внутренняя энергия, и , , –компоненты относительной скорости вдоль осей х, r и φ – коэффициенты молекулярной и турбулентной вязкости, и - числа Прандтля; Re - число Рейнольдса 13

Модель турбулентности В безразмерном виде система уравнений во вращающейся цилиндрической системе координат имеет вид: где - кинетическая энергия пульсаций 14

Модель турбулентности . Здесь расстояние вдоль нормали до стенки. Значения констант, входящих в последние формулы, следующие: 15

Начальные условия Начальными условиями задачи являются заданные в момент времени t=0 приближенные распределения гидродинамических параметров по всему рабочему пространству ступени насоса. Эти распределения могут вычисляться либо из решения одномерной задачи для моделируемого режима работы насоса, либо задаваться простейшим образом (например, полное отсутствие движения флюида в ступени в момент запуска насоса). Необходимым условием решения задачи является задание полной 3 D геометрии всей проточной части. 16

Граничные условия задачи: Граничные условия n n на неподвижных стенках все компоненты скорости задаются равными нулю – условие прилипания, на подвижных стенках скорость = , остальные компоненты скорости равны нулю; на входе в насос задаются полные параметры набегающего потока, а также направление скорости; на выходе - статическое давление окружающей среды. Другой вариант задания граничного условия на входе состоит в задании расхода флюида вместо полного давления. Такой подход дает более устойчивое решение, поэтому при проведении расчетов для надежности получаемых результатов моделировались параллельно два решения (на разных ПК) и проводилось их сравнение. 17

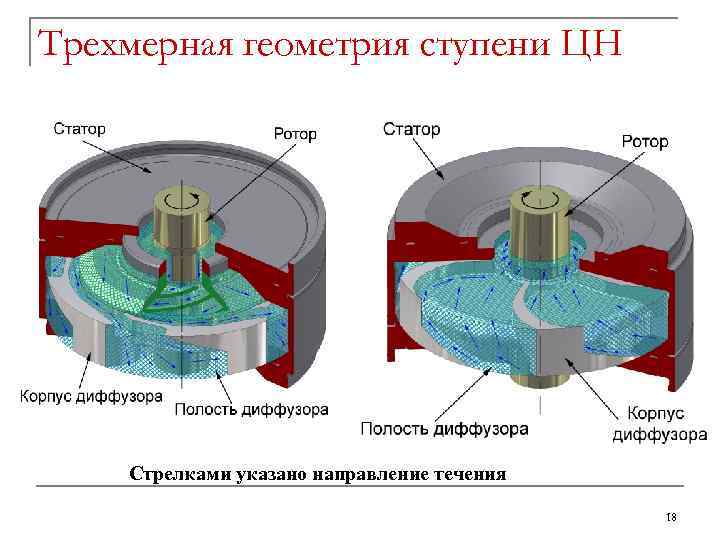Трехмерная геометрия ступени ЦН Стрелками указано направление течения 18

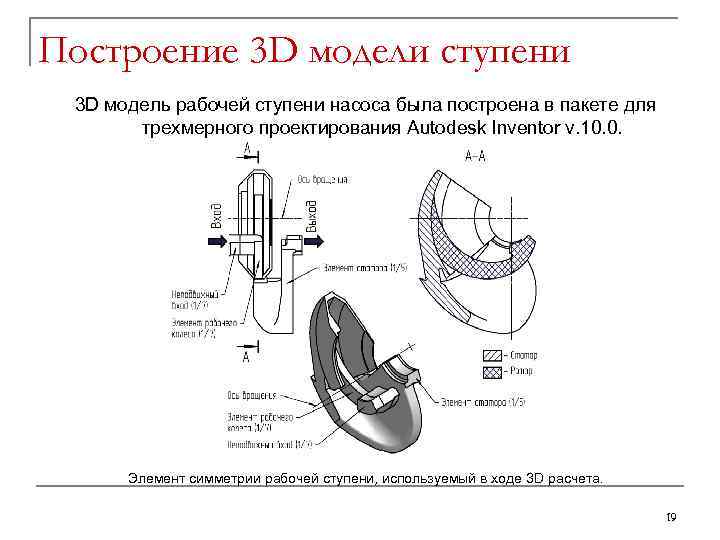Построение 3 D модели ступени 3 D модель рабочей ступени насоса была построена в пакете для трехмерного проектирования Autodesk Inventor v. 10. 0. Элемент симметрии рабочей ступени, используемый в ходе 3 D расчета. 19

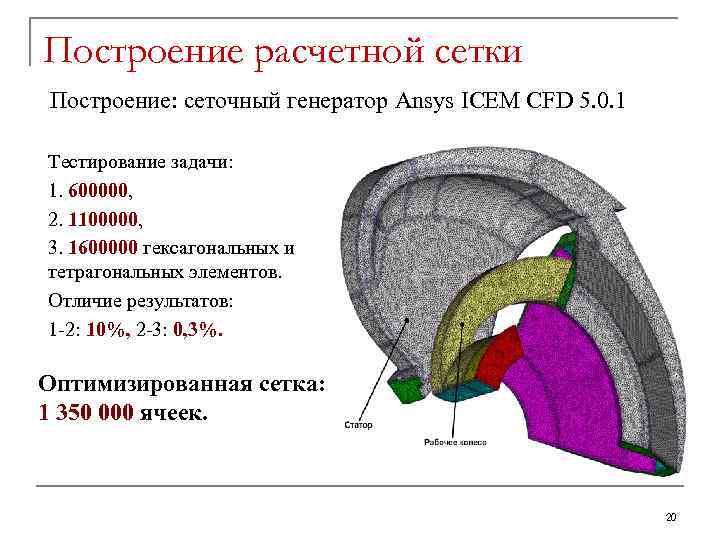Построение расчетной сетки Построение: сеточный генератор Ansys ICEM CFD 5. 0. 1 Тестирование задачи: 1. 600000, 2. 1100000, 3. 1600000 гексагональных и тетрагональных элементов. Отличие результатов: 1 -2: 10%, 2 -3: 0, 3%. Оптимизированная сетка: 1 350 000 ячеек. 20

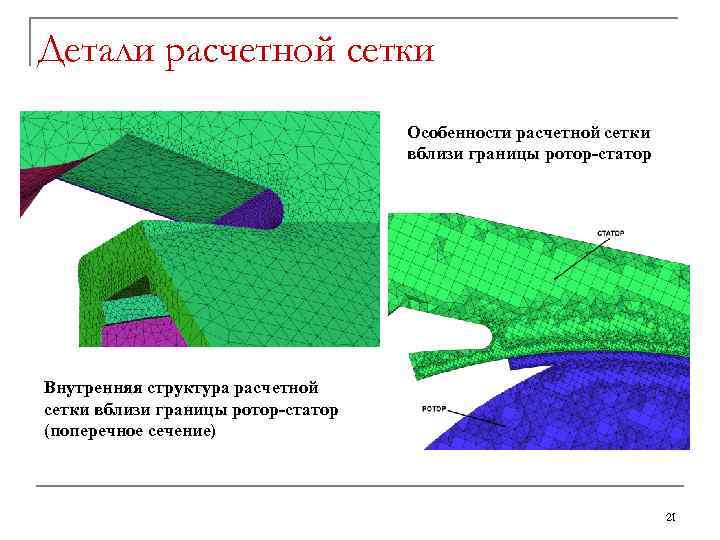Детали расчетной сетки Особенности расчетной сетки вблизи границы ротор-статор Внутренняя структура расчетной сетки вблизи границы ротор-статор (поперечное сечение) 21

Исходные данные Численный эксперимент проводился для ступени электроцентробежной погружной насосной установки для нефтедобычи - ЭЦН АКМ. Параметры расчета: ● Рабочее тело – вода : плотность ρ = 997 кг/м 3, вязкость m = 0. 001003 кг/м с, температура Т = 300 К. ● Рассматривается изотермический процесс. ● Частота вращения ротора насоса: ω = 10000 об/мин. В результате расчетов обнаружены существенные различия в характере течения при малых и больших расходах через ступень. В связи с этим анализ результатов будет приведен для двух предельных значений расходов, при которых проводился численный эксперимент: 30 м 3/сут и 160 м 3/сут. 22

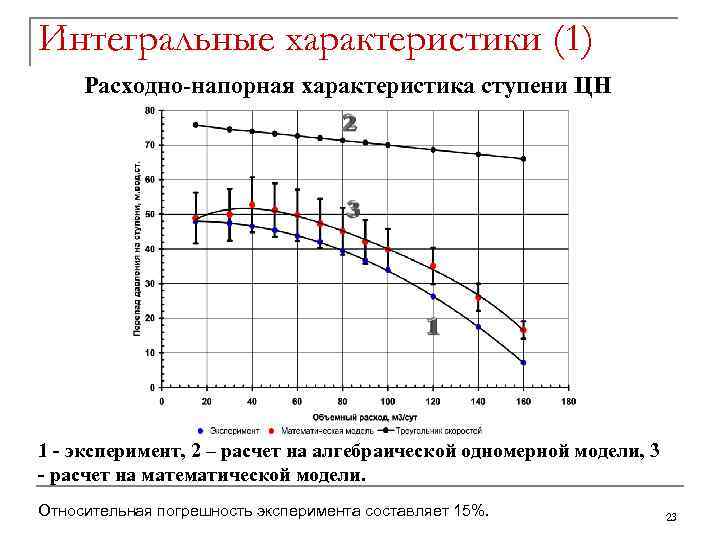Интегральные характеристики (1) Расходно-напорная характеристика ступени ЦН 1 - эксперимент, 2 – расчет на алгебраической одномерной модели, 3 - расчет на математической модели. Относительная погрешность эксперимента составляет 15%. 23

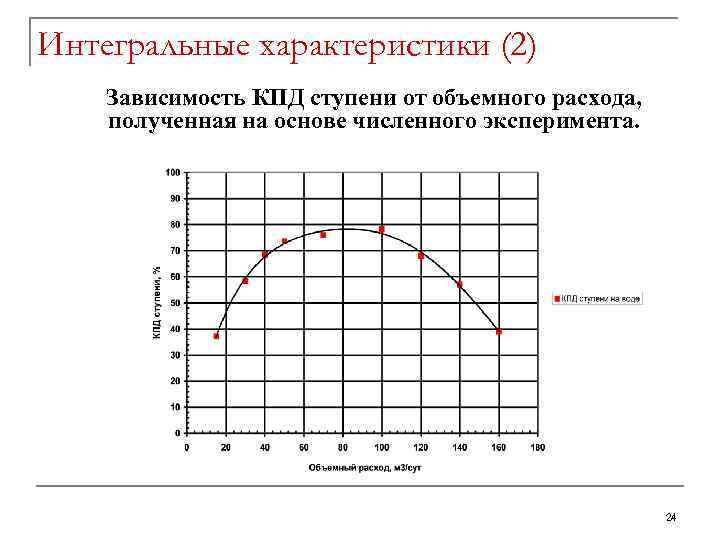Интегральные характеристики (2) Зависимость КПД ступени от объемного расхода, полученная на основе численного эксперимента. 24

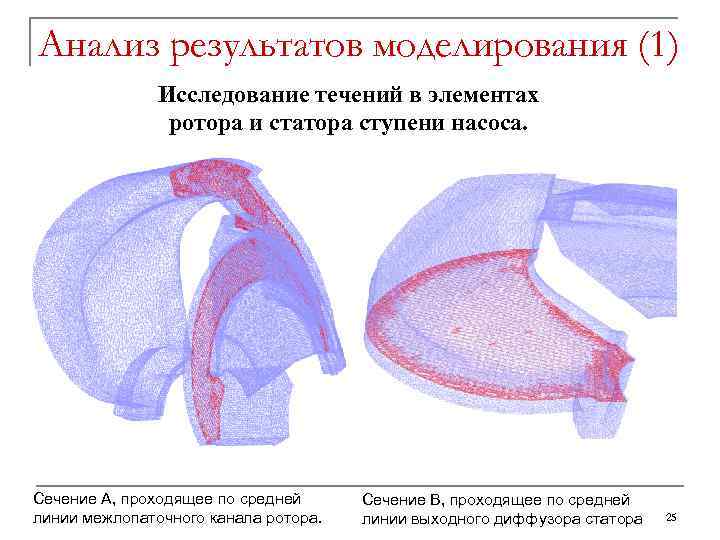Анализ результатов моделирования (1) Исследование течений в элементах ротора и статора ступени насоса. Сечение А, проходящее по средней линии межлопаточного канала ротора. Сечение В, проходящее по средней линии выходного диффузора статора 25

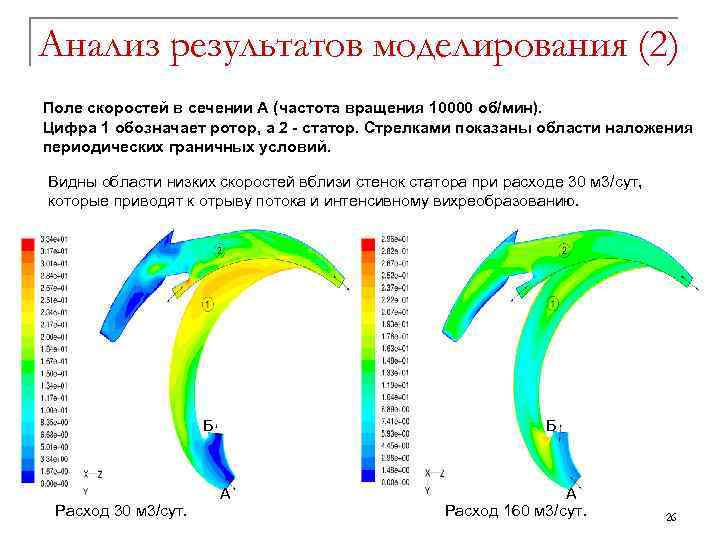Анализ результатов моделирования (2) Поле скоростей в сечении А (частота вращения 10000 об/мин). Цифра 1 обозначает ротор, а 2 - статор. Стрелками показаны области наложения периодических граничных условий. Видны области низких скоростей вблизи стенок статора при расходе 30 м 3/сут, которые приводят к отрыву потока и интенсивному вихреобразованию. Б Расход 30 м 3/сут. Б А А Расход 160 м 3/сут. 26

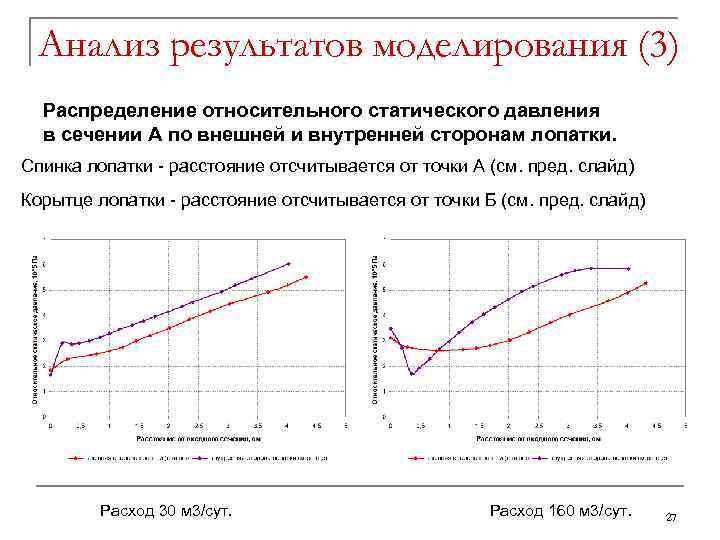Анализ результатов моделирования (3) Распределение относительного статического давления в сечении А по внешней и внутренней сторонам лопатки. Спинка лопатки - расстояние отсчитывается от точки А (см. пред. слайд) Корытце лопатки - расстояние отсчитывается от точки Б (см. пред. слайд) Расход 30 м 3/сут. Расход 160 м 3/сут. 27

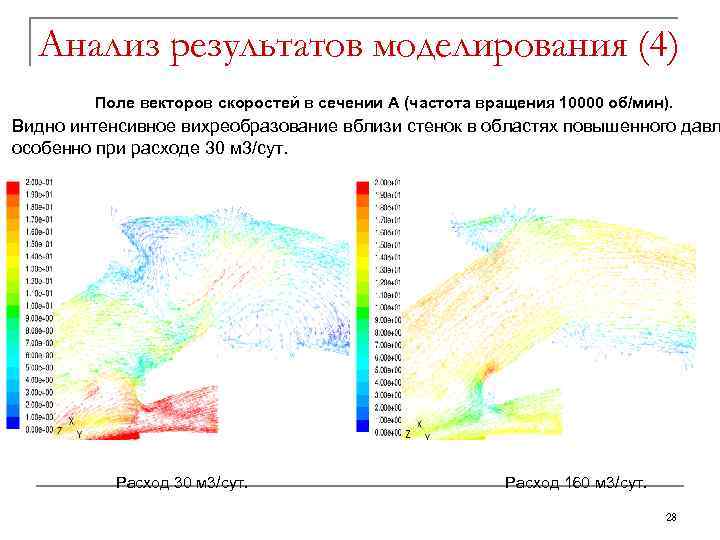Анализ результатов моделирования (4) Поле векторов скоростей в сечении А (частота вращения 10000 об/мин). Видно интенсивное вихреобразование вблизи стенок в областях повышенного давл особенно при расходе 30 м 3/сут. Объемный расход равен 30 м 3/сут Расход 30 м 3/сут. Объемный расход равен 160 м 3/сут Расход 160 м 3/сут. 28

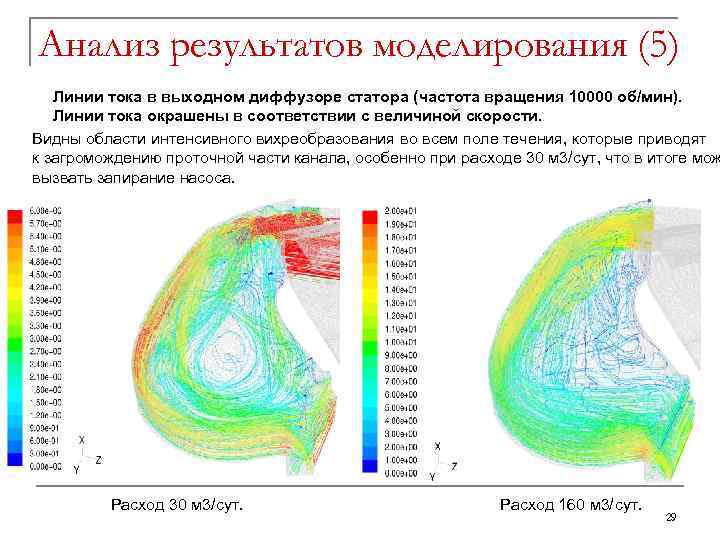Анализ результатов моделирования (5) Линии тока в выходном диффузоре статора (частота вращения 10000 об/мин). Линии тока окрашены в соответствии с величиной скорости. Видны области интенсивного вихреобразования во всем поле течения, которые приводят к загромождению проточной части канала, особенно при расходе 30 м 3/сут, что в итоге мож вызвать запирание насоса. Расход 30 м 3/сут. Расход 160 м 3/сут. 29

Анализ результатов моделирования (6) Рабочий агент: дегазированная нефть, плотность: 921 кг/м 3, сжимаемость: 1, 3*10 -3 1/МПа, вязкость: q q q 0. 005 Па*с, 0. 015 Па*с, 0. 025 Па*с. 30

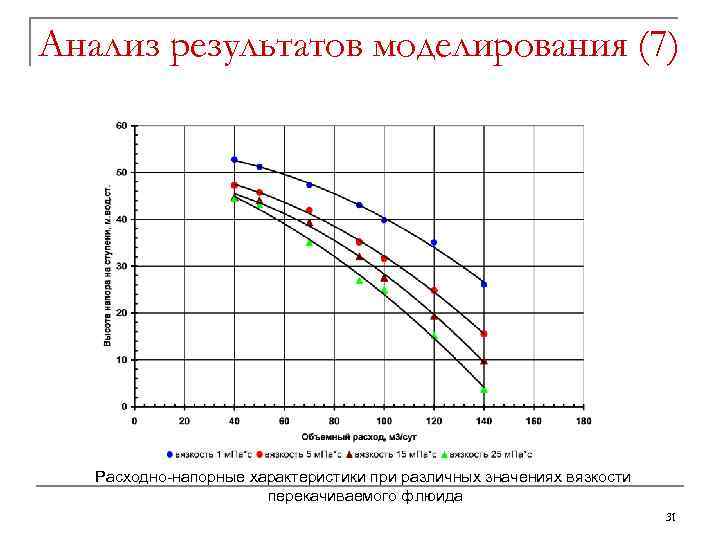Анализ результатов моделирования (7) Расходно-напорные характеристики при различных значениях вязкости перекачиваемого флюида 31

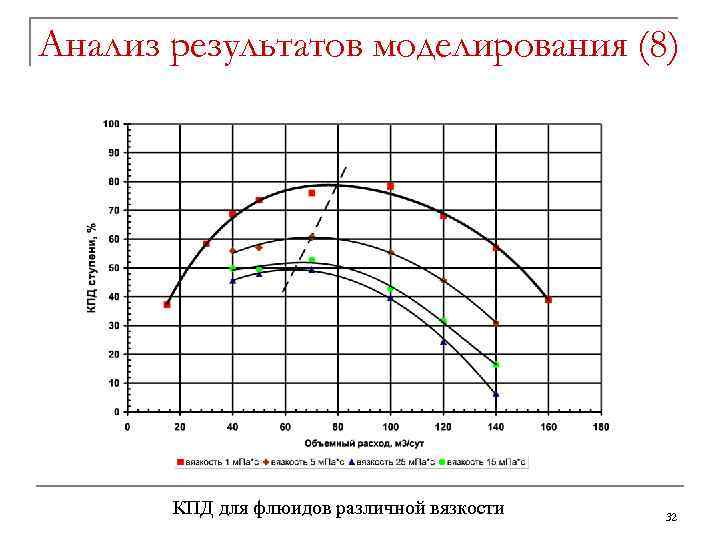Анализ результатов моделирования (8) КПД для флюидов различной вязкости 32

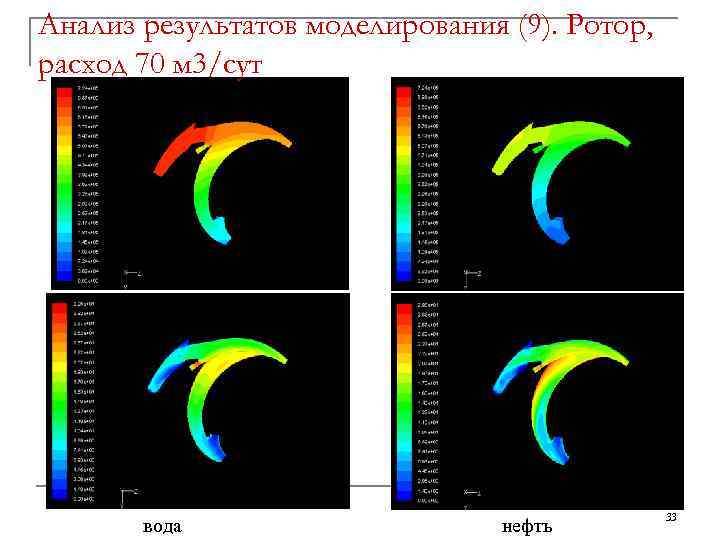Анализ результатов моделирования (9). Ротор, расход 70 м 3/сут вода нефть 33

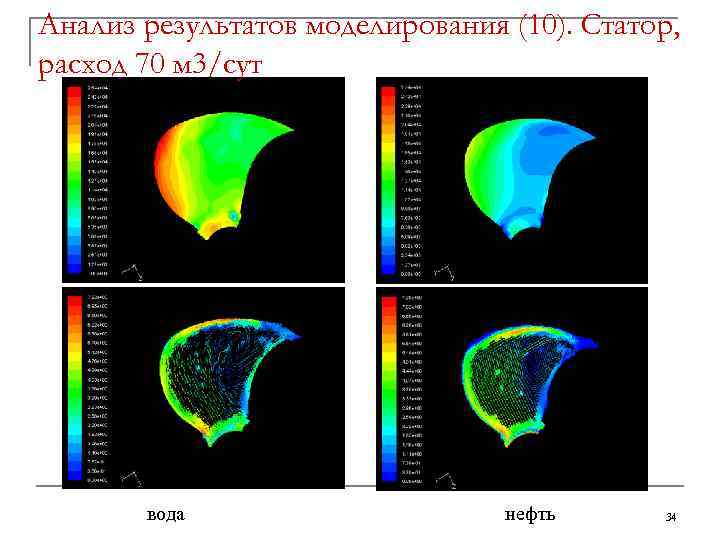Анализ результатов моделирования (10). Статор, расход 70 м 3/сут вода нефть 34

Выводы (1) 1. 2. 3. 4. Предложено математическое описание течения флюида, основанное на уравнениях Навье-Стокса с учетом вязкости флюида и развитой турбулентности потока. Разработан алгоритм решения полученной системы дифференциальных уравнений, который позволил улучшить сходимость численного процесса. Для проведения численных экспериментов создана твердотельная модель ступени насоса, который используется в нефтяной промышленности, . Сравнение интегральных характеристик ступени, полученных численными методами, с экспериментальными результатами продемонстрировало их хорошее согласование. 35

Выводы (2) 5. Проведенный анализ многовариантных расчетов течения флюида в диапазоне значений расходов 30 – 160 м 3/сут показал, что q в случае больших величин объемных расходов основные потери идут на вихреобразование, вызванное инжекцией высокоскоростной струи в полость статора, а в случае малых объемных расходов потери связаны с возникновением большого количества малых вихрей во входном канале полости диффузора; q особенности геометрии входного канала полости статора неминуемо приводят к его запиранию при малых значениях объемного расхода; q особенности геометрии полости диффузора приводят к возникновению системы присоединенных вихрей, занимающих большую часть объема полости и существенно уменьшающих площадь проходного сечения; q применив комплекс мер по перепрофилированию статорной части ступени центробежного насоса, можно существенно улучшить его гидродинамические характеристики и увеличить 36 эффективность работы насоса в целом. 6.

Выводы (3) 6. Проведен анализ зависимости течения флюида в ступени от вязкости в диапазоне значений 0. 001 – 0. 025 м. Па*с, который показал, что с увеличением вязкости: q высота напора уменьшается; q q коэффициент полезного действия снижается; область оптимальных подач смещается в область меньших расходов. 37