Математический формализм КМ НАЗНАЧЕНИЕ облегчение вычислений с участием

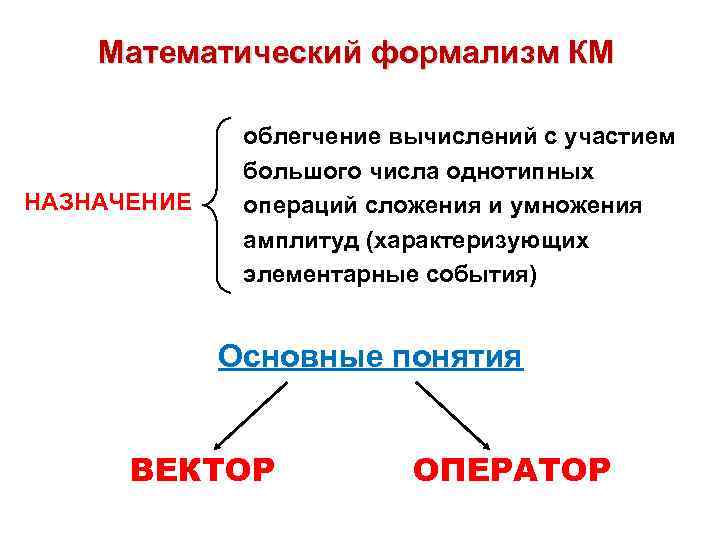
Математический формализм КМ НАЗНАЧЕНИЕ облегчение вычислений с участием большого числа однотипных операций сложения и умножения амплитуд (характеризующих элементарные события) Основные понятия ВЕКТОР ОПЕРАТОР

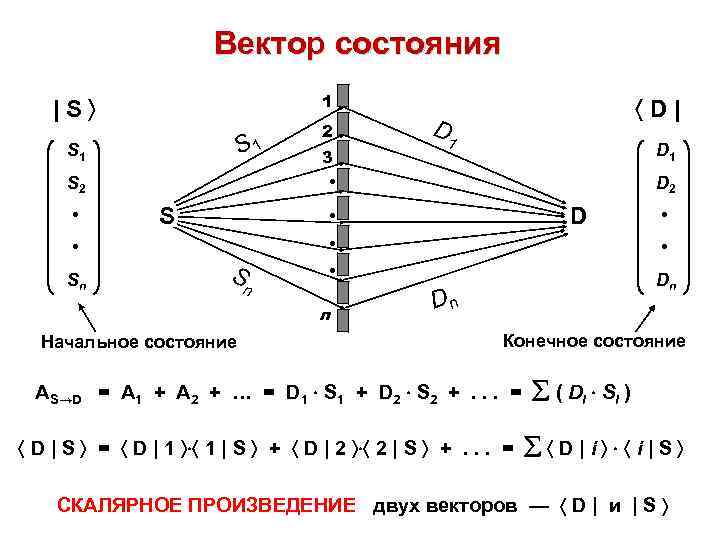
Вектор состояния 1 |S S 1 S 1 D 2 D • • • Sn 3 D • S 2 • 2 D| S n Начальное состояние • • n • Dn Dn Конечное состояние АS→D = А 1 + А 2 + … = D 1 S 1 + D 2 S 2 +. . . = D | S = D | 1 1 | S + D | 2 2 | S +. . . = ( Di S i ) D|i i|S СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ двух векторов — D | и | S

Правило 1 амплитуда вероятности любого события (квантового перехода) всегда может быть представлена в виде скалярного произведения двух векторов, изображающих НАЧАЛЬНОЕ и КОНЕЧНОЕ состояния: АS→D = D | | S = D | S D | — бра-вектор, вектор конечного состояния (вектор-строка) | S — кет-вектор, вектор начального состояния (вектор-столбец) Координатное представление S 1 S 2 АS→D = D | S = ( D 1 D 2 … Dn ) • • Sn = ( Di S i ) i

Правило 2 любой вектор может быть представлен в виде линейной комбинации базисных векторов | S = S 1 | 1 + S 2 | 2 +. . . = Si | i D | = 1 | D 1 + 2 | D 2 +. . . = i | Di Физический смысл координат Si = i | S — амплитуда перехода частицы из начального состояния | S в конечное состояние i | (т. е. в iе базисное состояние прибора-анализатора) Di = D | i — амплитуда перехода частицы из начального состояния | i (т. е. i-го базисного состояния прибора-анализатора) в конечное состояние D |

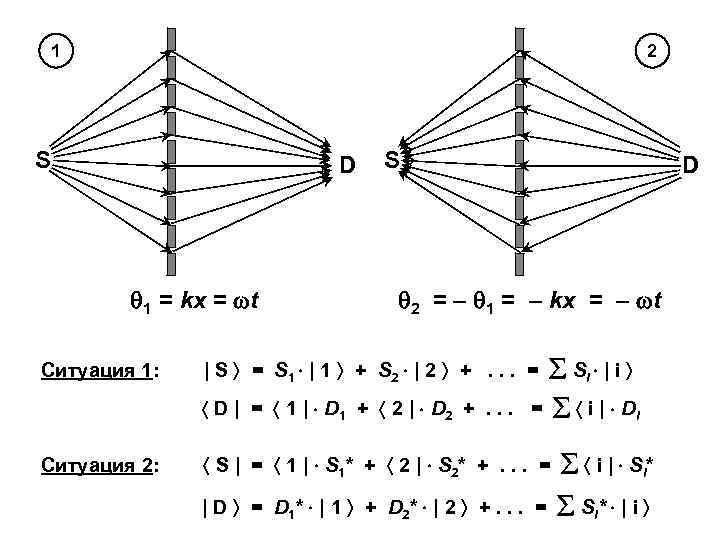
1 2 S D 1 = kx = t S D 2 = – 1 = – kx = – t Ситуация 2: | S = S 1 | 1 + S 2 | 2 +. . . = Si | i D | = 1 | D 1 + 2 | D 2 +. . . = Ситуация 1: i | Di S | = 1 | S 1 * + 2 | S 2 * +. . . = i | Si* | D = D 1 * | 1 + D 2 * | 2 +. . . = Si* | i

Вывод: каждое состояние можно представить двумя экземплярами вектора, которые являются ЭРМИТОВО СОПРЯЖЕННЫМИ относительно друга |S = S|+ D | = | D + «бра» -векторы D | используются для представления к о н е ч н ы х состояний, «кет» -векторы | S используются для представления н а ч а л ь н ы х состояний

Анализ векторов состояния Проблема: для вычисления амплитуд необходимы координатные представления векторов состояния АS→D = ( D 1 D 2 … Dn ) • S 1 S 2 • = ( Di S i ) Sn | S = S 1 | 1 + S 2 | 2 +. . . = Si | i D | = 1 | D 1 + 2 | D 2 +. . . = i | Di { | 1 | 2 . . . | n } = ? ? ? Спектральный анализатор А = А 1 | 1 • А=? • • • А = Аn | n Базисный набор

Правило 3 любое базисное состояние является собственным для некоторого спектрального анализатора ( А ), т. е. для этого состояния одна из наблюдаемых (А) имеет точно определенное значение, выраженное одним числом: А = Аi. Анализ вектора состояния S 1 | 1 |S =? • А • • Sn | n Si = i | Si |2 = P (A = Ai) | S i |2 = P i = 1 Условие нормировки | S = S 1 | 1 + S 2 | 2 +. . . + Sn | n

Представления векторов состояния Прибор А: | А = а 1 | А 1 + а 2 | А 2 +. . . = аi | Аi , где аi = Аi | Прибор B: | В = b 1 | B 1 + b 2 | B 2 +. . . = bi | Bi , где bi = Bi | Прибор C: | С = c 1 | C 1 + c 2 | C 2 +. . . = ci | Ci , где ci = Ci | Один и тот же вектор может быть представлен в разных координатных системах (в разном базисе)

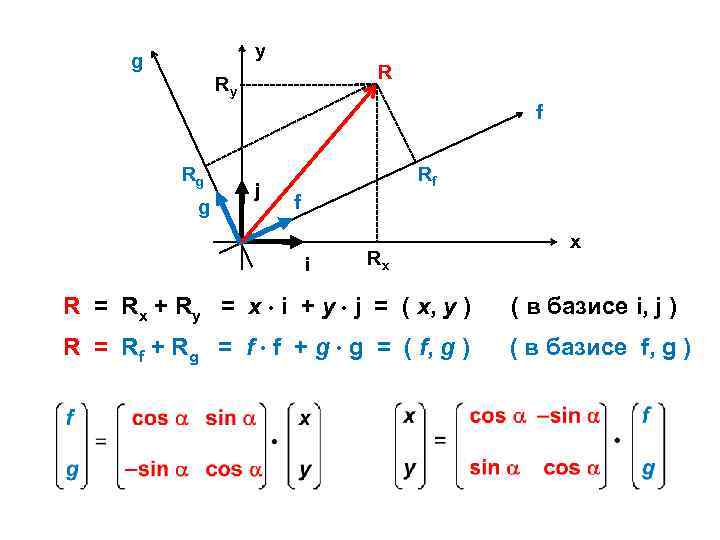
y g R Ry f Rg g j Rf f i Rx x R = Rx + Ry = x i + y j = ( x, y ) ( в базисе i, j ) R = Rf + Rg = f f + g g = ( f, g ) ( в базисе f, g )

| А UB A UA B | В UB A и UA B — матричные операторы преобразования координат вектора от одного базиса к другому UB A = (UA B)+ (UB A)+ = UA B Унитарные операторы А и В — з а в и с и м ы е наблюдаемые

Независимые наблюдаемые Прибор А: | А = а 1 | А 1 + а 2 | А 2 +. . . + аn | Аn = (a 1, a 2, …, аn) Прибор B: | В = b 1 | B 1 + b 2 | B 2 +. . . + bn | Bn = (b 1, b 2, …, bm) Прибор C: | С = c 1 | C 1 + c 2 | C 2 +. . . + cn | Cn = (c 1, c 2, …, ck) «Прямая» сумма векторов | ABC = | А | В | С | ABC = (a 1, a 2, …, аn, b 1, b 2, …, bm, c 1, c 2, …, ck)

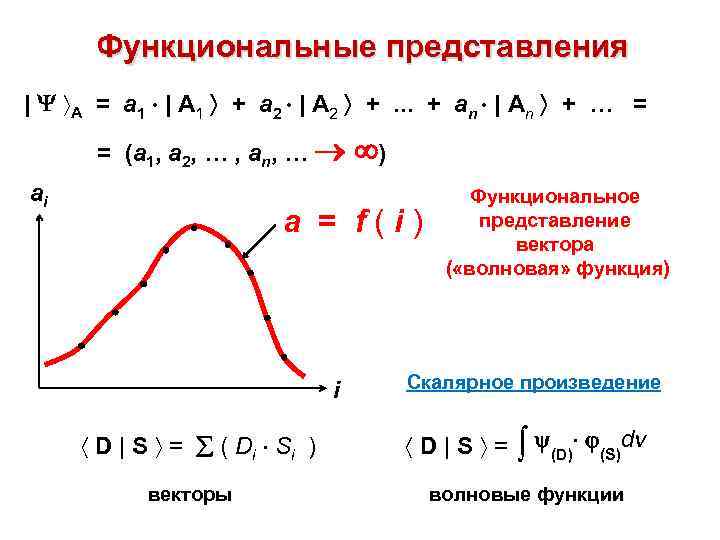
Функциональные представления | А = а 1 | А 1 + а 2 | А 2 +. . . + аn | Аn + … = = (a 1, a 2, … , an, … ai ) a = f(i) i D | S = ( Di S i ) векторы Функциональное представление вектора ( «волновая» функция) Скалярное произведение D|S = (D) (S)dv волновые функции

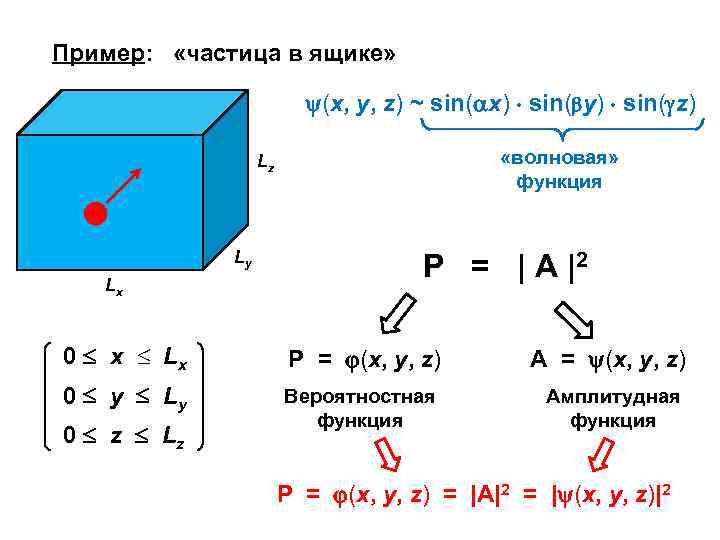
Пример: «частица в ящике» (x, y, z) ~ sin( x) sin( y) sin( z) «волновая» функция Lz Ly Lx P = | A |2 0 x Lx P = (x, y, z) A = (x, y, z) 0 y Ly Вероятностная функция Амплитудная функция 0 z Lz P = (x, y, z) = |A|2 = | (x, y, z)|2

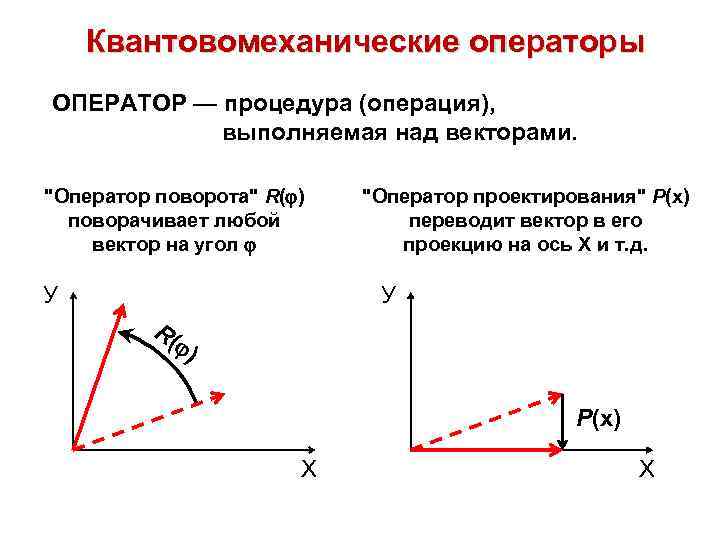
Квантовомеханические операторы ОПЕРАТОР — процедура (операция), выполняемая над векторами. "Оператор поворота" R( ) поворачивает любой вектор на угол У "Оператор проектирования" Р(х) переводит вектор в его проекцию на ось Х и т. д. У R( ) Р(х) Х Х

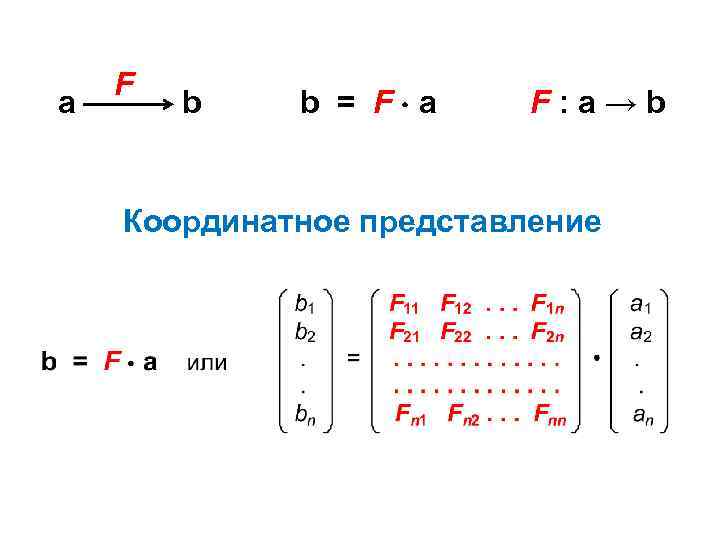
a F b b = F a F: a→b Координатное представление

Функциональное представление Оператор дифференцирования d [ (х) ] = '(х) dx функция производная Оператор интегрирования F(x) = первообразная [ (х)] dx функция

Явный вид оператора зависит от использованного базиса b=F • a 1 -й базис ( b )1 = ( F )1 • ( a )1 U 12 2 -й базис U 21 U 12 U 21 ( b )2 = ( F )2 • ( a )2

Связь между представлениями оператора F ( F )1 = U 12 • ( F )2 • U 21 ( F )2 = U 21 • ( F )1 • U 12 = (U 21)– 1 = (U 21)+ U 21 = (U 12)– 1 = (U 12)+ Унитарные операторы

Спектральные свойства операторов Каждый оператор F имеет: набор СОБСТВЕННЫХ ВЕКТОРОВ (функций) ( f 1, f 2, . . . , fn ) набор СОБСТВЕННЫХ ЗНАЧЕНИЙ (чисел) ( f 1, f 2, . . . , fn ) которые удовлетворяют «уравнению на собственные значения» : F • f = f • f

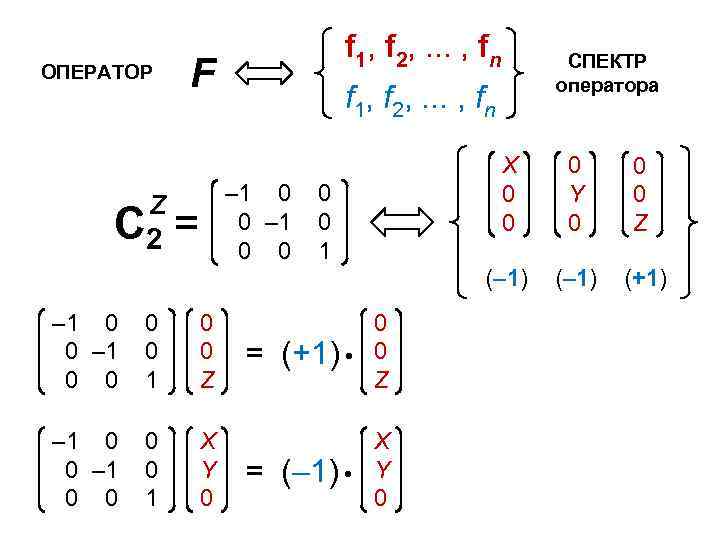
ОПЕРАТОР f 1, f 2, . . . , fn F f 1, f 2, . . . , fn – 1 0 0 z С 2 = – 1 0 0 0 0 1 0 0 Z – 1 0 0 0 0 1 X Y 0 СПЕКТР оператора 0 0 1 = 0 (+1) • 0 Z = X (– 1) • Y 0 X 0 0 0 Y 0 0 0 Z (– 1) (+1)

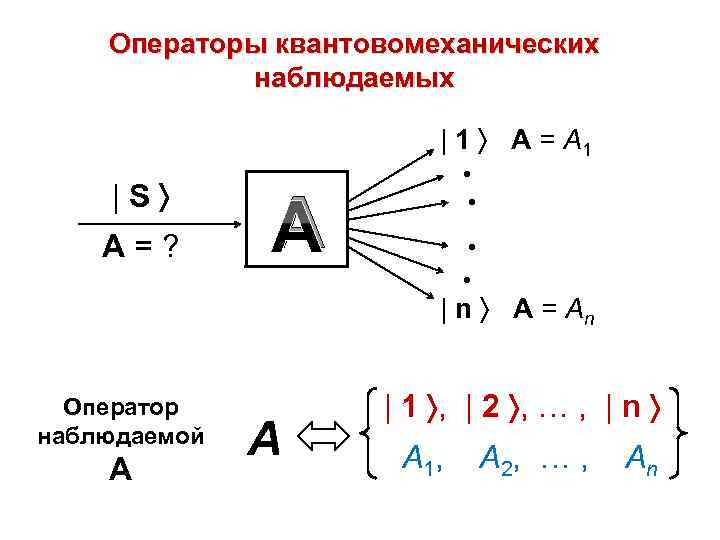
Операторы квантовомеханических наблюдаемых | 1 A = A 1 |S A=? • • А • • | n A = An Оператор наблюдаемой А A | 1 , | 2 , … , | n A 1, A 2, … , An

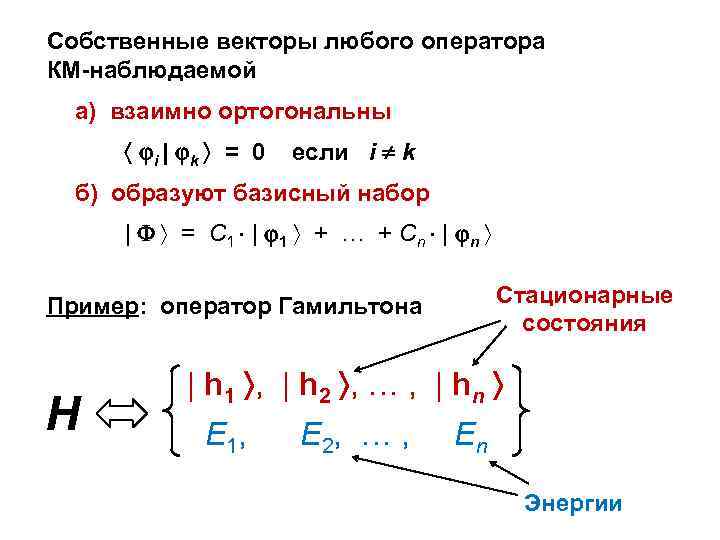
Собственные векторы любого оператора КМ-наблюдаемой а) взаимно ортогональны i | k = 0 если i k б) образуют базисный набор | = С 1 | 1 + … + С n | n Стационарные состояния Пример: оператор Гамильтона Н | h 1 , | h 2 , … , | hn E 1, E 2, … , En Энергии

Квантовые переходы в атоме 2 s | 1 s = A 1 s→ 2 s = 0 (векторы 1 s и 2 s взаимно ортогональны, так как принадлежат спектру одного и того же оператора Н) Представление нестационарных состояний | = С 1 | h 1 + С 2 | h 2 + … + Сn | hn | = (С 1, С 2, … , Сn) | Вода = 2 | Н + 1 | О = (2, 0, 0, 0, 1, 0, … )

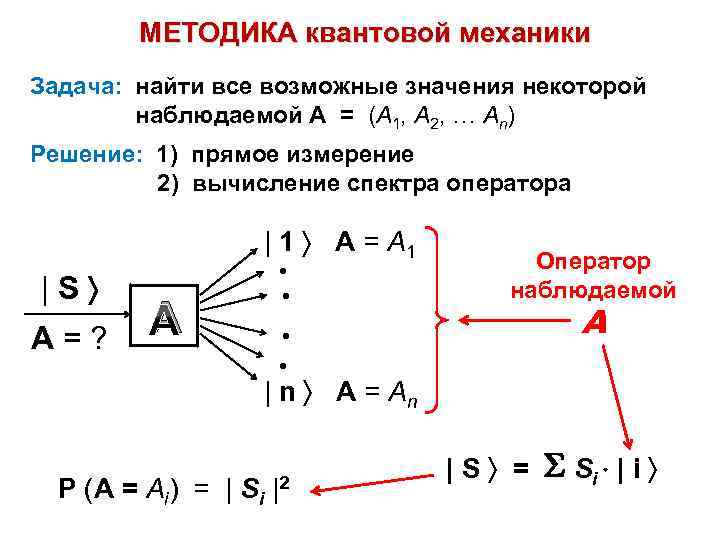
МЕТОДИКА квантовой механики Задача: найти все возможные значения некоторой наблюдаемой А = (А 1, А 2, … Аn) Решение: 1) прямое измерение 2) вычисление спектра оператора | 1 A = A 1 |S A=? • • А Оператор наблюдаемой А • • | n A = An P (A = Ai) = | Si |2 |S = Si | i

Выводы 1. Всякой механической наблюдаемой А можно сопоставить оператор А 2. Оператор А является математической моделью спектрального анализатора: • собственные значения оператора А являются допустимыми значениями наблюдаемой А, которые обнаруживаются в ходе реального измерения • собственные векторы (функции) оператора А описывают собственные состояния (выходные пучки) спектрального анализатора и могут быть использованы для анализа векторов состояний

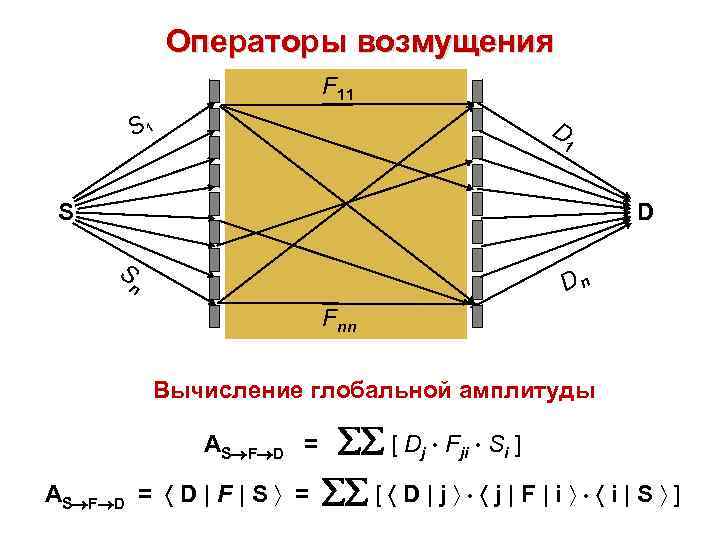
Операторы возмущения F 11 D S 1 1 S Dn n Fnn Вычисление глобальной амплитуды АS F D = D | F | S = [ Dj Fji Si ] [ D | j j | F | i i | S ]

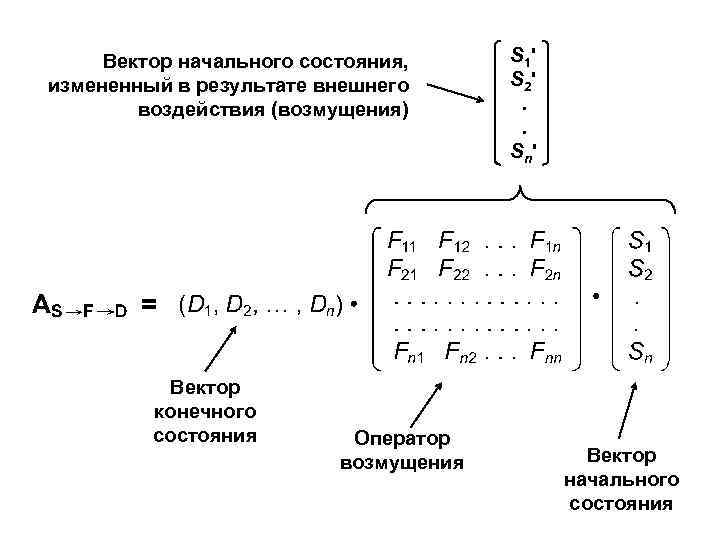
Вектор начального состояния, измененный в результате внешнего воздействия (возмущения) Вектор конечного состояния Оператор возмущения S 1 ' S 2 '. . Sn ' Вектор начального состояния

Вывод В квантовой механике используют три разновидности операторов 1. Операторы наблюдаемых Применение а) вычисление допустимых значений наблюдаемых (собственные значения), б) использование собственных вектров в качестве базисных наборов для анализа векторов состояния

2. Операторы возмущения Применение Описание влияния внешних тел или полей (электромагнитных, гравитационных и др. ) на движение частиц 3. Унитарные операторы Применение Преобразование координатных представлений векторов и операторов от одного базиса к другому