Математический анализ Непрерывность числовых функций Содержание n

Математический анализ Непрерывность числовых функций

Содержание n Непрерывность числовых функций n Свойства функций, непрерывных в точке n Приращение независимой переменной и приращение функции n Свойства функций, непрерывных на отрезке

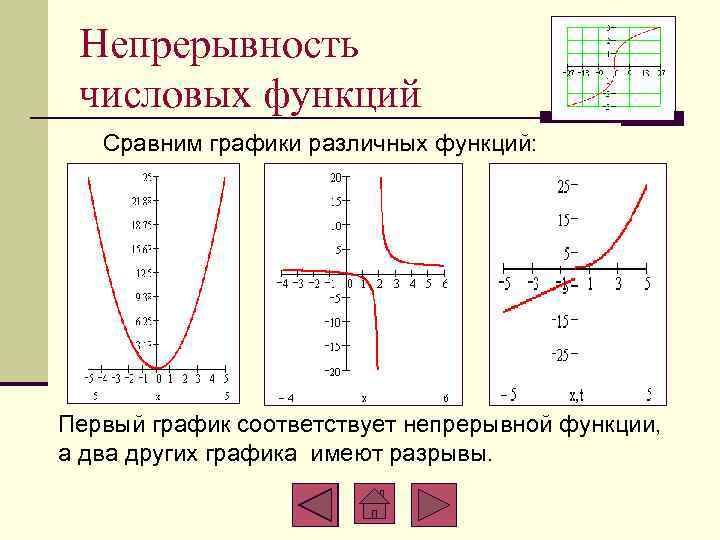Непрерывность числовых функций Сравним графики различных функций: Первый график соответствует непрерывной функции, а два других графика имеют разрывы.

Непрерывность числовых функций Функция f(x) называется непрерывной в точке xo, если она удовлетворяет условиям: 1. f(x) определена в точке xo; 2. имеет конечный предел при x xo; 3. . n

Непрерывность числовых функций n Следствие. Из определения следует, что т. е. для непрерывной функции возможна перестановка символов предела и функции. n Например,

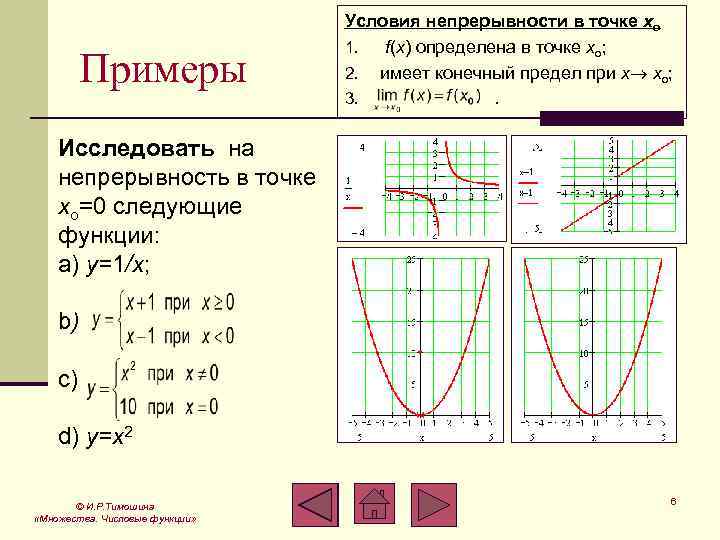Примеры Условия непрерывности в точке xo 1. f(x) определена в точке xo; 2. имеет конечный предел при x xo; 3. . Исследовать на непрерывность в точке xо=0 следующие функции: a) y=1/x; b) c) d) y=x 2 © И. Р. Тимошина «Множества. Числовые функции» 6

Решение в точке xo=0 функция не является непрерывной, т. к. в этой точке она не определена; b) в точке xo=0 функция не является непрерывной, (пределы функции слева и справа разные; c) в точке xo=0 функция не является непрерывной, т. к. ; d) в точке xo=0 функция является непрерывной. a) © И. Р. Тимошина «Множества. Числовые функции» Условия непрерывности в точке xo 1. f(x) определена в точке xo; 2. имеет конечный предел при x xo; 3. . a) b) c) d) 7

Свойства функций, непрерывных в точке 1. Если функции непрерывны в точке xo, то f(x)+g(x), f(x)∙g(x) и f(x)/g(x) (при условии, что g(x)≠ 0) являются функциями, непрерывными в точке xo. 2. Если функция f(x) непрерывна в точке xo и f(xo)>0 , то существует такая окрестность точки xo, в которой f(x)>0. 3. Если функция f(u) непрерывна в точке uo, а функция g(x) непрерывна в точке xo, причём g(xo)= uo, то сложная функция f(g(x)) непрерывна в точке xo.

Виды точек разрыва n Точки неустранимого разрыва первого рода (существуют односторонние конечные пределы функции слева и справа, не равные другу). n Точки устранимого разрыва первого рода (существуют односторонние конечные пределы функции слева и справа, равные другу). n Точки разрыва второго рода (хотя бы один из односторонних пределов равен бесконечности или не существует).

Вопрос на засыпку Какие из данных функций являются непрерывными в точке xо=1? В случае нарушения непрерывности, установить характер точки разрыва: © И. Р. Тимошина «Множества. Числовые функции» 10

Решение в точке xо=1 разрыв 2 рода. Функция непрерывна в точке xо=1 устранимый разрыв 1 рода. в точке xо=1 неустранимый разрыв 1 рода. © И. Р. Тимошина «Множества. Числовые функции» 11

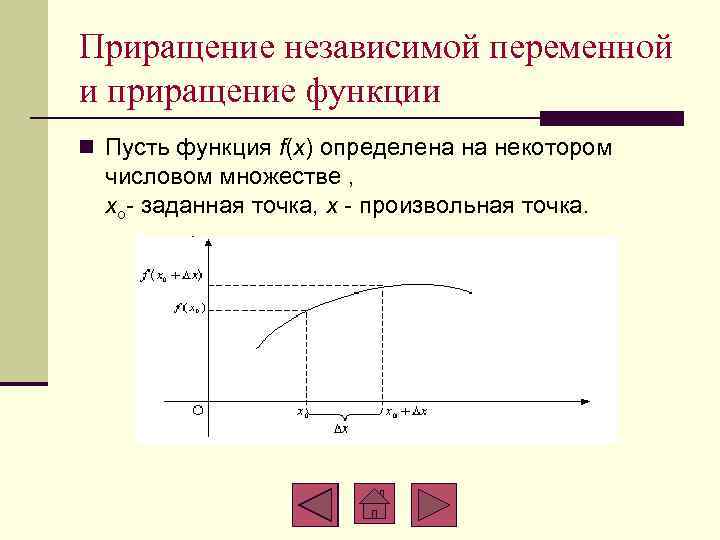Приращение независимой переменной и приращение функции n Пусть функция f(x) определена на некотором числовом множестве , xo- заданная точка, x - произвольная точка.

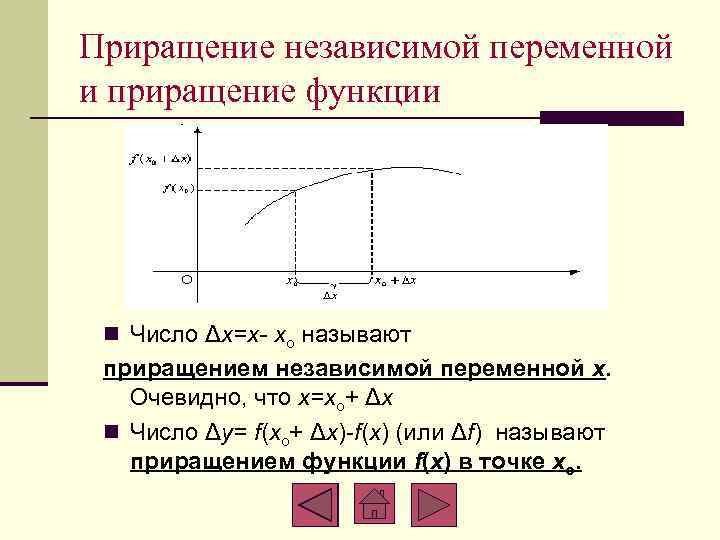Приращение независимой переменной и приращение функции n Число Δx=x- xo называют приращением независимой переменной x. Очевидно, что x=xo+ Δx n Число Δy= f(xo+ Δx)-f(x) (или Δf) называют приращением функции f(x) в точке xo.

Замечание Условия непрерывности в точке xo 1. f(x) определена в точке xo; 2. имеет конечный предел при x xo; 3. . n Отметим, что непрерывность функции f(x) в точке xo равносильна условию . Другими словами, малому изменения аргумента соответствует малое изменение значения функции. n Это условие может также служить определением непрерывности функции f(x) в точке xo. © И. Р. Тимошина «Множества. Числовые функции» 14

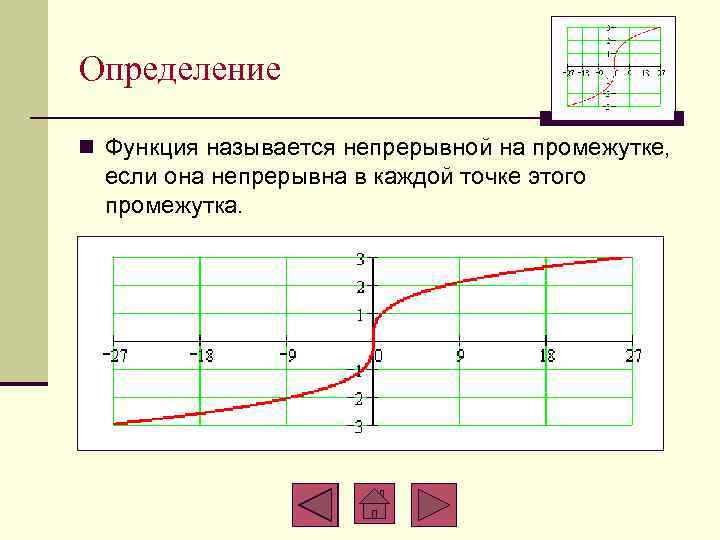Определение n Функция называется непрерывной на промежутке, если она непрерывна в каждой точке этого промежутка.

Теоремы о функциях, непрерывных на отрезке n Пусть функция f(x) непрерывна на отрезке [a, b]. Теорема 1 (первая теорема Вейерштрасса). Функция f(x) ограничена на отрезке [a, b]. Теорема 2 (вторая теорема Вейерштрасса). Функция f(x) достигает на отрезке [a, b] своего наименьшего и наибольшего значения. n Теорема 3 (теорема Больцано-Коши). Пусть m и M соответственно наименьшее и наибольшее значения функции f(x) на отрезке [a, b]. Тогда отрезок [m, M] является областью значений функции f(x).

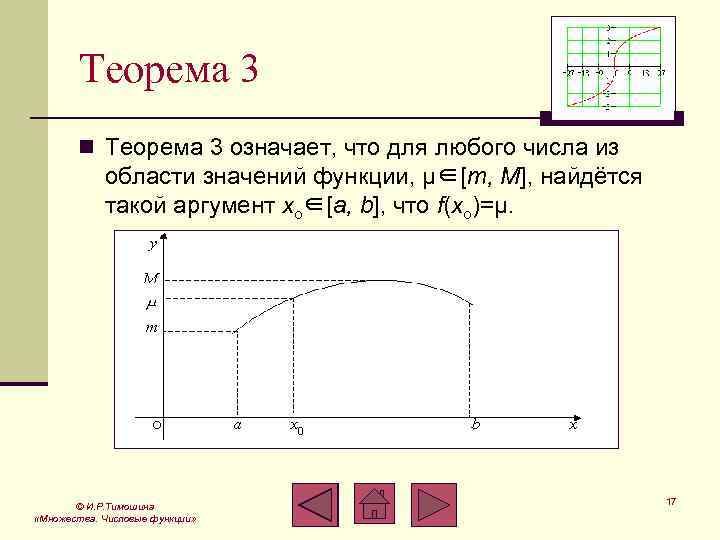Теорема 3 n Теорема 3 означает, что для любого числа из области значений функции, μ∈[m, M], найдётся такой аргумент xo∈[a, b], что f(xo)=μ. © И. Р. Тимошина «Множества. Числовые функции» 17

Пример n Записать вид приращений числовых функций в точке xo и вычислить эти приращения при xo=1 и ∆x=1: a) y=2 x 2; b) y=x 2+1 © И. Р. Тимошина «Множества. Числовые функции» n Решение. a) f(xo) =2 xo 2; f(xo+∆x)= 2(xo+∆x) 2; ∆f (xo)=f(xo+∆x) f(xo)= =2(xo+∆x) 2 2 xo+2=2∆x; ∆f (xo) =2∆x; ∆f (1) =2∙ 1=2. n Заметим, что приращение линейной функции не зависит от xo и пропорционально ∆x. 18

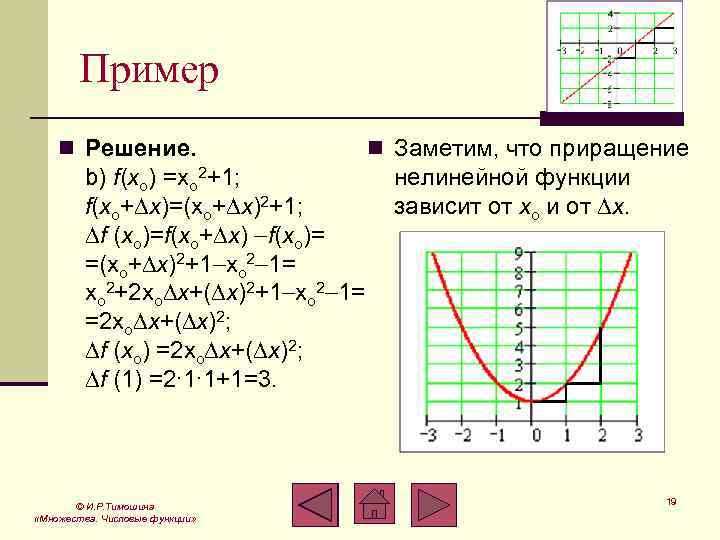Пример n Решение. b) f(xo) =xo 2+1; f(xo+∆x)=(xo+∆x)2+1; ∆f (xo)=f(xo+∆x) f(xo)= =(xo+∆x)2+1 xo 2 1= xo 2+2 xo∆x+(∆x)2+1 xo 2 1= =2 xo∆x+(∆x)2; ∆f (xo) =2 xo∆x+(∆x)2; ∆f (1) =2∙ 1∙ 1+1=3. © И. Р. Тимошина «Множества. Числовые функции» n Заметим, что приращение нелинейной функции зависит от xo и от ∆x. 19

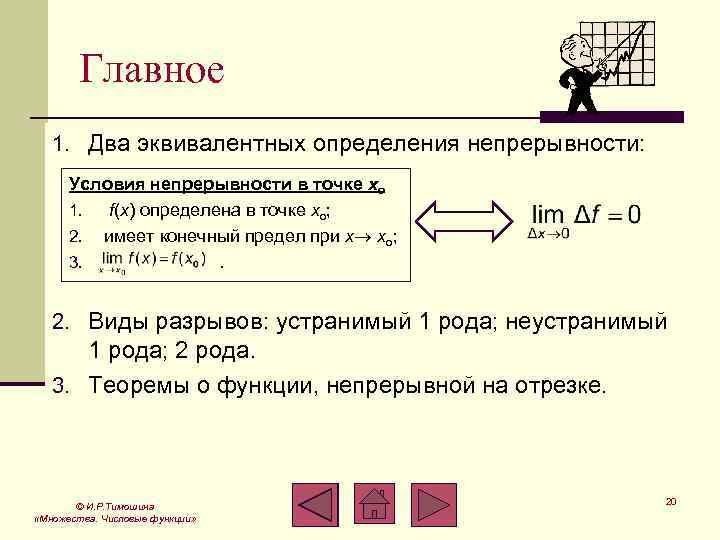Главное 1. Два эквивалентных определения непрерывности: Условия непрерывности в точке xo 1. f(x) определена в точке xo; 2. имеет конечный предел при x xo; 3. . 2. Виды разрывов: устранимый 1 рода; неустранимый 1 рода; 2 рода. 3. Теоремы о функции, непрерывной на отрезке. © И. Р. Тимошина «Множества. Числовые функции» 20