МАн_1 Последоват.pptx
- Количество слайдов: 64

Математический анализ не менее всеобъемлющ, чем сама природа. Ж. Фурье Математический анализ Множества. Числовые последовательности

Логическая символика , … ! : некоторые высказывания или утверждения, относительно каждого из которых можно сказать – истинно оно или ложно «не » , т. е. отрицание утверждения «из утверждения следует утверждение » ; (символ импликации) «утверждение эквивалентно утверждению » ; « и равносильны» «утверждение является необходимым и достаточным условием » (символ эквивалентности) «каково бы ни было» , «любой» , «каждый» (квантор всеобщности); a A - для любого элемента a, принадлежащего множеству «существует» (квантор существования); a A – существует элемент a принадлежащий множеству А «единственный» (символ единственности) «такое, что» , «выполняется» , «удовлетворяет условию»

1 Понятие множества Множество (set) – некоторая, вполне определенная совокупность объектов произвольной природы, каждый их которых называется элементом множества. Георг Кантор (1845 -1918) Множество есть «объединение в одно целое объектов, хорошо различимых нашей интуицией или мыслью» .

Примеры множеств

Элементы множества (set members) Объекты, которые образуют множество, называются его элементами. Бесконечное множество содержит бесконечное число элементов. Конечное множество состоит из конечного числа элементов. Пример. Множество натуральных чисел – бесконечное множество. Множество студентов факультета – конечное множество.

Обозначения В дальнейшем множества будем обозначать прописными латинскими буквами, элементы – строчными латинскими. a ∈ A – «элемент a принадлежит множеству A» . a A – «элемент a не принадлежит множеству A»

Пустое множество (empty set, null set) Множество, не содержащее ни одного элемента, называется пустым и обозначается . Пример. Множество оценок первокурсника в первом семестре. в зачетке

Подмножество (subset) Множество B называется подмножеством множества A, если каждый элемент множества В является элементом множества А. Рис. Диаграмма Эйлера-Венна, изображающая подмножество В множества А Пример. Множество первокурсников есть подмножество множества студентов.

Равные множества (equal sets) Два множества А и В называются равными, если они состоят из одних и тех же элементов. Обозначение: A=B Например, A = {филателисты} и B={аквалангисты} А=В если любой филателист является одновременно аквалангистом и наоборот.

Универсальное множество (universal set) Универсальное множество U есть совокупность всех рассматриваемых в задаче множеств. Пример. Имеются два множества: A = { 3, 7, 11, 15 } B = { 2, 4, 6, …, 2 n, … } Множество U = { все целые числа } является универсальным множеством для множеств A и B.

Числовые множества • N ={1, 2, 3…} – множество натуральных чисел; • Z ={0, 1, 2, 3, … } – множество целых чисел ; • Q – множество рациональных чисел вида • I – множество иррациональных чисел, т. е. чисел, представимых в виде бесконечной десятичной непериодической дроби, например , e, , …; • R – множество действительных (вещественных) чисел, образуемое совокупностью рациональных Q и иррациональных I чисел:

2 Операции над множествами 2 -1 Объединение (сумма) 2 -2 Пересечение (произведение) 2 -3 Разность (вычитание) 2 -4 Симметрическая разность 2 -5 Дополнение 2 -6 Свойства операций

2 -1 Объединение множеств (sum of sets) • Объединением (суммой) двух множеств А и В называется множество С, состоящее из всех элементов, принадлежащих хотя бы одному из данных множеств: Обозначение: А + В = А В Пример. A = { жители Москвы } и B = { жители Подмосковья } С = А В = { жители Москвы или Подмосковья } ВОПРОС: D = { 1, 3, 5} и F = { 2, 4, 6}. Тогда M = D F = ?

2 -2 Пересечение множеств (intersections of sets) • Пересечением (произведением) двух множеств А и В называется множество D, состоящее из всех элементов, одновременно принадлежащих каждому из данных множеств: Обозначение: А·В = А В Пример. A = { студенты, участвовавшие в концерте } B = { студенты ЗАДАЧА 104 группы } D = { студенты 104 группы, участвовавшие в концерте } A = (0; 5) и B = [4; 9) D = А В?

2 -3 Разность множеств (set difference) • Разностью двух множеств А и В называется множество F, состоящее из всех элементов принадлежащих множеству А, но не принадлежащих множеству В: Обозначение: А – В = А В Пример. ЗАДАЧА A = [1; 3] и B = N A=Rи. B=I F = А – В = (1; 2) (2; 3) F=АI=?

2 -4 Симметрическая разность множеств • Симметрической разностью двух множеств А и В называется множество G, состоящее из всех элементов исходных множеств, не принадлежащие одновременно обоим исходным множествам: Обозначение: А ∆ В Пример А={1, 2, 3, 4, 5} B={3, 4, 5, 6, 7} G=А ∆ В ={1, 2, 6, 7}

2 -5 Дополнение к множеству (set compliment) Дополнением к множеству A называется множество элементов универсального множества, не принадлежащих A: Ᾱ=U–A Обозначение: Пример. A = { девушки 11 группы } U = { все студенты 11 группы } Ᾱ = { юноши 11 группы }

2 -6 Свойства операций над множествами Для введенных операций присущи следующие свойства:

3 Числовые промежутки и ограниченные множества

Числовые промежутки

Окрестность точки (neighborhood of point) Абсолютная величина разности двух чисел |x – a| означает расстояние между двумя точками х и а числовой прямой как для случая х<а, так и для х>а. Окрестность точки c – произвольный интервал (a, b), содержащий точку с.
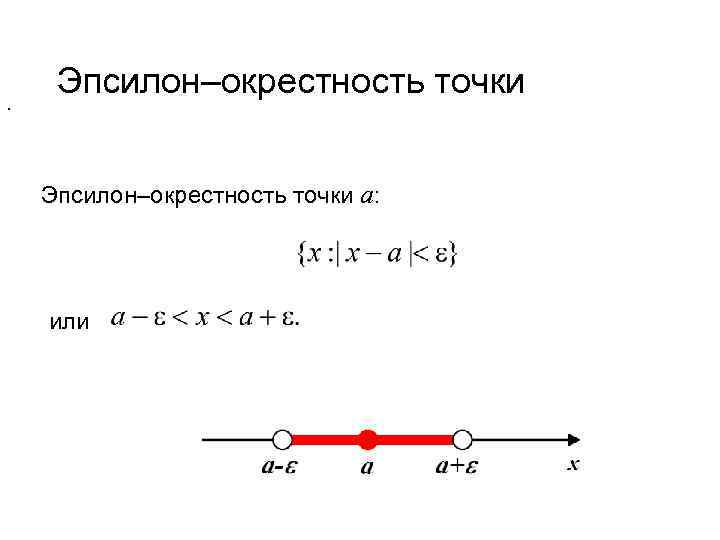
. Эпсилон–окрестность точки a: или

Ограниченные множества

Грани числовых множеств Если множество Х ограничено сверху, то говорят, что множество имеет верхнюю границу Наименьшая из верхних границ множества Х называется точной верхней гранью и обозначается sup. X. Наибольшая из нижних границ множества Х называется точной нижней гранью и обозначается inf. X.

Задача. Найти точную верхнюю и точную нижнюю грани множества [0, 1). Решение. 1. Это множество не имеет наибольшего элемента, так как для найдется такой, что Множество верхних граней для данного полуинтервала [0, 1) – это множество с наименьшим элементом, равным 1. Отсюда причем 1 не принадлежит заданному множеству.

С другой стороны, наименьший элемент для рассматриваемого множества существует и равен 0. Множество нижних граней – это множество с наибольшим элементом, равным 0, который и является точной нижней гранью полуинтервала Таким образом, причем Неограниченные множества: (-∞, ∞), (-∞, 2], [-5, ∞). ТВГ (-∞, 2] равна 2, ТНГ [-5, ∞) равна -5.

4 Числовые последовательности • 1 Определение последовательности • 2 Предел последовательности • 3 Теоремы о пределах • 4 Бесконечно большие и бесконечно малые последовательности • 5 Вычисление пределов

4 -1 Определение последовательности Если каждому натуральному числу n по определенному закону поставлено в соответствие некоторое число xn, то множество пронумерованных чисел x 1, x 2, x 3, … называется числовой последовательностью. Элементы этого множества называются членами числовой последовательности.

Примеры последовательностей
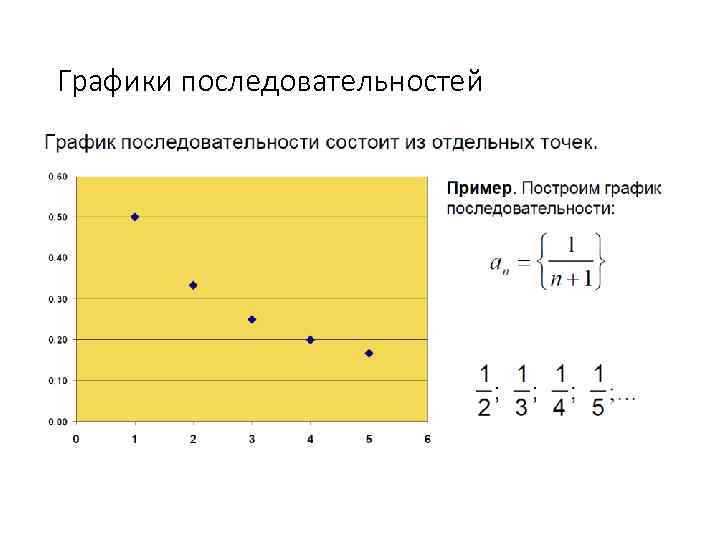
Графики последовательностей
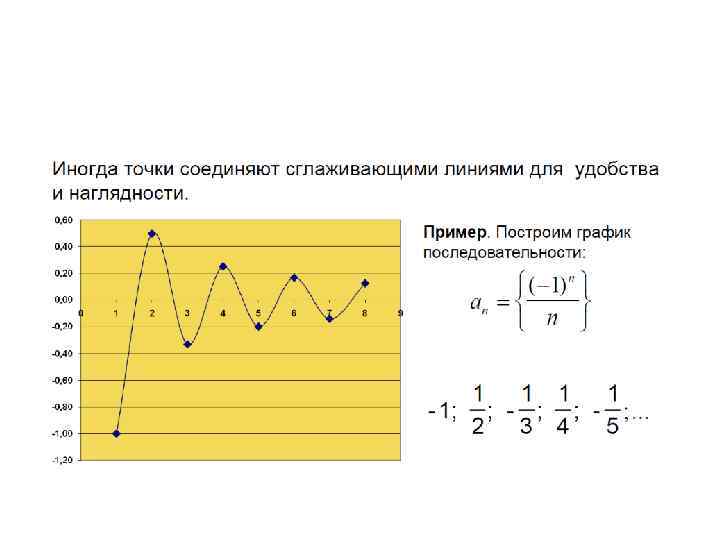

Ограниченная последовательность

ПРИМЕРЫ
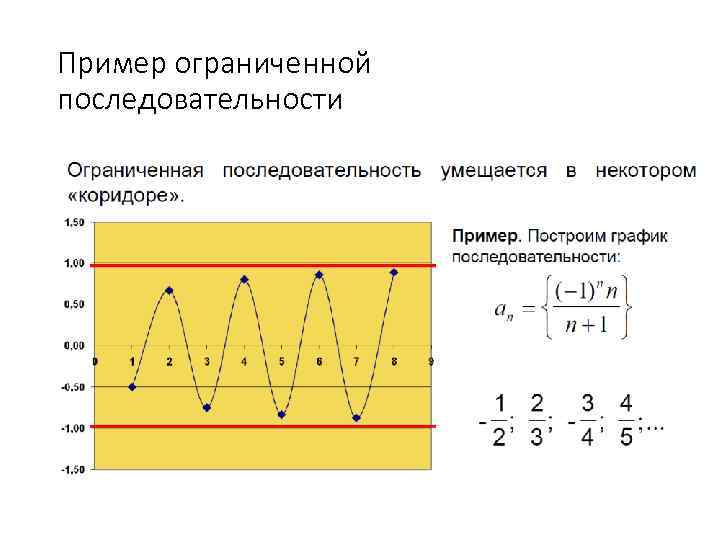
Пример ограниченной последовательности


4 -2 Предел последовательности • Понятие последовательности • Определение предела последовательности • Геометрический смысл

Предел последовательности

Предел числовой последовательности

Определение предела в кванторах

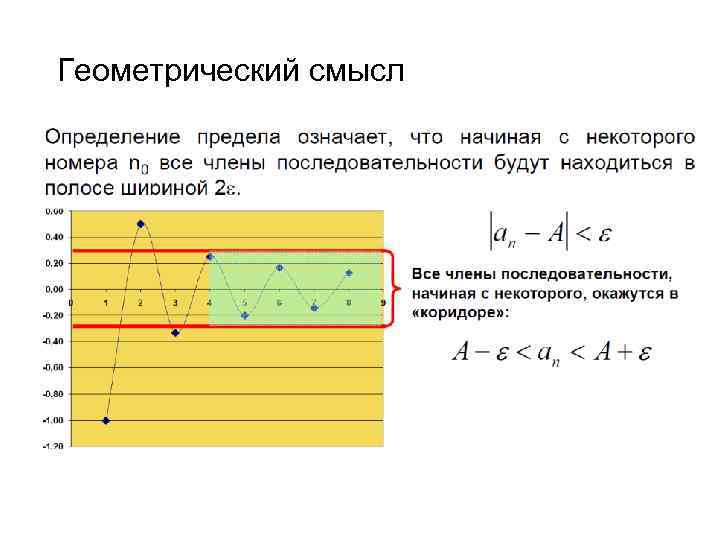
Геометрический смысл

пример 1

решение примера 1

решение примера 1(продолжение)

пример 2



пример 3

Кому нужен такой «формализм» ?

Ответ

4 -3 Основные теоремы о пределах • Единственность предела • Предел суммы, произведения, частного • Признаки существования предела

Единственность предела

Предел суммы

Пределы произведения и частного
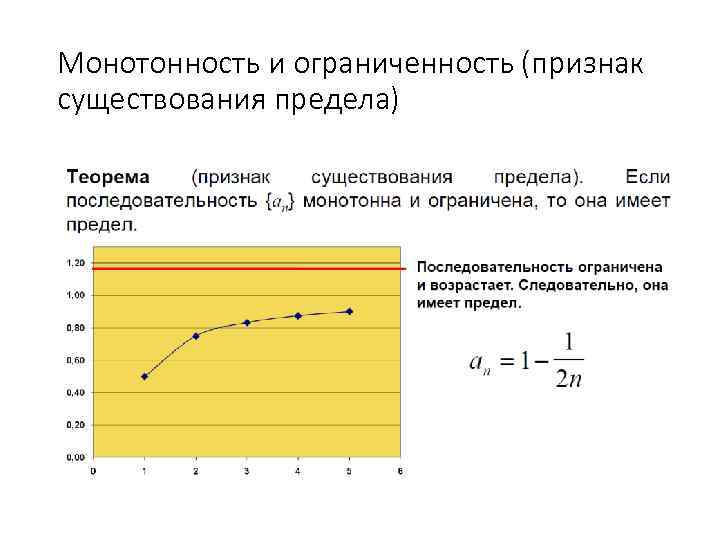
Монотонность и ограниченность (признак существования предела)
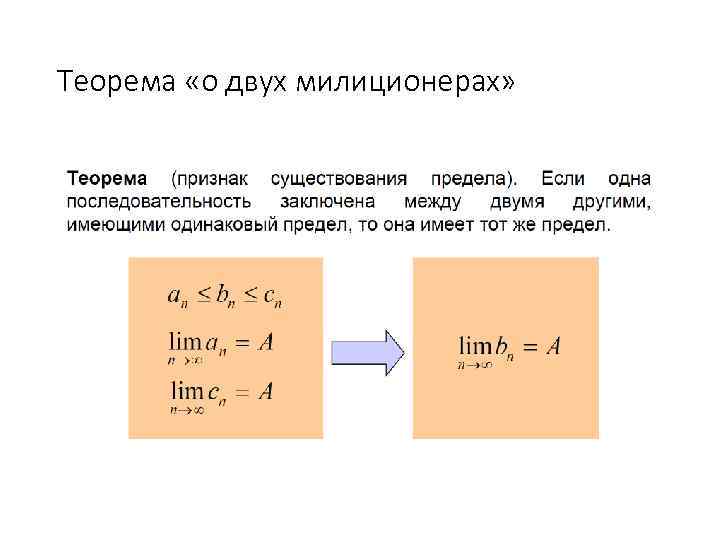
Теорема «о двух милиционерах»

4 -4 Бесконечно большие и бесконечно малые последовательности



Свойства бесконечно малых последовательностей


Примеры бесконечно малых последовательностей

4 -5 Вычисление пределов
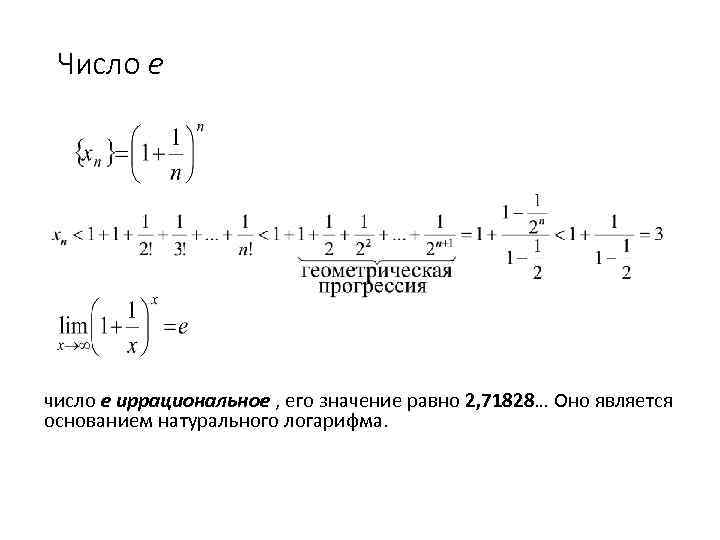
Число е число е иррациональное , его значение равно 2, 71828… Оно является основанием натурального логарифма.
МАн_1 Последоват.pptx