Математический анализ Методы интегрирования рациональных дробей и рациональных тригонометрических функций
Содержание n Рациональные дроби и их свойства n Метод неопределённых коэффициентов разложения правильных рациональных дробей на простейшие n Интегрирование рациональных дробей n Интегрирование рациональных тригонометрических функций И. Р. Тимошина "Математический анализ" 2
Рациональные a xn+a xn-1+…+a n n-1 0 _________ дроби R(x)= b xm+b xm-1+…+b m m-1 0 n Рациональной дробью называется выражение вида an≠ 0; bm≠ 0; m и n – целые числа, ai и bi – вещественные числа. n Выражение Qn(x)=anxn+an-1 xn-1+…+ a 0 называется многочленом степени n. К примеру, 5 x 3+4 x 2 3, многочлен третьей степени. И. Р. Тимошина "Математический анализ" 3
Рациональные a xn+a xn-1+…+a n n-1 0 _________ дроби R(x)= b xm+b xm-1+…+b m m-1 0 n Дробь называется неправильной, если старшая степень числителя n больше или равна старшей степени знаменателя m. n Дробь называется правильной, если старшая степень числителя n меньше старшей степени знаменателя m. И. Р. Тимошина "Математический анализ" 4
Рациональные a xn+a xn-1+…+a n n-1 0 _________ дроби R(x)= b xm+b xm-1+…+b m m-1 n Например, дроби 0 - неправильные. n Дробь И. Р. Тимошина "Математический анализ" - правильная. 5
Рациональные a xn+a xn-1+…+a n n-1 0 _________ дроби R(x)= b xm+b xm-1+…+b m m-1 0 n Теорема. Любую неправильную дробь можно представить в виде двух слагаемых: многочлена (целой части) и правильной рациональной дроби. n Примеры. И. Р. Тимошина "Математический анализ" 6
Простейшие рациональные дроби n Простейшими называются дроби вида: n Замечание. Должно выполняться условие: дискриминант p 2 4 ac<0. n Теорема. Каждую правильную рациональную дробь можно представить единственным способом в виде суммы простейших дробей. И. Р. Тимошина "Математический анализ" 7
Пример Разложить правильную дробь на простейшие. Решение. 1. x 3+2 x 2 8 x=x(x 2+2 x 8)=x(x+4)(x 2) 2. Представим данную дробь в виде суммы простейших дробей с неопределёнными коэффициентами: Так как дроби равны и знаменатели этих дробей равны, то равны и числители этих дробей. И. Р. Тимошина "Математический анализ" 8
Пример 3. При x=0 получим: 2= 8 А ⇒ А= 1/4. При x= 4 получим: 26=24 В ⇒ В=13/12 При x=2 получим: 2=12 С ⇒ С=1/6 Ответ. И. Р. Тимошина "Математический анализ" 9
Интегралы от простейших дробей И. Р. Тимошина "Математический анализ" 10
Интегралы от простейших дробей Обозначим Выделим полный квадрат: Преобразуем числитель: И. Р. Тимошина "Математический анализ" 11
И. Р. Тимошина "Математический анализ" 12
Вопрос на засыпку Пример. Найти интегралы: Решение. И. Р. Тимошина "Математический анализ" 13
Интегрирование рациональных тригонометрических функций n Пусть R(t) – некоторая рациональная дробь. Если вместо переменной t в дроби стоит любая тригонометрическая функция, то выражение называют рациональной тригонометрической функцией. n К примеру, алгебраическая дробь: тригонометрическая рациональная функция: И. Р. Тимошина "Математический анализ" 14
Интегрирование рациональных тригонометрических функций n Идея интегрирования таких функций заключается в такой замене переменных, при которых тригонометрическая рациональная функция превратится в алгебраическую рациональную дробь. n Рассмотрим некоторые подстановки, позволяющие интегрирование рациональных тригонометрических функций свести к интегрированию рациональных дробей. И. Р. Тимошина "Математический анализ" 15
Интегрирование рациональных тригонометрических функций 1. Если у тригонометрической дроби R(t) t=sinx, а подынтегральное выражение имеет вид: R(sinx)∙cosxdx, то замена t=sinx приведёт к интегрированию алгебраической дроби. Пример. 2. Если подынтегральное выражение имеет вид: R(cosx)∙sinxdx, то необходима замена t=cosx. И. Р. Тимошина "Математический анализ" 16
Интегрирование рациональных тригонометрических функций 3. Если подынтегральное выражение имеет вид: R(tgx)dx, то необходима замена t=tgx. В этом случае x=arctgt; dx=dt/(1+ t 2). 4. В общем случае подстановка всегда позволит преобразовать тригонометрическую дробь в алгебраическую, т. к. : x=2 arctgt И. Р. Тимошина "Математический анализ" 17
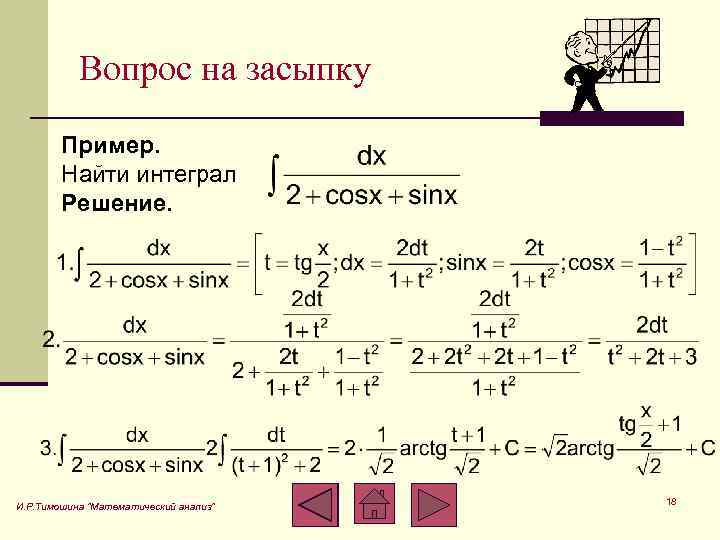
Вопрос на засыпку Пример. Найти интеграл Решение. И. Р. Тимошина "Математический анализ" 18
Скачать презентацию Математический анализ Методы интегрирования рациональных дробей и рациональных
През Методы интегрирования.ppt