Математический анализ 1 семестр 6 1 Определение

Математический анализ, 1 семестр 6. 1. Определение производной.

6. 1. Определение производной. Теорема 6. 1. Для существования f (x 0) н. и д. существования обеих односторонних производных f (x 0+0), f (x 0 - 0) и их равенство. Определение 6. 2. Функция f, определенная в окрестности точки x 0 называется дифференцируемой в точке x 0, если существует число А, такое, что приращение функции представимо в виде f = f(x) - f(x 0) = A(x - x 0)+o (x – x 0), x x 0 Теорема 6. 2. Для существования f (x 0) необходимо и достаточно, чтобы f была дифференцируема в точке x 0. Математический анализ, 1 семестр

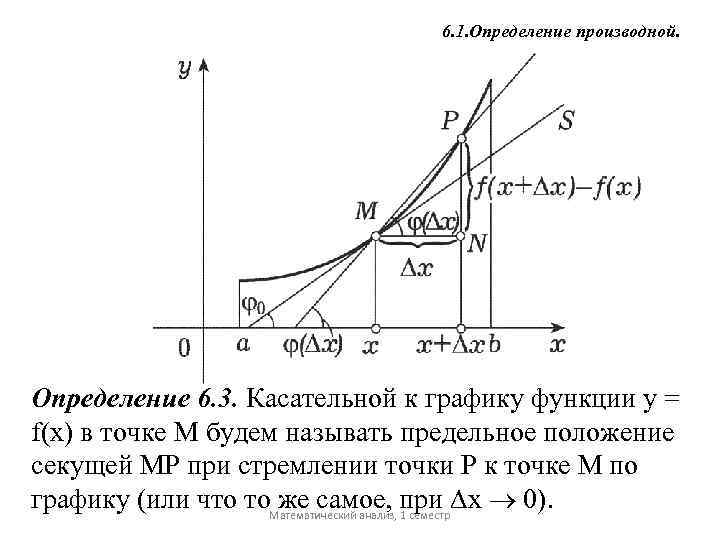6. 1. Определение производной. Определение 6. 3. Касательной к графику функции у = f(x) в точке М будем называть предельное положение секущей МР при стремлении точки Р к точке М по графику (или что то. Математический анализ, 1 семестр х 0). же самое, при

6. 2. Дифференциал функции Уравнение касательной к графику функции в точке x 0 : y - y 0= f (x 0)(x - x 0). Теорема 6. 3 ( Необходимое условие дифференцируемости ) Если функция дифференцируема в точке, то она непрерывна в этой точке. 6. 2. Дифференциал функции Определение 6. 4. Главная линейная часть приращения функции A x в определении дифференцируемости функции f=f(x) - f(x 0)=A(x - x 0)+o (x – x 0), x x 0 называется дифференциалом функции f(x) в точке x 0 и обозначается df(x 0)=f (x 0) x= A x. Математический анализ, 1 семестр

6. 3. Основные правила дифференцирования f=const, f =0, df=0 x=0 f=u+v, f =u +v , df = du+dv f=uv, f =u v+v u, df = u dv + v du Следствие. (cf(x)) =cf (x), (c 1 f 1(x)+…+cnfn(x)) = c 1 f 1(x)+…+ cn f n(x) f=u/v, v(x 0) 0 и производная существует, то f =(u v-v u)/v 2. Математический анализ, 1 семестр

6. 3. Основные правила дифференцирования Математический анализ, 1 семестр

, 6. 4. Производные элементарных функций Математический анализ, 1 семестр

6. 4. Производные элементарных функций , 6. 5. Логарифмическое дифференцирование f (x)=f(x)(ln f(x)) Математический анализ, 1 семестр