Математические понятия предложения доказательства Составитель Титова Н Ф

Математические понятия, предложения, доказательства Составитель: Титова Н. Ф.

Математика n Наука о количественных отношениях и пространственных формах действительного мира

μαθημα n Познание, наука

ФЕДЕРАЛЬНЫЕ ГОСУДАРСТВЕННЫЕ ТРЕБОВАНИЯ К СТРУКТУРЕ ОСНОВНОЙ ОБЩЕОБРАЗОВАТЕЛЬНОЙ ПРОГРАММЫ ДОШКОЛЬНОГО ОБРАЗОВАНИЯ (ФГТ) Программа определяет содержание и организацию образовательного процесса для детей дошкольного возраста и направлена на формирование общей культуры, развитие физических, интеллектуальных и личностных качеств, ……

ФЕДЕРАЛЬНЫЕ ГОСУДАРСТВЕННЫЕ ТРЕБОВАНИЯ К СТРУКТУРЕ ОСНОВНОЙ ОБЩЕОБРАЗОВАТЕЛЬНОЙ ПРОГРАММЫ ДОШКОЛЬНОГО ОБРАЗОВАНИЯ (ФГТ) Содержание образовательной области "Познание" направлено на достижение целей развития у детей познавательных интересов, интеллектуального развития детей через решение следующих задач: n сенсорное развитие; n развитие познавательноисследовательской и продуктивной (конструктивной) деятельности; n формирование элементарных математических представлений; n формирование целостной картины мира, расширение кругозора детей

Мышление n это творческий, познавательный процесс, обобщенно и опосредованно отражающий отношения предметов и явлений, законы объективного мира

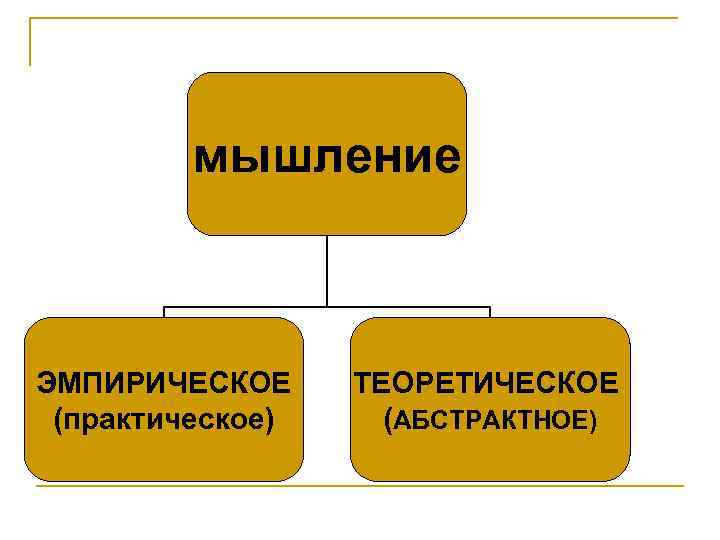мышление ЭМПИРИЧЕСКОЕ (практическое) ТЕОРЕТИЧЕСКОЕ (АБСТРАКТНОЕ)

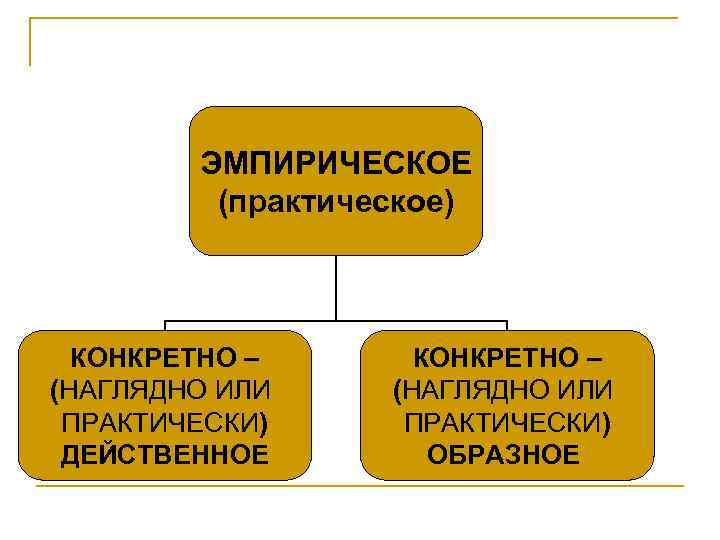ЭМПИРИЧЕСКОЕ (практическое) КОНКРЕТНО – (НАГЛЯДНО ИЛИ ПРАКТИЧЕСКИ) ДЕЙСТВЕННОЕ КОНКРЕТНО – (НАГЛЯДНО ИЛИ ПРАКТИЧЕСКИ) ОБРАЗНОЕ

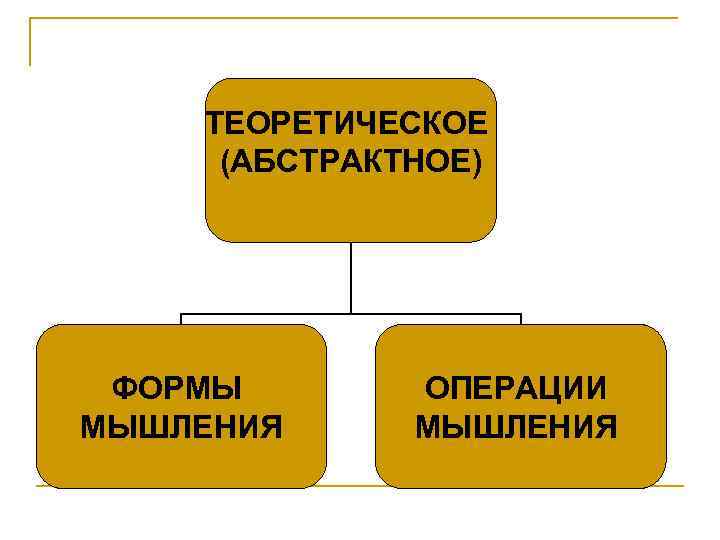ТЕОРЕТИЧЕСКОЕ (АБСТРАКТНОЕ) ФОРМЫ МЫШЛЕНИЯ ОПЕРАЦИИ МЫШЛЕНИЯ

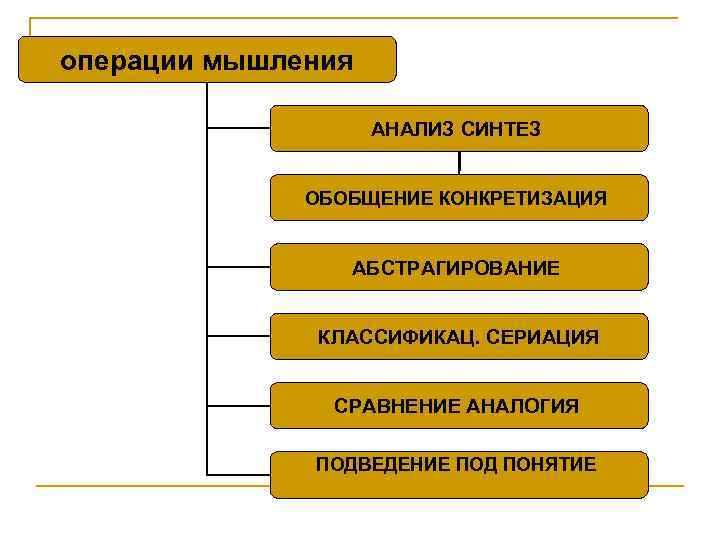операции мышления АНАЛИЗ СИНТЕЗ ОБОБЩЕНИЕ КОНКРЕТИЗАЦИЯ АБСТРАГИРОВАНИЕ КЛАССИФИКАЦ. СЕРИАЦИЯ СРАВНЕНИЕ АНАЛОГИЯ ПОДВЕДЕНИЕ ПОД ПОНЯТИЕ

ФОРМЫ МЫШЛЕНИЯ понятия суждения умозаключения

Логическим мышлением n называют мышление в форме понятий, суждений и умозаключений по правилам и законам мышления

Тема 1: 1. Математические понятия, предложения, доказательства

Логика (logos от латинского - слово, понятие, рассуждение, разум) n Наука о закономерностях и операциях правильного мышления

План 1. 2. 3. 4. 5. 6. Определение понятий. Объем и содержание понятия Явные и неявные определения. Структура определений понятий через род и видовое отличие. Требования к определению понятий Понятие высказывания. Конъюнкция, дизъюнкция, импликация высказываний Высказывательная форма (предикат ). Область определения и множество истинности предиката Правила построения отрицания высказываний Дедуктивные и индуктивные рассуждения. Простейшие схемы правильных рассуждений

1. ОПРЕДЕЛЕНИЕ ПОНЯТИЙ. ОБЪЕМ И СОДЕРЖАНИЕ ПОНЯТИЯ

Понятие n форма мышления, в которой фиксируются существенные признаки предмета (объекта) или класса однородных предметов(объектов )

Признаки n Существенные это признаки, отражающие коренную природу объектов n Несущественные это признаки, приобретение которых объектом не меняет его природу

Понятие n Содержанием понятия называется совокупность всех существенных признаков объекта n Объем понятия это совокупность всех объектов, обозначаемых одним и тем же термином

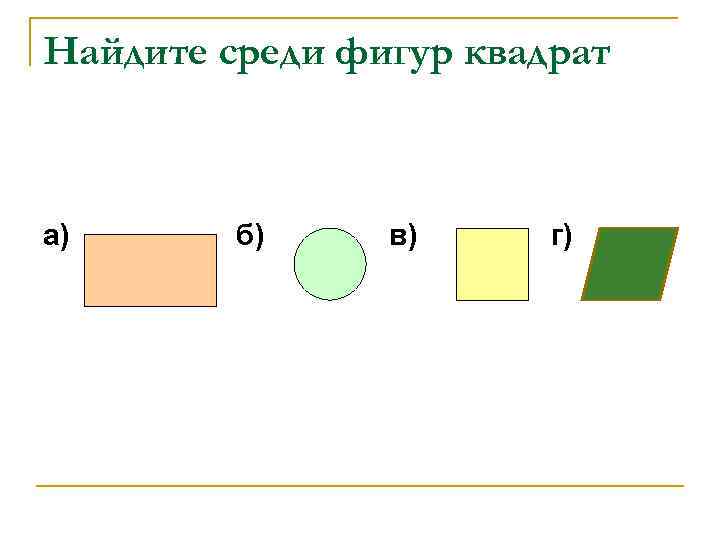Найдите среди фигур квадрат а) б) в) г)

2. Явные и неявные определения. Структура определений понятий через род и видовое отличие. Требования к определению понятий

Определение понятия n есть логическая операция, раскрывающая содержание понятия

Явное определение понятия Определяемое понятие = Определяющее понятие

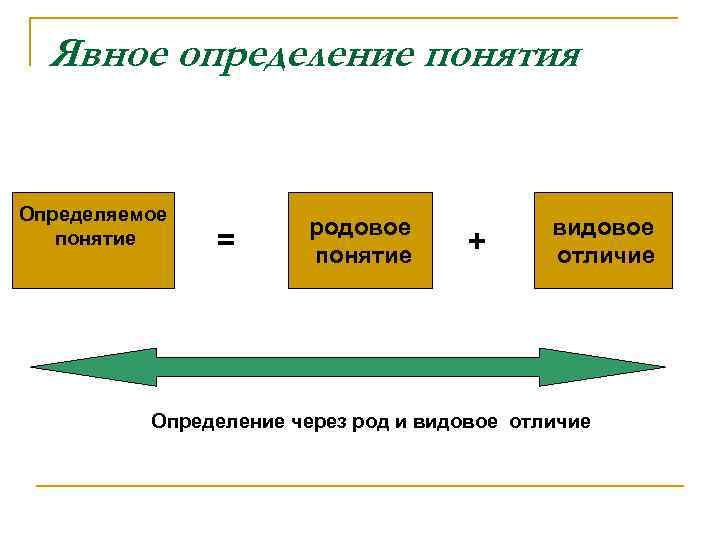Явное определение понятия Определяемое понятие = родовое понятие + видовое отличие Определение через род и видовое отличие

Определение понятия через род и видовое отличие (классическое) n Определение, в котором предметы определяемого понятия вводятся в объем более широкого понятия (родового) и с помощью отличительных признаков (видовых отличий)выделяются среди предметов этого более широкого понятия

Неявные определения понятия n Остенсивные (от лат. ostentus – показывание) – определения, в которых значение слов вводят непосредственно путем показа, демонстрации предметов, которые эти слова обозначают n Семантические (от гр. semantikas – обозначающий) определения, в которых определенному обозначению непосредственно ставятся в соответствие предметы объема данного понятия

Задачи на распознавание (на подведение под понятие) 1. 2. 3. 4. 5. Выделить понятие, под которое нужно подвести данный объект Установить, при каких условиях данный объект может относиться к данному понятию, т. е. необходимо дать определение понятия Выделить признаки, о которых идет речь в определении понятия Установить, обладает ли данный объект этими признаками Сделать вывод, можно ли данный объект подвести под понятие, назвать данным термином

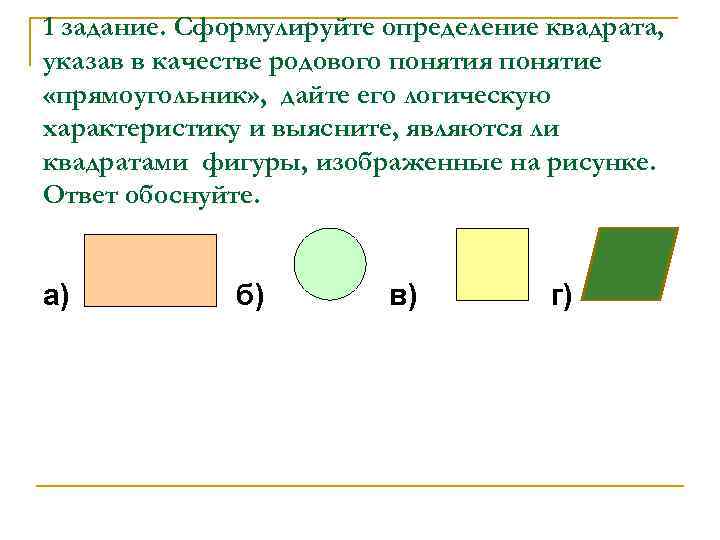1 задание. Сформулируйте определение квадрата, указав в качестве родового понятия понятие «прямоугольник» , дайте его логическую характеристику и выясните, являются ли квадратами фигуры, изображенные на рисунке. Ответ обоснуйте. а) б) в) г)

Требования к определению понятий 1. 2. 3. 4. 5. Определяемое и определяющее понятия должны быть соразмерены Правило запрета порочного круга Определение понятия не должно быть избыточным Определение понятия должно быть ясным Определение понятия не должно содержать отрицания

2 задание. Соразмерно ли определение понятия? 1. 2. Ромб это четырехугольник, у которого все углы прямые и стороны равны Треугольник называется равносторонним, если у него все стороны равны

3. Понятие высказывания. Конъюнкция, дизъюнкция, импликация, отрицание высказываний

Высказывание n Повествовательное предложение, о котором можно сказать истинно оно или ложно

ВЫСКАЗЫВАНИЕ ПРОСТОЕ СОСТАВНОЕ

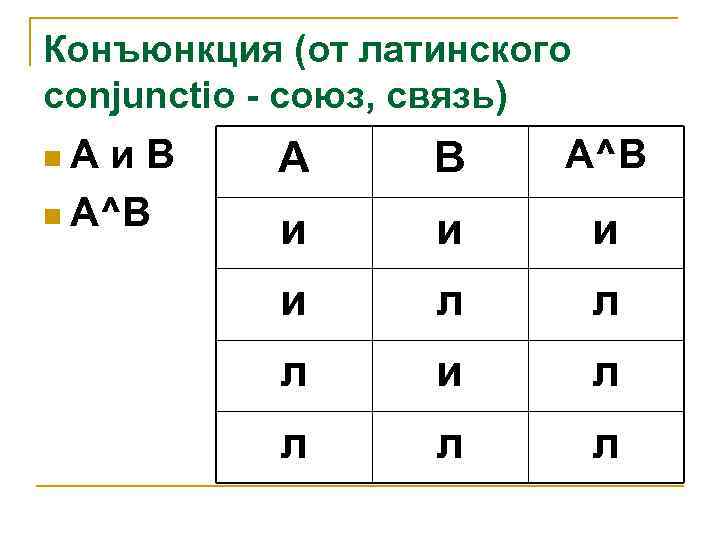Конъюнкция (от латинского сonjunctio - союз, связь) n. A и. B n A^B А В A^B и и л л л и л л

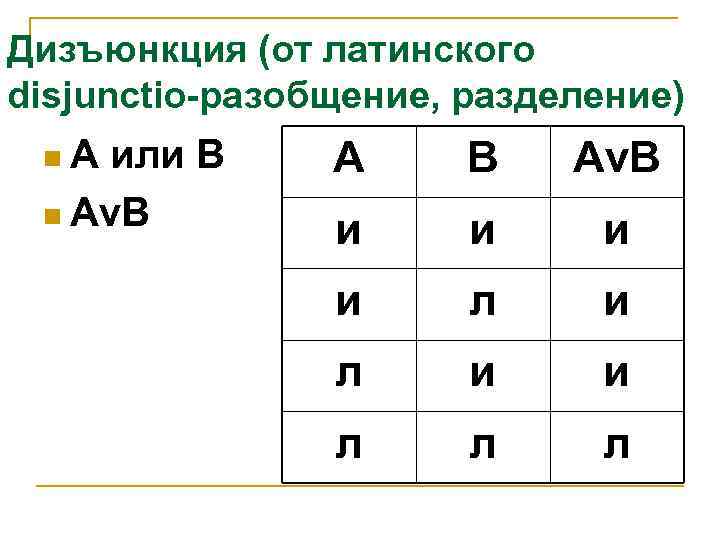Дизъюнкция (от латинского disjunctio-разобщение, разделение) n. A или B n Av. B А В Av. B и и л л л

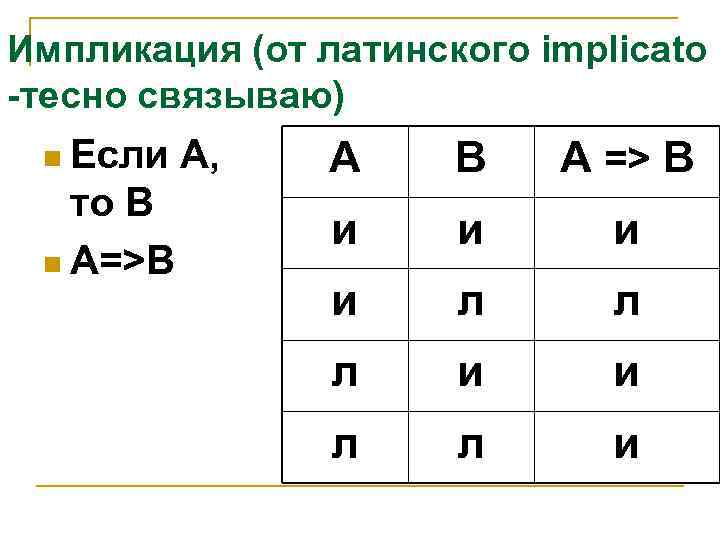Импликация (от латинского implicato -тесно связываю) n Если то B n A=>B A, А В A => B и и л л л и и л л и

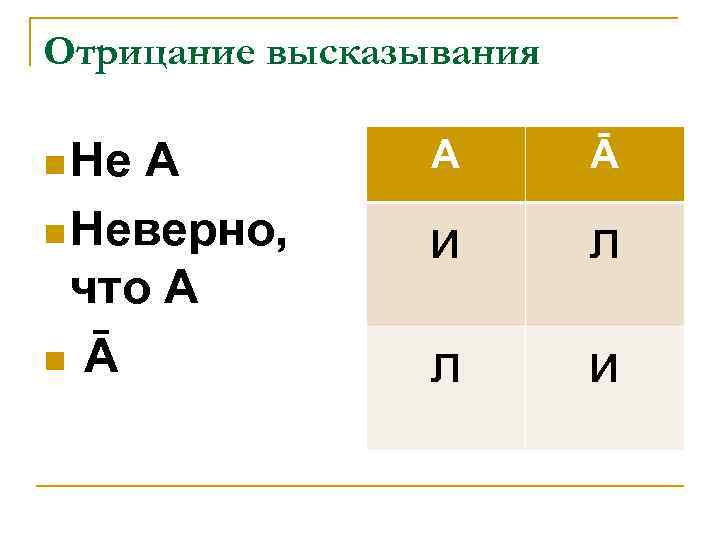Отрицание высказывания n Не А n Неверно, что А n Ā А Ā и л л и

Порядок определения значения истинности в составном высказывании ¯ 2. ^ 3. V 4. => 1.

3 задание. Определите значение истинности высказывания 1. AV D=>B^C, если A-и, D-л, B-и, C-л 2. A => (BV D)^C, если A-л, D-л, B-л, C-и

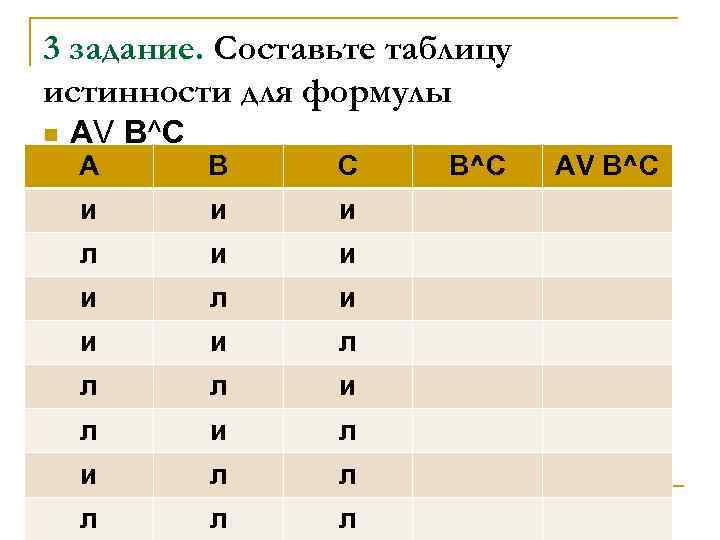3 задание. Составьте таблицу истинности для формулы n AV B^C A B C и и и л л л и л и л л л B^C AV B^C

4 задание. Будут ли равносильны высказывания? _____ n _ _ X V Y и X^Y

4. Высказывательная форма (предикат ). Область определения и множество истинности предиката

Высказывательная форма (предикат) n n Предложение с переменной или несколькими переменными, которое обращается в высказывание при подстановке вместо переменных их значений А(х), В(х, у)

Высказывательная форма (предикат) 1. Область определения Х 2. Множество истинности T

6 задание. Найдите область определения и множество истинности предиката 1. 2. А(х): Город х стоит на реке Исети В(х): 5 х +1=6

Квантор (от лат. quantum-сколько) n символ математической логики, логическая операция, дающая количественную характеристику области предметов, к которым относится выражение, получаемое в результате ее применения

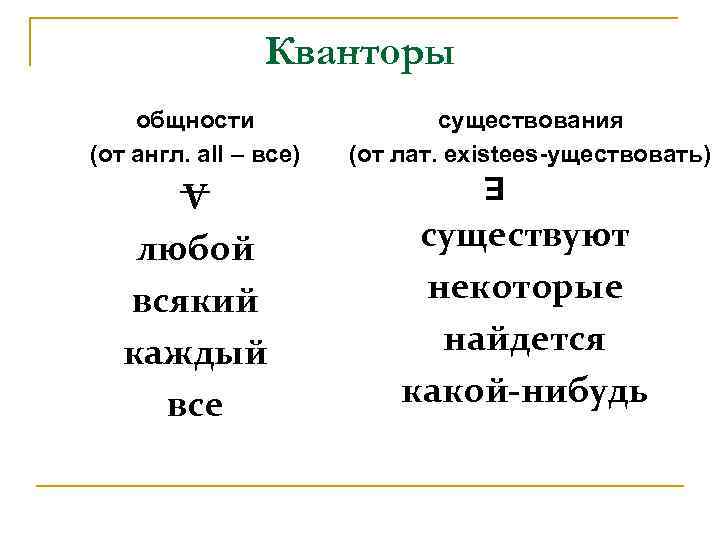Кванторы общности (от англ. all – все) существования (от лат. existees-уществовать) V любой всякий каждый все существуют некоторые найдется какой-нибудь Е

5. Правила построения отрицания высказываний

Способы построения отрицаний высказываний с кванторами 1. 2. Перед высказыванием – «неверно, что» Квантор общности (существования) заменить на квантор существования (общности), предложение, стоящее после квантора заменить на его отрицание

7 задание. Постройте отрицание высказывания. Определите значение истинности высказывания и его отрицания 1. 2. 3. 4. Любой прямоугольник является квадратом. Для любого действительного числа х справедливо неравенство х2>0 Существуют ромбы с разными сторонами Существуют действительные числа, которые не являются решением неравенства х+1<х

6. Дедуктивные и индуктивные рассуждения. Простейшие схемы правильных рассуждений

Рассуждения Дедуктивные Индуктивные

Правила вывода 1. Правило заключения (А=>В, А(а)) =>В(а) общая посылка частная посылка 2. Правило заключение отрицания (А=>В, В(а)) =>А(а) 3. Правило силлогизма (А=>В, В =>С) =>(А=>С)

8 задание. Определи истинность рассуждения 1. 2. 3. Если сумма цифр числа делится на 3, то число делится на 3. Сумма цифр числа 327 делится на 3, следовательно, число 327 делится на 3. Противоположные углы параллелограмма равны. Четырехугольник АВСD не является параллелограммом, следовательно, его противоположные углы не равны. Все отличники 3 класса спортсмены, все спортсмены 3 класса мальчики, следовательно, все отличники 3 класса мальчики

Спасибо за внимание! Желаю творческих успехов!