Математические понятия Лекция 2 Попова Е А

Математические понятия Лекция 2 Попова Е. А.

Понятия, которые изучаются в начальном курсе математики, обычно представляют в виде четырех групп: 1. 2. 3. 4. Понятия, связанные с числами и операциями над ними: число, цифра, сложение, слагаемое и др. Алгебраические понятия: выражение, равенство, уравнение и др. Геометрические понятия: прямая, отрезок, треугольник и т. д. Понятия, связанные с величинами и их измерением: длина, масса, единица величины и др.

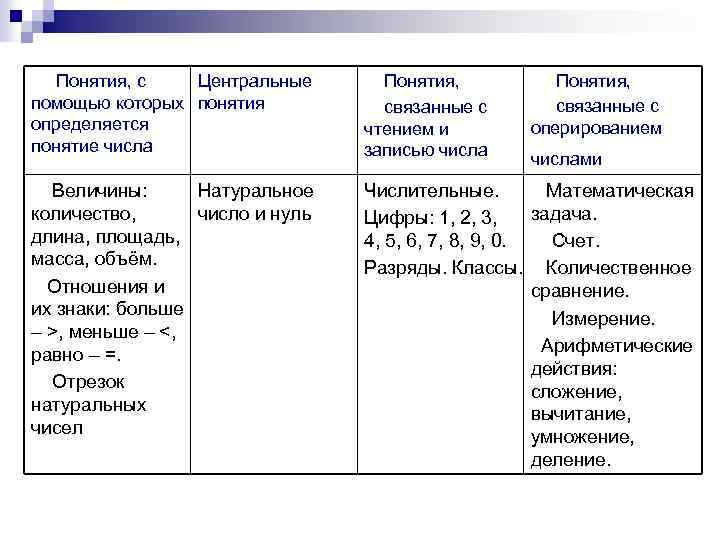Понятия, с Центральные помощью которых понятия определяется понятие числа Понятия, связанные с чтением и записью числа Понятия, связанные с оперированием Величины: Натуральное количество, число и нуль длина, площадь, масса, объём. Отношения и их знаки: больше – >, меньше – <, равно – =. Отрезок натуральных чисел Числительные. Математическая Цифры: 1, 2, 3, задача. 4, 5, 6, 7, 8, 9, 0. Счет. Разряды. Классы. Количественное сравнение. Измерение. Арифметические действия: сложение, вычитание, умножение, деление. числами

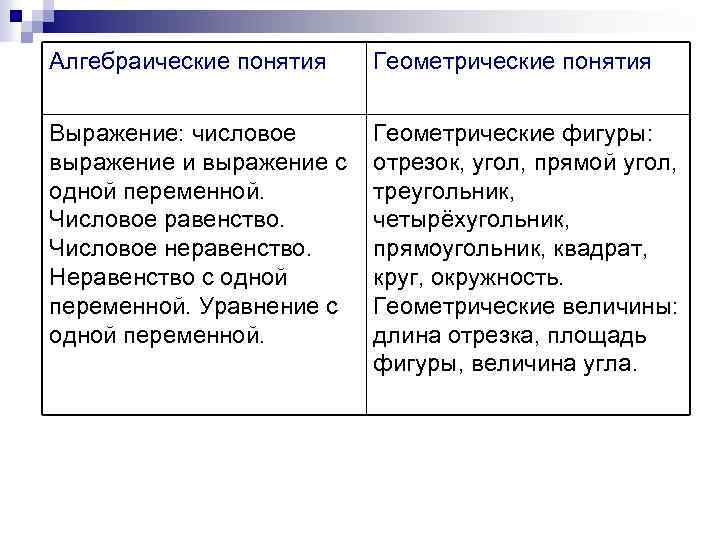Алгебраические понятия Геометрические понятия Выражение: числовое выражение и выражение с одной переменной. Числовое равенство. Числовое неравенство. Неравенство с одной переменной. Уравнение с одной переменной. Геометрические фигуры: отрезок, угол, прямой угол, треугольник, четырёхугольник, прямоугольник, квадрат, круг, окружность. Геометрические величины: длина отрезка, площадь фигуры, величина угла.

n n n Понятие рассматривают как форму мышления, отражающую объекты (предметы или явления) в их существенных и общих свойствах. Языковой формой понятия является слово или группа слов. Понятия не существуют в объективном мире. Они возникают в сознании человека и заменяют предметы и явления этого мира, являясь их идеальными образами. Иметь понятие об объекте – это значит уметь выделить его существенные признаки и отличить от всех других объектов.

Математические понятия, как и любые другие, существуют лишь в мышлении человека и в тех знаках и символах, которые образуют математический язык. n Всякий математический объект обладает определенными свойствами. Например, квадрат имеет четыре стороны, четыре прямых угла, равные диагонали. Можно указать и другие его свойства. n

Среди свойств объекта различают существенные и несущественные. Свойство считают существенным для объекта, если оно присуще этому объекту и без него он не может существовать. n Когда говорят о математическом понятии, то обычно имеют в виду множество объектов, обозначаемых одним термином (словом или группой слов). n

n n n Объем понятия – это множество всех объектов, которые обобщаются в понятии и обозначаются одним термином. Содержание понятия – это множество всех существенных свойств объекта, отраженных в этом понятии. Между объемом понятия и его содержанием существует взаимосвязь: если увеличивается объем понятия, то уменьшается его содержание, и наоборот. Например, понятие «прямоугольник» Объем данного понятия – это множество различных прямоугольников, а в его содержание входят такие свойства прямоугольников, как «иметь четыре прямых угла» , «иметь равные противоположные стороны» , «иметь равные диагонали» и т. д.

n Любое понятие нельзя усвоить, не осознав его взаимосвязи с другими понятиями. Поэтому важно знать, в каких отношениях могут находиться понятия, и уметь устанавливать эти связи. n Отношения между понятиями тесно связаны с отношениями между их объемами, т. е. множествами. Например, если a – «прямоугольник» , b – «четырехугольник» , то их объемы A и B находятся в отношении включения (A B и A B), поскольку всякий прямоугольник является четырехугольником. Поэтому можно утверждать, что понятие «прямоугольник» – видовое по отношению к понятию «четырехугольник» , а понятие «четырехугольник» – родовое по отношению к понятию «прямоугольник» . Если A = B, то говорят, что понятия a и b тождественны. n

n n Во-первых, понятия рода и вида относительны: одно и то же понятие может быть родовым по отношению к одному понятию и видовым по отношению к другому. Например, понятие «прямоугольник» – родовое по отношению к понятию «квадрат» и видовое по отношению к понятию «четырехугольник» . Во-вторых, для данного понятия часто можно указать несколько родовых понятий. Так, для понятия «прямоугольник» родовыми являются понятия «четырехугольник» , «параллелограмм» , «многоугольник» . Среди них можно указать ближайшее. Для понятия «прямоугольник» ближайшим является понятие «параллелограмм» . В-третьих, видовое понятие обладает всеми свойствами родового понятия. Например, квадрат, являясь видовым понятием по отношению к понятию «прямоугольник» , обладает всеми свойствами, присущими прямоугольнику. Так как объем понятия – множество, удобно, устанавливая отношения между объемами понятий, изображать их при помощи кругов Эйлера.

В процессе мышления с понятиями выполняют операции n n n Обобщение понятия – это логическая операция, которая состоит в переходе от понятия с меньшим объемом (большим содержанием) к понятию с большим объемом (но меньшим содержанием). Обобщение понятия – это переход от видового понятия к родовому. При этом происходит расширение объема за счет отбрасывания существенных признаков. Например, обобщая понятие «прямоугольник» можно перейти к понятию «четырехугольник» , отбросив такое свойство, как «иметь все углы прямые» . Ограничение понятия – это логическая операция, которая состоит в переходе от понятия с большим объемом к понятию с меньшим объемом. Ограничение понятия – это переход от родового понятия к видовому. При этом сужение объема происходит за счет расширения содержания. Например, понятие «четырехугольник» можно ограничить, добавив к его содержанию свойство «иметь все прямые углы» . В результате получим понятие «прямоугольник» . Определение понятия – это логическая операция, с помощью которой раскрывается содержание понятия. По способу выявления содержания понятия различают явные и неявные определения. Среди явных определений в математике чаще всего используются определения через род и видовое отличие.

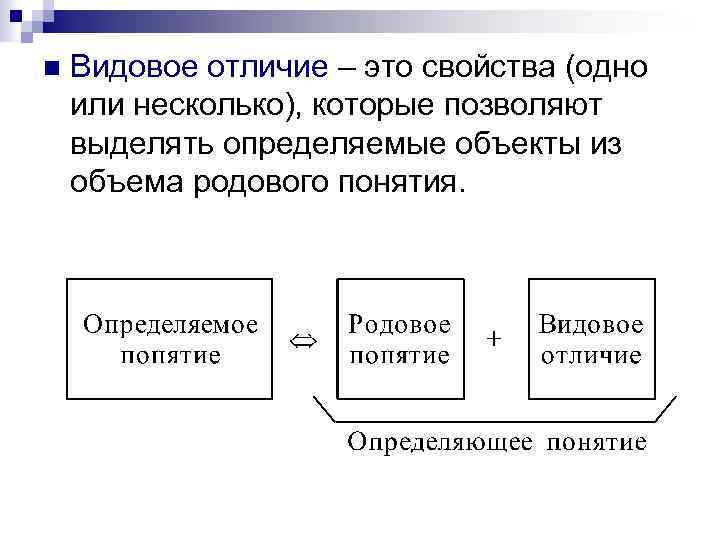n Видовое отличие – это свойства (одно или несколько), которые позволяют выделять определяемые объекты из объема родового понятия.

Формулируя определения понятий через род и видовое отличие, придерживаются ряда правил: 1. 2. 3. 4. Определение должно быть соразмерным. Это означает, что объемы определяемого и определяющего понятий должны совпадать. Это правило вытекает из того, что определяемое и определяющее понятия взаимозаменяемы. В определении не должно быть порочного круга. Это означает, что нельзя определять понятие через само себя (в определяющем не должно содержаться определяемого термина) или определять его через другое, которое, в свою очередь, определять через него. Определение должно быть ясным. Это на первый взгляд очевидное правило, но означает оно многое. Прежде всего, требуется, чтобы значения терминов, входящих в определяющее понятие, были известны к моменту введения определения нового понятия. Одно и то же понятие определить через род и видовое отличие, соблюдая сформулированные выше правила, можно по-разному.

Последовательность действий, которую нужно соблюдать, если воспроизводить определение знакомого понятия или построить определение нового: 1. 2. 3. 4. Назвать определяемое понятие (термин). Указать ближайшее родовое (по отношению к определяемому) понятие. Перечислить свойства, выделяющие определяемые объекты из объема родового, т. е. сформулировать видовое отличие. Проверить, выполнены ли правила определения понятия

n n n При изучении математики в начальной школе чаще всего используют неявные определения. В неявных определениях содержание понятий раскрывается косвенным путем. Среди них различают контекстуальные и остенсивные. В контекстуальных определениях содержание нового понятия раскрывается через отрывок текста, через контекст, через анализ конкретной ситуации, описывающей смысл вводимого понятия. Посредством контекста устанавливается связь определяемого понятия с другими, известными, и тем самым косвенно раскрывается его содержание.

+ 6 = 15 0, 5, 9, 10 К какому числу надо прибавить 6, чтобы получилось 15? Обозначим неизвестное число латинской буквой x (икс): x + 6 = 15 – это уравнение. Решить уравнение – значит найти неизвестное число. В данном уравнении неизвестное число равно 9, так как 9 + 6 = 15. Объясни, почему числа 0, 5 и 10 не подходят?

Остенсивные определения – это определения, раскрывающие существенные признаки предметов путем их указания, показа. Они используются для введения терминов путем демонстрации объектов, которые этими терминами обозначают. Например, таким способом можно определить в начальной школе понятия равенства и неравенства: 2 7 > 2 6 9 3 = 27 78 – 9 < 78 6 4 = 4 6 37 + 6 > 37 17 – 5 = 8 + 4 Это неравенства. Это равенства.

n n В начальном обучении математике, кроме контекстуальных и остенсивных определений, часто используют приемы, заменяющие определение. Это, в частности, описание, сравнение. При описании изучаемого объекта ставится цель – выявить как можно больше его свойств как существенных, так и несущественных. Если используется прием сравнения, то свойства вводимого понятия выявляются в процессе сравнения различных объектов.

1. 2. 3. Деление понятия – это логическая операция, раскрывающая объем понятия. В процессе деления объем понятия (множество) разбивается на непересекающиеся подмножества (классы). При выполнении операции деления понятия надо соблюдать ряд правил: деление должно быть соразмерным, т. е. объем делимого понятия должен совпадать с объединением объемов членов деления; объемы членов деления не должны пересекаться; деление должно производиться только по одному признаку – основанию деления.