Мат основы КГ.pptx
- Количество слайдов: 36

Математические основы Компьютерной графики

Простые преобразования точек • Точка P на плоскости однозначно определяется двумя своими координатами (x, y). В соответствие ей можно поставить матрицу-строку размером 1 2 вида. Следует заметить также, что точка может задаваться и соответствующей матрицей-столбцом размером 2 1. В любом случае матрицу, определяющую положение точки, часто называют координатным вектором или вектором положения. Преобразования размером 2 2 вида :

• Рассмотренные приемы преобразования точки можно обобщить на аналогичные преобразования отрезков прямых и многоугольников (см. ниже). Вместе с тем, более сложные варианты преобразования, рассмотренные далее применительно к отрезкам и многоугольникам, можно использовать и для точек. • Отметим здесь еще только одно обстоятельство. Преобразование точки, находящейся в начале координат, с использованием матрицы преобразования приведенного выше вида дает однозначный результат: т. е. начало координат инвариантно относительно данного преобразования.

Простые преобразования отрезков прямых и многоугольников Отрезок прямой линии определяется координатами двух его концов: A (x 1 , y 1) и B (x 2 , y 2). Или двумя координатными векторами: Более компактно можно задать отрезок матрицей размером 2 2 вида Аналогичным образом многоугольник может быть представлен M 2 матрицей (где M – число вершин многоугольника), в строки которой в строгой последовательности занесены координаты его вершин, т. е. матрицей вида:
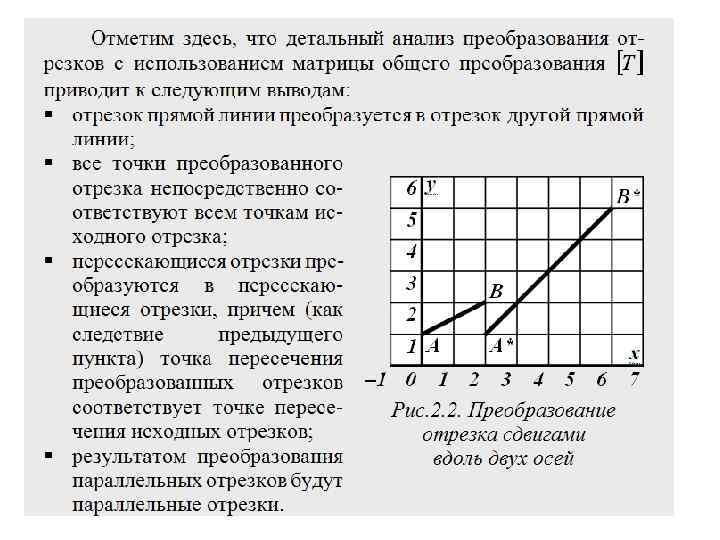

Поворот С помощью 2 2 матрицы общего преобразования можно организовать и повороты точек, отрезков и многоугольников относительно начала координат. В рассматриваемой системе координат при повороте в положительном направлении по правилу правой руки – против часовой стрелки на 90 , 180 и 270 применяют матрицы соответственно
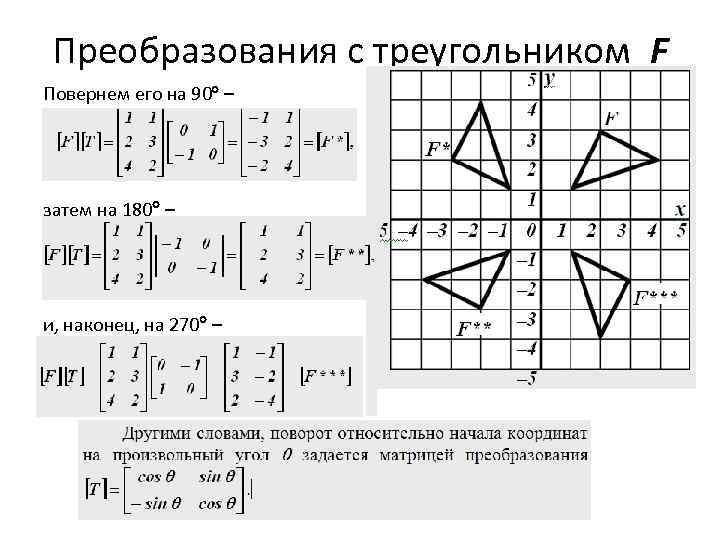
Преобразования с треугольником F Повернем его на 90 – затем на 180 – и, наконец, на 270 –

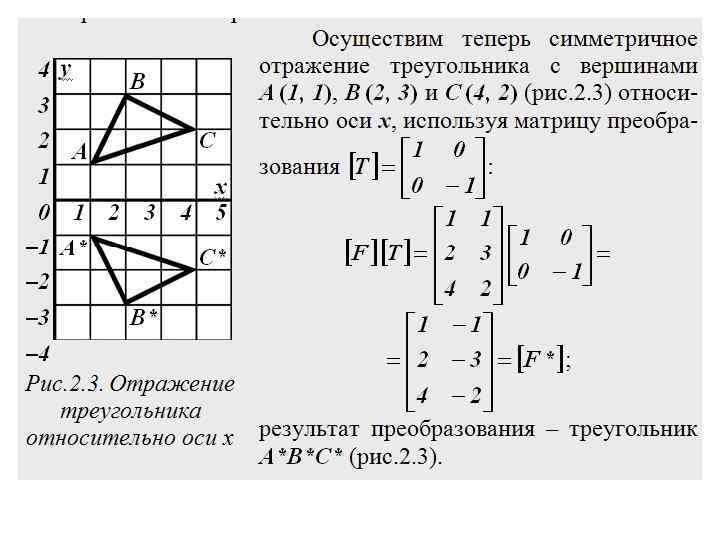
Отражение относительно прямых у = x и у = – x Как было установлено выше, симметричное отражение относительно оси x (прямой у = 0), относительно оси у (прямой x = 0) и относительно начала координат (точки с x = 0 и у = 0) можно осуществить, используя матрицы преобразования соответственно (последнее преобразование, кстати, идентично повороту на 180 ). Рассмотрим еще два вида симметричного отражения: относительно прямых у = x и у = – x. Они реализуются матрицами преобразования соответственно
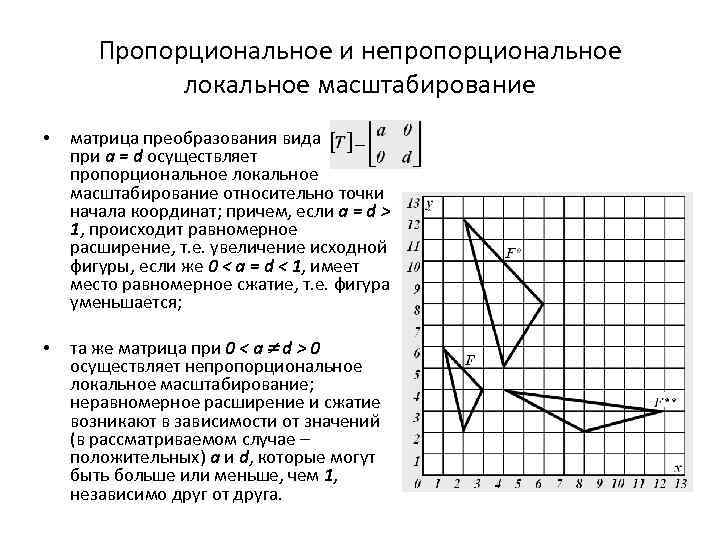
Пропорциональное и непропорциональное локальное масштабирование • матрица преобразования вида при a = d осуществляет пропорциональное локальное масштабирование относительно точки начала координат; причем, если a = d > 1, происходит равномерное расширение, т. е. увеличение исходной фигуры, если же 0 < a = d < 1, имеет место равномерное сжатие, т. е. фигура уменьшается; • та же матрица при 0 < a d > 0 осуществляет непропорциональное локальное масштабирование; неравномерное расширение и сжатие возникают в зависимости от значений (в рассматриваемом случае – положительных) a и d, которые могут быть больше или меньше, чем 1, независимо друг от друга.

Комбинированные преобразования

Перемещение Исследуем теперь дополнительные возможности, открывающиеся при новом подходе к преобразованиям. Проведем следующую матричную операцию:

Поворот вокруг произвольной точки • объект преобразования перемещается таким образом, чтобы точка, относительно которой совершается поворот, попала в начало координат; • выполняется поворот объекта на требуемый угол вокруг точки начала координат; • осуществляется обратное перемещение объекта так, чтобы точка центра вращения возвратилась на исходное место. Применительно координатному вектору точки [ x y 1 ] подобная операция поворота вокруг точки с координатами (m, n) на произвольный угол реализуется следующими матричными преобразованиями:

Проецирование в однородных координатах Матрицу общего преобразования для трехмерных координатных векторов, используемых при двумерных преобразованиях, в общем виде можно представить так: Ранее было установлено, как входящие в нее коэффициенты a, b, c, d, m и n влияют на соответствующие преобразования. Остальным трем коэффициентам в предыдущих разделах присваивались вполне определенные значения ( p = q = 0, s = 1), и они, по сути дела, не принимали участия в преобразованиях. Координатные векторы преобразованных точек всегда имели вид т. е. число h тождественно принимало единичное значение. Геометрически это можно трактовать как ограничение преобразований физической плоскостью h = 1 в трехмерном пространстве xyh. Вместе с тем, при других значениях коэффициентов p, q и s они также могут участвовать в преобразованиях.

Общее масштабирование • Можно рассматривать общее масштабирование как частный случай проецирования в однородных координатах; геометрический смысл данного преобразования аналогичен рассмотренному в предыдущем разделе – это проецирование в трехмерном пространстве xyh точки c координатами (x, y, s), принадлежащей плоскости h = s, на плоскость h = 1 по лучу, соединяющему эту точку с началом координат. В отличие от локального масштабирования (которое осуществляется коэффициентами a и d матрицы преобразования и может быть как пропорциональным, так и непропорциональным) масштабирование с использованием коэффициента s называют общим. Причем общее масштабирование всегда пропорционально (равномерно). • Очевидно, что результаты двух приведенных здесь возможных вариантов пропорционального масштабирования (локального и общего) будут идентичны при условии, что значение a = d (в первом варианте) будет равно (во втором варианте).

Структура матрицы общего преобразования Рассмотрев действие всех коэффициентов 3 3 матрицы общего преобразования, сделаем следующее заключение. Условно ее можно разбить на четыре части (подматрицы) – коэффициенты каждой подматрицы связаны с преобразованиями определенного типа, а именно: коэффициенты левой верхней 2 2 подматрицы (a, b, c и d ) – с операциями локального масштабирования, сдвига, отражения и поворота, коэффициенты левой нижней 1 2 подматрицы (m и n) – с перемещениями вдоль координатных осей, коэффициенты правой верхней 2 1 подматрицы ( p и q) – с проецированием в однородных координатах, правая нижняя 1 1 подматрица (коэффициент s) – задает общее масштабирование.

Точки бесконечности Однородные координаты вида отображают точку бесконечности, которая принадлежит лучу, идущему из начала координат и проходящему через точку (x, y). Приведем несколько характерных случаев расположения точек бесконечности: • однородные координаты вида [ x 0 0 ] отображают точку бесконечности, лежащую при условии, что x > 0, на положительной полуоси x, при условии, что x < 0 – на отрицательной; • однородные координаты вида [ 0 y 0 ] соответствуют точке бесконечности, принадлежащей при y > 0 положительной полуоси y, при y < 0 – отрицательной; • однородные координаты вида [ x y 0 ] при y = x отображают точку бесконечности, лежащую на прямой y = x, причем при x=y>0–в первом квадранте координатной плоскости xy, при x = y < 0 – в третьем ее квадранте; • однородные координаты вида [ x y 0 ] при y = – x соответствуют точке бесконечности, расположенной на прямой y = – x, причем при x > 0, y < 0 – в четвертом квадранте координатной плоскости xy, при x < 0, y > 0 – во втором ее квадранте.

ПРОСТРАНСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ • Точка – • Отрезок – • Многогранник –

При пространственных преобразованиях применяют матрицу общего преобразования размером 4 4. Обобщенно ее можно представить так: причем (по аналогии с двумерными преобразованиями) коэффициенты левой верхней 3 3 подматрицы (a, b, c, d, e, f, g, i и j ) связаны с операциями локального масштабирования, сдвига, отражения и поворота, коэффициенты левой нижней 1 3 подматрицы (l, m и n) – с перемещениями вдоль координатных осей, коэффициенты правой верхней 3 1 подматрицы ( p, q и r) – с проецированием в однородных координатах, правая нижняя 1 1 подматрица (коэффициент s) – задает общее масштабирование.
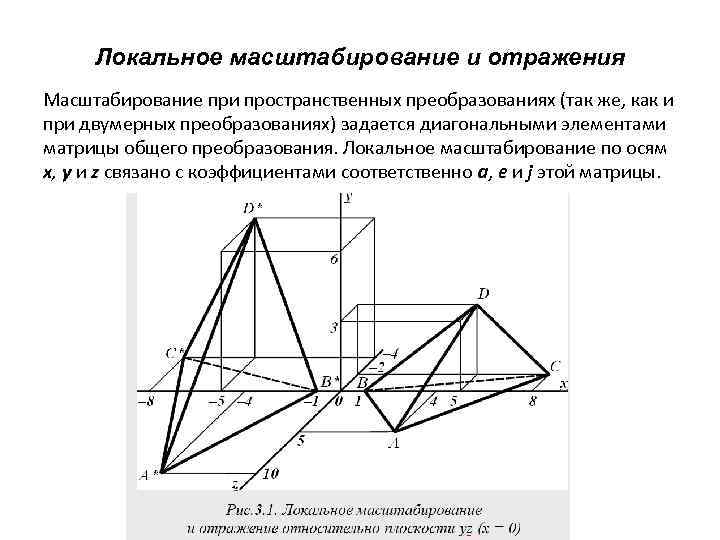
Локальное масштабирование и отражения Масштабирование при пространственных преобразованиях (так же, как и при двумерных преобразованиях) задается диагональными элементами матрицы общего преобразования. Локальное масштабирование по осям x, y и z связано с коэффициентами соответственно a, e и j этой матрицы.

Трехмерные сдвиги Сдвиги пространственных преобразованиях обусловливают недиагональные элементы левой верхней 3 3 подматрицы общего преобразования. Рассмотрим следующее преобразование точки: произошли сдвиги: вдоль оси x пропорционально координатам y (на dy) и z (на gz), вдоль оси y пропорционально координатам x (на bx) и z (на iz), вдоль оси z пропорционально координатам x (на сx) и y (на fy).

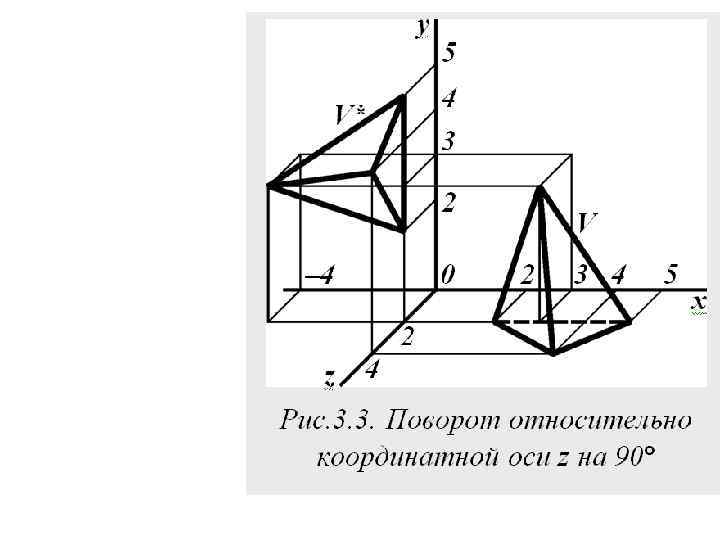
Повороты вокруг координатных осей При повороте графического объекта вокруг координатной оси x остаются неизменными x-координаты координатных векторов всех его точек. Приведем простой пример: поворот четырехгранника V (рис. 3. 3) на 90 относительно координатной оси z. Используя последнюю из приведенных выше трех матриц преобразования, получим: результат преобразования – четырехгранник V* (рис. 3. 3).

Поворот на произвольный угол вокруг прямой, параллельной координатной оси Реализация такого преобразования включает три последовательные простые операции: • перемещение объекта преобразования таким образом, чтобы прямая линия, относительно которой совершается поворот, совпала с той координатной осью, которой она параллельна (очевидно, что перемещение при этом осуществляется в общем случае вдоль двух других координатных осей на соответствующие расстояния); • поворот объекта на требуемый угол вокруг той координатной оси, с которой в предыдущем пункте совмещена прямая линия; • обратное перемещение объекта (на те же расстояния, что и в первом пункте, но в обратных направлениях).



Виды плоских геометрических проекций Трехмерные (объемные) сцены подлежат в большинстве случаев визуализации на двумерной поверхности (например, на экранной плоскости дисплея). При этом каждый трехмерный объект предварительно преобразуется, а именно проецируется на плоскость, называемую плоскостью проекции. Результат такого проецирования представляет собой плоскую геометрическую проекцию. По сути дела, каждая точка трехмерного объекта отображается на плоской геометрической проекции точкой, образованной пересечением прямой – она называется проектором, которая походит через соответствующую точку объекта и точку, называемую центром проекции. Все возможные варианты плоских геометрических проекций разделяются на две основные группы. К одной из них относятся так называемые параллельные проекции, к другой – перспективные проекции. Параллельная проекция образуется тогда, когда центр проекции расположен в бесконечности и все проекторы параллельны другу. В этом случае размер проекции отрезка прямой, например, не зависит от удаленности его концов от плоскости проекции, а определяется только взаимной ориентацией направляющего вектора самого отрезка, направления проецирования и плоскости проекции (и, конечно, размером исходного отрезка).

Перспективная (или центральная) проекция реализуется, когда центр проекции находится в конечной точке трехмерного пространства. На плоской перспективной проекции отображения параллельных прямых в общем случае не параллельны, они сходятся в одной точке (исключение составляет особый случай ориентации исходных прямых). Существует достаточно много видов параллельных и перспективных проекций. Так, среди параллельных проекций можно выделить ортографическую, аксонометрическую (в том числе триметрическую и ее частные случаи – диметрическую и изометрическую), а также косоугольную (в том числе кавалье и кабине) проекции. Перспективные проекции подразделяются на одноточечные, двухточечные и трехточечные.

Параллельные ортографические проекции Матрицы преобразования, которые позволяют рассчитать ортографические проекции трехмерных объектов (точнее – точки, концов отрезка или вершин многогранника) на координатные плоскости yz (x = 0), xz (y = 0) и xy (z = 0), выглядят соответственно так: Приведем пример формирования ортографических проекций четырехгранника V, изображенного на рис. 3. 8 а, с использованием данных матриц. Результаты преобразований будут следующими: для проекции на плоскость yz (рис. 3. 8 б) –
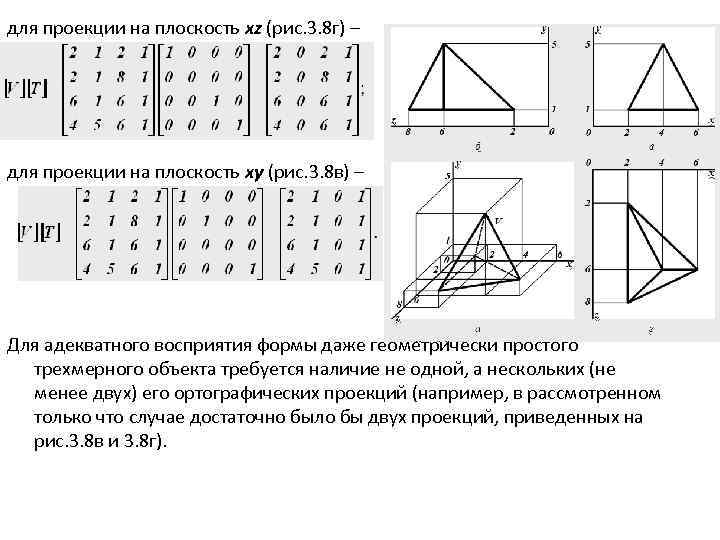
для проекции на плоскость xz (рис. 3. 8 г) – для проекции на плоскость xy (рис. 3. 8 в) – Для адекватного восприятия формы даже геометрически простого трехмерного объекта требуется наличие не одной, а нескольких (не менее двух) его ортографических проекций (например, в рассмотренном только что случае достаточно было бы двух проекций, приведенных на рис. 3. 8 в и 3. 8 г).

Перспективные одноточечные проекции Перспективное проецирование связано с ненулевыми значениями хотя бы одного из трех коэффициентов правой верхней 3 1 подматрицы общего преобразования размером 4 4, т. е. коэффициентов p, q и r. Такие композиции проецировании на плоскость yz (x = 0) с центром проекции на оси x, на плоскость xz (y = 0) с центром проекции на оси y и на плоскость xy (z = 0) с центром проекции на оси z будут выглядеть соответственно так:
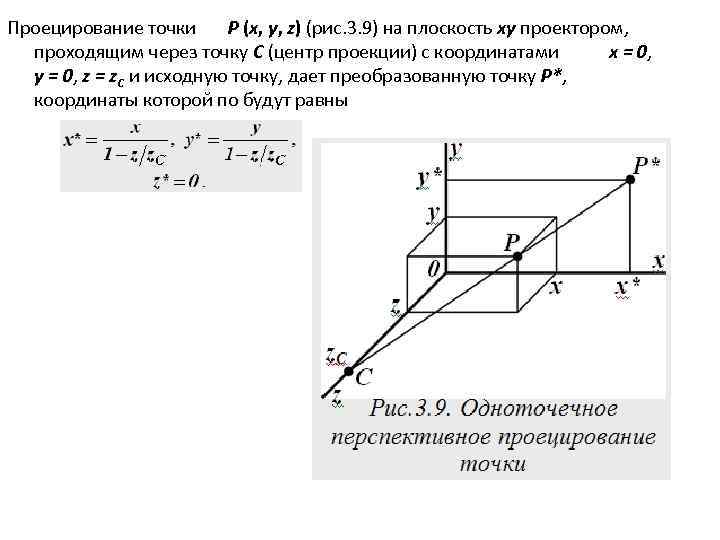
Проецирование точки P (x, y, z) (рис. 3. 9) на плоскость xy проектором, проходящим через точку C (центр проекции) с координатами x = 0, y = 0, z = z. C и исходную точку, дает преобразованную точку P*, координаты которой по будут равны

Чтобы лучше понять действие перспективного проецирования, рассмотрим тот же вариант преобразования применительно к отрезку AB (рис. 3. 10), параллельному координатной оси z, но поэтапно. Обозначим координаты концов отрезка A и B как соответственно (x 0, y 0, z 1) и (x 0, y 0, z 2) (на рис. 10 приведен отрезок с z 1 > 0 и z 2 < 0, что, впрочем, не имеет принципиального значения), сведем однородные координаты концов в матрицу [ L ] и осуществим первое преобразование – проецирование в однородных координатах при


Устремим конец В исходного отрезка в бесконечность в отрицательном направлении оси z, т. е. зададим при прочих равных условиях После проецирования в однородных координатах матрица с однородными координатами концов преобразованного отрезка (см. выше) будет выглядеть так: – точка бесконечности преобразована в точку начала координат.

Мат основы КГ.pptx