МАТЕМАТИЧЕСКИЕ ОСНОВЫ ГЕНЕРАЦИИ И ОБРАБОТКИ ИЗОБРАЖЕНИЙ ЛЕКЦИЯ

МАТЕМАТИЧЕСКИЕ ОСНОВЫ ГЕНЕРАЦИИ И ОБРАБОТКИ ИЗОБРАЖЕНИЙ ЛЕКЦИЯ 3 Зарецкий М. В. кафедра ВТи. ПМ

Простой пример • Рассмотрим рис. 1. Пусть заданы длина стрелы L 1, длина наконечника L 2, угол между каждой из сторон наконечника и «осью» стрелы Θ. • Чтобы нарисовать стрелу, надо задать координаты четырех точек (каких)? Как определить эти точки?

Рис. 1. Очень простая картинка. Стрела, расположенная вдоль оси абсцисс.

• Тот, кто решил поставленную задачу, без всякого труда сумеет построить такую же стрелу, с осью, расположенной вдоль оси ординат, а также стрелы, с осью, расположенной параллельно осям абсцисс и ординат. • А как быть, если ось стрелы, расположена не параллельно одной из координатных осей (рис. 2)? • Для решения подобных задач нам потребуется знание линейной алгебры и аналитической геометрии.

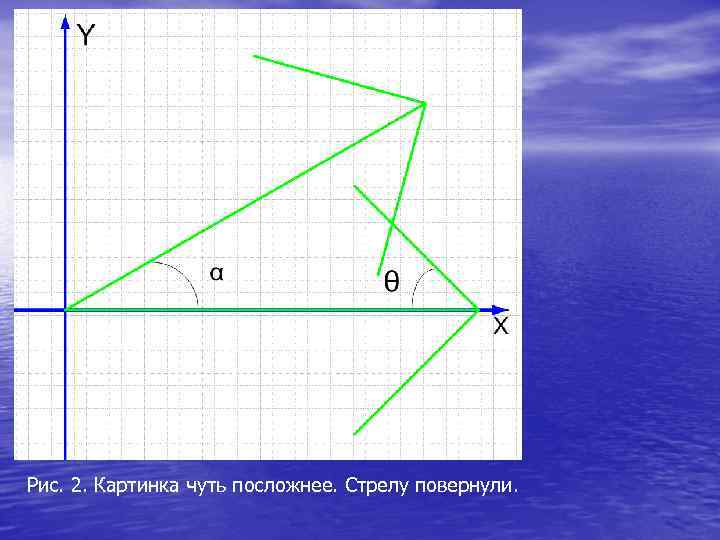
Рис. 2. Картинка чуть посложнее. Стрелу повернули.

Координатные системы • Разработчик или грамотный пользователь программных средств компьютерной графики должен понимать смысл геометрических преобразований, уметь создавать для них адекватную программную реализацию.

• Необходимо различать различные виды координат. Мировая система (в англоязычной литературе World Coordinate System — WCS) координат задается осями Xw, Yw, Zw. Мы размещаем ее в некоторой точке, и она всегда остается неподвижной. Размеры объектов в данной системе координат обычно соответствуют их реальным размерам.

• Вторая — система координат наблюдателя. Эту систему назовем Xe, Ye, Ze. Она определяет положение наблюдателя в пространстве и задает направление взгляда. И третья — система координат объекта XOb, YOb, ZOb. • . Наконец, нам требуется выводить графику на монитор, следовательно, нужна еще одна координатная система — X S, Y S.

• Рассмотрим задачу визуализации процесса прокатки. Мы можем привязать мировую систему координат к прокатному стану. Система координат наблюдателя будет характеризовать картину, которую видит оператор стана. Нам необходимо фиксировать состояние заготовки (процессы обжатия, вытяжки, уширения).

• Наконец, нам необходимо выводить изображение на монитор. Разумеется, в более сложной системе необходимо обращать внимание еще и на валки, приводы и т. д.

Рис. 3. Лабораторный прокатный стан (макет).

Рис. 4. Прокатный стан

• Для того, чтобы увидеть трехмерный объект на экране компьютера надо проделать следующие шаги: • - преобразовать координаты объекта, заданные в собственной системе координат, в мировые координаты; • - преобразовать координаты объекта, заданные уже в мировой системе координат, в систему координат наблюдателя;

• - спроецировать полученные координаты на проекционную плоскость в системе координат наблюдателя; • - перенести проекцию на монитор с соответствующим масштабированием. • Отметим один эффект. Мы находимся в поезде и смотрим в окно на другой поезд. Часто при плавном начале движения бывает непросто понять, какой из поездов поехал: «наш» в своем направлении или соседний — в противоположном.

• Кстати, если мы свяжем со «своим» поездом неподвижную систему координат, то «поедут» вокзалы, леса и поля. В компьютерной графике такой подход может оказаться вполне уместным.

Аффинные преобразования на плоскости • Пусть на плоскости введена прямоугольная система координат. • Каждой точке M на плоскости ставится в соответствие упорядоченная пара чисел (x, y), которые являются ее координатами. • Введя на плоскости еще одну систему координат, мы ставим в соответствие той же точке другую пару чисел (x’, y’).

• Переход от одной прямоугольной координатной системы на плоскости к другой описывается следующими формулами: • x’ = αx + βy + λ, • y’ = γx + δy + μ. • При этом должно выполняться: • αδ – βγ ≠ 0 •

• Свойства аффинных преобразований: • - y каждого аффинного преобразования есть обратное; • - прямые линии переводятся аффинным преобразованием в прямые линии; • - параллельность при аффинном преобразовании сохраняется.

• Отметим, что мы можем рассматривать аффинное преобразование и как изменение координат точки при переходе к новой системе координат, и как перемещение точки в неизменной системе координат. • Рассмотрим частные случаи аффинных преобразований.

Перенос • Математически перенос на вектор с компонентами (λ, μ) можно описать с помощью следующих формул: • x’ = 1 x + 0 y + λ, • y’ = 0 x + 1 y + μ. •

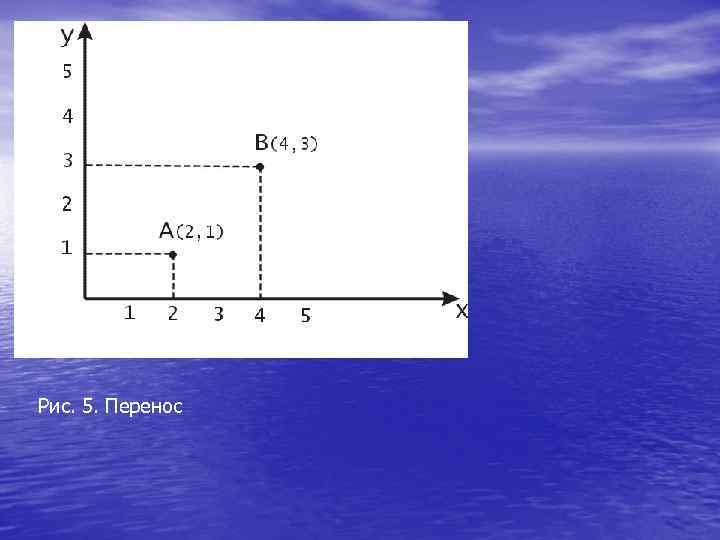
Рис. 5. Перенос

Масштабирование (растяжение, сжатие) • Математически масштабирование можно описать с помощью следующих формул: • x’ = α x + 0 y + 0, • y’ = 0 x + δy + 0. • α>0, δ>0

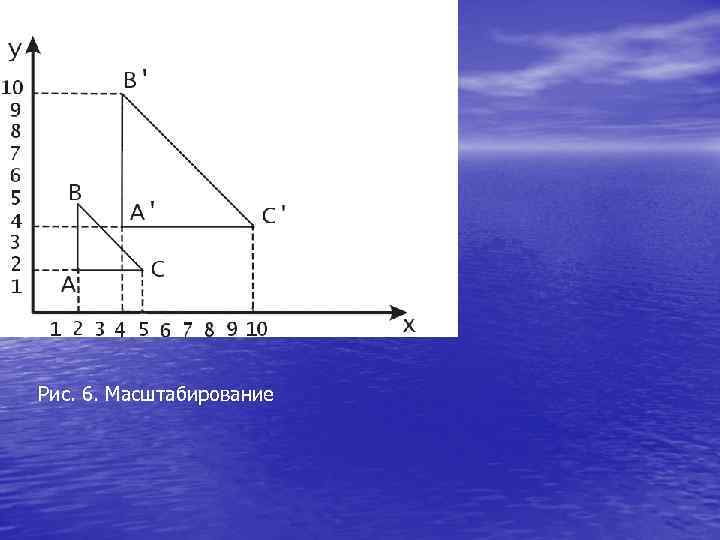
Рис. 6. Масштабирование

Вращение (поворот) • На рис. 7 точка A(x, y) переходит в точку B(x’, y’) поворотом вокруг начала координат на угол α. • Найдем формулы для математического описания данного преобразования. •

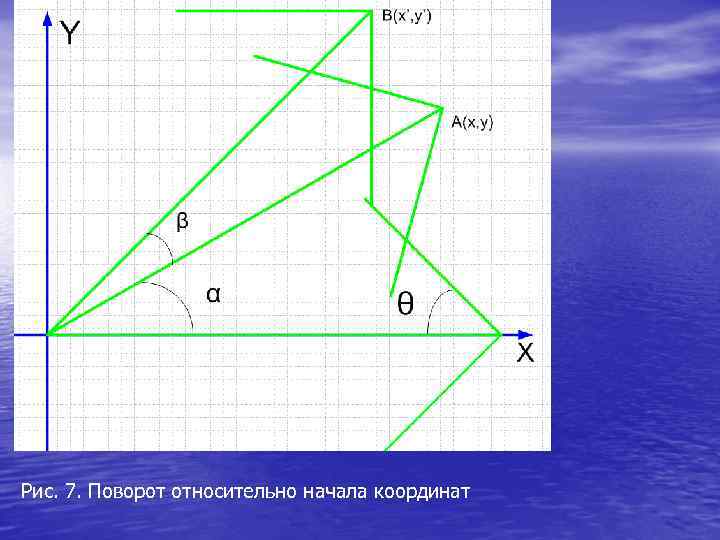
Рис. 7. Поворот относительно начала координат

• Мы видим, что первоначально стрела была повернута на угол α относительно оси абсцисс, затем был выполнен поворот на угол β. Таким образом, угол поворота относительно оси абсцисс равен • α+β • Вспомним, что длина стрелы равна L 1.

• Следовательно, • x’ = L 1 cos(α + β), • y’ = L 1 sin(α + β). • Выполнив элементарные тригонометрические преобразования, получим: • x’ = L 1(cosαcosβ - sinαsinβ), • y’ = L 1(sinαcosβ + cosαsinβ).

• Поскольку • x=L 1 cosα, y = L 1 sinα, • получаем: • x’ = xcosβ - ysinβ, • y’ = ycosβ + xsinβ. • В более общем виде получим: • x’ = xcosβ – ysinβ + 0, • y’ = xsinβ + ycosβ +0.

Зеркальное отражение • Для отражения относительно оси ординат получим следующие формулы: • x’ = -1 x + 0 y +0, • y’ = 0 x + 1 y +0. • Формулу для отражения относительно оси абсцисс приводить не будем.

• Как объяснить выбор именно этих операций? Во-первых, каждая из ни имеет простой и наглядный геометрический смысл. Во-вторых, в курсе аналитической геометрии доказывается, что любое аффинное преобразование сводится к последовательности (суперпозиции) приведенных простейших операций.

Матричная запись аффинных преобразований Растяжение (сжатие). Зеркальное отражение относительно оси ординат. Поворот.

• Естественно, возникает вопрос, как быть с преобразованием переноса. Ясно, что его таким же простым и удобным способом описать невозможно. Для того, чтобы сформулировать способ, позволяющий создать универсальное описание аффинных преобразований на плоскости, нам необходимо ввести в рассмотрение однородные координаты.

Однородные координаты точек на плоскости • Пусть — M произвольная точка плоскости с координатами (x, y). Однородными координатами этой точки называется любая тройка одновременно не равных нулю чисел x 1, x 2, x 3, связанных с заданными x и y соотношениями: x 1/x 3 = x, x 2/x 3 = y.

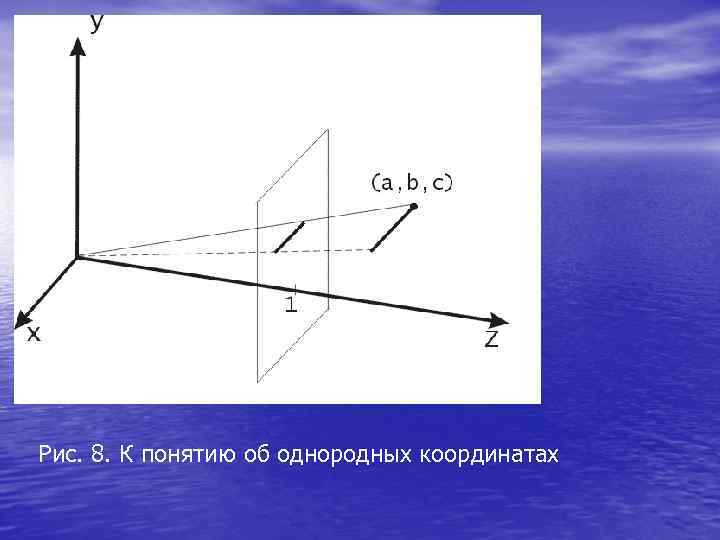
Рис. 8. К понятию об однородных координатах

• Рассмотрим точку трехмерного пространства (a, b, c) (см. рис. 8) и прямую, проходящую через начало координат и эту точку. Эта прямая пересечется с плоскостью z = 1 в точке с координатами (a/c, b/c, 1). Произвольная точка на той же прямой имеет координаты (wa/c, wb/c, w). • Очевидно, что любая точка прямой, соединяющей начало координат с точкой (x, y, 1) , может быть задана тройкой чисел (wx, wy, w).

• Будем считать, что w ≠ 0. Вектор с координатами (wx, wy, w) является направляющим вектором прямой, соединяющей точки (0, 0, 0) и (x, y, 1). Эта прямая пересекает плоскость z = 1 в точке , которая однозначно определяет точку (x, y) координатной плоскости x, y.

• Тем самым между произвольной точкой с координатами (x, y) и множеством троек чисел вида (wx, wy, w) , w ≠ 0 установлено взаимно однозначное соответствие, позволяющее считать числа wx, wy, w координатами точки. Эквивалентность таких троек чисел будем обозначать таким образом: • (wx, wy, w) ~ (x, y, 1) , w ≠ 0

Перенос. Матрица переноса. Вращение (поворот). Матрица вращения (поворота).

Задания • 1. Вывести матрицы для зеркального отражения и растяжения (сжатия). • 2. Показать, что суперпозиция аффинных преобразований является аффинным преобразованием, а ее матрица является произведением матриц составляющих преобразований.

• 3. Проверить являются ли аффинными преобразования введенные на кадре 17. • 4. Выяснить зависит ли результат выполнения подряд нескольких аффинных преобразований от порядка, в котором они выполняются. • 5. Установить, как изменится запись аффинных преобразований и их суперпозиции при переходе от векторов -строк к векторам-столбцам.