Скачать презентацию Математические операции над случайными величинами Независимые случайные Скачать презентацию Математические операции над случайными величинами Независимые случайные

Непрерывные случайные величины[1].ppt

  • Количество слайдов: 58

Математические операции над случайными величинами Математические операции над случайными величинами

Независимые случайные величины Две случайные величины называются независимыми, если закон распределения одной из них Независимые случайные величины Две случайные величины называются независимыми, если закон распределения одной из них не меняется от того, какие возможные значения приняла другая величина. Так, если дискретная случайная величина Х может принимать значения хi (i=1, 2, …, n), а случайная величина Y – значения yj (j=1, 2, …, m), то независимость дискретных случайных величин Х и Y означает независимость событий Х = хi и Y= yj при любых i=1, 2, …, n и j=1, 2, …, m. В противном случае случайные величины называются зависимыми.

Математические операции над дискретными случайными величинами Пусть даны 2 случайные величины Произведением k. Х Математические операции над дискретными случайными величинами Пусть даны 2 случайные величины Произведением k. Х случайной величины X на постоянную величину k называется случайная величина, которая принимает значения kxi с теми же вероятностями pi (i = 1, 2, . . . , n). m-й степенью случайной величины X, т. е. Xm , называется случайная величина, которая принимает значения xim с теми же вероятностями pi (i = 1, 2, . . . , n).

Математические операции над дискретными случайными величинами Суммой (разностью или произведением) случайных величин X и Математические операции над дискретными случайными величинами Суммой (разностью или произведением) случайных величин X и Y называется случайная величина, которая принимает все возможные значения вида xi+yj (xi-yj или xi∙yj ), где i=1, 2, . . . , n; j=1, 2, …, m с вероятностями рij того, что случайная величина X примет значение хi , a Y — значение уj: Если случайные величины X и Y независимы, т. е. независимы любые события Х = хi и Y= yj то по теореме умножения вероятностей для независимых событий

Непрерывные случайные величины Непрерывные случайные величины

Определение непрерывной случайной величины Непрерывной называется случайная величина ξ, функцию распределения F(x) которой можно Определение непрерывной случайной величины Непрерывной называется случайная величина ξ, функцию распределения F(x) которой можно представить в виде Функция φ(х) называется плотностью распределения (вероятностей) случайной величины ξ

Определение непрерывной случайной величины Плотность распределения φ(х) представляет собой производную функции распределения F(x) Определение непрерывной случайной величины Плотность распределения φ(х) представляет собой производную функции распределения F(x)

Свойства плотности распределения 1. Т. к. , а функция распределения неубывающая дифференцируемая функция Свойства плотности распределения 1. Т. к. , а функция распределения неубывающая дифференцируемая функция

Свойства плотности распределения 2. Т. к. , то в силу определения непрерывной случайной величины Свойства плотности распределения 2. Т. к. , то в силу определения непрерывной случайной величины Таким образом, вероятность попадания случайной величины на интервал численно равна площади криволинейной трапеции

Свойства плотности распределения 3. т. к. , то событие является достоверным Площадь, целиком заключенная Свойства плотности распределения 3. т. к. , то событие является достоверным Площадь, целиком заключенная под всей кривой, изображающей плотность распределения, равна 1.

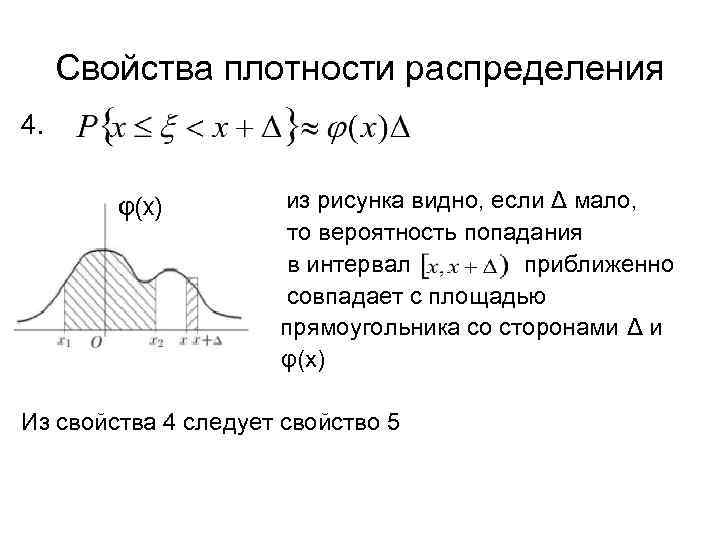Свойства плотности распределения 4. из рисунка видно, если Δ мало, то вероятность попадания в Свойства плотности распределения 4. из рисунка видно, если Δ мало, то вероятность попадания в интервал приближенно совпадает с площадью прямоугольника со сторонами Δ и φ(х) Из свойства 4 следует свойство 5

Свойства плотности распределения 5. Т. е. вероятность попадания в любую точку для непрерывной случайной Свойства плотности распределения 5. Т. е. вероятность попадания в любую точку для непрерывной случайной величины равна нулю. Из свойства 5 следует, что в свойствах 2, и 4 знак ≤ можно заменить на <. 2`. 4`.

Основные законы распределения непрерывных случайных величин Основные законы распределения непрерывных случайных величин

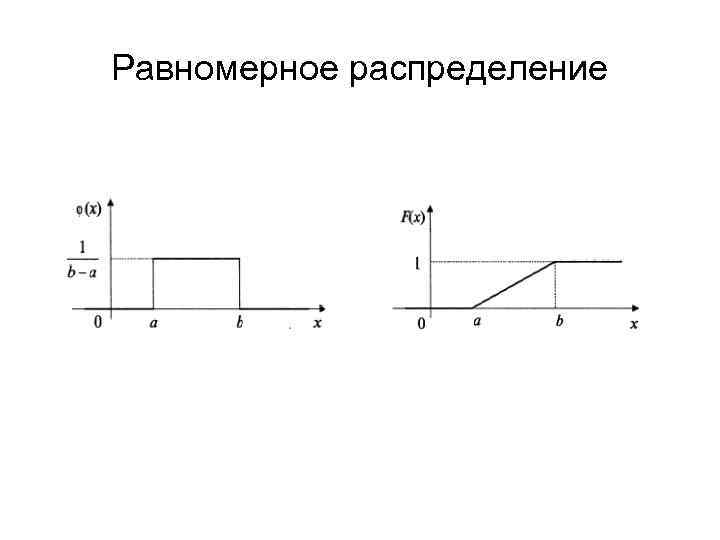
Равномерное распределение Непрерывная случайная величина X имеет равномерный закон распределения на отрезке [а, b], Равномерное распределение Непрерывная случайная величина X имеет равномерный закон распределения на отрезке [а, b], если ее плотность вероятности φ(х) постоянна на этом отрезке и равна нулю вне его, т. е. Функция распределения случайной величины X, распределенной по равномерному закону, есть

Равномерное распределение • При функция распределения Равномерное распределение • При функция распределения

Равномерное распределение Равномерное распределение

Равномерное распределение • математическое ожидание • дисперсия Равномерное распределение • математическое ожидание • дисперсия

Равномерное распределение Равномерное распределение

Показательное (экспоненциальное) распределение Непрерывная случайная величина X имеет показательный (экспоненциальный) закон распределения с параметром Показательное (экспоненциальное) распределение Непрерывная случайная величина X имеет показательный (экспоненциальный) закон распределения с параметром X > 0, если ее плотность вероятности имеет вид: Функция распределения случайной величины X, распределенной по показательному (экспоненциальному) закону, есть

Показательное (экспоненциальное) распределение • При функция распределения Показательное (экспоненциальное) распределение • При функция распределения

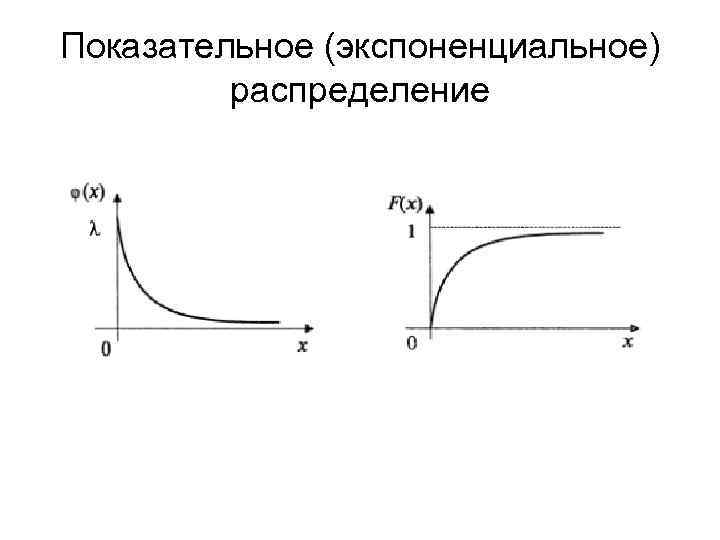
Показательное (экспоненциальное) распределение Показательное (экспоненциальное) распределение

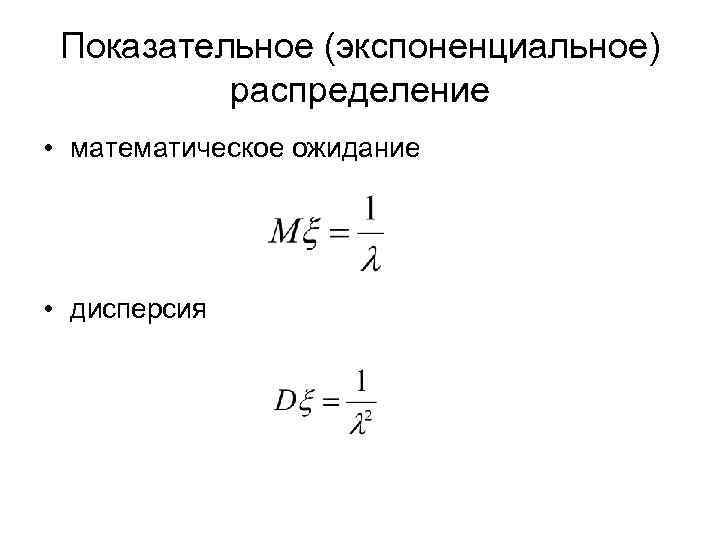Показательное (экспоненциальное) распределение • математическое ожидание • дисперсия Показательное (экспоненциальное) распределение • математическое ожидание • дисперсия

Показательное (экспоненциальное) распределение Показательное (экспоненциальное) распределение

Показательное (экспоненциальное) распределение Для вычисления дисперсии воспользуемся формулой Вычислим Показательное (экспоненциальное) распределение Для вычисления дисперсии воспользуемся формулой Вычислим

Показательное (экспоненциальное) распределение Таким образом Показательное (экспоненциальное) распределение Таким образом

Нормальное распределение Непрерывная случайная величина X имеет нормальный закон распределения (закон Гаусса) с параметрами Нормальное распределение Непрерывная случайная величина X имеет нормальный закон распределения (закон Гаусса) с параметрами а и σ2, если ее плотность вероятности имеет вид: Нормальное распределение определяется двумя параметрами а и σ, где а – математическое ожидание σ- среднее квадратическое отклонение

Нормальное распределение Нормальное распределение

Нормальное распределение Нормальное распределение

Нормальное распределение Исследуем функцию 1. Функция определена на всей оси х. 2. При всех Нормальное распределение Исследуем функцию 1. Функция определена на всей оси х. 2. При всех значениях х функция принимает положительные значения, т. е. график функции расположен над осью х. 3. т. е. ось Ох служит горизонтальной асимптотой графика. 4. При х=а функция имеет максимум Т. к. (экстремум функции)

Нормальное распределение 5. График функции симметричен относительно прямой х=а. 6. Точки графика токами перегиба. Нормальное распределение 5. График функции симметричен относительно прямой х=а. 6. Точки графика токами перегиба. т. к. являются

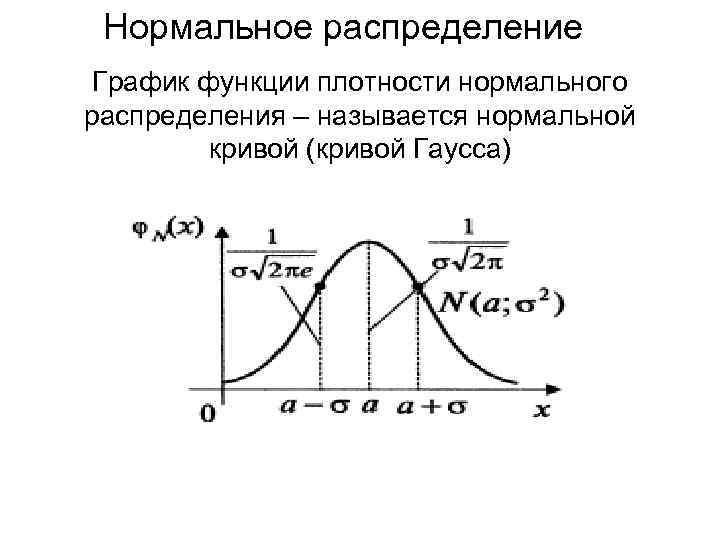Нормальное распределение График функции плотности нормального распределения – называется нормальной кривой (кривой Гаусса) Нормальное распределение График функции плотности нормального распределения – называется нормальной кривой (кривой Гаусса)

Нормальное распределение • Если σ=const, меняется только параметр а (а 1<a 2<a 3) – Нормальное распределение • Если σ=const, меняется только параметр а (а 1

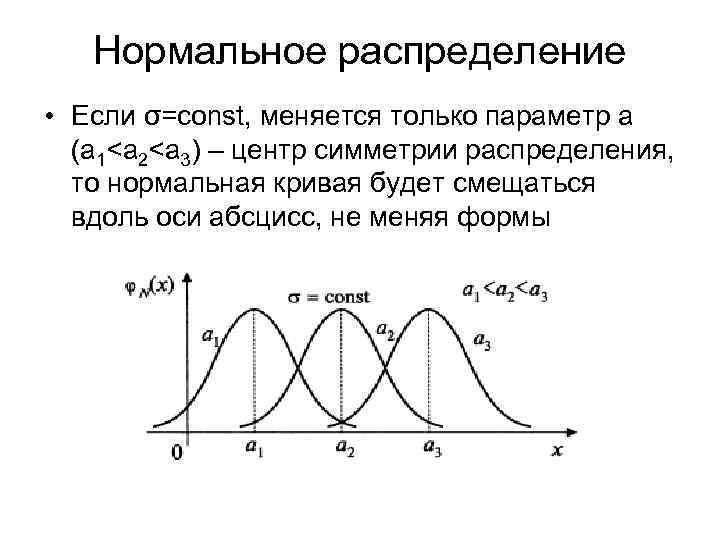
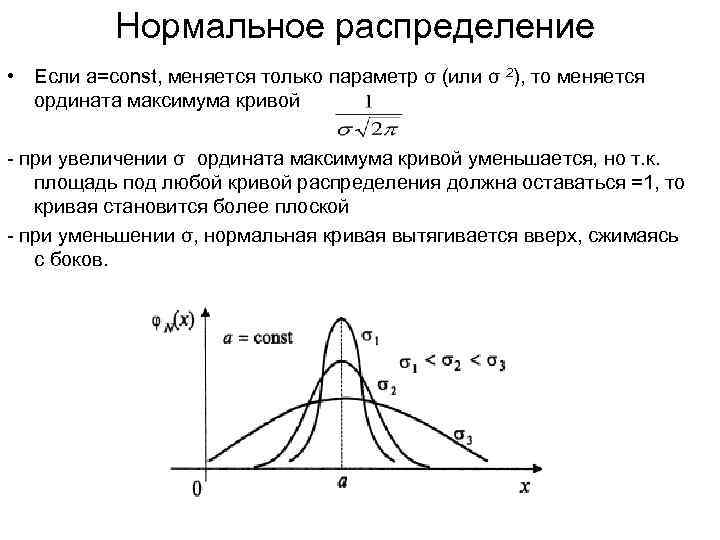Нормальное распределение • Если а=const, меняется только параметр σ (или σ 2), то меняется Нормальное распределение • Если а=const, меняется только параметр σ (или σ 2), то меняется ордината максимума кривой - при увеличении σ ордината максимума кривой уменьшается, но т. к. площадь под любой кривой распределения должна оставаться =1, то кривая становится более плоской - при уменьшении σ, нормальная кривая вытягивается вверх, сжимаясь с боков.

Нормальное распределение Таким образом, параметр а (математическое ожидание) характеризует положение центра, параметр σ 2 Нормальное распределение Таким образом, параметр а (математическое ожидание) характеризует положение центра, параметр σ 2 (дисперсия) — форму нормальной кривой. Нормальный закон распределения случайной величины с параметрами а=0, σ 2 =1, называется стандартным или нормированным, а соответствующая нормальная кривая — стандартной или нормированной.

Нормальное распределение Функция распределения случайной величины X, распределенной по нормальному закону, выражается через функцию Нормальное распределение Функция распределения случайной величины X, распределенной по нормальному закону, выражается через функцию Лапласа Ф(х) по формуле:

Нормальное распределение По определению функция распределения: Нормальное распределение По определению функция распределения:

Нормальное распределение Таким образом Нормальное распределение Таким образом

Нормальное распределение. Свойства случайной величины, распределенной по нормальному закону 1. Вероятность попадания случайной величины Нормальное распределение. Свойства случайной величины, распределенной по нормальному закону 1. Вероятность попадания случайной величины X, распределенной по нормальному закону, в интервал [х1, Х 2], равна Учитывая, что вероятность Р(х1 ≤ X ≤ х2) есть приращение функции распределения на отрезке [х1, х2] и формулу для функции распределения, получим

Нормальное распределение. Свойства случайной величины, распределенной по нормальному закону Геометрическая интерпретация 1 свойства Нормальное распределение. Свойства случайной величины, распределенной по нормальному закону Геометрическая интерпретация 1 свойства

Нормальное распределение. Свойства случайной величины, распределенной по нормальному закону 2. Вероятность того, что отклонение Нормальное распределение. Свойства случайной величины, распределенной по нормальному закону 2. Вероятность того, что отклонение случайной величины X, распределенной по нормальному закону, от математического ожидания а не превысит величину Δ > 0 (по абсолютной величине), равна

Нормальное распределение. Свойства случайной величины, распределенной по нормальному закону Учитывая свойство 1, а также Нормальное распределение. Свойства случайной величины, распределенной по нормальному закону Учитывая свойство 1, а также свойство нечетности функции Лапласа, получим

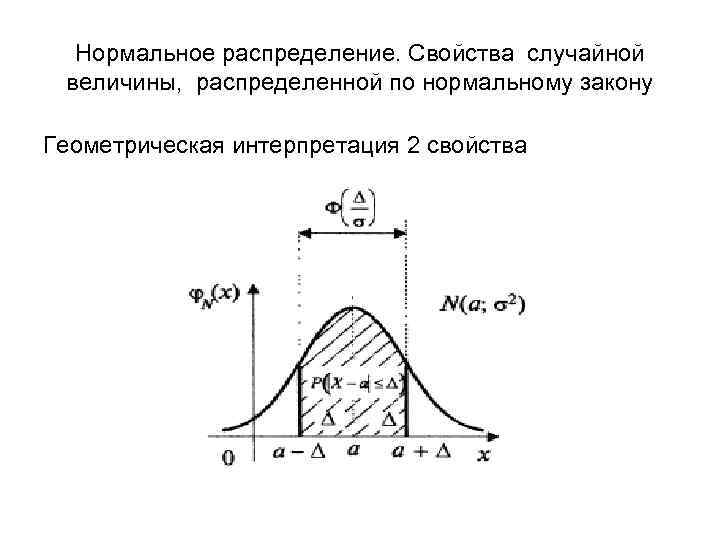Нормальное распределение. Свойства случайной величины, распределенной по нормальному закону Геометрическая интерпретация 2 свойства Нормальное распределение. Свойства случайной величины, распределенной по нормальному закону Геометрическая интерпретация 2 свойства

Нормальное распределение. «Правило трёх сигм» Используя 2 свойство вычислим вероятности Р(|X-a|≤Δ) при различных значениях Нормальное распределение. «Правило трёх сигм» Используя 2 свойство вычислим вероятности Р(|X-a|≤Δ) при различных значениях Δ (используя таблицу). Получим при «правило трех сигм» : Если случайная величина X имеет нормальный закон распределения с параметрами а и σ2, то практически достоверно, что ее значения заключены в интервале (а - З σ, а + З σ).

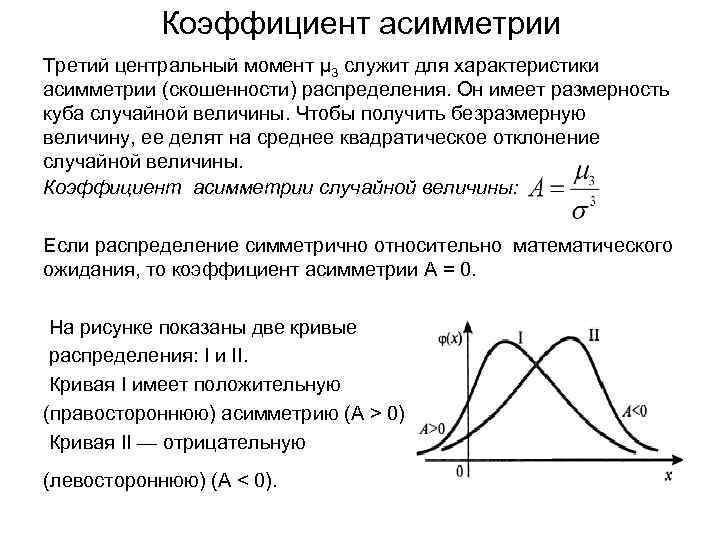Коэффициент асимметрии Третий центральный момент μ 3 служит для характеристики асимметрии (скошенности) распределения. Он Коэффициент асимметрии Третий центральный момент μ 3 служит для характеристики асимметрии (скошенности) распределения. Он имеет размерность куба случайной величины. Чтобы получить безразмерную величину, ее делят на среднее квадратическое отклонение случайной величины. Коэффициент асимметрии случайной величины: Если распределение симметрично относительно математического ожидания, то коэффициент асимметрии А = 0. На рисунке показаны две кривые распределения: I и II. Кривая I имеет положительную (правостороннюю) асимметрию (А > 0). Кривая II — отрицательную (левостороннюю) (А < 0).

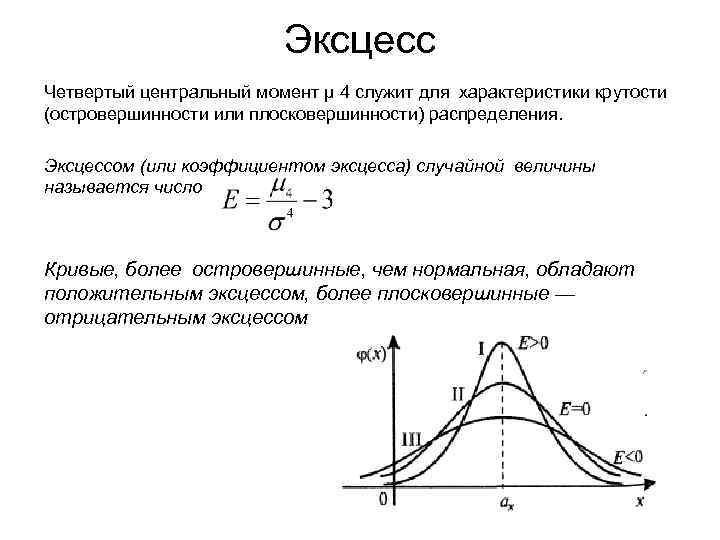Эксцесс Четвертый центральный момент μ 4 служит для характеристики крутости (островершинности или плосковершинности) распределения. Эксцесс Четвертый центральный момент μ 4 служит для характеристики крутости (островершинности или плосковершинности) распределения. Эксцессом (или коэффициентом эксцесса) случайной величины называется число Кривые, более островершинные, чем нормальная, обладают положительным эксцессом, более плосковершинные — отрицательным эксцессом

Коэффициент асимметрии и эксцесс случайной величины, распределенной по нормальному закону В силу симметрии нормальной Коэффициент асимметрии и эксцесс случайной величины, распределенной по нормальному закону В силу симметрии нормальной кривой относительно вертикальной прямой х=а, проходящей через центр распределения а = М(Х), коэффициент асимметрии нормального распределения А = 0. Эксцесс нормально распределенной случайной величины X найдем по формуле

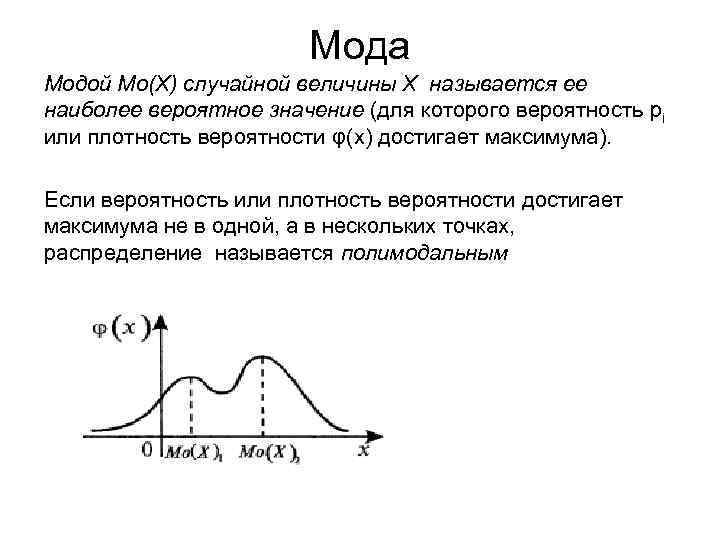Мода Модой Мо(Х) случайной величины X называется ее наиболее вероятное значение (для которого вероятность Мода Модой Мо(Х) случайной величины X называется ее наиболее вероятное значение (для которого вероятность рi или плотность вероятности φ(х) достигает максимума). Если вероятность или плотность вероятности достигает максимума не в одной, а в нескольких точках, распределение называется полимодальным

Медиана Медианой Ме(Х) непрерывной случайной величины X называется такое ее значение, для которого Р(Х Медиана Медианой Ме(Х) непрерывной случайной величины X называется такое ее значение, для которого Р(Х < Ме(Х)) = Р(Х > Ме(Х)) = ½. Вероятность того, что случайная величина X примет значение, меньшее медианы Ме(Х) или большее ее, одна и та же и равна 1/2. Геометрически вертикальная прямая х=Ме(Х), проходящая через точку с абсциссой, равной Ме(Х), делит площадь фигуры под кривой распределения на две равные части.

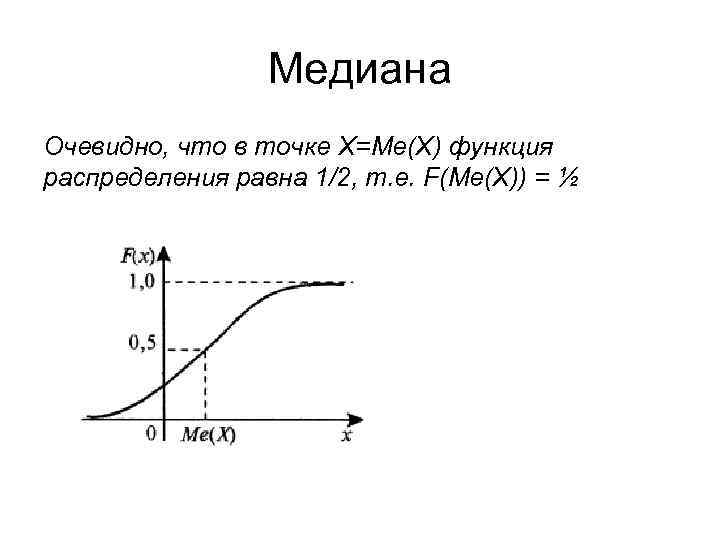Медиана Очевидно, что в точке Х=Ме(Х) функция распределения равна 1/2, т. е. F(Me(X)) = Медиана Очевидно, что в точке Х=Ме(Х) функция распределения равна 1/2, т. е. F(Me(X)) = ½

Логарифмически-нормальное распределение Непрерывная случайная величина X имеет логарифмически-нормальное (сокращенно логнормальное распределение), если ее логарифм Логарифмически-нормальное распределение Непрерывная случайная величина X имеет логарифмически-нормальное (сокращенно логнормальное распределение), если ее логарифм подчинен нормальному закону. Так как при х>0 неравенства X < х и In X< ln x равносильны, то функция распределения логнормального распределения совпадает с функцией нормального распределения для случайной величины In X, т. е. Дифференцируя F(х), получим выражение плотности вероятности для логнормального распределения

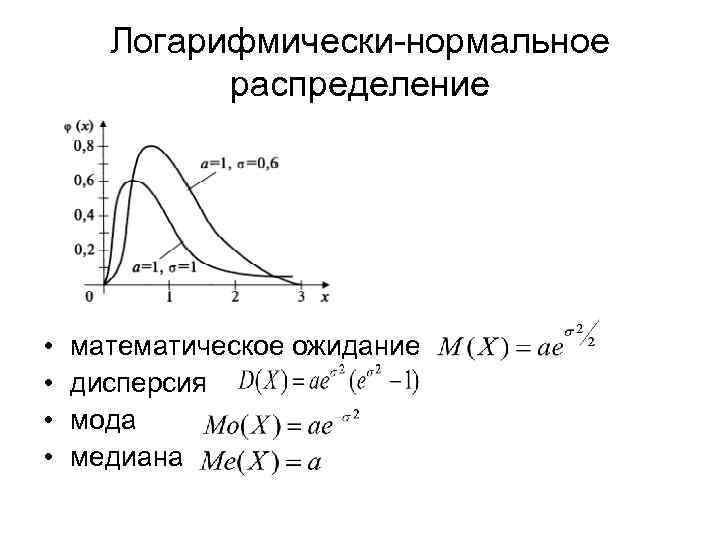Логарифмически-нормальное распределение • • математическое ожидание дисперсия мода медиана Логарифмически-нормальное распределение • • математическое ожидание дисперсия мода медиана

Распределение некоторых случайных величин, представляющих функции нормальных величин Распределение некоторых случайных величин, представляющих функции нормальных величин

-2א распределение Распределением ( 2א хи-квадрат) с k степенями свободы называется распределение суммы -2א распределение Распределением ( 2א хи-квадрат) с k степенями свободы называется распределение суммы квадратов к независимых случайных величин, распределенных по стандартному нормальному закону, т. е. где Zi(i = 1, 2, . . . , /; ) имеет нормальное распределение N(0; l). Плотность вероятности - 2א распределения имеет вид:

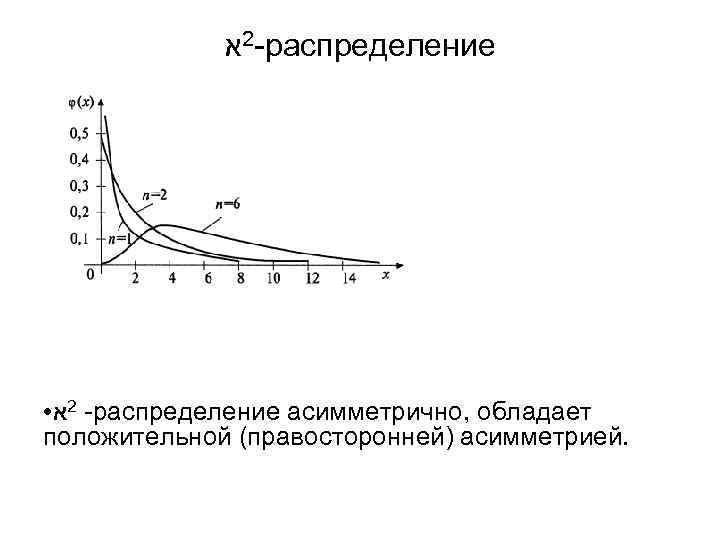-2א распределение - א распределение асимметрично, обладает положительной (правосторонней) асимметрией. ● 2 -2א распределение - א распределение асимметрично, обладает положительной (правосторонней) асимметрией. ● 2

Распределение Стьюдента Распределением Стьюдента (или t-распределением) называется распределение случайной величины где Z — случайная Распределение Стьюдента Распределением Стьюдента (или t-распределением) называется распределение случайной величины где Z — случайная величина, распределенная по стандартному нормальному закону, т. е. N(0; l); — 2א независимая от Z случайная величина, имеющая 2א распределение с k степенями свободы. где Г(у) — гамма- функция Эйлера в точке у.

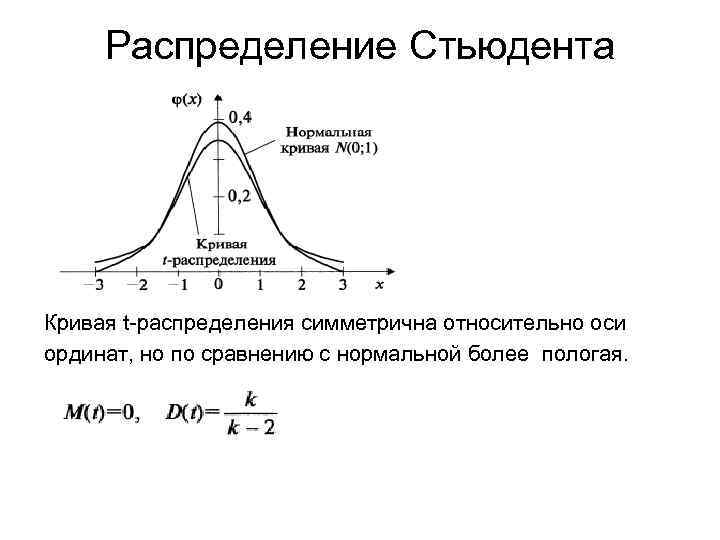Распределение Стьюдента Кривая t-распределения симметрична относительно оси ординат, но по сравнению с нормальной более Распределение Стьюдента Кривая t-распределения симметрична относительно оси ординат, но по сравнению с нормальной более пологая.

Распределение Фишера—Снедекора Распределением Фишера—Снедекора (или F-распределением) называется распределение случайной величины • случайные величины, имеющие Распределение Фишера—Снедекора Распределением Фишера—Снедекора (или F-распределением) называется распределение случайной величины • случайные величины, имеющие - 2א распределение с k 1 и k 2 степенями свободы. Плотность вероятности F-распределения имеет вид: где Г(у) — гамма- функция Эйлера в точке y.

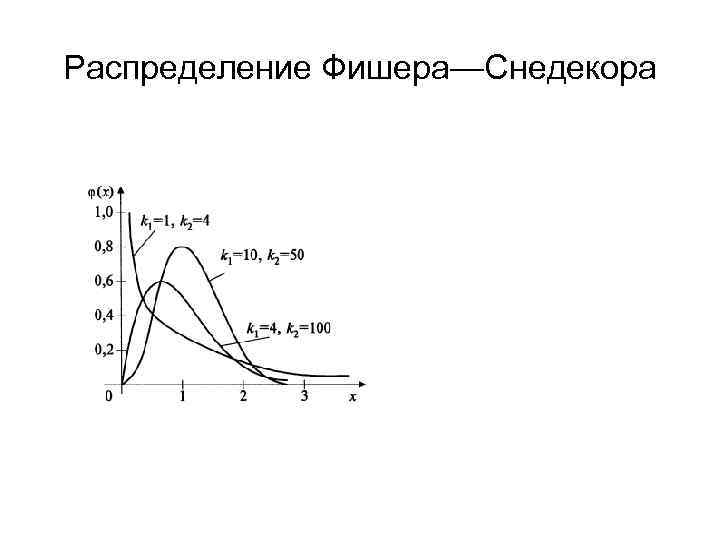Распределение Фишера—Снедекора Распределение Фишера—Снедекора