Математические модели систем управления Яркин

• Математические модели систем управления • Яркин • Примаков

Математическая модель – это совокупность математических соотношений, уравнений и неравенств, описывающих основные закономерности присущие изучаемому объекту или системе. • Для изучения и управления сложной физической системой необходимо получить её математическую модель.

С чего начинать при построении модели: 1) Определить систему и ее компоненты 2) Составить математическую модель и выдвинуть необходимые допущения. 3) Записать дифференциальные уравнения описывающие поведения модели. 4) Решить уравнения относительно желаемых выходных переменных. 5) Проанализировать решения и допущения. 6) При необходимости провести повторный анализ или синтез системы.

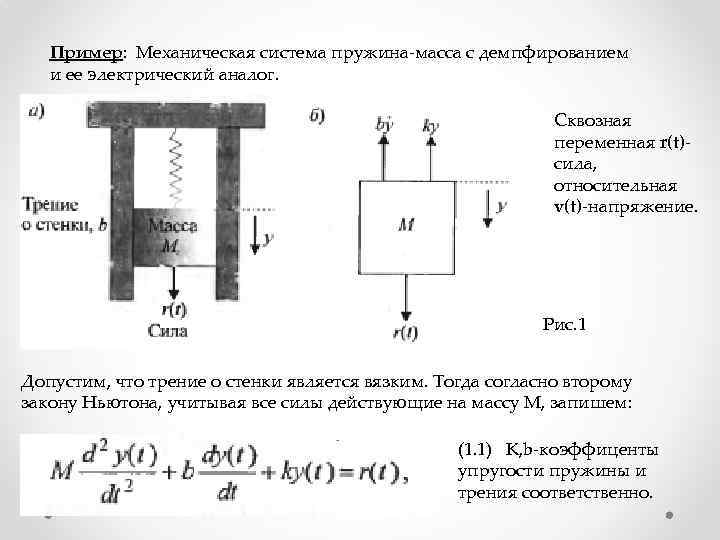Пример: Механическая система пружина-масса с демпфированием и ее электрический аналог. Сквозная переменная r(t)сила, относительная v(t)-напряжение. Рис. 1 Допустим, что трение о стенки является вязким. Тогда согласно второму закону Ньютона, учитывая все силы действующие на массу М, запишем: (1. 1) K, b-коэффиценты упругости пружины и трения соответственно.

Аналогом механической системы пружина масса, может являться RLC – цепь где сквозная переменная r(t)- обозначает ток, а относительная v(t)напряжение. (1. 2) С помощью законов Кирхгофа получим интегро-дифференциальное уравнение. (1. 3) Решим эти дифф. уравнения путем интегрирования с использованием неопределенных коэффициентов.

При нулевых начальных условиях y(t)=y(0), решение такой недодемпфированной системы будет описываться выражением: (1. 4) Аналог для RLC цепи, система находится под воздействием постоянного тока r(t)=I : (1. 5) Чтобы показать более близкое сходство между дифференциальными уравнениями механической и электрической систем, перепишем уравнение (1. 1) относительно скорости (1. 6)

В результате получим: (1. 7) (1. 3) Сравнивая (1. 7) с (1. 3) можем сделать вывод об эквивалентности этих уравнений, только в одном из них переменная v(t) обозначает напряжение, а в другом скорость. Данные переменные называют переменными аналогами, а соответствующие системы - подобными системами.

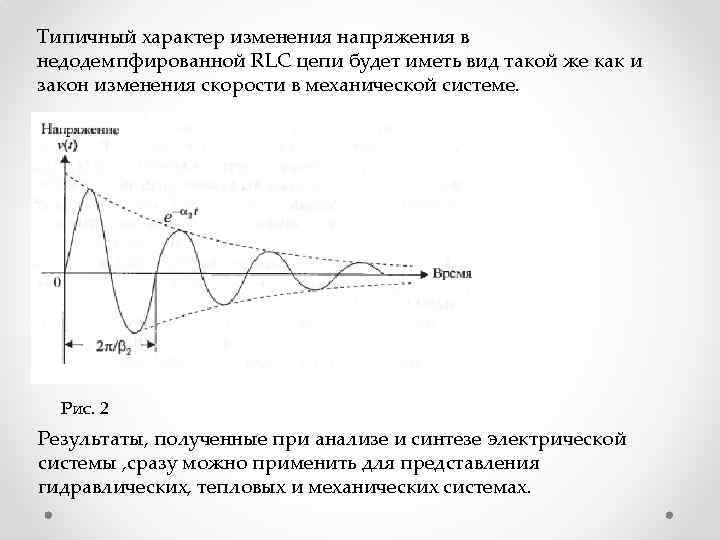Типичный характер изменения напряжения в недодемпфированной RLC цепи будет иметь вид такой же как и закон изменения скорости в механической системе. Рис. 2 Результаты, полученные при анализе и синтезе электрической системы , сразу можно применить для представления гидравлических, тепловых и механических системах.

Преобразование Лапласа • Метод преобразования Лапласа позволяет заменить сложное решение дифференциальных уравнений относительно простым решением алгебраических уравнений. • Для того, чтобы функция f(t) имела преобразование Лапласа, достаточно выполнения условия: (1. 8)

Все физически реализуемые сигналы имеют преобразование Лапласа. Преобразование Лапласа функции времени f(t) определяются выражением: (1. 9) Обратное преобразование Лапласа имеет вид: (1. 10) Переменную s в преобразования Лапласа можно рассматривать как оператор дифференцирования, т. е. (1. 11) оператор интегрирования: (1. 12)

Некоторые важные преобразования Лапласа (Дорф Р. Современные системы управления, стр. 64. ):

• Рассмотрим еще раз механическую систему, описываемую уравнением (1. 1): Нам необходимо получить решение этого уравнения, т. е. выражение y(t). Преобразование Лапласа уравнения (1. 1) имеет вид: (1. 13) Если , то получим: Выражая Y(s), получим: (1. 14)

Прировняв полином q(s) знаменателя получим характеристическое уравнение (его корни определяют характер движения системы). • Корни характеристического уравнения также называют полюсами системы. Корни полинома в числителе p(s) называют нулями системы. Пример: • Рассмотрим случай, когда k/M=2, b/M=3, следовательно выражение (1. 14) примет вид: (1. 15) • Положение полюсов и нуля этой функции на s – плоскости Рис. 3

• Разложив (1. 15) на элементарные дроби, получим: (1. 16) (1. 17) Рис. 4

• Графический способ нахождения вычетов имеет особую ценность в тех случаях, когда характеристическое уравнение имеет высокий порядок и когда некоторые полюсы образуют комплексносопряженные пары. • Преобразование Лапласа и использование s – является очень ценными методами анализа и синтеза систем, когда акцент делается на определение переходных режимов и точность в установившемся состоянии. Поскольку при исследовании систем управления в первую очередь представляет интерес именно два указанных фактора, то в связи с этим трудно переоценить метод преобразования Лапласа

Передаточные функции линейных систем • Передаточная функция линейной системы определяется как отношение преобразования Лапласа выходной переменной к преобразованию Лапласа входной переменной, при условии, что все начальные условия равны нулю. • Передаточная функция системы масса-пружина получается, если в исходном уравнении (1. 13) все начальные условия равны нулю: (1. 18)

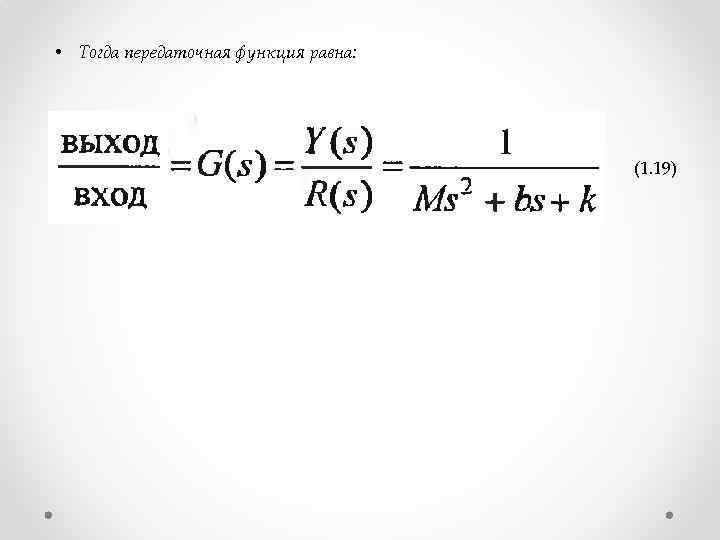• Тогда передаточная функция равна: (1. 19)

Пример Передаточной характеристики RC-цепи: • Уравнения Кирхгофа в операторной форме от-но напряжений: • Получим передаточную функцию системы: • τ = RC – постоянная времени цепи; • Полюс системы S(t)=-1/τ

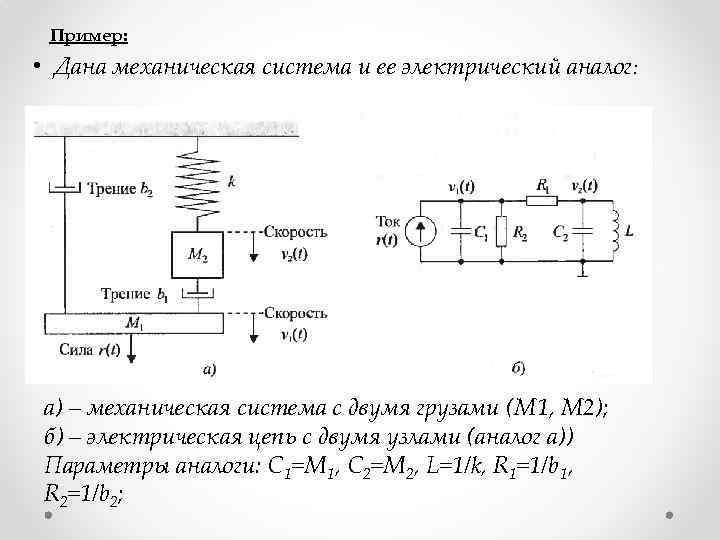Пример: • Дана механическая система и ее электрический аналог: а) – механическая система с двумя грузами (M 1, M 2); б) – электрическая цепь с двумя узлами (аналог a)) Параметры аналоги: С 1=М 1, С 2=М 2, L=1/k, R 1=1/b 1, R 2=1/b 2;

• Скорости v 1(t) и v 2(t) механической системы <=> напряжениям v 1(t) и v 2(t) в электрической цепи; • При нулевых начальных условиях, уравнения движения для механической системы, имеют вид: • Считая выходной переменной скорость массы M 1, выразим:

• Тогда передаточная функция механической (электрической) системы будет равна.

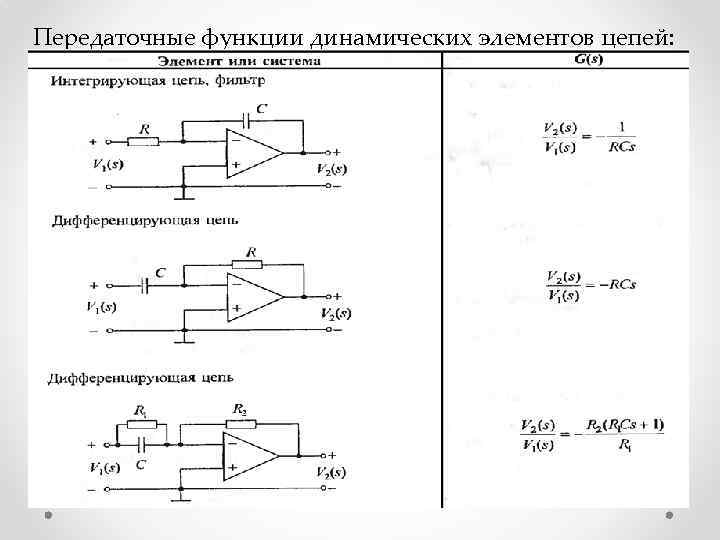Передаточные функции динамических элементов цепей:

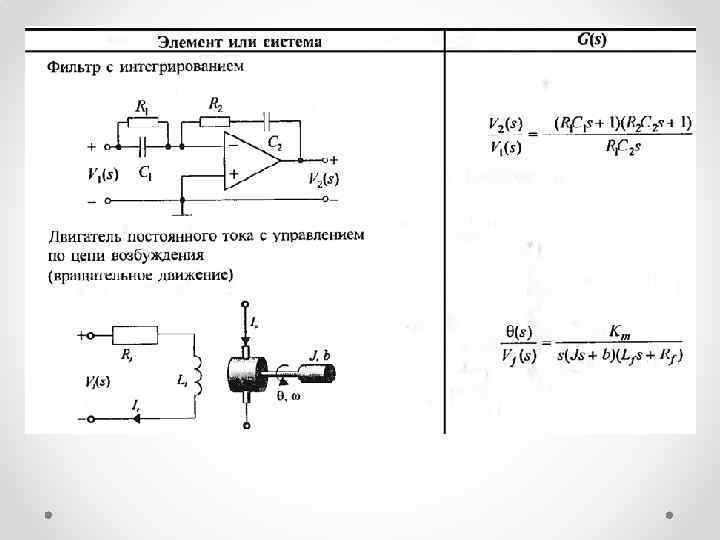
• Дорф Р. Современные системы управления, стр. 79.

Преимущество передаточной функции заключается в том, что она позволяет изобразить причинно-следственную связь между переменными в наглядной схематической форме, в теории управления преобладает представление различных динамических систем в виде структурных схем. Пример: Структурная схема двигателя постоянного тока: где Ѳ(s) – угол поворота, выходного вала двигателя, Vf(s) – напряжение питания. • Структурные схемы сложных систем можно упростить, сведя их схемы к конфигурации с меньшим числом блоков, чем в исходной системе.

• Для исходной структурной схемы: • Запишем передаточную функцию: • Преимущество передаточной функции заключается в том, что она позволяет изобразить причинно-следственную связь между переменными в наглядной схематической форме, в теории управления преобладает представление различных динамических систем в виде структурных схем.

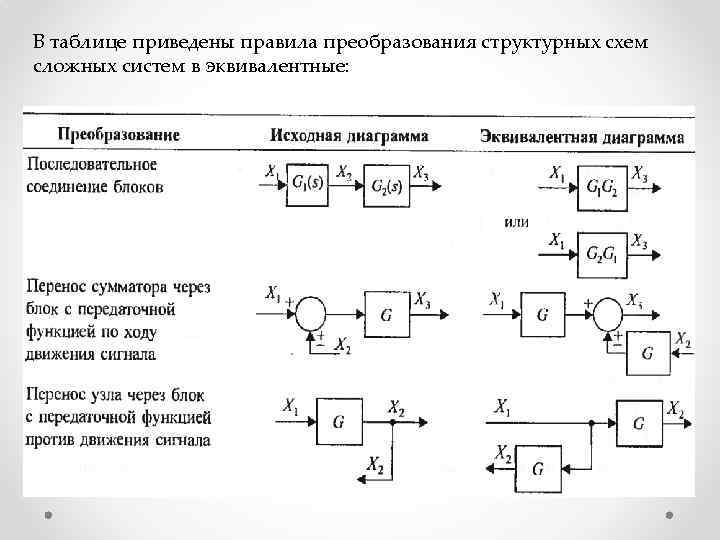В таблице приведены правила преобразования структурных схем сложных систем в эквивалентные:

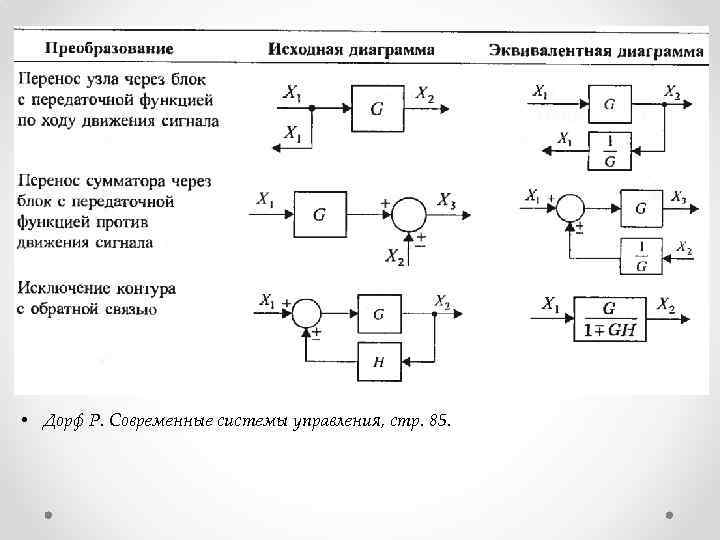• Дорф Р. Современные системы управления, стр. 85.

• Понятие передаточной функции и основанные на нем методы являются очень важными, поскольку они предоставляют в распоряжение исследователя и проектировщика столь ценное средство, как математическая модель элементов систем управления. • Преимущество передаточной функции заключается в том, что она позволяет изобразить причинно-следственную связь между переменными в наглядной схематической форме, в теории управления преобладает представление различных динамических систем в виде структурных схем.

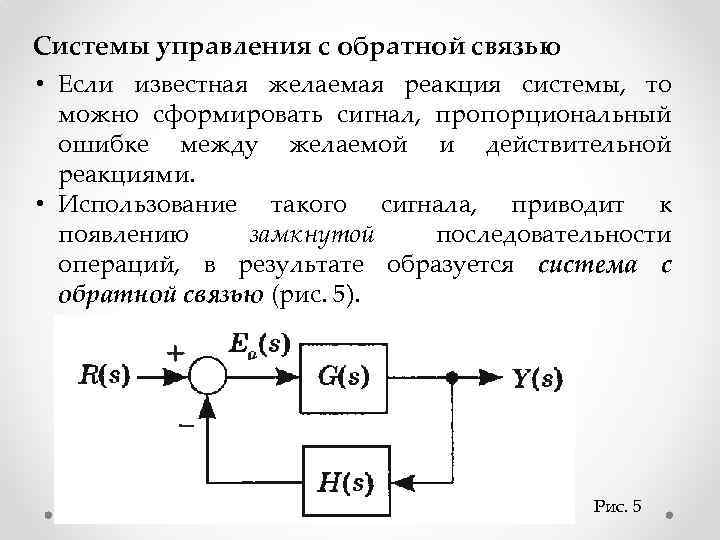Системы управления с обратной связью • Если известная желаемая реакция системы, то можно сформировать сигнал, пропорциональный ошибке между желаемой и действительной реакциями. • Использование такого сигнала, приводит к появлению замкнутой последовательности операций, в результате образуется система с обратной связью (рис. 5). Рис. 5

• При H(s)≠ 1, выход замкнутой системы равен: Сигнал ошибки:

Чувствительность систем управления Чувствительность системы – это соотношение изменения ее передаточной функции к изменениям передаточной функции (или параметров) объекта управления при условии их малости. Пусть система имеет передаточную функцию, тогда чувствительность определяется, как В пределе, переходя к малым изменениям, приводим к виду: (1. 20)

Из 1. 20 получим чувствительность для замкнутой системы. Пусть замкнутая система имеет передаточную функцию: • Следовательно, ее чувствительность равна: • Чувствительность замкнутой системы можно сделать меньше, чем ее чувствительность в разомкнутом состоянии, путем увеличения GH(s). • Чувствительность замкнутой системы к изменению передаточной функции элемента обратной связи H(s) равна:

• Если произведение GH велико, то чувствительность близка к 1. • В качестве элементов обратной связи необходимо выбирать такие, которые обладали бы стабильными характеристиками, не зависящими от внешних факторов. Таким образом, способность уменьшать влияние изменения параметров путем введения обратной связи – одно из положительных качеств замкнутых систем управления. • Чтобы добиться высокой точности управления в разомкнутых системах, необходимо очень тщательно подходить к выбору элементов, образующих передаточную функцию G(s). • Замкнутые системы допускают определенные вариации параметров G(s), поскольку их влияние ослабляется в 1+GH(s ) раз.

Устойчивость линейных систем с обратной связью

Устойчивая система- это динамическая система, обладающая ограниченной реакцией на ограниченный входной сигнал. Устойчивую систему определяют как систему обладающую ограниченной реакцией. Иначе говоря, если система подвергается воздействию ограниченного входного сигнала или возмущения и ее реакция так же является ограниченной по модулю, то такую систему называют устойчивой.

Проиллюстрируем понятие устойчивости на примере конуса находящегося на плоской горизонтальной поверхности: а) Устойчивое положение. б)Нейтрально устойчивое положение. в)Неустойчивое положение.

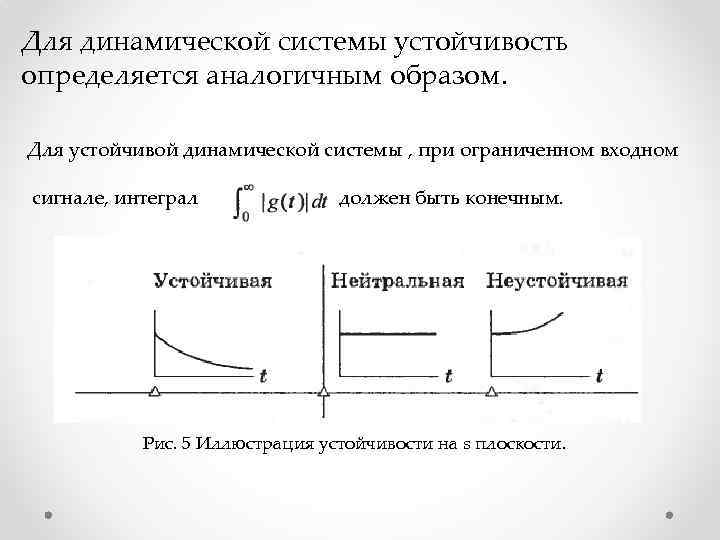Для динамической системы устойчивость определяется аналогичным образом. Для устойчивой динамической системы , при ограниченном входном сигнале, интеграл должен быть конечным. Рис. 5 Иллюстрация устойчивости на s плоскости.

Требования устойчивости для линейных систем: (1. 20) где q(s)=Δ(s)=0 - характеристическое уравнение, корни которого являются полюсами замкнутой системы. Таким образом, чтобы реакция была ограниченной все полюса должны находится в левой половине s плоскости.

Необходимое и достаточное условие того, чтобы замкнутая система была устойчива, состоит в том, чтобы все полюсы передаточной функции системы имели отрицательную действительную часть.

Критерий устойчивости Рауса-Гурвица. Метод Рауса – Гурвица позволяет оценить устойчивость системы, через анализ его характеристического уравнения: : (1. 20) • Для уравнения n-ой степени можно записать: Необходимые условия устойчивости: • Если все корни уравнения (1. 20) расположены в левой полуплоскости s, то все коэффициенты характеристического полинома должны иметь один и тот же знак. • Если система устойчива, то все коэффициенты отличны от нуля. Если условия не выполняются, то система неустойчива, но при выполнении условий, для оценки устойчивости, необходимы дальнейшие исследования.

Критерий Рауса – Гурвица дает необходимое и достаточное условие устойчивости линейных систем. (1. 21) В основе критерия – упорядочение коэффициентов характеристического уравнения (1. 21) в виде таблицы, по следующему правилу: , где = =

Критерий Рауса-Гурвица утверждает, что число корней полинома q(s), с положительной действительной частью равно числу изменений знака в первом столбце таблицы Рауса. Необходимое и достаточное условие: • Для устойчивости системы необходимо и достаточно, чтобы в первом столбце таблицы Рауса не было изменений знака. Частные случаи: 1. В первом столбце нет ни одного нулевого элемента; 2. В первом столбце имеется нулевой элемент, но другие элементы строки, содержащей нуль в первом столбце, отличны от нуля; 3. В первом столбце имеется нулевой элемент, и все остальные элементы соответствующей строки также равны нулю; 4. Случай (3), но характеристический полином имеет кратные корни на мнимой оси;

Пример: Система 2 -ого порядка. Характеристический полином системы второго порядка: Таблица Рауса: , где • Условие устойчивости второго порядка сводится к тому, чтобы все коэффициенты характеристического полинома были положительными или отрицательными.

Пример: Система 3 -ого порядка. Характеристический полином системы третьего порядка: Таблица Рауса: , где

Пример: неустойчивая система. Дан характеристический полином: Таблица Рауса: где Данная система неустойчива при любых значения K. Частный случай 2. Таким образом, критерий Рауса - Гурвица дает частный ответ на вопрос об устойчивости, проверяя, расположены ли какие-либо корни характеристического уравнения в правой половине s-плоскости. Устойчивость системы можно опеределить и по ее моедли в переменных состояния, если система задана свой передаточной функцией.

Анализ устойчивости методом частотных характеристик. Критерий устойчивости Найквиста. • Частотные характеристики системы содержат достаточно информации для определения ее устойчивости. Эти характеристики могут быть получены экспериментальны путем подачи на вход системы синусоидального воздействия и варьирования его частоты; это позволяет исследовать относительную устойчивость системы, при неизвестных значениях параметров. Частотный критерий устойчивости может подсказать, как следует изменить параметры системы, чтобы повысить ее относительную устойчивость. • Частотный критерий устойчивости был предложен Г. Найквистом, и основан на отображении контуров s – плоскости.

Отображение контуров на s – плоскости Контур – это некоторая замкнутая траектория на одной плоскости, отображаемая на другую плоскость соотношением F(s). Поскольку s есть комплексная переменная, s = σ + jω, то функция F(s) также является комплексной; ее можно представить в виде F(s) = u + jυ и изобразить на комплексной F(s) плоскости в координатах u и υ. На F(s) – плоскости мы получаем контур такой же форму, т. е. квадрат, центр которого сдвинут на единицу, а сторона увеличена в 2 раза. Такой тип отображения, при котором на s-плоскости и F(s)-плоскости являются подобными, называется конформным отображением. В качестве примера рассмотрим функцию: (1. 22)

Выражение (1. 22) запишем: Введем: или Рис. 7 Рис. 8

Критерий Найквиста Дана одноконтурная система: Рис. 9 Одноконтурная система управления Для определения устойчивости системы необходимо исследовать ее характеристическое уравнение: (1. 21) L(s) = G(s)+H(s) – рациональная функция переменной s.

• Если P=0, то число корней характеристического уравнения системы равно N Рис. 10 Контур Найквиста на s-плоскости Согласно критерию Найквиста, необходимо подсчитать число охватов начало координат на F(s) – плоскость, используя функцию F’(s): • L(s) – представляется в виде произведения сомножителей (1+L(s) – не обладает таким свойством).

Пример: Система с двумя действительными полюсами Дана одноконтурная система:

Положительная часть мнимой оси отображается в сплошную кривую на рис. 11 б), отрицательная – в пунктирную. • GH(s) – не имеет полюсов в правой полуплоскости – P=0, тогда система устойчива если N=Z=0, т. е. контур на плоскости GH(s)

Таким образом Критерий Найквиста - позволяет по виду амплитуднофазовой частотной характеристики разомкнутой системы оценить устойчивость работы замкнутой системы.

Примеры БТС:

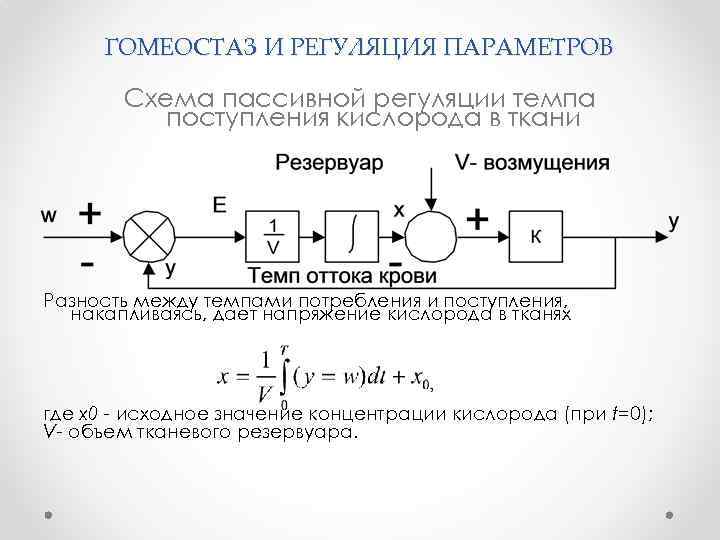ГОМЕОСТАЗ И РЕГУЛЯЦИЯ ПАРАМЕТРОВ Схема пассивной регуляции темпа поступления кислорода в ткани Разность между темпами потребления и поступления, накапливаясь, дает напряжение кислорода в тканях где x 0 - исходное значение концентрации кислорода (при t=0); V- объем тканевого резервуара.

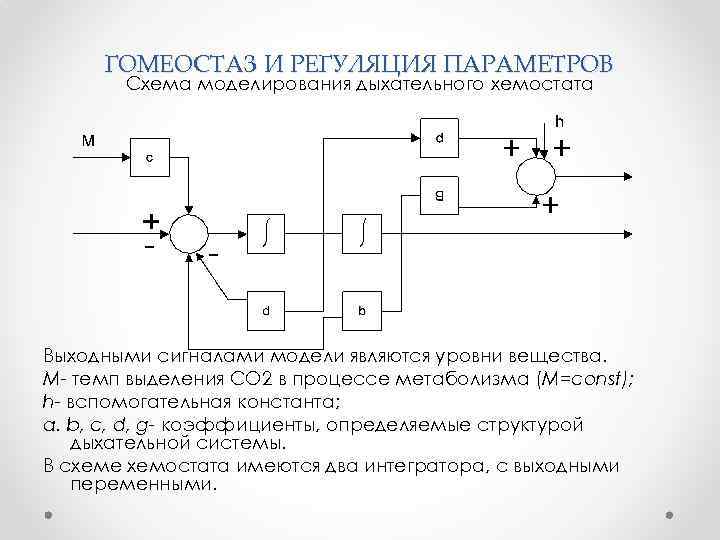ГОМЕОСТАЗ И РЕГУЛЯЦИЯ ПАРАМЕТРОВ Схема моделирования дыхательного хемостата Выходными сигналами модели являются уровни вещества. М- темп выделения CO 2 в процессе метаболизма (M=const); h- вспомогательная константа; а. b, с, d, g- коэффициенты, определяемые структурой дыхательной системы. В схеме хемостата имеются два интегратора, с выходными переменными.

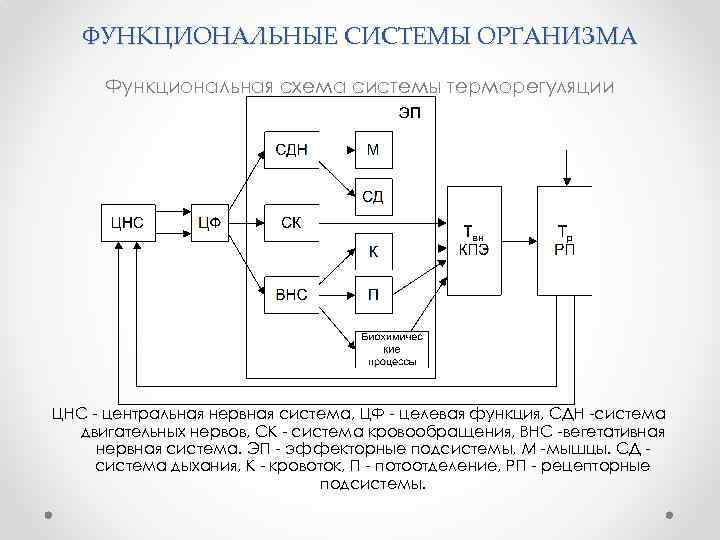ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ ОРГАНИЗМА Функциональная схема системы терморегуляции ЦНС - центральная нервная система, ЦФ - целевая функция, СДН -система двигательных нервов, СК - система кровообращения, ВНС -вегетативная нервная система. ЭП - эффекторные подсистемы, М -мышцы. СД система дыхания, К - кровоток, П - потоотделение, РП - рецепторные подсистемы.