Математические модели 31 01 2018 1

Математические модели 31. 01. 2018 1

• Дифференциальные уравнения физических систем 31. 01. 2018 2

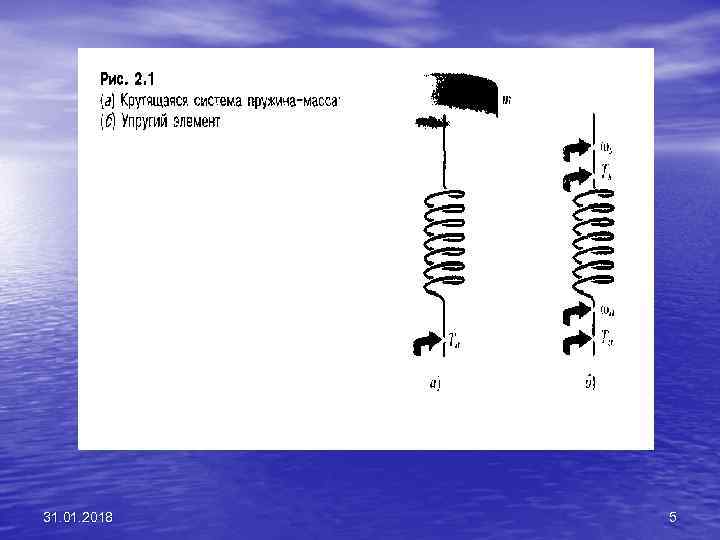
• Рассмотрим крутящуюся систему пружина • масса, изображенную на рис. 2. 1, к которой приложен момент Ta(t). Предположим также, что упругий элемент (пружина) обладает пренебрежимо малой массой по сравнению с диском. Допустим, что нам необходимо изме рить момент. Tx(t), передаваемый массе т. Поскольку согласно допущению пружина не об ладает массой, то сумма действующих на нее моментов должна равняться нулю. т. е. 31. 01. 2018 Ta (t)- Тх (t)=0 3

• откуда имеем Тх (t) = Ta (t). • внешний момент Та(t), приложенный к концу пружины, передается сквозь этот упругий элемент. По этой причине мы будем называть момент сквозной переменной. Аналогичным образом, разность угловых скоростей кон цов упругого элемента равна • ω(t)=ω(x) ω(a) 31. 01. 2018 4

31. 01. 2018 5

• Обозначения: • Сквозные переменные: F—сила, Т—момент, / — ток, Q—объемный расход жидкости, q — тепловой поток. • Относительные переменные: v — • • поступательная скорость, W — угловая скорость, Р — давление, Т— температура. Индуктивные накопители: L — индуктивность, 1/А — обратный коэффициент жесткости. Емкостные накопители: С— емкость, М— масса, J— момент инерции. С, — жидкост ная емкость, С, — тепловая емкость. Расселватс. чи энергии: R — сопротивление, Ь — вязкое трение, R, — тепловое сопротивление. 31. 01. 2018 6

• Для описания механических систем используются законы Ньютона, а для электрических систем — законы Кирхгофа. Например, простой механический амортизатор, изображенный на рис. 2. 2(а), описывается вторым законом Ньютона. 31. 01. 2018 7

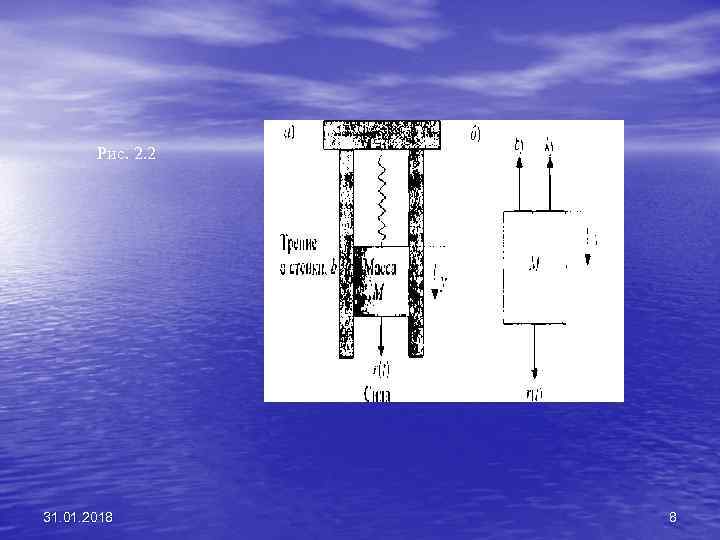Рис. 2. 2 31. 01. 2018 8

• Можно с помощью закона Кирхгофа для токов описать электрическую RLC цепь, представ ленную на рис. 2. 3. В результате мы получим следующее интегро дифференциальное уравнение: 31. 01. 2018 9

31. 01. 2018 10

• Решение дифференциального уравнения, описывающего динамический процесс, может быть получено классическим методом — путем интегрирования с использовани ем неопределенных коэффициентов. Например, если груз сместить в начальное положе ниеy(t) = у(0) и затем отпустить, то движение такой недодемпфированной системы описывается выражением 31. 01. 2018 11

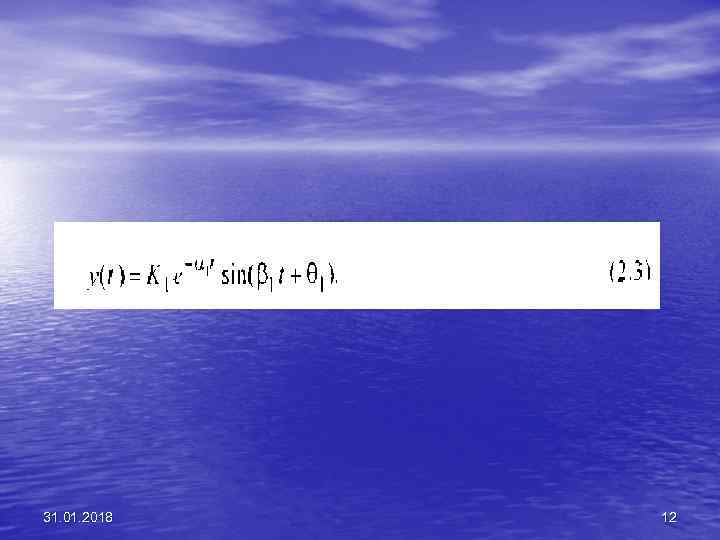31. 01. 2018 12

• Аналогичное решение имеет место для напряжения v(t) RLC-цепи. . если она находит ся под воздействием постоянного тока r(t) =l: 31. 01. 2018 13

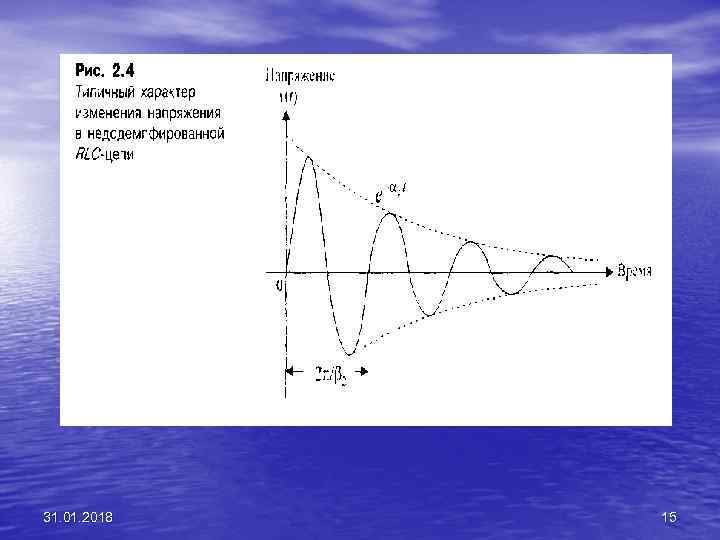
• Типичный характер изменения напряжения в недодемпфированой RLC цепи показан на рис. 2. 4. 31. 01. 2018 14

31. 01. 2018 15

• Чтобы обнаружить более близкое сходство • между дифференциальными уравнениями механических и электрических систем, перепишем уравнение (2. 1) относительно ско рости (2. 2) 31. 01. 2018 16

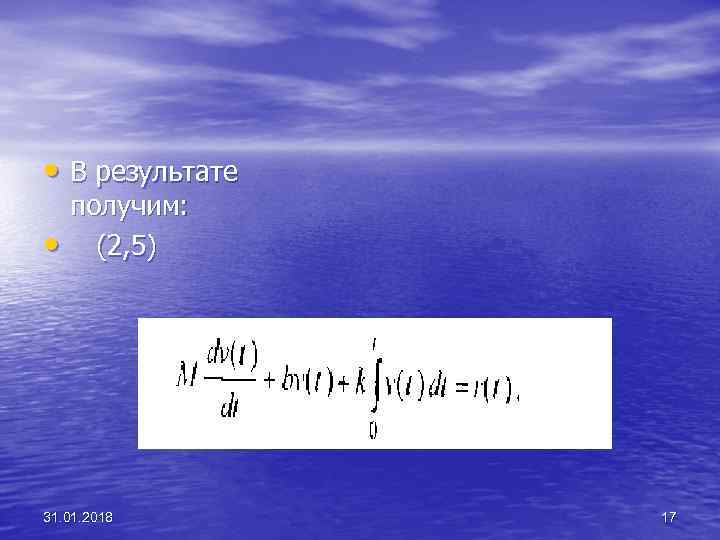• В результате • получим: (2, 5) 31. 01. 2018 17

• Сразу же можно отметить эквивалентность уравнений (2. 5) и (2. 2). только в одном из них переменная v(t) обозначает скорость, а в другом — напряжение. Поэтому данные переменные обычно называют переменными-аналогами, а соответствующие системы — подобными системами. Следовательно, закон изменения скорости будет также иметь вид (2. 4), которому соответствует кривая на рис. 2. 4. 31. 01. 2018 18

• Понятие подобия систем яв ляется очень полезным и эффективным методом при моделировании. Аналогия между напряжением и скоростью, часто называемая аналогией сила ток, вполне естественна, поскольку она характеризует связь между подобными сквозными и относительными пе ременными электрических и механических систем. Однако часто используется и другая аналогия, называемая аналогией сила напряжение, при которой рассматривается подо бие скорости и тока. 31. 01. 2018 19

• Линеаризация физических систем 31. 01. 2018 20

• Линейная система удовлетворяет • свойствам суперпозиции и гомогенности. Если система характеризуется зависимостью y=x 2 то она не является линейной, т. к. для нее не выполняется принцип суперпозиции. Система с уравнением у = mх + b также не является линейной, поскольку она не обладает свойством гомогенности. Однако последнюю систему можно считать линейной в окрестности рабочей точки x 0, y 0, относительно малых прирашений ∆x и ∆y. Если x=x 0+∆x и y=y 0+∆y, то мы получим 31. 01. 2018 21

или 31. 01. 2018 22

• следовательно, ∆у = m∆х. что удовлетворяет необходимым условиям. • Рассмотрим общий случай, когда некоторый элемент характеризуется возмущени ем x(t) и реакцией на него y(t). 31. 01. 2018 23

• Связь между переменными определяется уравнением • у(t) = g[x(t)], (2. 6) • где g[x(t)] показывает, что у(t) является функцией x(t). 31. 01. 2018 24

• Обозначим координату рабочей точ ки через x 0 Непрерывную функцию в окрестности рабочей точки можно разложить в ряд Тейлора: 31. 01. 2018 25

• Касате льная может служить хорошей аппроксимацией исходной кривой в случае малых значений (х -х0), т. е. отклонения от рабочей точки. В таком предположении можно записать: где т есть тангенс угла наклона касательной к кривой в рабочей точке 31. 01. 2018 26

• Окончательно урав нение (2. 8) можно записать (2. 9) 31. 01. 2018 27

31. 01. 2018 28

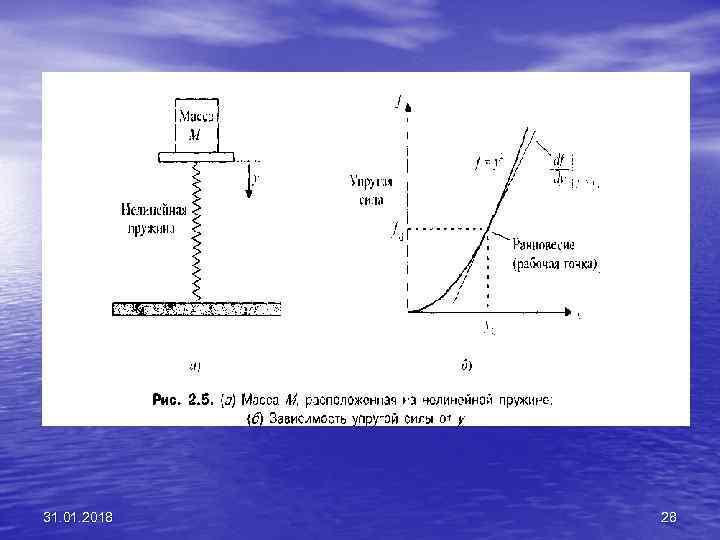
• Рассмотрим случай, когда груз массы М расположен на нелинейной пружине, как по казано на рис. 2. 5(а). Рабочая точка имеет место в положении равновесия, когда упругая сила пружины равна весу груза Mg, где g — ускорение силы тяжести. 31. 01. 2018 29

• Таким образом, f 0= Mg, как показано на рис. 2. 5(6). Для малых отклонений линейная модель описывается уравнением 31. 01. 2018 30

• как показано на рис. 2. 5(6). Следовательно, т = 2 у0. Данную линейную аппроксимацию можно считать точной, поскольку допущение о малости приращений переменных полностью применимо к этой механической системе. 31. 01. 2018 31

• К нелинейной функции нескольких переменных также можно применить разложение в ряд Тейлора в окрестности рабочей точки. Пренебрегая членами высшего порядка малости, линейную аппроксимацию можно представить в виде: 31. 01. 2018 32

где х0 — рабочая точка. Ниже приводится пример, иллюстрирующий применение метода линеаризации. 31. 01. 2018 33

• Преобразование Лапласа 31. 01. 2018 34

• Определение реакции системы на входное воздействие подразумевает следующие действия: • 1. Получение дифференциальных уравнений. • 2. Преобразование по Лапласу этих дифференциальных уравнений. • 3. Решение полученных алгебраических уравнений относительно переменной, пред ставляющей интерес. 31. 01. 2018 35

• Для того чтобы функция имела преобразование Лапласа, достаточно, чтобы вы полнялось условие 31. 01. 2018 36

данный интеграл должен сходиться для некоторого действительного положительного σ0. Если | f'(t) | < M'еat для всех положительных t. то интеграл будет сходиться при σ1 > а. Таким образом, область сходимости определяется неравенством ∞ > σ1 > а, где σ1 известна как абсцисса абсолютной сходимости. Все физически реализуемые сигналы имеют преоб 31. 01. 2018 37

31. 01. 2018 38

• Обратное преобразование Лапласа обычно находят путем разложения. F(s) на простые дроби с помощью правила Хевисайда. Этот метод, в частности, полезен при анализе и синтезе систем управления, т. к. он позволяет легко выявить влияние каждого корня характеристического уравнения системы. 31. 01. 2018 39

• Чтобы проиллюстрировать преимущества преобразования Лапласа, рассмотрим еше раз механическую колебательную систему, описываемую уравнением (2. 1), которое имеет вид 31. 01. 2018 40

• Нам необходимо получить решение этого уравнения, т. е. выражениеy(t) 31. 01. 2018 41

• Преобразование Лапласа и использование s плоскости являются очень ценными методами анализа и синтеза систем, когда акцент делается на определение переходных режимов и точность в установившемся состоянии 31. 01. 2018 42