Математические методы в психологии Математическая статистика введение

Математические методы в психологии. Математическая статистика. введение

Курс «математические методы в психологии» Компетенции: Умение подбирать метод анализа данных под задачу: Умение правильно определять уровень измерения переменных Знать основные понятия, принципы математической статистики Умение адекватно использовать формулы, проводить расчеты и делать выводы

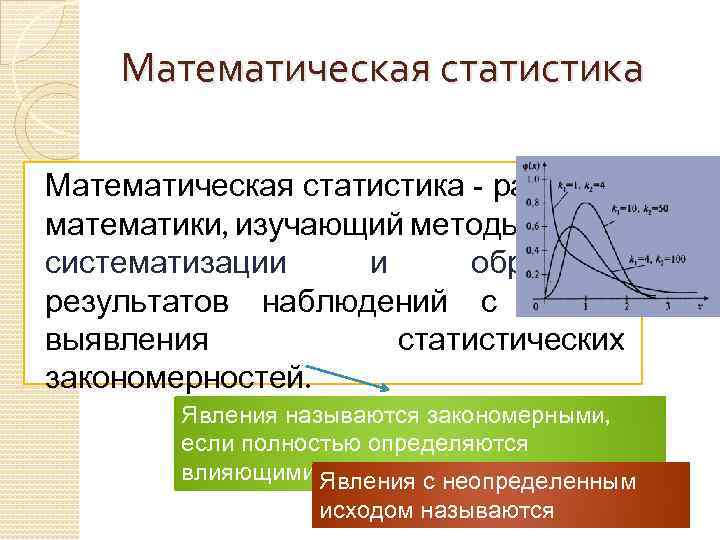Математическая статистика - раздел математики, изучающий методы сбора, систематизации и обработки результатов наблюдений с целью выявления статистических закономерностей. Явления называются закономерными, Знание законовявления составляют Закономерные позволяет предсказать если полностью определяются явления объект научных исследований главный не производя реальных опытов влияющими Явления с неопределенным на них факторами исходом называются

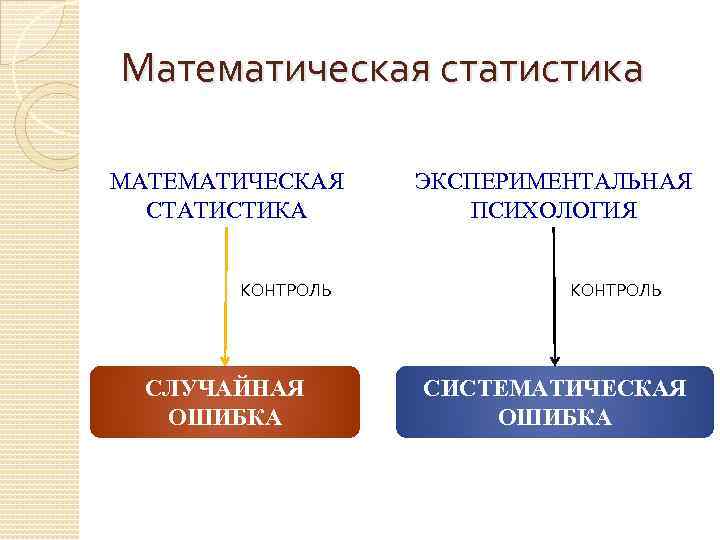Математическая статистика МАТЕМАТИЧЕСКАЯ СТАТИСТИКА КОНТРОЛЬ СЛУЧАЙНАЯ ОШИБКА ЭКСПЕРИМЕНТАЛЬНАЯ ПСИХОЛОГИЯ КОНТРОЛЬ СИСТЕМАТИЧЕСКАЯ ОШИБКА

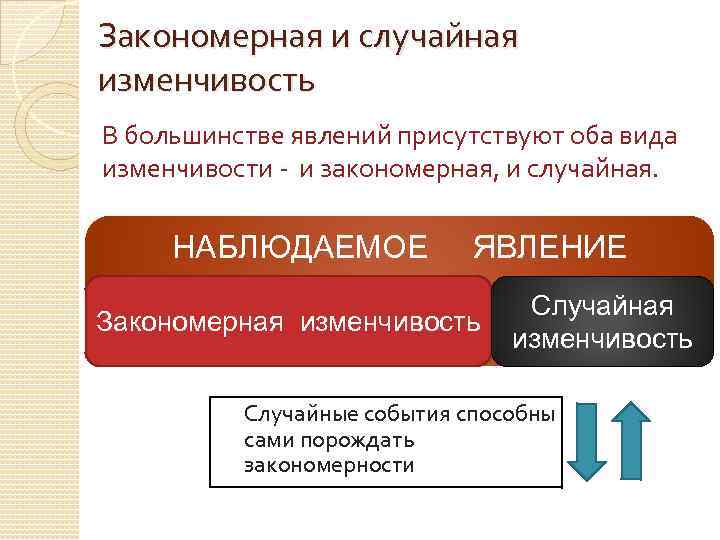Закономерная и случайная изменчивость В большинстве явлений присутствуют оба вида изменчивости - и закономерная, и случайная. НАБЛЮДАЕМОЕ ЯВЛЕНИЕ Закономерная изменчивость Случайные события способны сами порождать закономерности

Закономерная и случайная изменчивость щелчок

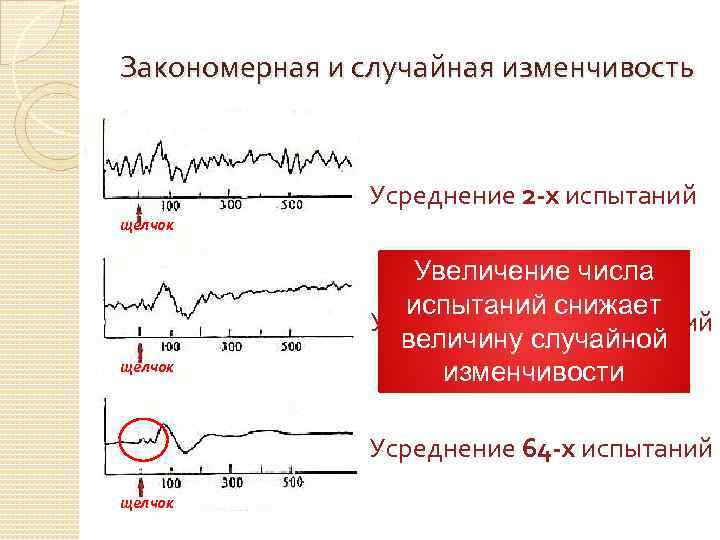Закономерная и случайная изменчивость Усреднение 2 -х испытаний щелчок Увеличение числа испытаний снижает Усреднение 16 -и испытаний величину случайной изменчивости Усреднение 64 -х испытаний щелчок

Вероятность события v Каждому событию, возможному в данном испытании, может быть 0 ≤ P(A) ≤ 1 приписанная числовая мера его правдоподобия, называемая его вероятностью v Событие называется достоверным, достоверным если в результате испытания оно P(A) = 1 обязательно должно произойти (или с большой долей вероятностью) v Событие называется невозможным, если в результате испытания оно P(A) = 0 вообще не может произойти

Вероятность альфа Вероятность α - альфа уровень - уровень значимости - ошибка 1 -го рода вероятность случайной изменчивости α < 0, 05 (p < 0, 05) α < 0, 01 (p < 0, 01)

Вероятность альфа

Случайная величина Случайной величиной (переменной) называется признак (свойство), который принимает различные значения в результате наблюдения значения переменной = варианты = реализации

Случайная величина Результаты по тестам (в баллах) Время решения задач и другие … Социометрически й индекс Дистанция, угол поворота тела и наклонов кол-во взглядов

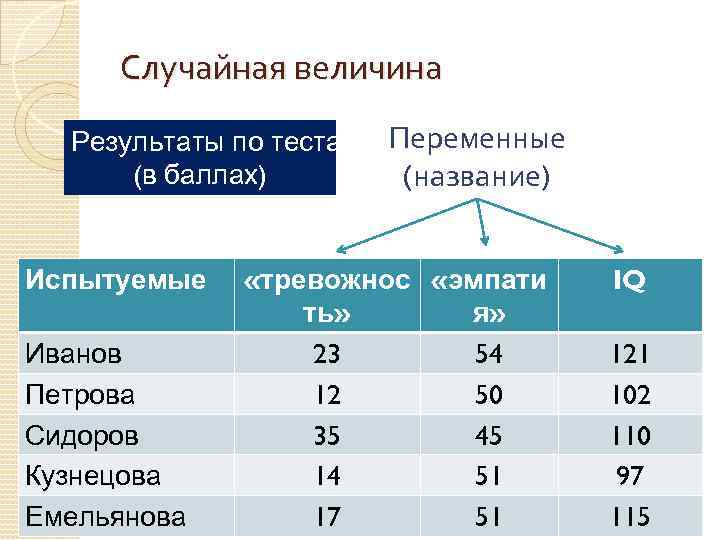Случайная величина Результаты по тестам Переменные (в баллах) (название) Испытуемые Иванов Петрова Сидоров Кузнецова Емельянова «тревожнос «эмпати ть» я» 23 54 12 50 35 45 14 51 17 51 IQ 121 102 110 97 115

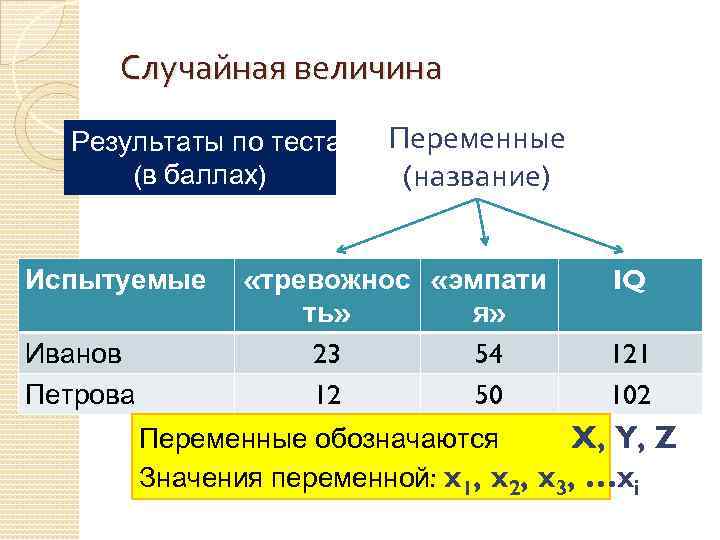Случайная величина Результаты по тестам Переменные (в баллах) (название) Испытуемые Иванов Петрова «тревожнос «эмпати ть» я» 23 54 12 50 IQ 121 102 Переменные обозначаются X, Y, Z Значения переменной: x 1, x 2, x 3, …xi

Регистрация переменной Явление, феномен, свойство Измерительный инструмент

Непрерывные и дискретные величины Непрерывная случайная величина Принимает ВСЕ значения из некоторого конечного или бесконечного промежутка. Множество значений бесконечно и несчетно. Дискретная случайная величина Принимает отдельные, изолированные значения. Множество значений конечно или, если бесконечно, то счетное.

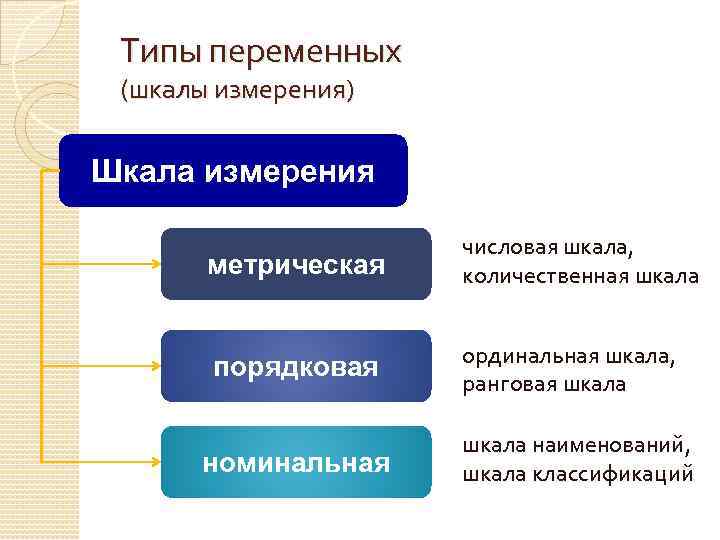Типы переменных (шкалы измерения) Шкала измерения метрическая числовая шкала, количественная шкала порядковая ординальная шкала, ранговая шкала номинальная шкала наименований, шкала классификаций

Номинальная шкала (шкала наименований, шкала классификаций) v. Используется только для классификации индивидуумов в популяции v. Каждому значению присваивается свое обозначение так , чтобы обозначения разных классов не совпадали v. Для шкалы наименований не имеет смысла арифметические операции, кроме операции идентификации = и ≠

Номинальная шкала ПОЛ ПРОФЕССИЯ РУКОСТЬ НАЦИОНАЛЬНОСТЬ

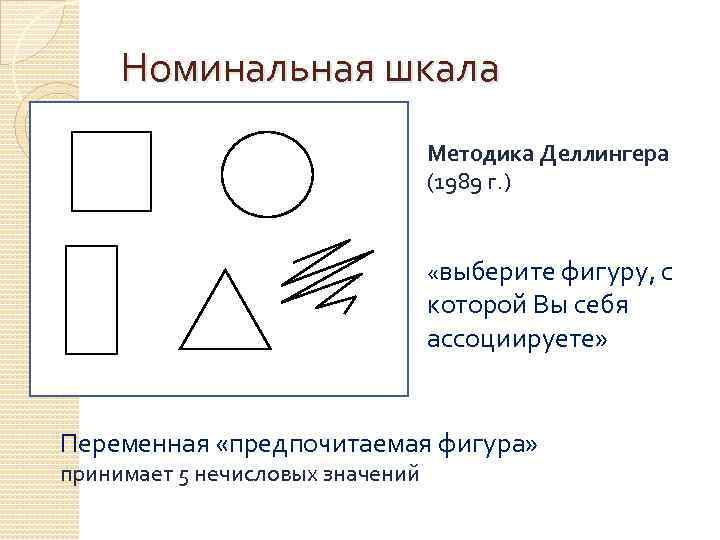Номинальная шкала Методика Деллингера (1989 г. ) «выберите фигуру, с которой Вы себя ассоциируете» Переменная «предпочитаемая фигура» принимает 5 нечисловых значений

Номинальная шкала Методика «предпочитаемое животное» (Пигем, 1945 г. ) 1. «кем бы ты хотел быть, если бы не мог быть человеком? » (и почему? ) 2. «кем бы ты больше всего не хотел быть? » (и почему? ) Переменная «ведущая мотивация» : принимает 4 нечисловых значения эстетика агрессия автономия помощь

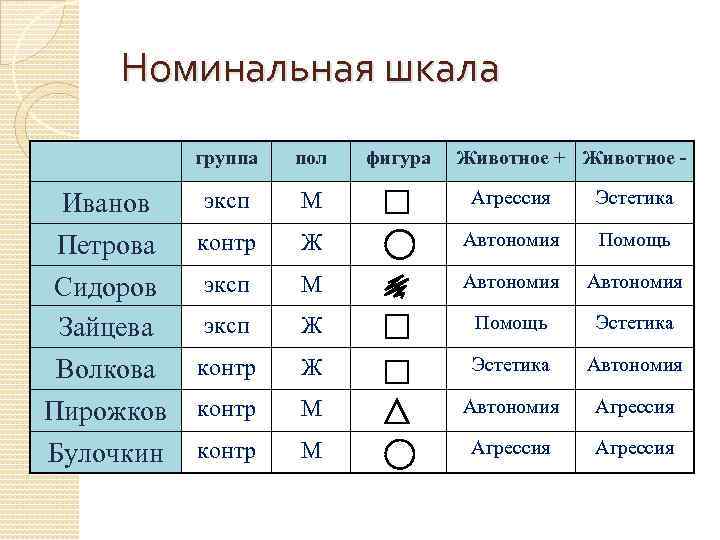Номинальная шкала группа Иванов Петрова Сидоров Зайцева Волкова Пирожков Булочкин пол фигура Животное + Животное - эксп М Агрессия Эстетика контр Ж Автономия Помощь эксп М Автономия эксп Ж Помощь Эстетика контр Ж Эстетика Автономия контр М Автономия Агрессия контр М Агрессия

Порядковая шкала (ранговая, ординальная) v Не только разбивает на группы, но и упорядочивает их v Количество вариантов должно быть больше двух v Каждому классу присваивается значение так, чтобы порядок обозначений соответствовал порядку классов (используется только упорядоченная система обозначений 1 2 … n, А Б В … Я) v Кроме операции идентификации в этой шкале возможно сравнение < и > v В этой шкале при сравнении объектов невозможно сказать насколько один объект больше другого

Порядковая шкала 1 место (ранговая, ординальная) 23

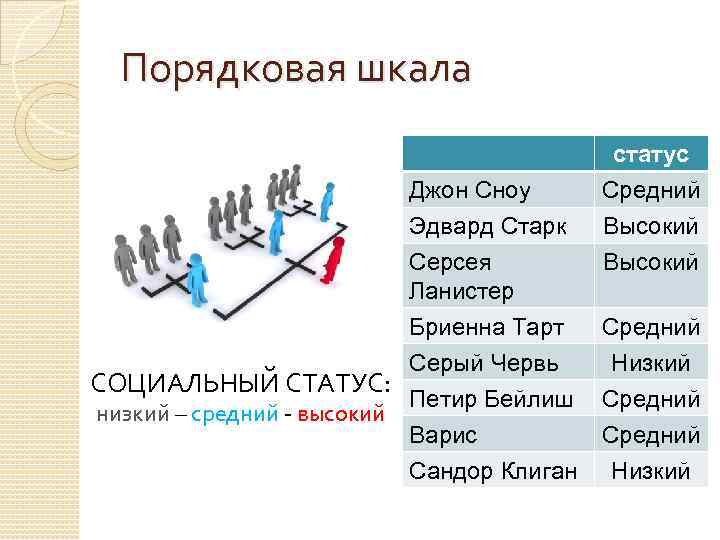Порядковая шкала Джон Сноу Эдвард Старк Серсея Ланистер Бриенна Тарт Серый Червь СОЦИАЛЬНЫЙ СТАТУС: Петир Бейлиш низкий – средний - высокий Варис Сандор Клиган статус Средний Высокий Средний Низкий

Порядковая шкала ОЦЕНКА ЗА ЗНАНИЯ: 2– 3– 4 -5 Оценка по матметодам оценк а оценка Джон Сноу 4 Хорошо Эдвард Старк 4 Хорошо Серсея Ланистер 3 Удовлетворительн о Тирион Ланнистер 5 отлично

Порядковая шкала Измерительный инструмент Стратегия выставления оценок преподавателем Строгий преподаватель пятерки выставляет только в исключительных случаях 5 4 реальный уровень знаний Либеральный преподаватель двойки выставляет только в исключительных случаях 5 4 3 3

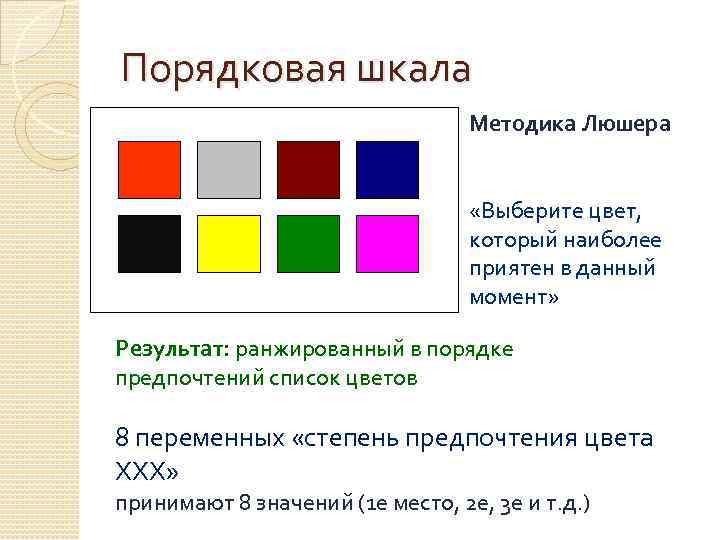Порядковая шкала Методика Люшера «Выберите цвет, который наиболее приятен в данный момент» Результат: ранжированный в порядке предпочтений список цветов 8 переменных «степень предпочтения цвета ХХХ» принимают 8 значений (1 е место, 2 е, 3 е и т. д. )

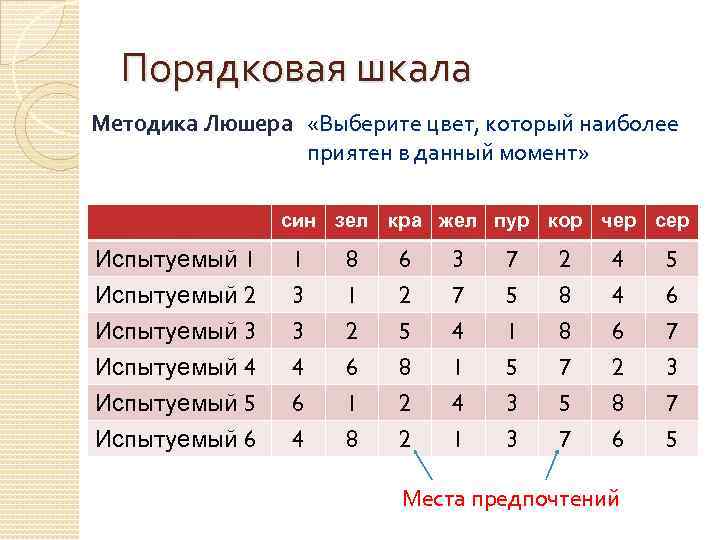Порядковая шкала Методика Люшера «Выберите цвет, который наиболее приятен в данный момент» син зел кра жел пур кор чер сер Испытуемый 1 Испытуемый 2 Испытуемый 3 1 3 3 8 1 2 6 2 5 3 7 4 7 5 1 2 8 8 4 4 6 5 6 7 Испытуемый 4 Испытуемый 5 Испытуемый 6 4 6 1 8 8 2 2 1 4 1 5 3 3 7 5 7 2 8 6 3 7 5 Места предпочтений

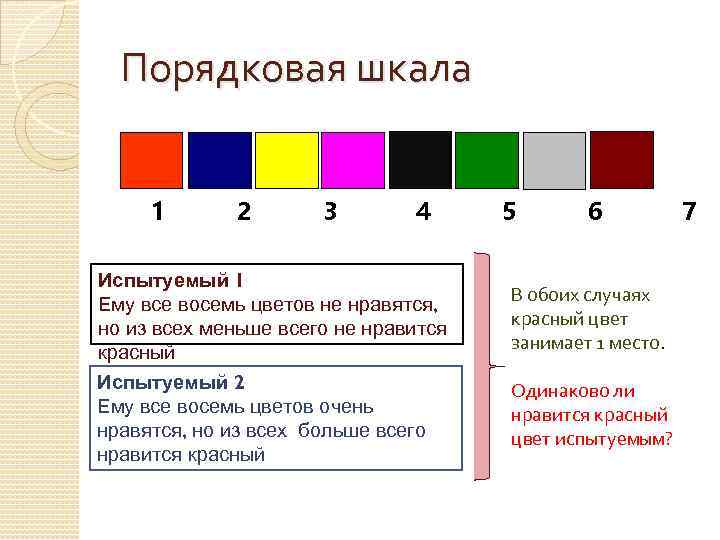Порядковая шкала 1 2 3 4 Испытуемый 1 Ему все восемь цветов не нравятся, но из всех меньше всего не нравится красный Испытуемый 2 Ему все восемь цветов очень нравятся, но из всех больше всего нравится красный 5 6 В обоих случаях красный цвет занимает 1 место. Одинаково ли нравится красный цвет испытуемым? 7

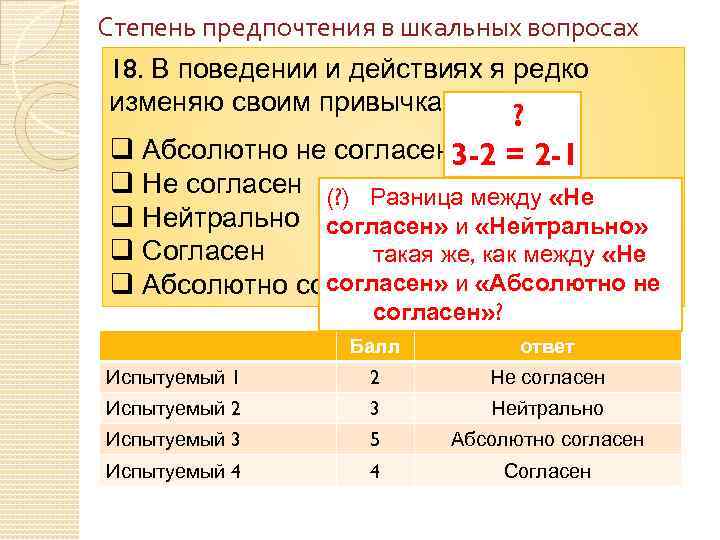Степень предпочтения в шкальных вопросах 18. В поведении и действиях я редко изменяю своим привычкам ? q Абсолютно не согласен 3 -2 = 2 -1 q Не согласен (? ) Разница между «Не q Нейтрально согласен» и «Нейтрально» q Согласен такая же, как между «Не согласен» q Абсолютно согласен и «Абсолютно не согласен» ? Балл ответ Испытуемый 1 2 Не согласен Испытуемый 2 3 Нейтрально Испытуемый 3 5 Абсолютно согласен Испытуемый 4 4 Согласен

Порядковая шкала Методика Рокича «упорядочите ценности по степени важности от 1 до 18» 18 переменных «значимость ценности ХХХ» принимают 18 значений (1 е место, 2 е, 3 е и т. д. )

Метрическая шкала (числовая, количественная) v Имеет единицу измерения (равные интервалы) v Позволяет количественно оценить различия между объектами, группами v Доступны арифметические Шкала интервалов на сколько раз относительный ноль операции: сложение (вычитание) и, Шкала в некоторых случаях, умножение отношений (деление) во сколько раз абсолютный ноль

Метрическая шкала ДИСТАНЦИЯ между участниками коммуникации ОБЪЕМ ГРУППЫ

Метрическая шкала ВРЕМЯ РЕШЕНИЯ ЗАДАЧ УГОЛ поворота головы

Метрическая или порядковая шкала? Проблема составных баллов в опросниках Каждый вопрос – это отдельное измерение Балл по тесту получается как сумма баллов по отдельным вопросам Проблема: вопросы не являются идентичными с точки зрения вклада в суммарное измерение (разные веса, неравные интервалы)

Метрическая или порядковая шкала? Проблема составных баллов в опросниках ВЕС: 0, 375 0, 458 0, 765 0, 564 0, 811 0, 347 1 2 3 4 5

Неравные интервалы Рост = 5 прутиков

Метрическая или порядковая шкала? Проблема составных баллов в опросниках Испытуемый 1 Выбрал три ключевых ответа: 3, 4 и 5 В сумме получил 3 балла 4 3 Испытуемый 2 Выбрал три ключевых ответа: 1, 2 и 4 В сумме получил 3 балла 1 2 4 5

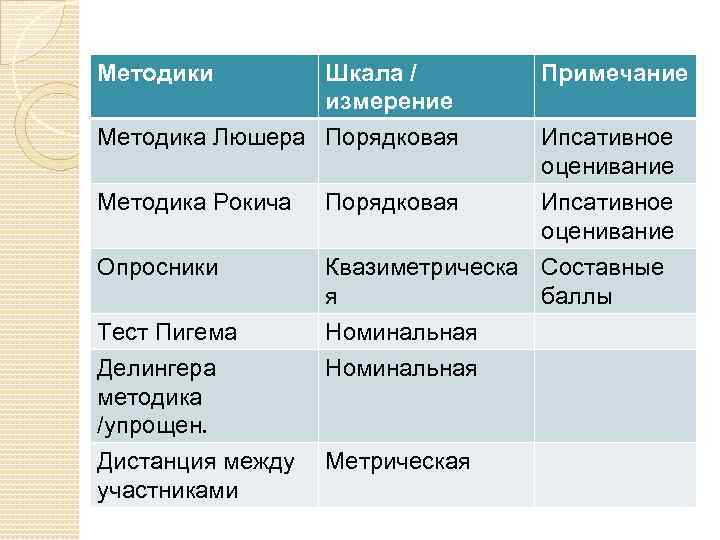Методики Шкала / измерение Примечание Методика Люшера Порядковая Ипсативное оценивание Методика Рокича Порядковая Ипсативное оценивание Опросники Квазиметрическа Составные я баллы Тест Пигема Делингера методика /упрощен. Номинальная Дистанция между участниками Метрическая

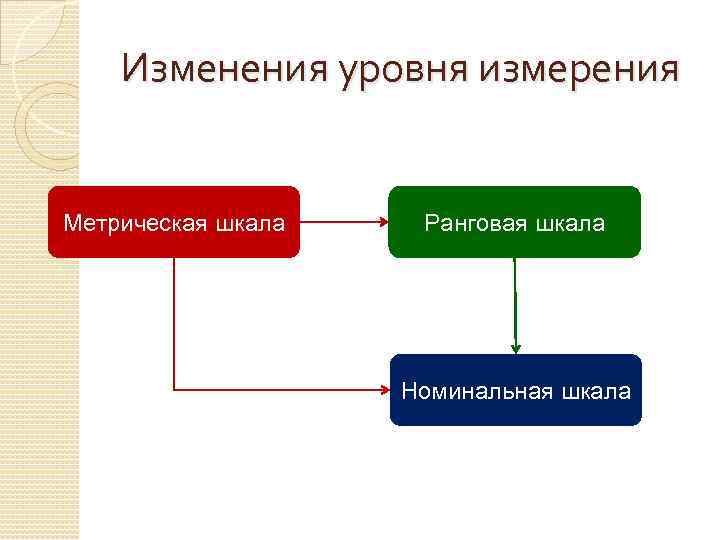Изменения уровня измерения Метрическая шкала Ранговая шкала Номинальная шкала

Задание: у 50 школьников выпускных классов исследовался уровень интеллекта по методу Стенфорд-Бине. Был получен следующий ряд IQ: 119 86 100 93 108 88 85 114 99 118 92 115 112 117 82 100 86 129 103 96 90 118 101 104 88 113 89 104 127 103 112 90 121 96 88 108 70 113 90 116 111 96 99 123 103 83 97 87 101 91 неупорядоченный ряд данных

Задание: у 50 школьников выпускных классов исследовался уровень интеллекта по методу Стенфорд-Бине. Был получен следующий ряд IQ: 70 1 89 82 83 85 86 86 87 88 88 88 90 90 90 91 92 93 96 96 96 97 99 99 100 101 103 103 104 108 111 112 113 114 115 116 117 118 119 121 123 127 129 упорядоченный ряд значений

Задание: у 50 школьников выпускных классов исследовался уровень интеллекта по методу Стенфорд-Бине. Был получен следующий ряд IQ: 70 1 89 82 2 90 83 85 86 86 87 88 88 88 90 90 91 92 93 96 96 96 97 99 99 100 101 103 103 104 108 111 112 113 114 115 116 117 118 119 121 123 127 129 упорядоченный ряд значений

Задание: у 50 школьников выпускных классов исследовался уровень интеллекта по методу Стенфорд-Бине. Был получен следующий ряд IQ: 70 1 89 82 2 90 83 3 90 85 4 90 86 86 87 88 88 88 91 92 93 96 96 96 97 99 99 100 101 103 103 104 108 111 112 113 114 115 116 117 118 119 121 123 127 129 упорядоченный ряд значений

Задание: у 50 школьников выпускных классов исследовался уровень интеллекта по методу Стенфорд-Бине. Был получен следующий ряд IQ: 70 1 89 82 2 90 83 3 90 85 4 90 86 5 91 86 6 92 87 88 88 88 93 96 96 96 97 99 99 100 101 103 103 104 108 111 112 113 114 115 116 117 118 119 121 123 127 129 упорядоченный ряд значений

Задание: у 50 школьников выпускных классов исследовался уровень интеллекта по методу Стенфорд-Бине. Был получен следующий ряд IQ: 70 1 89 82 2 90 83 3 90 85 4 90 86 5, 5 91 86 5, 5 92 8 7 93 88 88 88 96 96 96 97 99 99 100 101 103 103 104 108 111 112 113 114 115 116 117 118 119 121 123 127 129 упорядоченный ряд значений

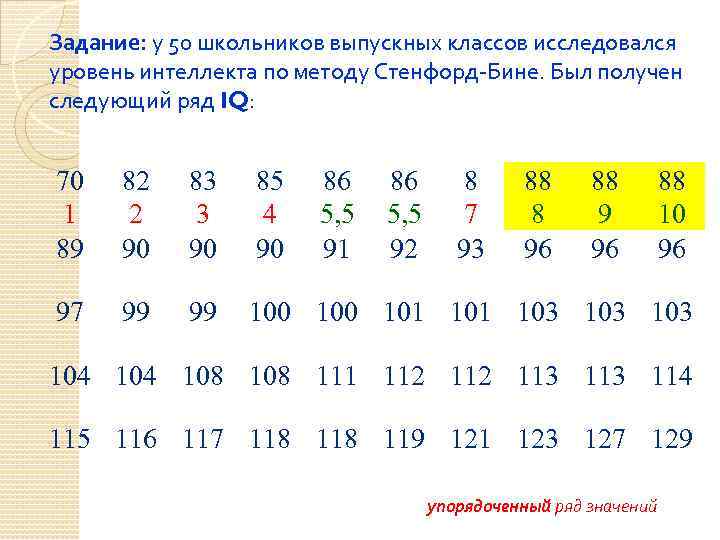Задание: у 50 школьников выпускных классов исследовался уровень интеллекта по методу Стенфорд-Бине. Был получен следующий ряд IQ: 70 1 89 82 2 90 83 3 90 85 4 90 86 5, 5 91 86 5, 5 92 8 7 93 88 8 96 88 9 96 88 10 96 97 99 99 100 101 103 103 104 108 111 112 113 114 115 116 117 118 119 121 123 127 129 упорядоченный ряд значений

Задание: у 50 школьников выпускных классов исследовался уровень интеллекта по методу Стенфорд-Бине. Был получен следующий ряд IQ: 70 1 89 82 2 90 83 3 90 85 4 90 86 5, 5 91 86 5, 5 92 8 7 93 88 9 96 97 99 99 100 101 103 103 104 108 111 112 113 114 115 116 117 118 119 121 123 127 129 упорядоченный ряд значений

Задание: у 50 школьников выпускных классов исследовался уровень интеллекта по методу Стенфорд-Бине. Был получен следующий ряд IQ: 70 1 89 11 97 21 104 31, 5 115 41 82 2 90 13 99 22, 5 104 31, 5 116 42 83 3 90 13 99 22, 5 108 33, 5 117 43 85 4 90 13 100 24, 5 108 33, 5 118 44, 5 86 5, 5 91 15 100 24, 5 111 35 118 44, 5 86 5, 5 92 16 101 26, 5 112 36, 5 119 46 8 7 93 17 101 26, 5 112 36, 5 121 47 88 9 96 19 103 29 113 38, 5 123 48 88 88 9 9 96 96 19 19 103 29 29 113 114 38, 5 40 127 129 49 50

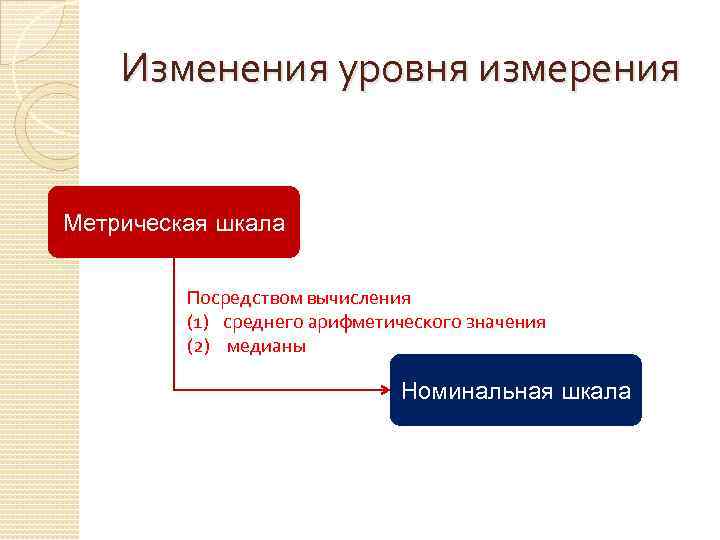Изменения уровня измерения Метрическая шкала Посредством вычисления (1) среднего арифметического значения (2) медианы Номинальная шкала

Задание: у 50 школьников выпускных классов исследовался уровень интеллекта по методу Стенфорд-Бине. Был получен следующий ряд IQ: 70 82 83 85 86 86 87 88 88 88 н н н н н 89 90 90 90 91 92 93 96 96 96 н н н н н 97 99 99 100 101 103 103 н н н в в в 104 108 111 112 113 114 в в в в в 115 116 117 118 119 121 123 127 129 в в в в в упорядоченный ряд значений

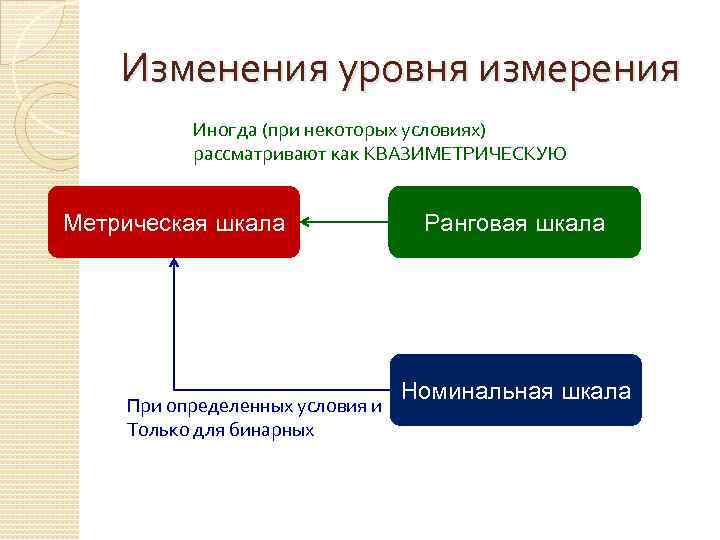Изменения уровня измерения Иногда (при некоторых условиях) рассматривают как КВАЗИМЕТРИЧЕСКУЮ Метрическая шкала При определенных условия и Только для бинарных Ранговая шкала Номинальная шкала

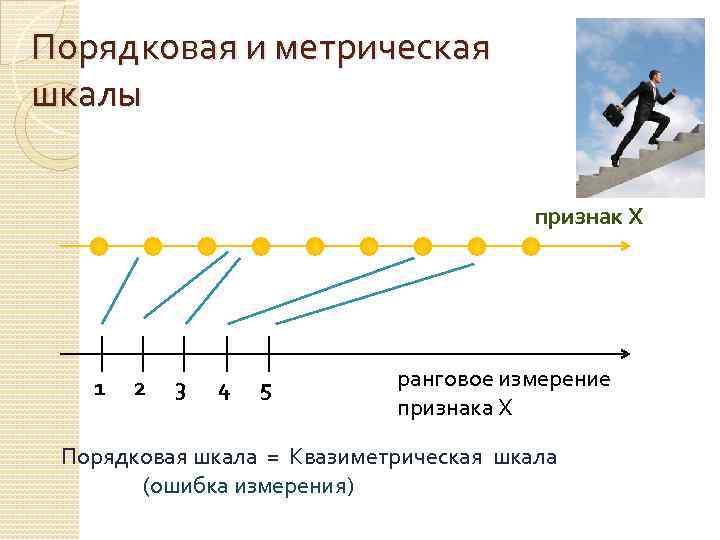Порядковая и метрическая шкалы признак Х 1 2 3 4 5 ранговое измерение признака Х Порядковая шкала = Квазиметрическая шкала (ошибка измерения)