Математические методы в экологии Основы теории вероятностей

Математические методы в экологии Основы теории вероятностей + Математическая статистика + Прикладная статистика

Математическая статистика: Задачи 1. 1. Задачи математической статистики Математическая статистика – наука о математических методах, позволяющим по статистическим данным (например, по реализациям случайной величины) построить теоретико-вероятностную модель исследуемого явления. Задачи математической статистики в определенном смысле являются обратными к задам теории вероятностей. Типичная задача ТВ: по известным вероятностям простых случайных событий вычислить вероятность более сложного события. Пример. Ловля рыбы на удочку. Вероятность выловить окуня p = 0. 2. Какова вероятность события «среди 20 пойманных рыб 5 окуней» ? Типичная задача МС: на основании результатов наблюдений оценить вероятность случайного события или характеристики случайной величины. Пример. Среди 20 пойманных рыб оказалось 5 окуней. Что можно сказать о вероятности поймать окуня и насколько этой оценке можно доверять?

Математическая статистика: Задачи Основные задачи математической статистики: 1. Предварительная обработка данных. Упорядочение результатов эксперимента, представление их в удобном виде. Как представить огромный массив наблюдений, какие числовые характеристики использовать? 2. Оценка неизвестной величины: вероятности события, функции распределения случайной величины, параметров распределения. Каково среднее значение признака в той или иной выборке, насколько точна оценка? 3. Проверка статистических гипотез. Отличаются ли показатели опытной и контрольной группы? Достоверно ли действие изучаемого фактора? 4. Установление формы и степени связи между случайными величинами.

Математическая статистика: Выборочный метод 1. 2. Основы выборочного метода Генеральной совокупностью называется изучаемое множество объектов. Примеры: - население Нижнего Новгорода; - березы заповедника Керженский; - листья конкретной березы; - лейкоциты крови особи (человека, лягушки…) Выборочной совокупностью или выборкой называют совокупность случайно отобранных для исследования объектов. Примеры: - пациенты 14 -й поликлиники; - совокупность деревьев, обследованных на пробных площадках в ходе полевого сезона; - набор собранных листьев; - совокупность лейкоцитов конкретного мазка крови Число элементов выборки называется ее объемом.

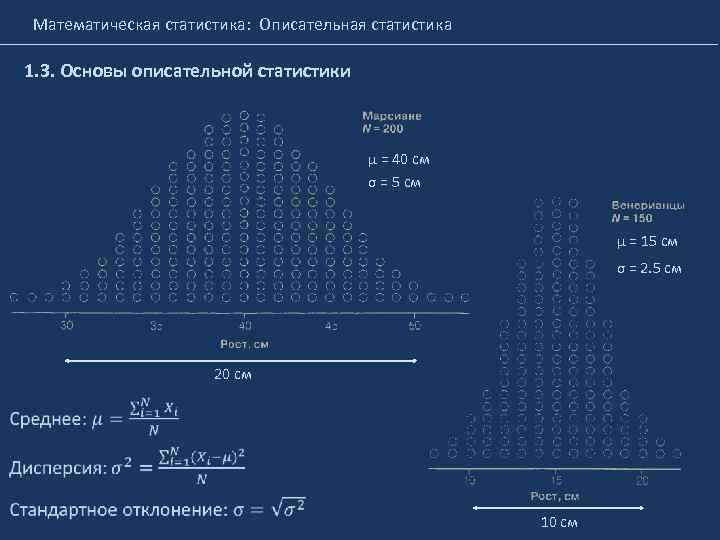Математическая статистика: Описательная статистика 1. 3. Основы описательной статистики μ = 40 см σ = 5 см μ = 15 см σ = 2. 5 см 20 см 10 см

Математическая статистика: Описательная статистика

Математическая статистика: Описательная статистика Медиана – значение, разделяющее совокупность пополам.

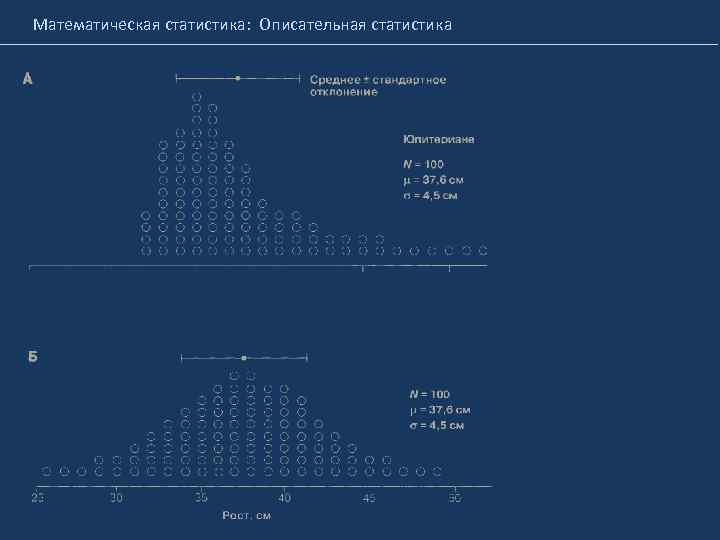
Математическая статистика: Описательная статистика Q-й процентиль – значение, меньше которого Q % совокупности. P (X < X(Q)) = Q/100

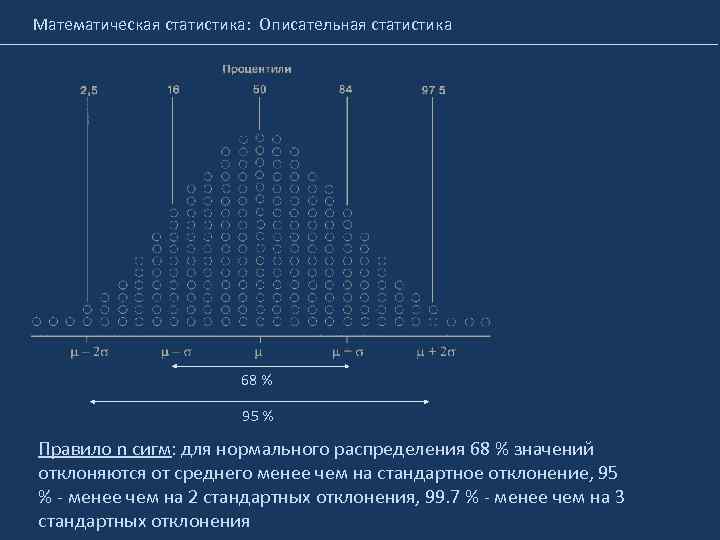Математическая статистика: Описательная статистика 68 % 95 % Правило n сигм: для нормального распределения 68 % значений отклоняются от среднего менее чем на стандартное отклонение, 95 % - менее чем на 2 стандартных отклонения, 99. 7 % - менее чем на 3 стандартных отклонения

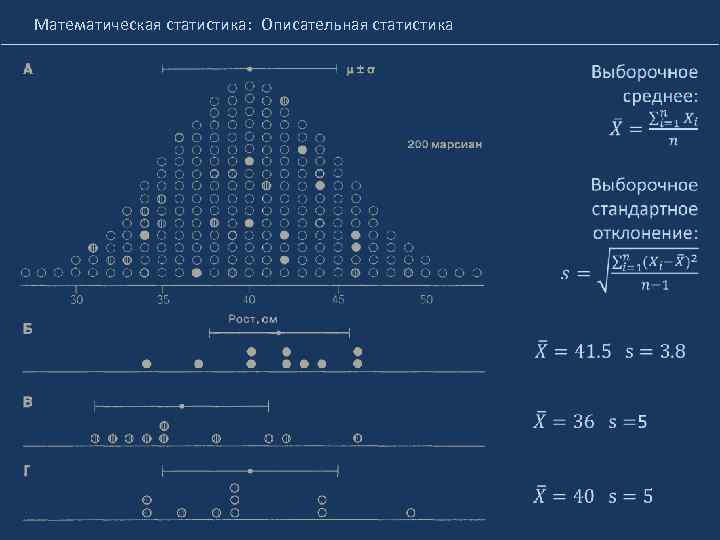Математическая статистика: Описательная статистика

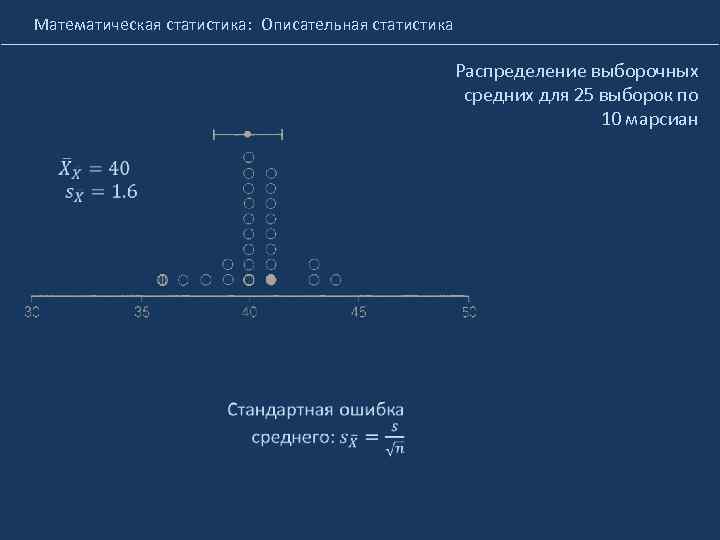Математическая статистика: Описательная статистика Распределение выборочных средних для 25 выборок по 10 марсиан

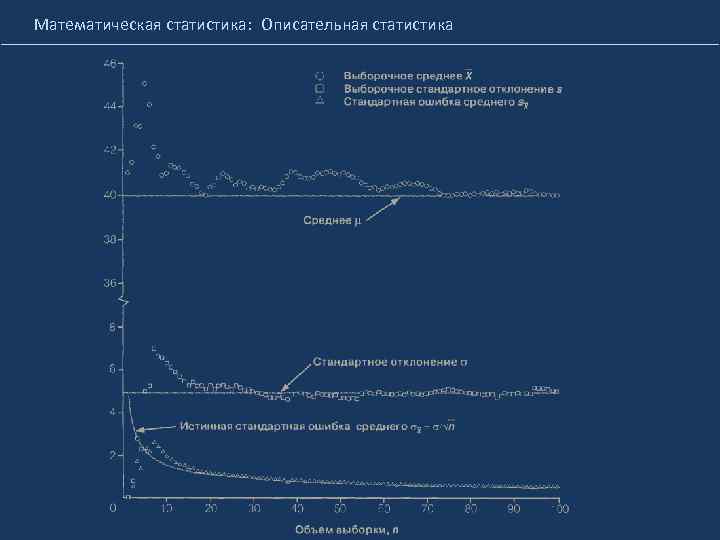Математическая статистика: Описательная статистика

Математическая статистика: t-критерий Стьюдента 1. 4. Сравнение двух групп: t-критерий Стьюдента Испытание диуретика Насколько можно быть уверенным в действии фактора (препарата)? Достоверно ли отличие между средними значениями? Нуль-гипотеза H 0: отличия между выборками обусловлены случайностью, или обе группы являются выборками из одного и того же распределения Альтернативная гипотеза H 1: отличия между выборками обусловлены действием препарата, выборки происходят из разных распределений с различающимися средними

Математическая статистика: t-критерий Стьюдента Суть метода: определить вероятность получить наблюдаемые отличия при условии справедливости нуль-гипотезы

Математическая статистика: t-критерий Стьюдента

Математическая статистика: t-критерий Стьюдента Чем больше |t|, тем менее вероятно получить такое значение при условии справедливости нуль-гипотезы. Значение критерия, начиная с которого мы отвергаем нулевую гипотезу, называется критическим значением. Вероятность ошибочно отвергнуть верную нулевую гипотезу, то есть найти различия там, где их нет, обозначается Р. Как правило, считают достаточным, чтобы эта вероятность не превышала 5%. Максимальная приемлемая вероятность ошибочно отвергнуть нулевую гипотезу называется уровнем значимости и обозначается α.

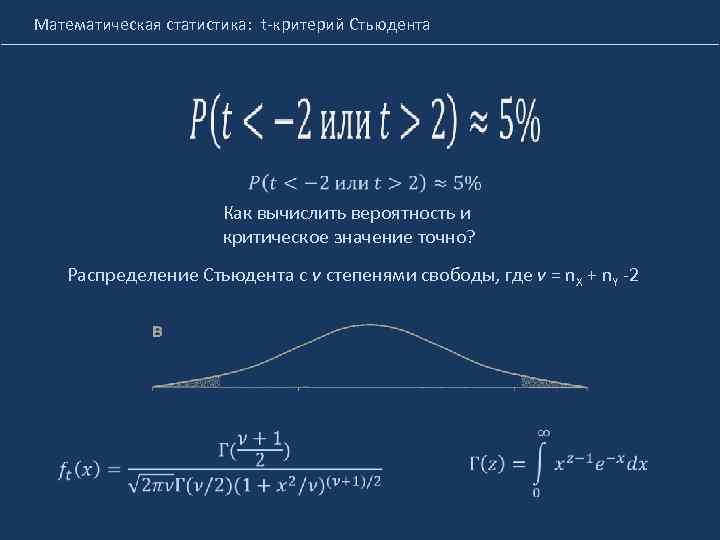Математическая статистика: t-критерий Стьюдента Как вычислить вероятность и критическое значение точно? Распределение Стьюдента с ν степенями свободы, где ν = n. X + n. Y -2

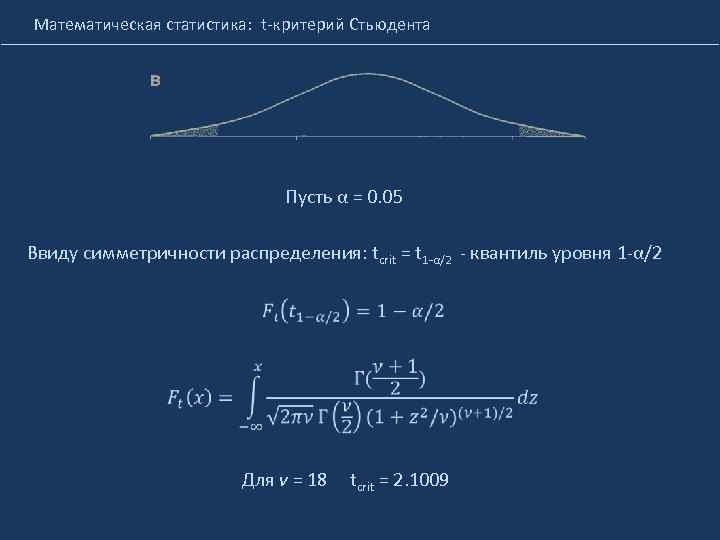Математическая статистика: t-критерий Стьюдента Пусть α = 0. 05 Ввиду симметричности распределения: tcrit = t 1 -α/2 - квантиль уровня 1 -α/2 Для ν = 18 tcrit = 2. 1009

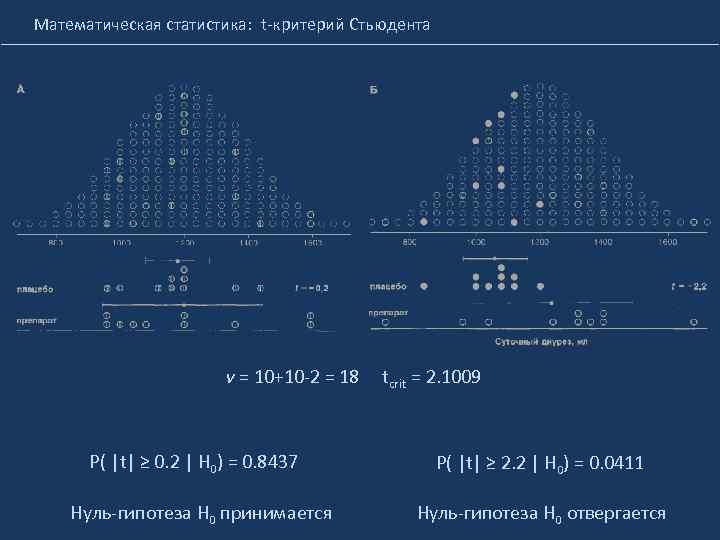Математическая статистика: t-критерий Стьюдента ν = 10+10 -2 = 18 tcrit = 2. 1009 P( |t| ≥ 0. 2 | H 0) = 0. 8437 P( |t| ≥ 2. 2 | H 0) = 0. 0411 Нуль-гипотеза H 0 принимается Нуль-гипотеза H 0 отвергается

Математическая статистика: t-критерий Стьюдента Итоговый алгоритм анализа 3. Рассчитать значение критерия t. 4. Определить число степеней свободы ν = n. X + n. Y -2 и выбрать уровень значимости α. 5. Рассчитать вероятность P( |t| ≥ tcrit | H 0) с использованием функции распределения Стьюдента либо найти критическое значение tcrit по таблице распределения Стьюдента 6. Если P < α либо если |t| > tcrit, нуль-гипотеза об отсутствии различий отвергается.

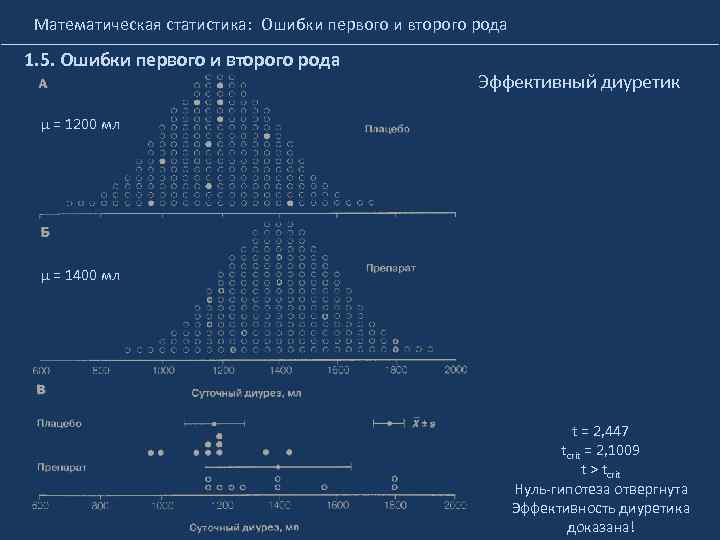Математическая статистика: Ошибки первого и второго рода 1. 5. Ошибки первого и второго рода Эффективный диуретик μ = 1200 мл μ = 1400 мл t = 2, 447 tcrit = 2, 1009 t > tcrit Нуль-гипотеза отвергнута Эффективность диуретика доказана!

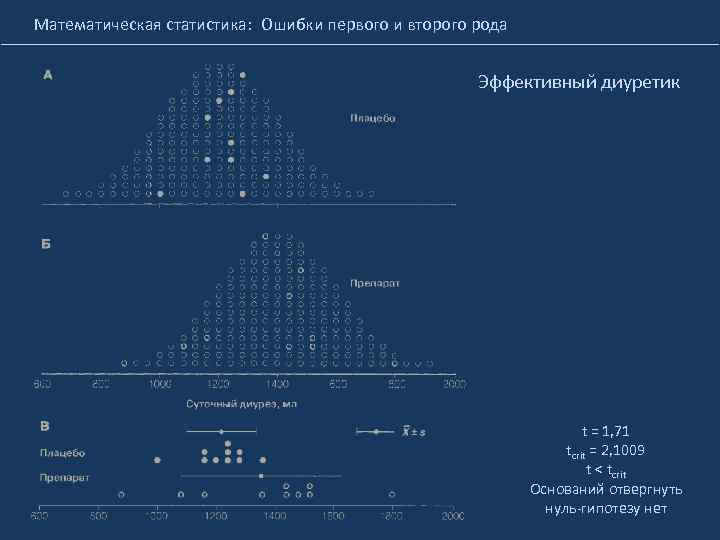Математическая статистика: Ошибки первого и второго рода Эффективный диуретик t = 1, 71 tcrit = 2, 1009 t < tcrit Оснований отвергнуть нуль-гипотезу нет

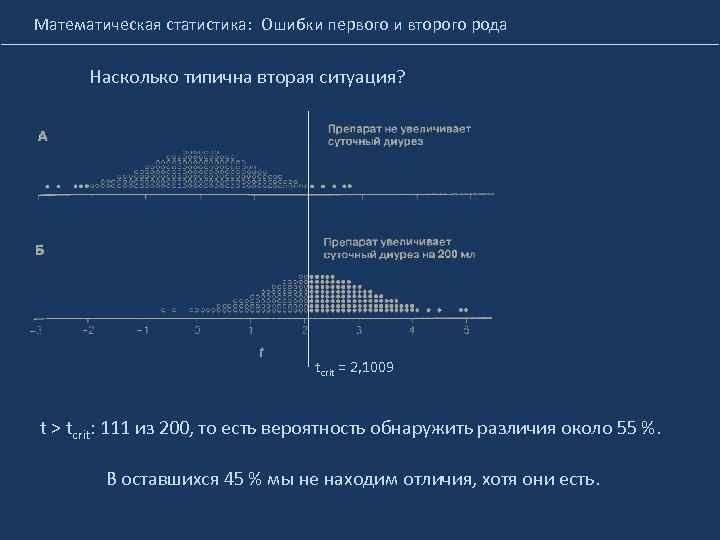Математическая статистика: Ошибки первого и второго рода Насколько типична вторая ситуация? tcrit = 2, 1009 t > tcrit: 111 из 200, то есть вероятность обнаружить различия около 55 %. В оставшихся 45 % мы не находим отличия, хотя они есть.

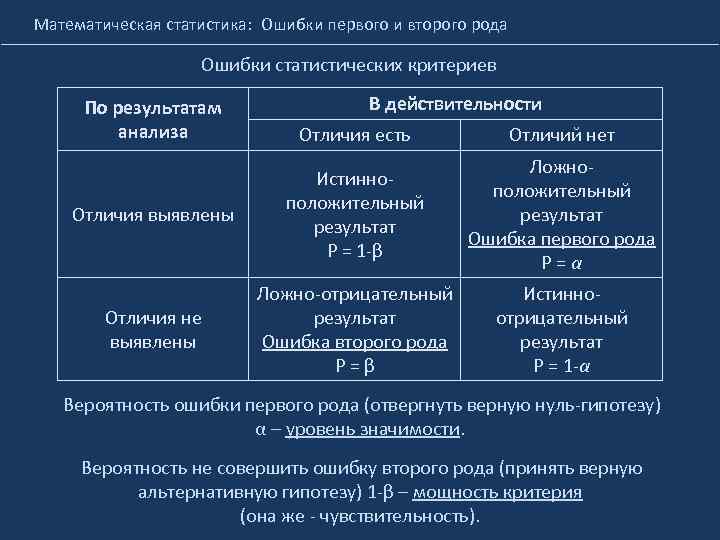Математическая статистика: Ошибки первого и второго рода Ошибки статистических критериев По результатам анализа В действительности Отличия есть Отличий нет Отличия выявлены Истинноположительный результат P = 1 -β Ложноположительный результат Ошибка первого рода P = α Отличия не выявлены Ложно-отрицательный результат Ошибка второго рода P = β Истинноотрицательный результат P = 1 -α Вероятность ошибки первого рода (отвергнуть верную нуль-гипотезу) α – уровень значимости. Вероятность не совершить ошибку второго рода (принять верную альтернативную гипотезу) 1 -β – мощность критерия (она же - чувствительность).

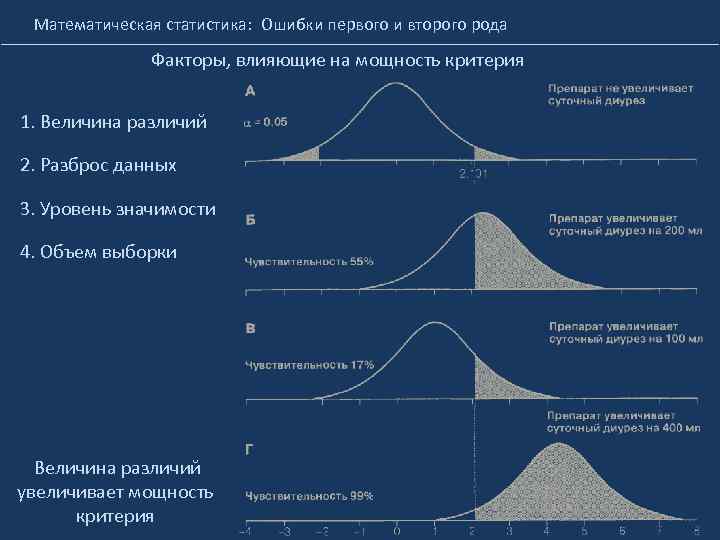Математическая статистика: Ошибки первого и второго рода Факторы, влияющие на мощность критерия 1. Величина различий 2. Разброс данных 3. Уровень значимости 4. Объем выборки Величина различий увеличивает мощность критерия

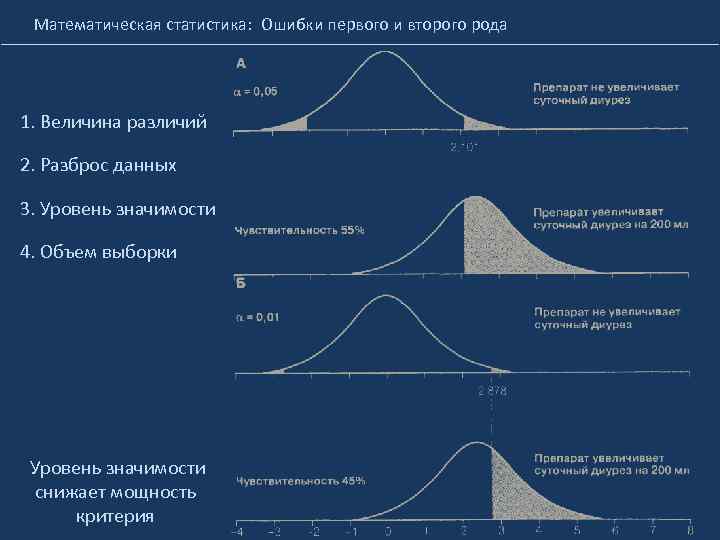Математическая статистика: Ошибки первого и второго рода 1. Величина различий 2. Разброс данных 3. Уровень значимости 4. Объем выборки Уровень значимости снижает мощность критерия

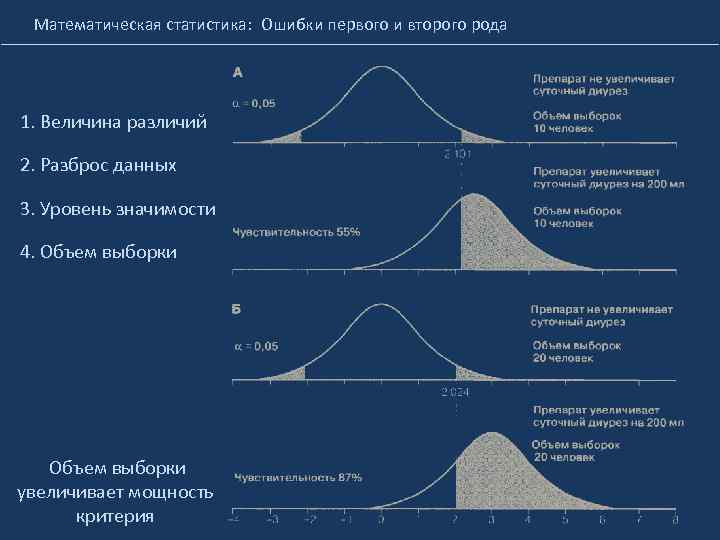Математическая статистика: Ошибки первого и второго рода 1. Величина различий 2. Разброс данных 3. Уровень значимости 4. Объем выборки увеличивает мощность критерия

Математическая статистика: Доверительные интервалы 1. 6. Доверительные интервалы 1 - α = 95 % α = 5 %

Математическая статистика: Доверительные интервалы Доверительный интервал – область, в которую с заданной вероятностью (1 – α) попадает оцениваемый параметр. (квантиль распределения Стьюдента с ν = n-1 степенями свободы) (в таблицах для двустороннего варианта критерия следует выбирать значение для α)