Математические методы моделирования в геологии Надо производить опыты

Математические методы моделирования в геологии Надо производить опыты, изменяя обстоятельства, пока не извлечем из них общее правило, потому что опыт доставляет истинное правило. Леонардо да Винчи. 2014 Лекция 3

Нормальное распределение. Функция плотности вероятности нормального распределения ПВНР. Построение кривой ПВНР. Распространённый вид распределения г/г/ф параметров – нормальное распределение (распределение Гаусса): - функция ПВНР 2 параметра – М(х) и дисперсия. В идеале: кривая ПВНР симметричная колообразная с колокол максимумом в , мода и медиана совпадают. На практике: говорят: «данная кривая представлена для совокупности, распределение данных которой приближено к нормальному» .

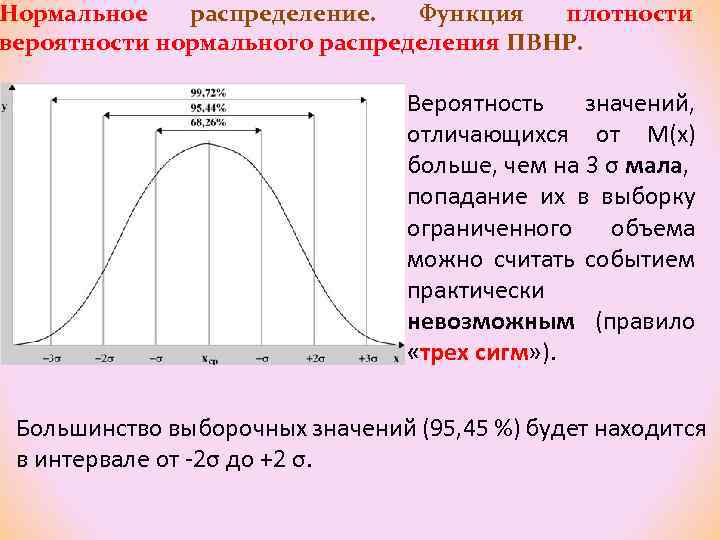Нормальное распределение. Функция плотности вероятности нормального распределения ПВНР. Вероятность значений, отличающихся от М(х) больше, чем на 3 σ мала, попадание их в выборку ограниченного объема можно считать событием практически невозможным (правило «трех сигм» ). Большинство выборочных значений (95, 45 %) будет находится в интервале от -2σ до +2 σ.

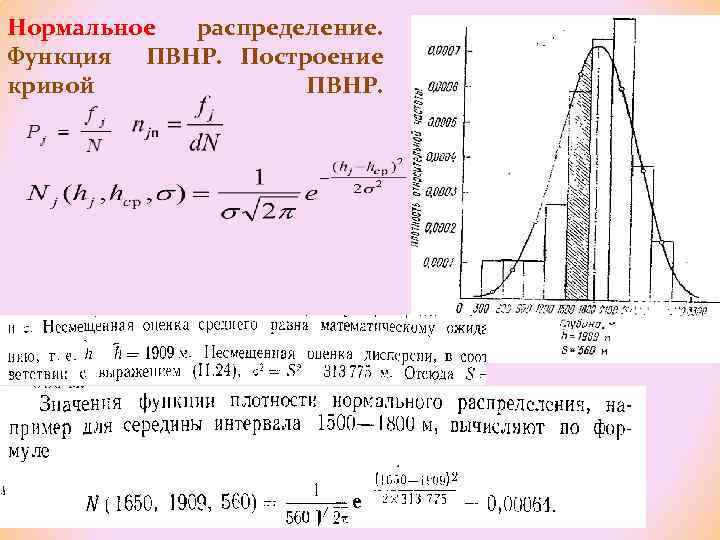Нормальное распределение. Функция ПВНР. Построение кривой ПВНР.

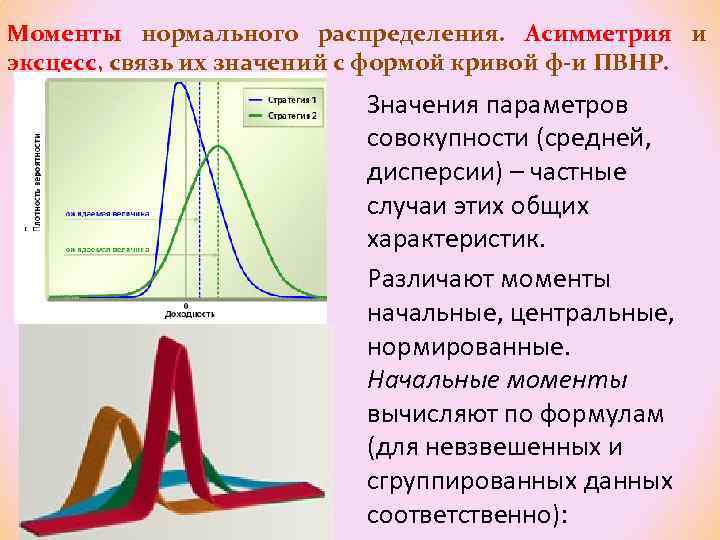Моменты нормального распределения. Асимметрия и эксцесс, связь их значений с формой кривой ф-и ПВНР. Значения параметров совокупности (средней, дисперсии) – частные случаи этих общих характеристик. Различают моменты начальные, центральные, нормированные. Начальные моменты вычисляют по формулам (для невзвешенных и сгруппированных данных соответственно):

Моменты нормального распределения. Асимметрия и эксцесс, связь их значений с формой кривой ф-и ПВНР. Начальные моменты (для невзвешенных сгруппированных, соответственно): и

Моменты нормального распределения. Асимметрия и эксцесс, связь их значений с формой кривой ф-и ПВНР. Центральные моменты - средние значения степеней отклонений СВ от математического ожидания:

Моменты нормального распределения. Асимметрия и эксцесс, связь их значений с формой кривой ф-и ПВНР. Нормированные моменты. К = 1, 2, 3, 4 (порядок).

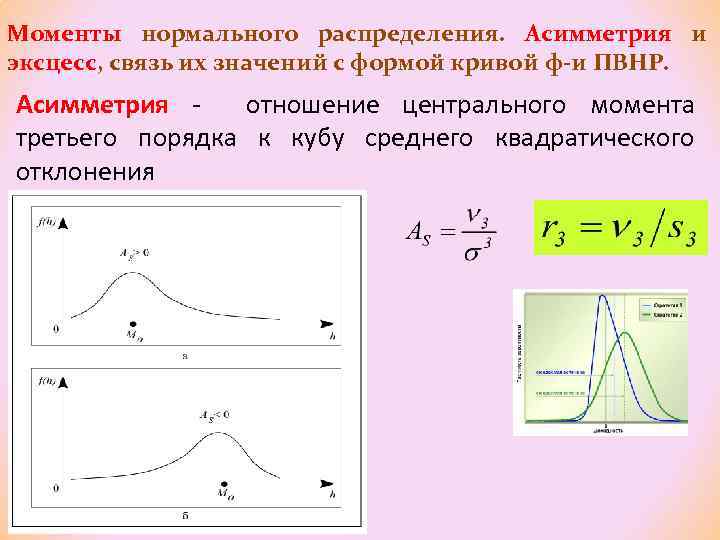Моменты нормального распределения. Асимметрия и эксцесс, связь их значений с формой кривой ф-и ПВНР. Асимметрия отношение центрального момента третьего порядка к кубу среднего квадратического отклонения

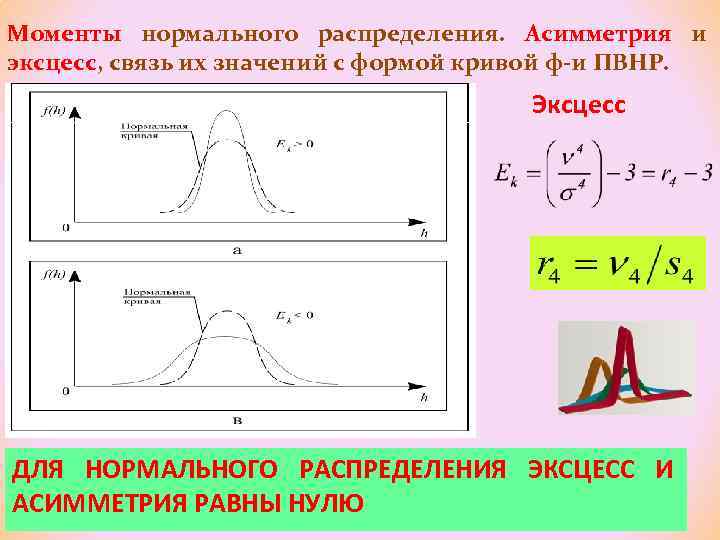Моменты нормального распределения. Асимметрия и эксцесс, связь их значений с формой кривой ф-и ПВНР. Эксцесс ДЛЯ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ ЭКСЦЕСС И АСИММЕТРИЯ РАВНЫ НУЛЮ

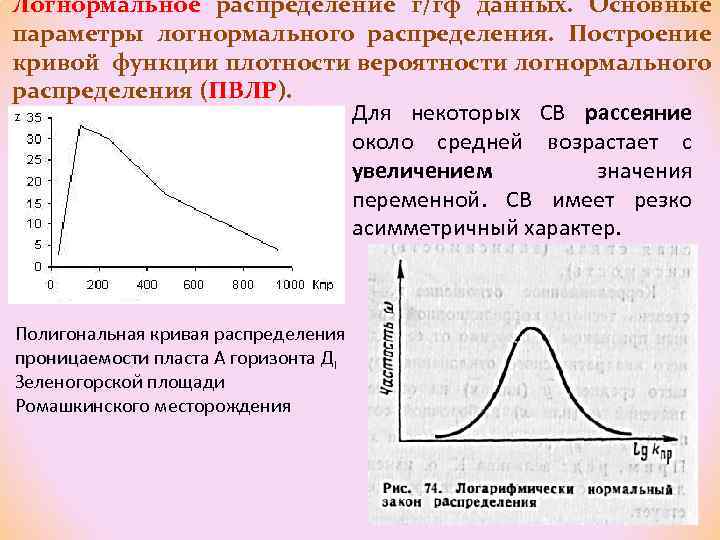Логнормальное распределение г/гф данных. Основные параметры логнормального распределения. Построение кривой функции плотности вероятности логнормального распределения (ПВЛР). Для некоторых СВ рассеяние около средней возрастает с увеличением значения переменной. СВ имеет резко асимметричный характер. Полигональная кривая распределения проницаемости пласта А горизонта ДI Зеленогорской площади Ромашкинского месторождения

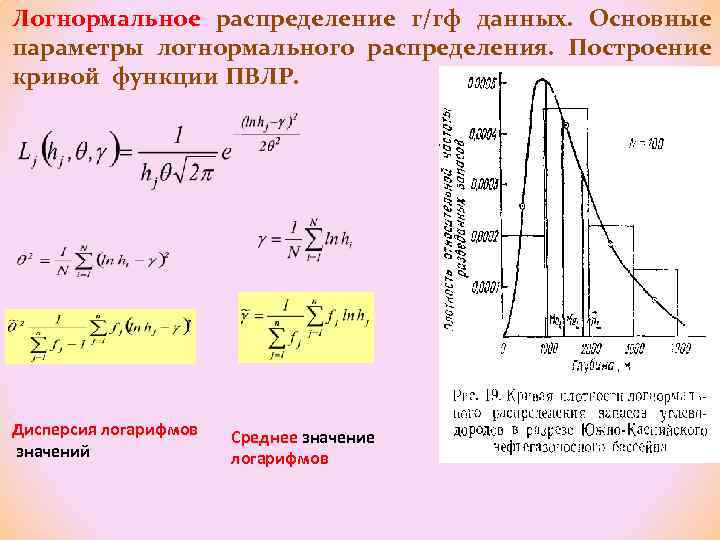Логнормальное распределение г/гф данных. Основные параметры логнормального распределения. Построение кривой функции ПВЛР. Дисперсия логарифмов значений Среднее значение логарифмов

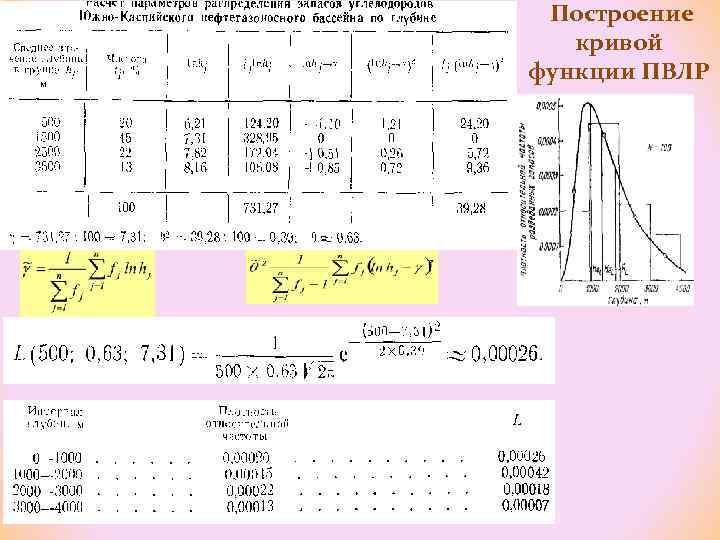Построение кривой функции ПВЛР

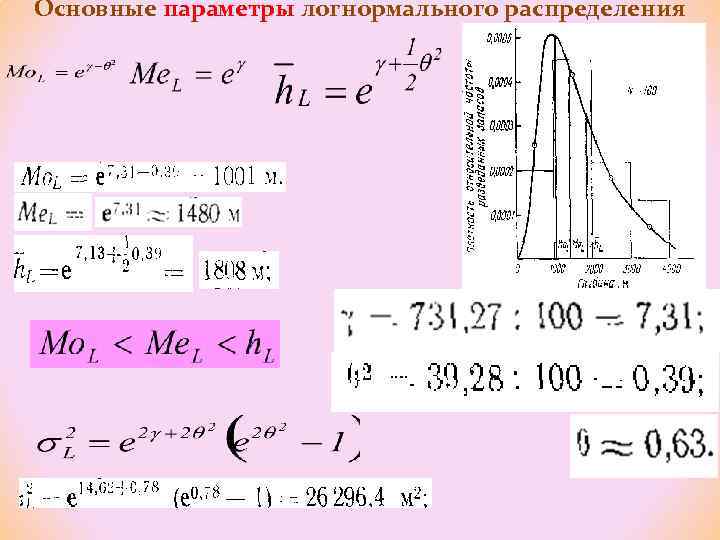Основные параметры логнормального распределения

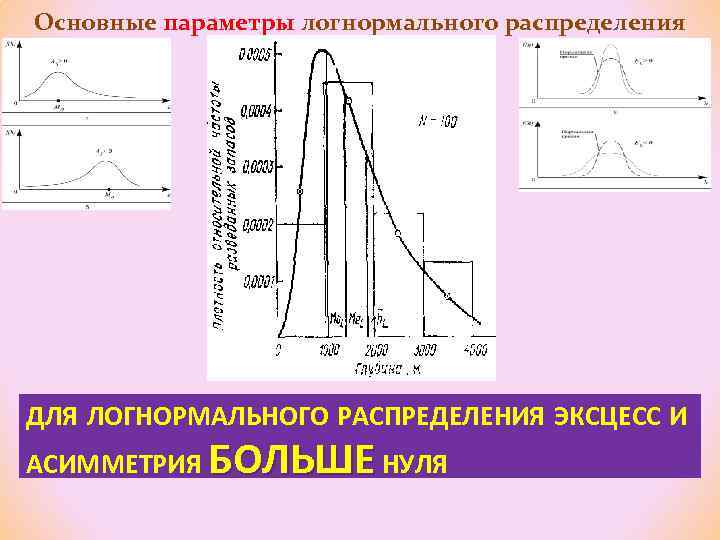Основные параметры логнормального распределения ДЛЯ ЛОГНОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ ЭКСЦЕСС И АСИММЕТРИЯ БОЛЬШЕ НУЛЯ

. Если все кажется легким – это безошибочно доказывает, что работник весьма мало искусен и что работа выше его разумения. Л. да Винчи.

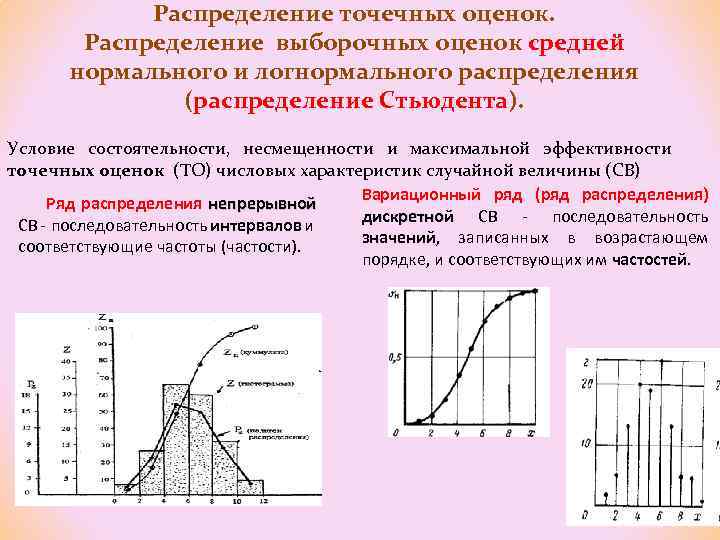Распределение точечных оценок. Распределение выборочных оценок средней нормального и логнормального распределения (распределение Стьюдента). Условие состоятельности, несмещенности и максимальной эффективности точечных оценок (ТО) числовых характеристик случайной величины (СВ) Вариационный ряд (ряд распределения) Ряд распределения непрерывной дискретной СВ - последовательность интервалов и значений, записанных в возрастающем соответствующие частоты (частости). порядке, и соответствующих им частостей.

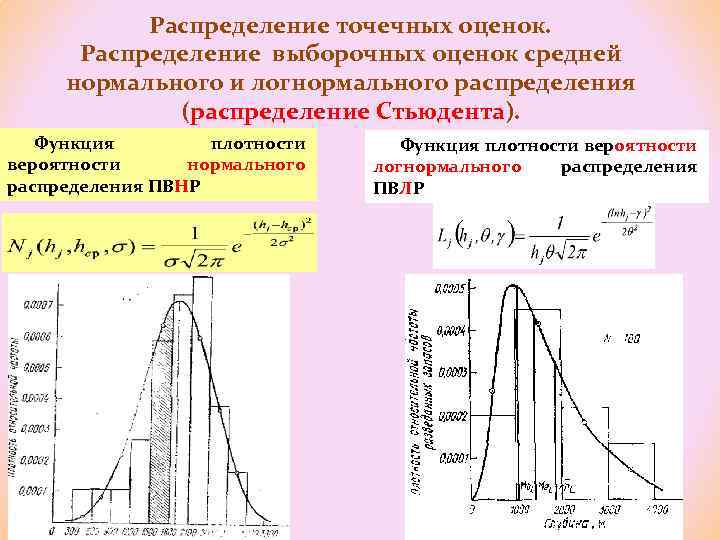Распределение точечных оценок. Распределение выборочных оценок средней нормального и логнормального распределения (распределение Стьюдента). Функция плотности вероятности нормального распределения ПВНР Функция плотности вероятности логнормального распределения ПВЛР

Распределение точечных оценок. Распределение выборочных оценок средней нормального и логнормального распределения (распределение Стьюдента). Точечные оценки (ТО, ) параметров распределения выборочной совокупности могут отличаться от истинных значений (T) параметра генеральной совокупности. Для разных выборок м. б. получены разные оценки. По Ɲ значениям выборочных оценок можно построить гистограмму. Она так же описывается тем или иным законом распределения.

Распределение точечных оценок. Распределение выборочных оценок средней нормального и логнормального распределения (распределение Стьюдента). Доказано: совокупность выборочных ТО среднего описывается законом, близком к нормальному. Чаще используют распределение Стьюдента, также приближающееся к нормальному закону при Ɲ→∞. Плотность вероятности распределения Стьюдента где m – число степеней свободы (единственный параметр распределения).

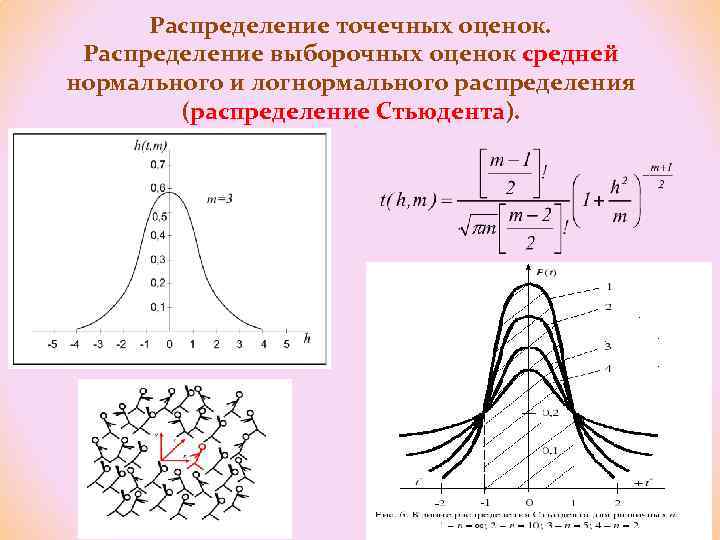Распределение точечных оценок. Распределение выборочных оценок средней нормального и логнормального распределения (распределение Стьюдента).

Распределение точечных оценок. Распределение доверительных интервалов выборочных оценок средней нормального и логнормального распределения (распределение Стьюдента). тем точнее определяет параметр , чем меньше величина разности | - |. >0 и | - |< , чем меньше , тем оценка точнее, характеризует точность оценки. Статистические методы не позволяют категорически утверждать «оценка удовлетворяет неравенству | - |< » Говорят «о вероятности , с которой неравенство | - |< осуществляется» . Надежность (доверительная вероятность) оценки по вероятность , с которой осуществляется неравенство | - |<. Число, близкое к единице (задают: 0, 95; 0, 99 и 0, 999).

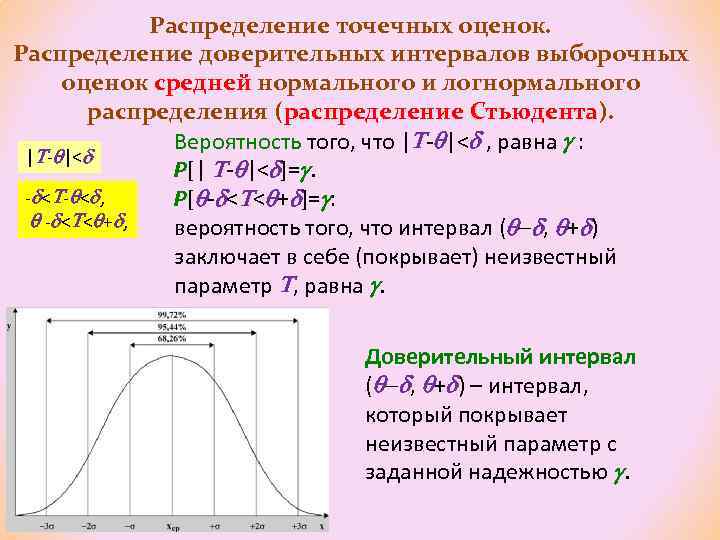Распределение точечных оценок. Распределение доверительных интервалов выборочных оценок средней нормального и логнормального распределения (распределение Стьюдента). Вероятность того, что | - |< , равна : | - |< P[| - |< ]=. - < , P[ - < < + ]= : - < < + , вероятность того, что интервал ( , + ) заключает в себе (покрывает) неизвестный параметр , равна . Доверительный интервал ( , + ) – интервал, который покрывает неизвестный параметр с заданной надежностью .

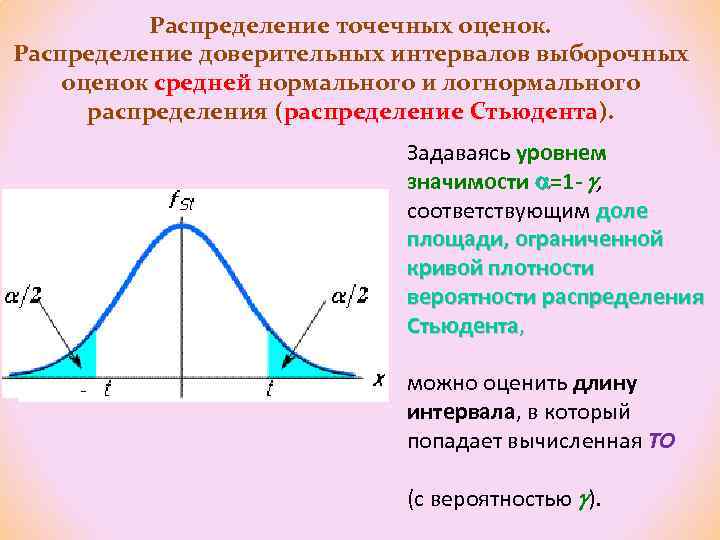Распределение точечных оценок. Распределение доверительных интервалов выборочных оценок средней нормального и логнормального распределения (распределение Стьюдента). Задаваясь уровнем значимости =1 - , соответствующим доле площади, ограниченной кривой плотности вероятности распределения Стьюдента, можно оценить длину интервала, в который попадает вычисленная ТО (с вероятностью ).

Распределение точечных оценок. Распределение доверительных интервалов выборочных оценок средней нормального и логнормального распределения (распределение Стьюдента). Обозначим через уровень значимости, при котором точечная оценка средней попадает с вероятностью =1 - в доверительный интервал, определим его длину по формуле где L – длина доверительного интервала; отсекаемая часть площади, ограниченная кривой распределения Стьюдента при m-1 степенях свободы. Среднее значение совокупности заключено в интервале