Математическая статистика Случайные величины Случайной называется величина

Математическая статистика Случайные величины

Случайной называется величина, которая в результате испытания может принять то или иное возможное значение, неизвестное заранее, но обязательно одно. Пример 1. В студенческой группе 25 человек. Пусть величина Х – число студентов, находящихся в аудитории перед началом занятий. Ее возможными значениями будут числа 0, 1, 2, …, 25. При каждом испытании (начало занятий) величина Х обязательно примет одно из своих возможных значений, т. е. наступит одно из событий Х = 0, Х = 1, …, Х = 25.

Для полной характеристики дискретной случайной величины мало знать ее значения. Необходимо им поставить в соответствие вероятности. Соответствие между всеми возможными значениями дискретной случайной величины и их вероятностями называется законом распределения данной случайной величины.

Простейшая формой задания закона распределения дискретной случайной величины является таблица, в которой перечислены возможные значения случайной величины (обычно в порядке возрастания) и соответствующие им вероятности: Х х1 х2 … хn … Р р 1 р 2 … р n … Такая таблица называется рядом распределения. Допустим, что число возможных значений случайной величины конечно: х1, х2, …, хn. При одном испытании случайная величина принимает одно и только одно постоянное значение. Поэтому события Х = хi (i = 1, 2, … , n) образуют полную группу попарно независимых событий. Следовательно, р1 + р2 + … + рn = 1.

Пусть из генеральной совокупности извлечена выборка, причём x 1 наблюдалось n 1 раз, х2 – n 2 раз, xk – nk раз и ni = n – объём выборки. Наблюдаемые значения xi называют вариантами, а последовательность вариант, записанных в возрастающем порядке – вариационным рядом. Числа наблюдений называют частотами, а их отношения к объему выборки – относительными частотами. Статическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот.

Пример 2 В результате 10 опытов случайная величина приняла следующие значения: 1, 1, 1, 4, 4, 5, 6, 6. Напишите таблицу закона распределения для нее х 1 4 5 6 n 3 2 1 4

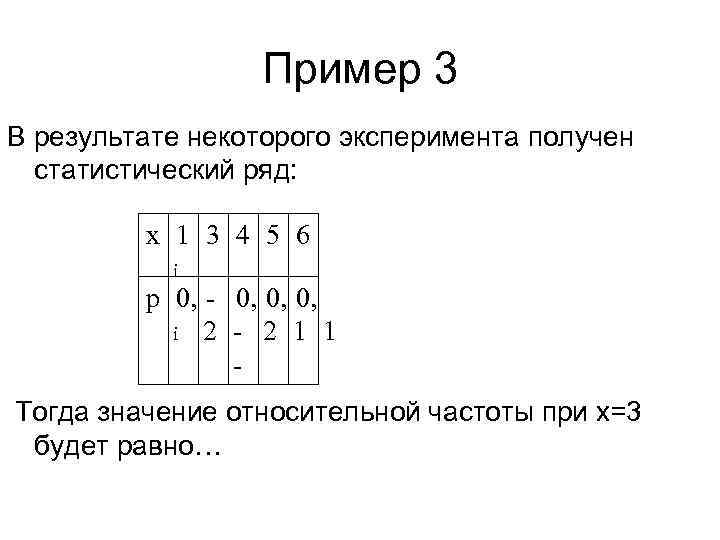Пример 3 В результате некоторого эксперимента получен статистический ряд: х 1 3 4 5 6 i p 0, - 0, 0, 0, i 2 - 2 1 1 Тогда значение относительной частоты при х=3 будет равно…

Пример 4 В результате 10 опытов случайная величина приняла следующие значения: 2, 2, 3, 4, 4, 4, 6, 6. Тогда закон распределения для нее представлен в таблице. Xi Pi 2 2 3 1 4 3 6 4 Xi Pi 2 0 3 1 4 1 6 0 Xi 2 3 4 6 Pi 0, 2 0, 1 0, 3 0, 4

Функция распределения вероятностей Непрерывную случайную величину нельзя охарактеризовать перечнем всех возможных ее значений и их вероятностей. Естественно, встает вопрос о том, нельзя ли охарактеризовать случайную величину иным способом, одинаково годным как для дискретных, так и для непрерывных случайных величин. Функцией распределения случайной величины Х называют функцию F(x), определяющую для каждого значения х, вероятность того, что случайная величина Х примет значение меньше х, т. е. F(x) = P (X

Числовые характеристики случайной величины Математическое ожидание случайной величины Х указывает некоторое среднее значение, около которого группируются все возможные значения Х. Для дискретной случайной величины, которая может принимать лишь конечное число возможных значений, математическим ожиданием называют сумму произведений всех возможных значений случайной величины на вероятность этих значений:

• Дисперсией случайной величины называется математическое ожидание квадрата ее отклонения от математического ожидания D(X) = M(X –М(Х))2.

Средним квадратическим отклонением случайной величины Х называется арифметический корень из дисперсии, т. е. σ(X) =

Пример 5 Дискретная случайная величина Х, имеющая смысл числа курьеров, задействованных для доставки корреспонденции в коммерческой организации, задана законом распределения: Х 0 1 2 3 0, 4 0, 1 0, 3 0, 2 Найти математическое ожидание, дисперсию, среднее квадратическое отклонение.

• Модой дискретной случайной величины, обозначаемой Мо, называется ее наиболее вероятное значение • Модой называется вариант, которому соответствует наибольшая частота.

• Медианой непрерывной случайной величины Х называется такое ее значение Ме, для которого одинаково вероятно, окажется ли случайная величина меньше или больше Ме, т. е. Р(Х < Ме) = Р(X > Ме) • Медианой называется значение признака, приходящееся на середину ранжированного ряда наблюдений.

Примеры 6, 7 1. Провели несколько измерений случайной величины: 3, 4; 1; 3; 0, 6; 3, 2; 3; 1, 2. Найдите среднее арифметическое, моду и медиану этого набора чисел. 2. Провели несколько измерений случайной величины: 3; 10; 2; 8; 10; 11; 8; 4. Найдите среднее арифметическое, моду и медиану этого набора чисел

Пример 8 • Дано следующее распределение дискретной случайной величины Х X 1 2 4 5 P 0. 31 0. 29 0. 3 • Найти ее математическое ожидание, дисперсию и среднеквадратичное отклонение, используя формулы для их определения.

Равномерное распределение Непрерывная случайная величина Х имеет равномерное распределение на отрезке [a, b], если ее плотность имеет следующий вид:

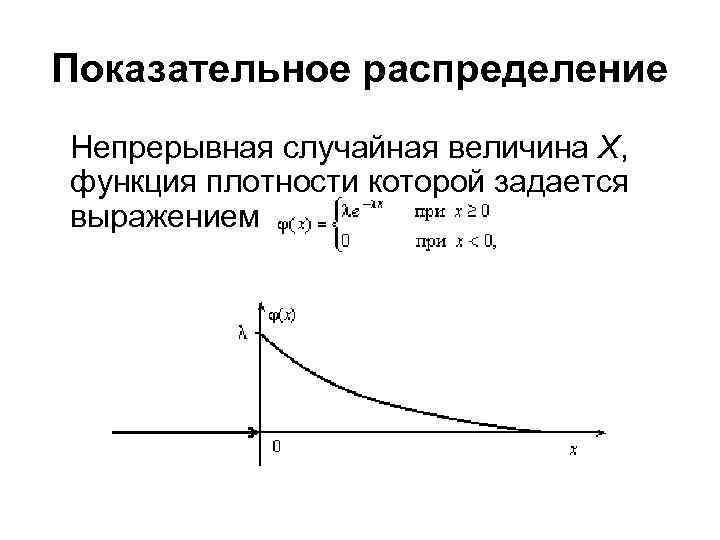Показательное распределение Непрерывная случайная величина Х, функция плотности которой задается выражением

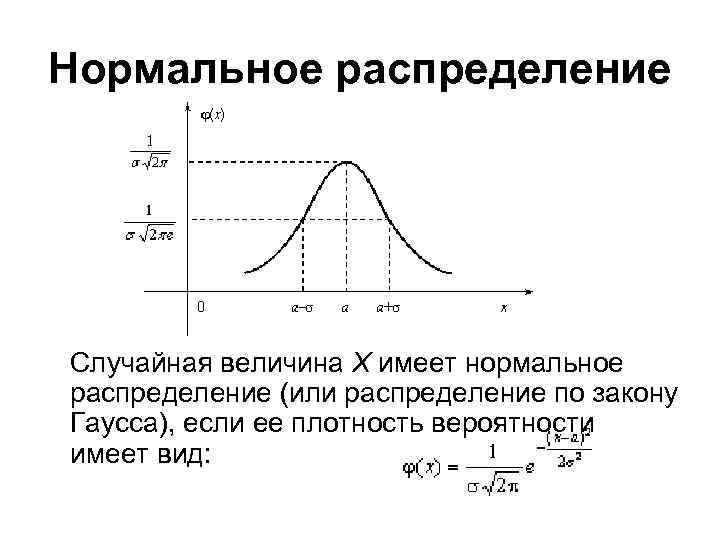Нормальное распределение Случайная величина Х имеет нормальное распределение (или распределение по закону Гаусса), если ее плотность вероятности имеет вид:

Выборка. Эмпирическая функция распределения Пусть в некотором опыте наблюдается случайная величина Х с функцией распределения F(x). И пусть однократное осуществление опыта позволяет нам найти одно из возможных ее значений. Предположим, что опыт в одних и тех же условиях можно повторять какое угодно число раз, и что сами опыты (испытания) являются независимыми. Результаты рассматриваемых n опытов представляют собой последовательность x 1, x 2, … , xn действительных чисел, которая называется выборкой объема n. Такова практическая трактовка выборки. Каждое xi (i=1, 2, …, n) называется вариантой(элементом выборки, наблюденным значением, значением признака).

Пример 9 Из генеральной совокупности извлечена выборка объема n=60, статистическое распределение этой выборки имеет вид x 2 3 5 i n 2 i 0 2 5 Тогда n 2 равно ….

Пример 10 По статистическому распределению выборки установите ее объем x 2 3 5 i n 1 2 2 i 0 0 5

Выборочная средная: