теория вероятности.ppt
- Количество слайдов: 87

МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

Случайные события Теория вероятностей изучает закономерности, возникающие в случайных экспериментах, раскрывает объективные закономерности, присущие массовым явлениям Случайные события- любые события или факты, относящиеся к результату эксперимента, которые могут происходить или не происходить. Произойдет данное событие или нет- определяет случай

Случайные события – результат эксперимент, его исходы Отдельные случайные события обозначаются прописными латинскими буквами A, D Не все случайные явления можно изучать методами теории вероятностей, а лишь те, которые могут быть воспроизведены в одних и тех же условиях Основной числовой характеристикой случайного события является его вероятность

Пример Испытание – подбрасывание монеты События – монета упала «орлом » или «решкой» Случайное событие – выпадение решки или орла Пусть производится серия испытаний, в каждом из которых может появиться или не появиться событие А. Если в результате испытание появилось событие А, то такой исход испытания называется благоприятным исходом.

Классификация событий по степени возможности Достоверное событие – событие, которое в результате опыта обязательно должно произойти. Выпадение не менее одного очка при бросании игральной кости. Невозможное событие – событие , которое не может иметь место в данном опыте. Выпадение более шести очков при бросании игральной кости. Два или несколько событий называются равновозможными, если нет оснований утверждать, что одно из них имеет больше шансов появится в результате опыта, чем другое. Выпадение орла или решки при однократном бросании монеты.

Классификация событий по характеру совместных связей События называются несовместными, если появление одного из них в данном опыте исключает возможность появления других. Получение студентом на экзамене по одной дисциплине оценок « 5» , « 4» , « 3» . События совместны – если появления одного из них в данном опыте не исключает возможности появления других. Получение студентом на экзаменах по 3 дисциплинам оценок « 5» , « 4» , « 3»

Вероятность события Вероятности события – численная мера, принимающая значения между 0 и 1 и характеризующая степень возможности появления события в данном опыте. Обозначается: P(A), где А- случайное событие Вероятности выпадения четного числа очков при бросании кости Р(А)=3/6=1/2

Классическое определение вероятности (по Лапласу) Вероятность случайного события А – число элементарных событий, благоприятствующих появления события А, деленному на все число элементов в наборе элементарных событий Р(А) = m/n 0<Р(а)<1

Недостатки классического определения вероятности Применимо лишь в тех случаях, когда число элементарных событий конечно. На практике это не всегда возможно. Предполагается, что все элементарные события равновероятны. На практике не всегда можно определить равновероятность наступления отдельных элементарных событий. С 17 по 19 века использовалось классическое определение вероятности. В настоящее время определение не дается, а используется понятие относительной частоты событий.

Элементы комбинаторики Комбинаторика – раздел математики, изучающий комбинации конечных множеств элементов различной природы При вычислении вероятности приходится использовать формулы комбинаторики

Формулы комбинаторики Размещение Перестановки Сочетания

Свойства сочетаний

Абсолютной частотой случайного события А в серии из N случайных опытов называется число NA , которое показывает, сколько раз в этой серии произошло событие А. Относительной частотой случайного события называют отношение числа появлений этого события к общему числу проведенных экспериментов: Где А случайное событие, N – раз проведено испытание и при этом событие А наступило в NA случаях

При статистическом определении, вероятностью события называют относительную частоту события при большом числе испытаний или число близкое к ней: Вероятность Р(А) выражает количественную меру появления события в данных сериях испытаний

Условная вероятность – вероятность одного события, вычисленная в предположении, что другое событие произошло. Вероятность события А 1 в предположении, что произошло событие А 2 обозначается Р(А 1/А 2) Два события называются независимыми, если вероятность появления каждого из них не зависит от того, имели ли место другие Два события называются зависимыми, если появление одного из них влияет на вероятность появления другого

Алгебра событий Суммой двух событий А 1 и А 2 называется событие А=А 1+А 2 Теорема: Вероятность суммы двух несовместных событий равняется сумме их вероятностей: Р(А 1+А 2)=Р(А 1)+Р(А 2) Теорема справедлива для любого числа несовместных событий:

Произведением нескольких событии называется событие, состоящие в совместном наступлении всех этих событии в результате испытания. Произведение обозначают A A Aи. B B, B, Теорема: Вероятность суммы двух совместных событии равняется сумме их вероятностей , уменьшенная на вероятность произведения этих событии. P P P A 1 A 2 P A 2

Теорема: Вероятность произведения взаимно независимых событии равна произведению их вероятностей. P P A 2 A 1 P Теорема: Вероятность произведения зависимых событии равна произведению вероятности одного события на условную вероятность другого события, вычисленную в предположении, что первое случайное событие уже произошло P A A A A A P P P A

Свойства операций сложения и умножения A коммутативность сложения. B B A A B C - ассоциативность сложения. C B A A коммутативность умножения. B B A A C B B A C ассоциативность умножения A C B C закон дистрибутивности. B A A

Вероятность появления хотя бы одного из событий Теорема: Вероятность появления хотя бы одного из событии A 1, A 2, An , независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событии P 1 q 2 qn A q 1 … Следствие: При производимых n одинаковых независимых испытаниях, в каждом из которых события A появляется с вероятностью p , вероятность появления события A хотя бы один раз равна P 1 p A 1 n

Диаграммы Эйлера - Венна Диаграмма, иллюстрирующая сумму совместных событий Диаграмма, иллюстрирующая сумму несовместных событий

Диаграмма, иллюстрирующая сумму трех совместных событий Диаграмма, иллюстрирующая произведение совместных событий

Формула Бейеса Следствием двух основных теорем теории вероятности ( теорем сложения и умножения) являются формула Бейеса и формула полной вероятности. Формула Бейеса дает возможность оценить вероятность эмпирическим путем, а так же корректировать управленческие решения в экономике, оценки неизвестных параметров распределения изучаемых признаков в статистическом анализе

Где: Нi – гипотезы (события в условиях которых только и может появиться событие А) вероятность осуществления гипотез в предположении, что событие А произошло вероятность появления события А (условные вероятности)

Формула полной вероятности Полная вероятность события равна сумме произведений вероятности гипотез на условные вероятности события, вычисленные при каждой из гипотез.

Случайные величины Случайная величина – величина, которая в результате опыта может принять то или иное значение, но неизвестно заранее какое именно. Случайная величина – числовая функция от случайного события, определенное обобщение понятия случайного события. Принятие случайной величиной конкретного значения представляет собой событие. Случайные величины обозначают заглавными буквами X , Y , Z , а их всевозможные значения, малыми x, y, z

Классификация случайных величин дискретные случайные величины непрерывные случайные величины. Дискретная случайная величина – величина, возможные значения которой отделимы друг от друга, принимающая конечное или счетное множество значении. Непрерывная случайная величина – величина, возможные значения которой неотделимы друг от друга и непрерывно заполняют некоторый интервал.

Полное описание случайной величины дает закон ее распределения. Закон распределения вероятностей случайной величины – соотношение, устанавливающее связь между вероятностями, с которыми случайная величина принимает различные значения и самими возможными значениями случайной величины. Закон распределения может быть представлен в виде: таблицы, аналитической зависимости графика

Ряд распределения - закон распределения вероятностей дискретной случайной величины, заданный в виде таблицы, в первой строке даны значения СВ, а во второй – соответствующие им вероятности. хi 0 1 2 pi 0. 12 0. 46 0. 42 Простейшая форма закона распределения дискретной случайной величины - ряд.
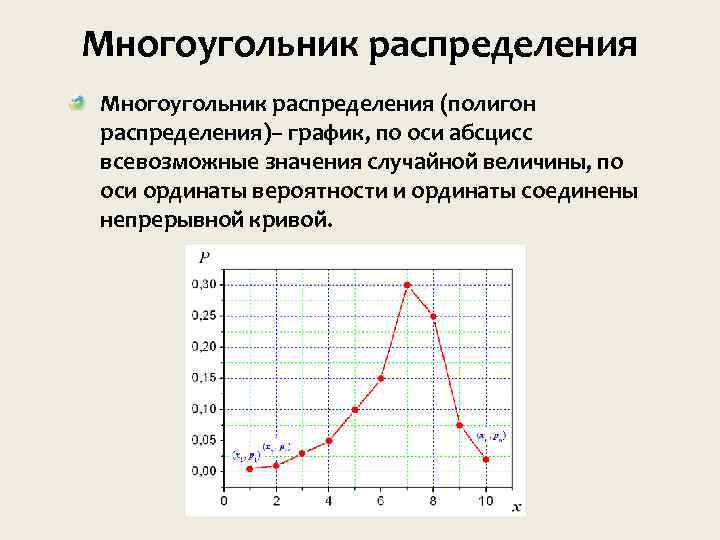
Многоугольник распределения (полигон распределения)– график, по оси абсцисс всевозможные значения случайной величины, по оси ординаты вероятности и ординаты соединены непрерывной кривой.

Замечания Сумма ординат многоугольника распределения или сумма всех возможных значении случайной величины всегда равна 1 При построении многоугольника распределения надо помнить, что соединение полученных точек носит условный характер. В промежутках между значениями случайной величины вероятность не принимает никакого значения. Точки соединены только для наглядности.

Интегральный закон распределения Функцией распределения F(x) случайной величины X называется вероятность того, что случайная величина примет значение, меньшее x : F P x X x

Свойства функции распределения 0 x F 1. Так как функция распределения представляет собой вероятность, она может принимать только те значения, которые принимает вероятность. Функция распределения является неубывающей функцией F F x 2 x 1 при x 2 x 1

Вероятность того, что случайная величина примет значение из интервала , равна разности a, b значении функции распределения на концах интервала: P F F a X b b a
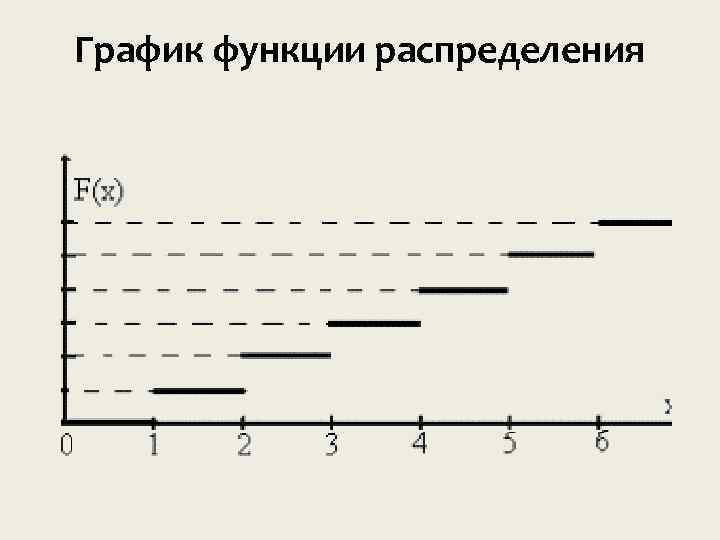
График функции распределения

Числовые характеристики положения случайной величины Характеристики положения дают представление о положении случайной величины на числовой оси. К ним относятся: Математическое ожидание Мода Медиана

Математическое ожидание – величина, равная сумме произведении отдельных значении , которые может принимать переменная на соответствующие им вероятности: Математическое ожидание – основная характеристика распределения. Она информирует о том, каков средний уровень значении , принимаемых случайной величиной. Математическое ожидание – число, около которого колеблются значения случайных величин и их средние значения по сериям опытов.

Свойства математического ожидания Мат. ожидание линеи но Математическое ожидание - взвешенное среднее, так как оно приближенно равно среднему арифметическому наблюдаемых значении случаи нои величины при большом числе опытов. Математическое ожидание не меньше наименьшего возможного значения случаи нои величины и не больше наибольшего. Математическое ожидание дискретнои случаи нои величины есть неслучаи ная (постоянная) величина

Свойства математического ожидания Математическое ожидание дискретнои случаи нои величины X может не совпадать ни с одним из ее возможных значении. Математическое ожидание постояннои равно самои постояннои Постоянныи множитель можно выносит за знак математического ожидания Математическое ожидание случаи нои величины определяет положение центра распределения вероятностеи. Математическое ожидание произведения (суммы) двух независимых случаи ных величин равно произведению (сумме) их математических ожидании

Мода, медиана Мода –значение случаи нои величины xi , имеющее наибольшую вероятность или наиболее вероятное значение. Обозначается m 0. Геометрически медиана – абсцисса точки (ось х), в которои площадь, ограниченная кривои распределения делится пополам. Все три характеристики (математическое ожидание, мода и медиана) не совпадают.

Характеристики рассеивания Значения наблюдаемых в практике с. в. всегда колеблются около среднего значения. Это явление называется рассеиванием величины около ее среднего значения. Числовые характеристики, описывающие это явление называются характеристиками рассеивания и основные из них: дисперсия среднее квадратичное отклонение.

Дисперсия – характеристика возможных отклонении с. в. от ее среднего значения. Чем большие отклонения в обе стороны от среднего значения возможны у даннои с. в. и чем больше вероятности таких отклонении , тем больше дисперсия с. в. В частном случае, когда среднее значение равно нулю, дисперсия характеризует разброс значении с. в. в обе стороны от нуля.

Свойства дисперсии Дисперсия принимает только положительные значения

Среднеквадратическое отклонение –корень квадратныи из дисперсии Начальным моментом k - порядка сл. величины Х называется математическое ожидание k степени этои величины. Центральным моментом k-го порядка сл. Величины (μ) Х называется математическое ожидание k степени отклонение сл. величины Х от ее мат. ожидания. k - первыи начальныи момент – мат. ожидание 1 k - второи центральныи момент – дисперсия. 2
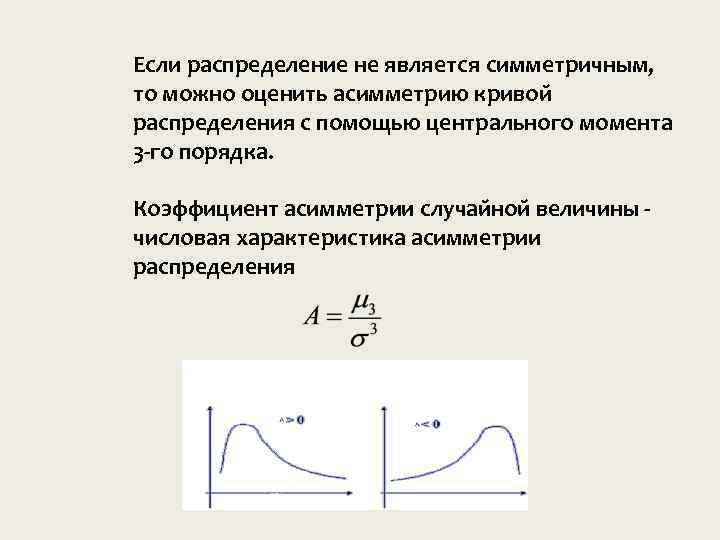
Если распределение не является симметричным, то можно оценить асимметрию кривои распределения с помощью центрального момента 3 -го порядка. Коэффициент асимметрии случаи нои величины числовая характеристика асимметрии распределения

Четвёртый центральныи момент – служит для характеристики крутости распределения. Эксцесс - числовая характеристика крутости распределения E>0 Е=0 Е<0

Законы распределения дискретной случайной величины Двухточечное распределение Биноминальное распределение(закон Бернулли) Распределение Пуассона

Двухточечное распределение Пусть вероятность некоторого случаи ного события A равна p , где 0 X - сл. вел. – число p 1. наступлении сл. события A в одном испытании. X сл. вел может принять одно из двух значении 0 – если сл. событие A не наступило, 1 – если оно произошло.

Закон распределения вероятностей сл. вел. , имеющей двухточечное распределение можно записать следующим образом: P 1 P p X 0 p X 1 Математическое ожидание этой случайной величины будет M 0 1 1 X p p p Дисперсия D M 2 2 X X M X

Биноминальное распределение (закон Бернулли) Данное распределение описывает ситуацию последовательного осуществления ряда независимых опытов с одинаковыми возможными исходами при каждом из них. Например, если производится группа выстрелов по одной и тои же цели, нас интересует не результат каждого выстрела, о общее число попадании.

Найдём вероятность P - вероятность того, что X m событие A наступит в m испытаниях. Таким образом, закон распределения будет P m m m n X Cn p 1 m p где m 0, 1, …, n, n-известное количество всех проведенных испытании , m -число тех испытании , в которых произошло событие A, p -вероятность появления события A в одном опыте.

ДСВХ, которая может принимать только целые неотрицательные значения с вероятностью m Pn P m X m m pmqn , Cn где p q 1 m 0, 1, 2, 3, …, n , называется распределённой по биноминальному закону, а p – параметром биноминального распределения. Функция распределения определяется формулой

Числовые характеристики биноминального распределения Математическое ожидание M(X)=np Дисперсия D p X np 1 npq Дисперсия имеет максимальное значение при p , и 1/2 наоборот, чем более p отличается от p , тем 1/2 дисперсия меньше. Вывод: Для того чтобы случайная величина была распределена по закону Бернулли необходимо, чтобы все контролируемые факторы были неизменные, а испытания не должны зависеть друг от друга.

Закон Пуассона используют в технических исследованиях ДСВХ, которая принимает целые неотрицательные значения с вероятностями, вычисляемыми по формуле Пуассона: P X m m /m!) e ( называется распределённой по закону Пуассона, где np – параметр распределения.

Числовые характеристики пуассоновского распределения Математическое ожидание и дисперсия M X np D X np Отличительная особенность данного распределения состоит в том, что математическое ожидание и дисперсия равны параметру распределения np, X т. е. M np X X D .

Свойства распределения Пуассона 1. Вероятность того, что событие не появится ни разу при m 0 P e 0 2. Вероятность того, что событие появится хотя бы один раз P 1 0 1 P 1 e 3. Вероятность того, что сл. величина примет значение не меньшее заданного k P k k 1 1 Pk X Pk P 1 … P 0 P … 1

Свойства распределения Пуассона 4. Закон Пуассона приближенное выражение формулы Бернулли, когда число опытов велико, а вероятность наступления события в каждом из них мала. От этого свойства закона Пуассона – выражать биноминальное распределение при большом числе опытов и малой вероятности события происходит и его другое название - закон редких явлении. Изучается редкий случаи , когда вероятность появления случайного события в одном испытании p 1. Теоретически считается, что p 0.

Непрерывные случайные величины Непрерывная случайная величина (НСВ) случайная величина, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Множество возможных значении непрерывной случайной величины бесконечно и несчетно.

Функция распределения непрерывной случайной величины Непрерывную случайную величину можно задать с помощью функции распределения функция плотности функция распределения

Функция плотности непрерывной случайной величины Законом распределения вероятностей непрерывной случайной величины – называют зависимость плотности от x. В такой форме закон распределения вероятностей непрерывной случайной величины называется дифференциальным.

Функция f (x) , называемая плотностью распределения непрерывной случайной величины, определяется по формуле: f(x)=F’(x) Где F - функция распределения. x Функция плотности показывает как часто появляется случайная величина X в некоторой окрестности точки x при повторении опытов.
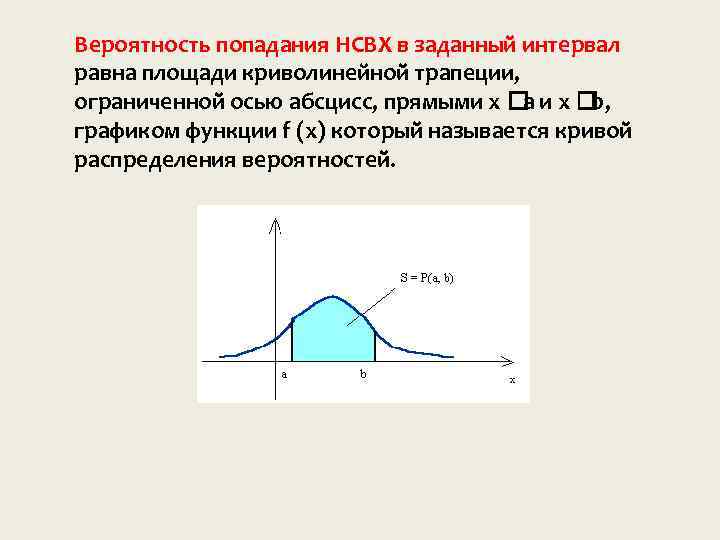
Вероятность попадания НСВХ в заданный интервал равна площади криволинейной трапеции, ограниченной осью абсцисс, прямыми x a b, графиком функции f (x) который называется кривой распределения вероятностей.

Условия нормировки плотности Условия нормировки

Свойства функции плотности распределения Функция плотности неотрицательна f (x) , так как 0 функция распределения является неубывающей. Функция распределения Вероятность попадания случайной величины в интервал определяется формулой a, b

Свойства функции распределения Условия нормировки График плотности распределения представляет собой кривую, расположенную выше оси Ох Если все возможные значения непрерывной случайной величины сосредоточены на интервале [a, b], то все интегралы вычисляются в этих пределах, а вне интервала f(x) . 0

Числовые характеристики непрерывной случайной величины Мода – числовая характеристика, определяющая наиболее вероятностное значение для непрерывной случайной величины, то значение, в котором плотность максимальна. Обозначается M 0 Медиана – это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам. Обозначается Ме В случае симметричного распределения медиана совпадает с математическим ожиданием и модой.

Математическое ожидание M непрерывной x случайной величины x , возможные значения которой принадлежат отрезку - числовая a, b характеристика, выраженная определенным интегралом

Дисперсия непрерывной случайной величины X числовая характеристика возможные значения которой принадлежат отрезку , вида: a, b Среднее квадратическое отклонение - числовая характеристика, равная корню квадратному из дисперсии

Законы распределения непрерывных случайных величин равномерный закон распределения нормальный (Гаусса), логарифмически нормальный , Веи булла, экспоненциальныи (показательный )

Равномерный закон распределения Закон распределения непрерывной случайной величины называется равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение Для того чтобы случайная величина подчинялась закону равномерного распределения необходимо, чтобы ее значения лежали внутри некоторого определенного интервала, и внутри этого интервала значения этой случайной величины были бы равновероятны.

Плотность равномерного распределения имеет вид

График плотности распределения
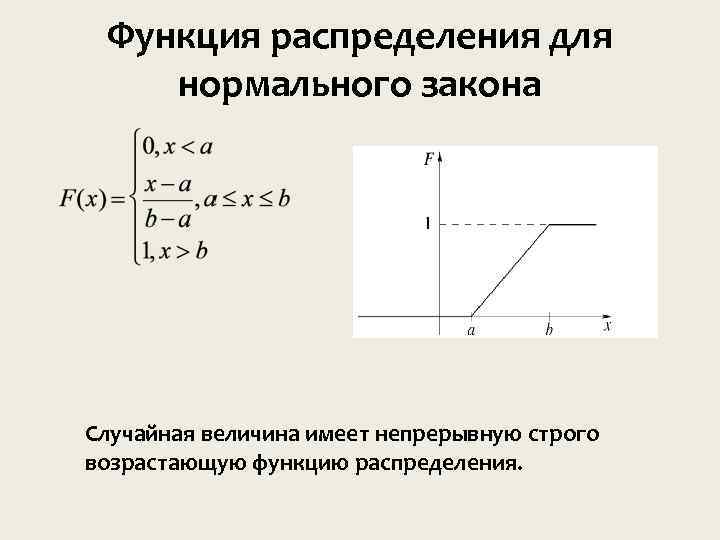
Функция распределения для нормального закона Случайная величина имеет непрерывную строго возрастающую функцию распределения.

Замечания Мода равномерного распределения – любое число из отрезка a, b Коэффициент асимметрии равен нулю Коэффициент эксцесса равен -6/5. Медиана совпадает с математическим ожиданием.

Экспоненциальное распределение является одним из основных распределении , используемых в теории надежности. Например, продолжительность безотказной работы многих технических устройств, а также время задержки вылета самолёта по вине технических служб аэропорта удовлетворительно описываются соответствующими экспоненциальными распределениями. Экспоненциальное распределение описывает наработку до отказа объектов.

Плотность и функция распределения Случайная величина x имеет экспоненциальное (показательное) распределение с параметром 0 , если плотность распределения
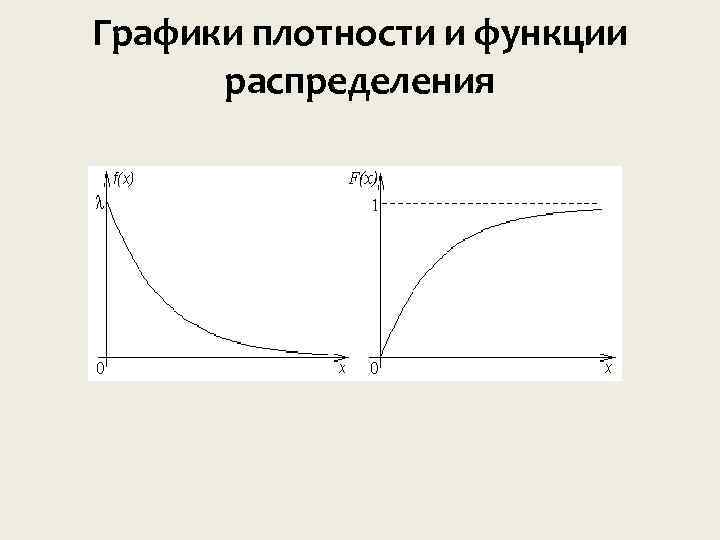
Графики плотности и функции распределения

Замечания Коэффициент асимметрии равен 2 Коэффициент эксцесса равен 6. Медиана равна ln / 2 Экспоненциального распределения имеет одинаковое математическое ожидание и среднее квадратичное отклонение. Вероятность попадания случайной величины в заданный интервал. P(a b) x F(b) F(a) e e a b

Числовые характеристики экспоненциального распределения

Закон Вейбулла Распределение Веи булла подходит для ряда механических объектов (к примеру, шарикоподшипников), оно может быть использовано при ускоренных испытаниях объектов в форсированном режиме. Случайная величина X имеет распределение Веи булла с параметрами m и a , если плотность распределения
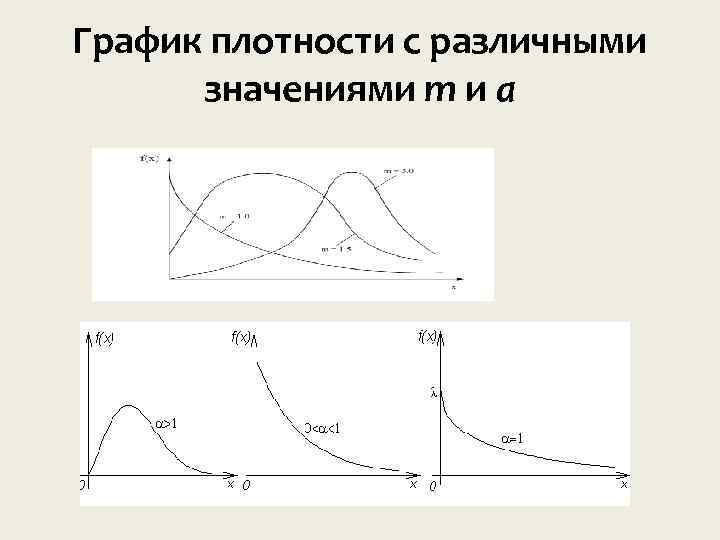
График плотности с различными значениями m и a

Замечания При m распределение Веи булла преобразуется в 1 экспоненциальное, При m 2, 5…. 3, 5 и a 0, 3…. . 0, 4 - приближается к нормальному. Если a , то распределение Веи булла 1 превращается в показательное распределение.

Функция распределения

Нормальное распределение (закон Гаусса) Это—наиболее часто встречающийся на практике закон распределения. Он является предельным законом, к которому приближаются другие законы распределения при часто встречающихся типичных условиях. Нормальный закон - это двухпараметрический закон, для записи которого нужно знать математическое ожидание и среднее квадратичное отклонение.
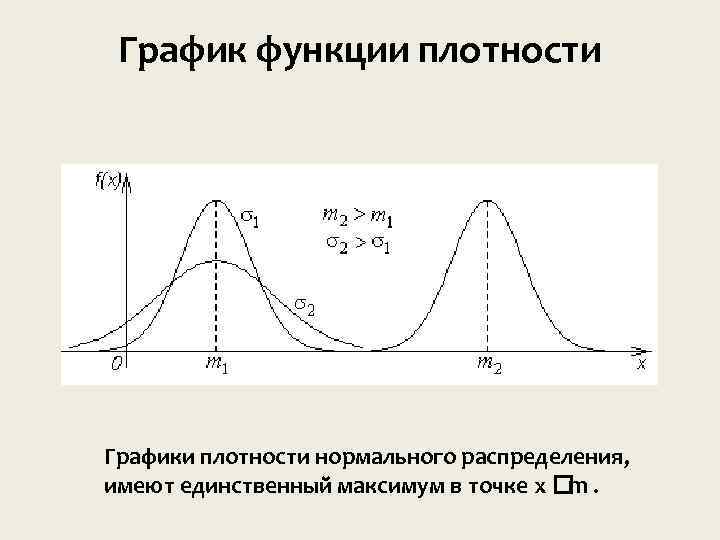
График функции плотности Графики плотности нормального распределения, имеют единственный максимум в точке x . m
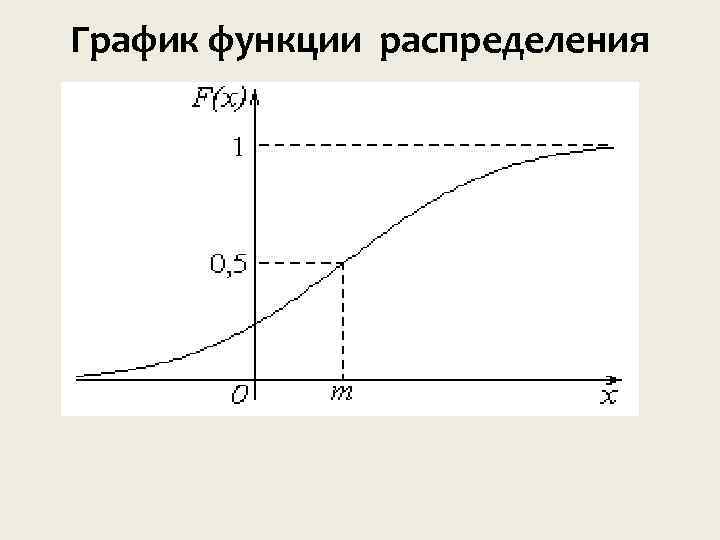
График функции распределения

Функция Лапласа или интеграл вероятностей 1. 2. 3. 4. Ф(х) определена при всех значениях х Ф(х) = 0 Ф(х) монотонно возрастает при всех значениях х Ф(х)- нечетная функция: Ф(-х) = -Ф(х)
теория вероятности.ppt