Скачать презентацию Математическая статистика Описание данных Статистическое оценивание Проверка Статистических Скачать презентацию Математическая статистика Описание данных Статистическое оценивание Проверка Статистических

Лекция_вводная.ppt

  • Количество слайдов: 43

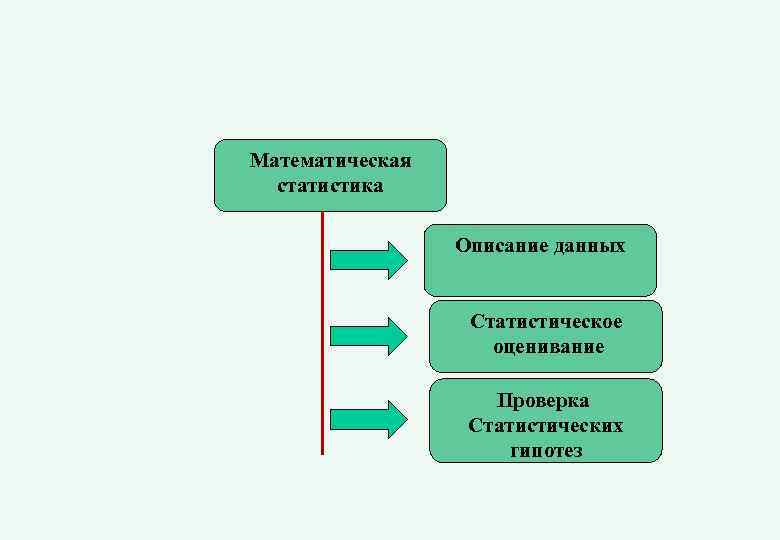Математическая статистика Описание данных Статистическое оценивание Проверка Статистических гипотез Математическая статистика Описание данных Статистическое оценивание Проверка Статистических гипотез

Математическая статистика – область науки, разрабатывающая математические методы для изучения количественных характеристик массовых явлений. Математическая статистика – область науки, разрабатывающая математические методы для изучения количественных характеристик массовых явлений. Составными частями математической статистики являются: (1) описание данных, (2) статистическое оценивание и (3) проверка статистических гипотез.

Данные (data) – представляют собой результаты наблюдений, испытаний, накапливаемые с целью последующего изучения и Данные (data) – представляют собой результаты наблюдений, испытаний, накапливаемые с целью последующего изучения и анализа. Переменная, признак (variable) – это некоторая общая для всех изучаемых объектов характеристика или свойство, конкретные проявления которых могут меняться от объекта к объекту. Проявление признака называют значениями, альтернативами, градациями. Измеряется не сам объект, а его отдельные параметры, характеристики.

Распределение переменной (distribution of the variable) – совокупность различных значений, которые переменная принимает для Распределение переменной (distribution of the variable) – совокупность различных значений, которые переменная принимает для различных изучаемых объектов. Генеральная совокупность (population) – вся интересующая исследователя совокупность изучаемых объектов. Выборка, выборочная совокупность (sample) – некоторая, обычно небольшая, часть генеральной совокупности, отбираемая специальным образом и исследуемая с целью получения выводов о свойствах генеральной совокупности

Параметры (parameters) – числовые характеристики генеральной совокупности Статистики (statistics) – числовые характеристики выборки. Параметры (parameters) – числовые характеристики генеральной совокупности Статистики (statistics) – числовые характеристики выборки.

Описательная статистика (descriptive statistics) – состоит из статистических методов, которые позволяют проводить сбор, упорядочение, Описательная статистика (descriptive statistics) – состоит из статистических методов, которые позволяют проводить сбор, упорядочение, обобщение и визуализацию данных. Аналитическая статистика (inferential statistics) – состоит из методов, которые на основе изучения статистик выборки позволяют получать выводы о параметрах генеральной совокупности. Гипотеза (hypothesis) – предположение относительно параметров генеральной совокупности, которое подлежит проверке на основе анализа выборки.

Два типа данных Дискретные данные (discrete data) – представляют собой отдельные значения признака, общее Два типа данных Дискретные данные (discrete data) – представляют собой отдельные значения признака, общее число которых конечно либо если бесконечно, то является счётным, т. е. может быть подсчитано натуральными числами от одного до бесконечности. Непрерывные данные (continuous data) – могут принимать любое значение в некотором интервале.

Критерии измерений Надёжность измерения (reliability) – означает возможность получить воспроизводимые результаты при повторных измерениях Критерии измерений Надёжность измерения (reliability) – означает возможность получить воспроизводимые результаты при повторных измерениях характеристик объекта. Достоверность измерения (exhaustive) – означает соответствие между результатами измерения и его целями, между выбранной шкалой и исследуемыми переменными.

Пять типов шкал Номинальная шкала (nominal scale) – состоит из названий, имён или категорий Пять типов шкал Номинальная шкала (nominal scale) – состоит из названий, имён или категорий для сортировки или классификации объектов, явлений по некоторому признаку. Результаты измерений, полученные при помощи номинальной шкалы, не могут быть упорядочены и с ними не могут производиться арифметические операции. Пример: анкета с тремя вариантами ответов- "Да" – "Нет" – "Не знаю".

Порядковая шкала (ordinal scale) – означает, что числа присваиваются объектам, чтобы обозначить относительные позиции Порядковая шкала (ordinal scale) – означает, что числа присваиваются объектам, чтобы обозначить относительные позиции объектов, но не величину различий между ними. Порядковые номера не сообщают о величине различий. Пример: выстраивание нескольких людей по росту и назначение им порядковых номеров.

Интервальная шкала (interval scale) – позволяет находить разницу между двумя величинами. Обладает всеми свойствами Интервальная шкала (interval scale) – позволяет находить разницу между двумя величинами. Обладает всеми свойствами номинальной и порядковой, но она позволяет указать количественное значение измеряемого признака. Недостатком служит отсутствие нуля в качестве точки отсчёта. Интервальная шкала является непрерывной. Номинальные и порядковые шкалы являются дискретными. Непрерывные шкалы позволяют проводить арифметические операции: складывать, вычитать, умножать и делить.

Относительная шкала (ratio scale) – обладает нулём в качестве точки отсчёта, что позволяет ей Относительная шкала (ratio scale) – обладает нулём в качестве точки отсчёта, что позволяет ей иметь все свойства интервальной шкалы. Для данных этой шкалы справедливы все операции, включая вычитание и деление. Пример: количество лейкоцитов увеличилось в 1, 5 раза. Цена в ноль рублей означает, что товар бесплатный.

Интервальные и относительные шкалы называются числовыми. Они работают с непрерывными данными. Номинальные и порядковые Интервальные и относительные шкалы называются числовыми. Они работают с непрерывными данными. Номинальные и порядковые шкалы работают с дискретными данными.

Дихотомическая шкала (dichotomous scale) – номинальная шкала, которая состоит из двух категорий. Пример: дихотомической Дихотомическая шкала (dichotomous scale) – номинальная шкала, которая состоит из двух категорий. Пример: дихотомической шкалой измеряется пол человека. Вопрос с двумя вариантами ответа (Да=1, Нет=0) также представляет собой пример дихотомической шкалы. Пациент «здоров» - «болен» . Отек "есть" - "нет".

Обсуждены пять типов шкал • Номинальные шкалы позволяют описывать наблюдения в терминах качественных признаков. Обсуждены пять типов шкал • Номинальные шкалы позволяют описывать наблюдения в терминах качественных признаков. • Порядковые шкалы позволяют упорядочивать наблюдаемые объекты от меньшего к большему

• Номинальные и порядковые шкалы являются дискретными. • Интервальные шкалы состоят из интервалов • Номинальные и порядковые шкалы являются дискретными. • Интервальные шкалы состоят из интервалов равного размера, которые позволяют определить количественное значение наблюдаемого признака. • Относительная шкала обладает нулём в качестве точки отсчёта, что позволяет ей иметь все свойства интервальной шкалы. Для данных этой шкалы справедливы все операции, включая вычитание и деление.

• Дихотомические шкалы – это номинальные шкалы, с которыми можно поступать так же, • Дихотомические шкалы – это номинальные шкалы, с которыми можно поступать так же, как с интервальными.

Кумулятивная вероятность Определение. Кумулятивная вероятность выживания (Cumulative Probability of surviving) в момент времени t Кумулятивная вероятность Определение. Кумулятивная вероятность выживания (Cumulative Probability of surviving) в момент времени t – это то же самое, что доля выживших пациентов к этому моменту времени. Пример. Если говорится, что кумулятивная вероятность выживания после проведения пятилетнего курса лечения равна 0. 7, то это значит, что из рассматриваемой группы пациентов в живых осталось 70% от начального количества, а 30% умерло. Другими словами, из каждой сотни человек 30 умерло в течение первых 5 лет.

Зависимые и независимые выборки Определение. Независимые выборки, в которые объекты исследования набирались независимо друг Зависимые и независимые выборки Определение. Независимые выборки, в которые объекты исследования набирались независимо друг от друга. Альтернатива независимым выборкам – зависимые (связные, парные) выборки.

Гипотеза Двусторонняя и односторонняя гипотезы Определение. Гипотеза называется двусторонней (2 -sided), если она состоит Гипотеза Двусторонняя и односторонняя гипотезы Определение. Гипотеза называется двусторонней (2 -sided), если она состоит в равенстве двух величин. Пример двусторонней гипотезы: A=T. Определение. Гипотеза называется односторонней (1 -sided), если она состоит в неравенстве двух величин: А> T или A

Ошибка первого рода — например, анализ крови показал наличие заболевания, хотя на самом деле Ошибка первого рода — например, анализ крови показал наличие заболевания, хотя на самом деле человек здоров. Ошибка второго рода — человек болен, но анализ крови этого не показал

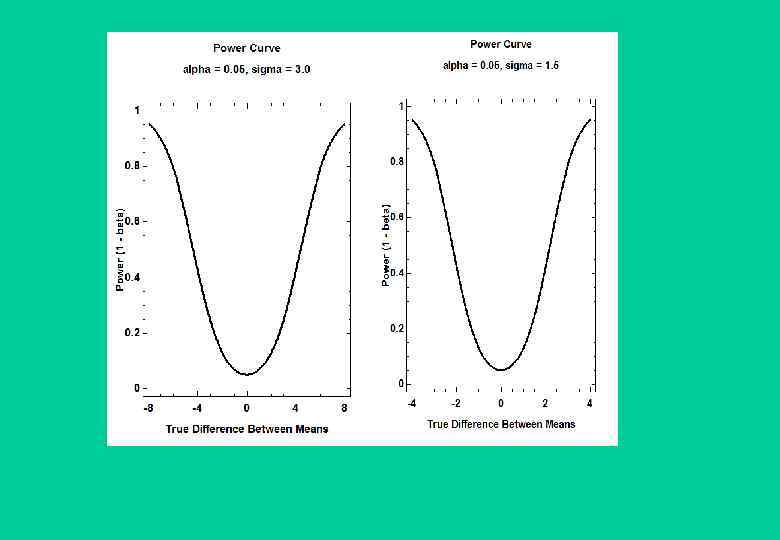
Вероятности ошибок (уровень значимости и мощность) Вероятность ошибки первого рода при проверке статистических гипотез Вероятности ошибок (уровень значимости и мощность) Вероятность ошибки первого рода при проверке статистических гипотез называют уровнем значимости Вероятность ошибки второго рода не имеет какогото особого общепринятого названия, на письме обозначается греческой буквой β. Однако с этой величиной тесно связана другая, имеющая большое статистическое значение — мощность критерия. Она вычисляется по формуле (1 - β). Таким образом, чем выше мощность, тем меньше вероятность совершить ошибку второго рода.

Доверительный интервал Определение. Доверительный интервал (confidence interval) для некоторой величины - это диапазон в Доверительный интервал Определение. Доверительный интервал (confidence interval) для некоторой величины - это диапазон в котором находится истинное значение этой величины (с определенным уровнем доверия). Пример. Пусть исследуемой величиной является количество пациентов в год. В среднем их количество равно 500, а 95% -доверительный интервал – (350, 900). Это означает, что, скорее всего (с вероятностью 95%), в течение года в клинику обратятся не менее 350 и не более 900 человек. Обозначение. Очень часто используются сокращение: ДИ 95 % (CI 95%) – это доверительный интервал с уровнем доверия 95%.

МЕТОДЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ 1 ОПИСАТЕЛЬНАЯ СТАТИСТИКА мера положения мера рассеивания мера формы ПРОВЕРКА СТАТИСТИЧЕСКИХ МЕТОДЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ 1 ОПИСАТЕЛЬНАЯ СТАТИСТИКА мера положения мера рассеивания мера формы ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ Параметрические критерии Непараметрические критерии 2. МНОГОМЕРНЫЕ МЕТОДЫ Кластерный анализ Факторный анализ Метод главных компонент Дискриминантный анализ Многомерное шкалирование Распознавание образов Нейронные сети и т. д. 3. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ

Построение оценочных алгоритмов 1. Средние арифметические значения всех признаков отдельно для каждой выборки, в Построение оценочных алгоритмов 1. Средние арифметические значения всех признаков отдельно для каждой выборки, в результате получим векторы R 1 и R 2. 2. Сумму смешанных произведений СП – матрицы V 1 и V 2 для каждой выборки, где каждый элемент подсчитывается по формуле, для матрицы V 1: N Vik = ( Xim + Xi (1) ) ( Xkm + Xk (2) ), m а матрицы V 2 по формуле:

N 1 + N 2 Vik = ( Xim + Xi (2) ) ( N 1 + N 2 Vik = ( Xim + Xi (2) ) ( Xkm + Xk (2) ). m=N 1 + 1 3. Обобщенную СП-матрицу V=V 1+V 2 , где поэлементно сложение ведётся 4. Вычисляют матрицу V-1. 5. Матрицу W-1 , где W-1 = (N 1 + N 2 - 2) V-1. 6. Вектор разностей средних арифметических значений: = R 1 – R 2. 7. Коэффициенты дискриминантной функции: W = W-1. 8. Расстояние Махаланобиса: D 12 = W T.

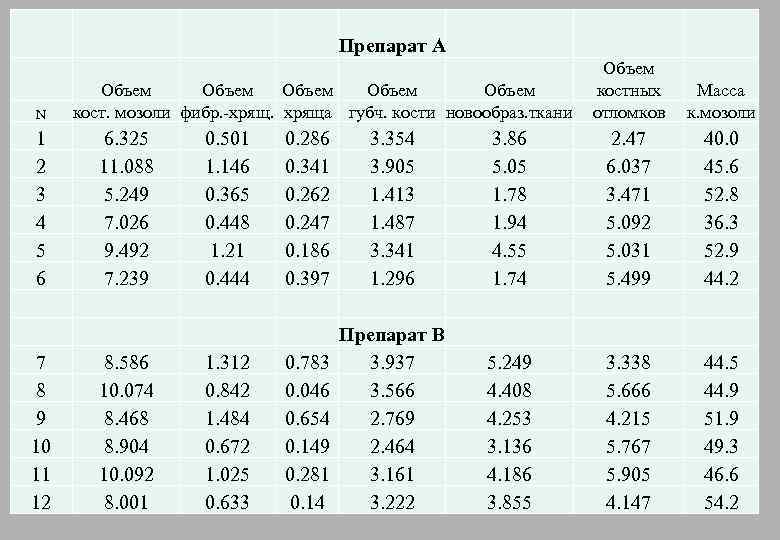Препарат А N 1 2 3 4 5 6 7 8 9 10 11 Препарат А N 1 2 3 4 5 6 7 8 9 10 11 12 Объем Объем кост. мозоли фибр. -хряща губч. кости новообраз. ткани 6. 325 11. 088 5. 249 7. 026 9. 492 7. 239 8. 586 10. 074 8. 468 8. 904 10. 092 8. 001 0. 501 1. 146 0. 365 0. 448 1. 21 0. 444 1. 312 0. 842 1. 484 0. 672 1. 025 0. 633 Объем костных отломков Масса к. мозоли 0. 286 0. 341 0. 262 0. 247 0. 186 0. 397 3. 354 3. 905 1. 413 1. 487 3. 341 1. 296 3. 86 5. 05 1. 78 1. 94 4. 55 1. 74 2. 47 6. 037 3. 471 5. 092 5. 031 5. 499 40. 0 45. 6 52. 8 36. 3 52. 9 44. 2 0. 783 0. 046 0. 654 0. 149 0. 281 0. 14 Препарат B 3. 937 3. 566 2. 769 2. 464 3. 161 3. 222 5. 249 4. 408 4. 253 3. 136 4. 186 3. 855 3. 338 5. 666 4. 215 5. 767 5. 905 4. 147 44. 5 44. 9 51. 9 49. 3 46. 6 54. 2

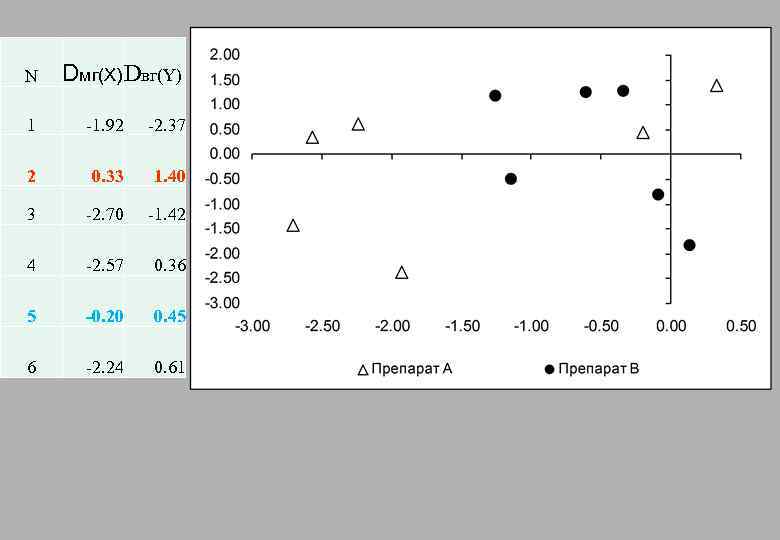N Dмг(X) Dвг(Y) 1 -1. 92 -2. 37 2 0. 33 1. 40 3 N Dмг(X) Dвг(Y) 1 -1. 92 -2. 37 2 0. 33 1. 40 3 -2. 70 -1. 42 4 -2. 57 0. 36 5 -0. 20 0. 45 6 -2. 24 0. 61

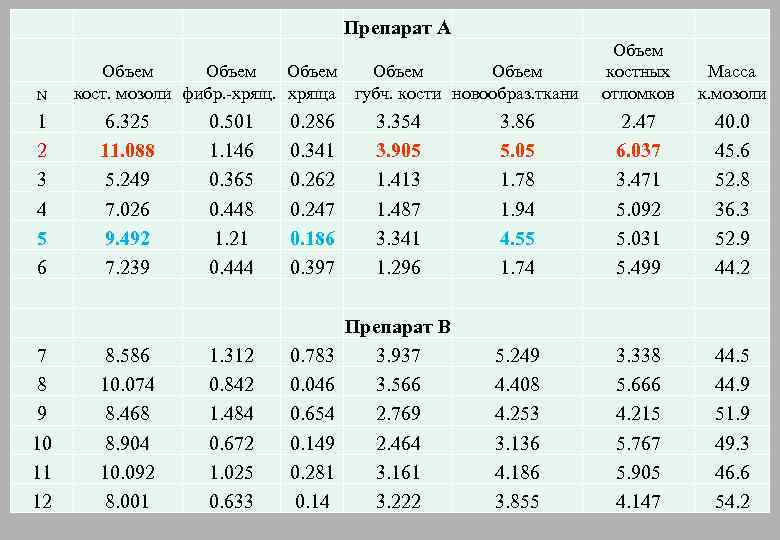Препарат А N 1 2 3 4 5 6 7 8 9 10 11 Препарат А N 1 2 3 4 5 6 7 8 9 10 11 12 Объем Объем кост. мозоли фибр. -хряща губч. кости новообраз. ткани 6. 325 11. 088 5. 249 7. 026 9. 492 7. 239 8. 586 10. 074 8. 468 8. 904 10. 092 8. 001 0. 501 1. 146 0. 365 0. 448 1. 21 0. 444 1. 312 0. 842 1. 484 0. 672 1. 025 0. 633 Объем костных отломков Масса к. мозоли 0. 286 0. 341 0. 262 0. 247 0. 186 0. 397 3. 354 3. 905 1. 413 1. 487 3. 341 1. 296 3. 86 5. 05 1. 78 1. 94 4. 55 1. 74 2. 47 6. 037 3. 471 5. 092 5. 031 5. 499 40. 0 45. 6 52. 8 36. 3 52. 9 44. 2 0. 783 0. 046 0. 654 0. 149 0. 281 0. 14 Препарат B 3. 937 3. 566 2. 769 2. 464 3. 161 3. 222 5. 249 4. 408 4. 253 3. 136 4. 186 3. 855 3. 338 5. 666 4. 215 5. 767 5. 905 4. 147 44. 5 44. 9 51. 9 49. 3 46. 6 54. 2

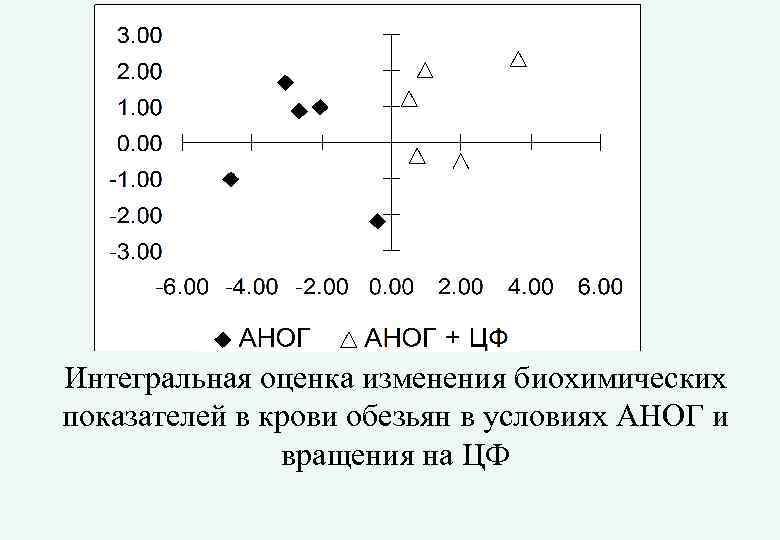Интегральная оценка изменения биохимических показателей в крови обезьян в условиях АНОГ и вращения на 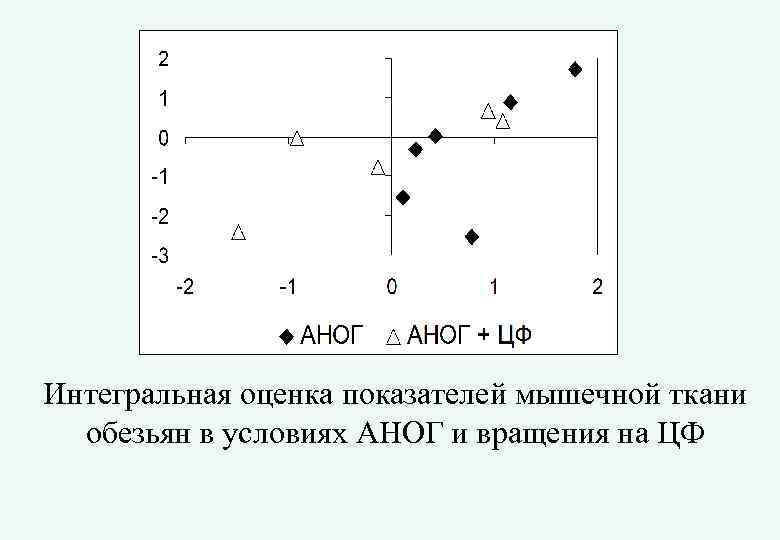Интегральная оценка изменения биохимических показателей в крови обезьян в условиях АНОГ и вращения на ЦФ

Интегральная оценка показателей мышечной ткани обезьян в условиях АНОГ и вращения на ЦФ Интегральная оценка показателей мышечной ткани обезьян в условиях АНОГ и вращения на ЦФ

Интегральная оценка морфологических показателей костной ткани обезьян в условиях АНОГ и вращения на ЦФ 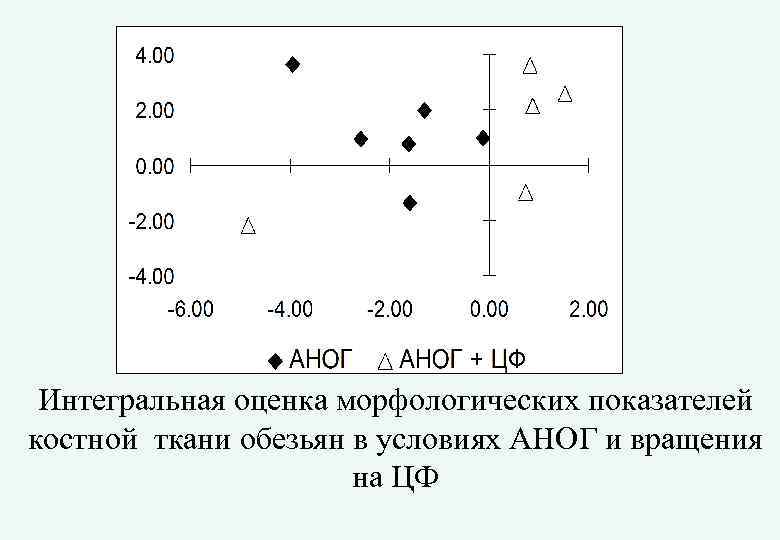Интегральная оценка морфологических показателей костной ткани обезьян в условиях АНОГ и вращения на ЦФ

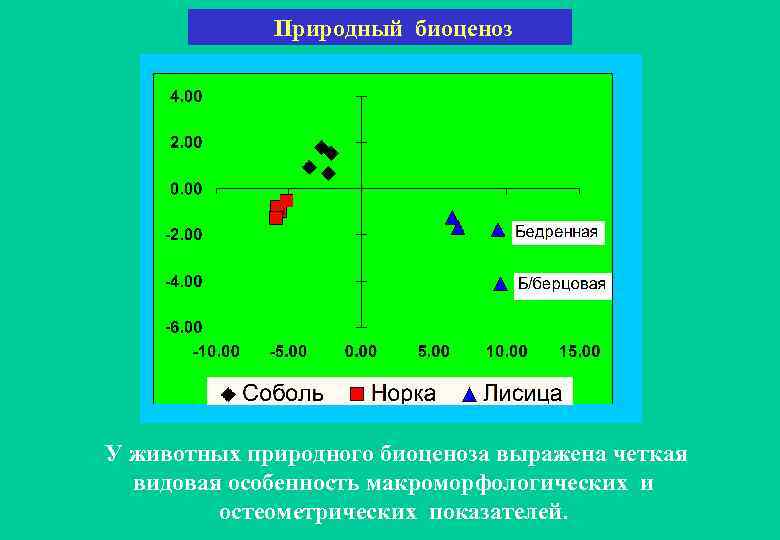Природный биоценоз У животных природного биоценоза выражена четкая видовая особенность макроморфологических и остеометрических Природный биоценоз У животных природного биоценоза выражена четкая видовая особенность макроморфологических и остеометрических показателей.

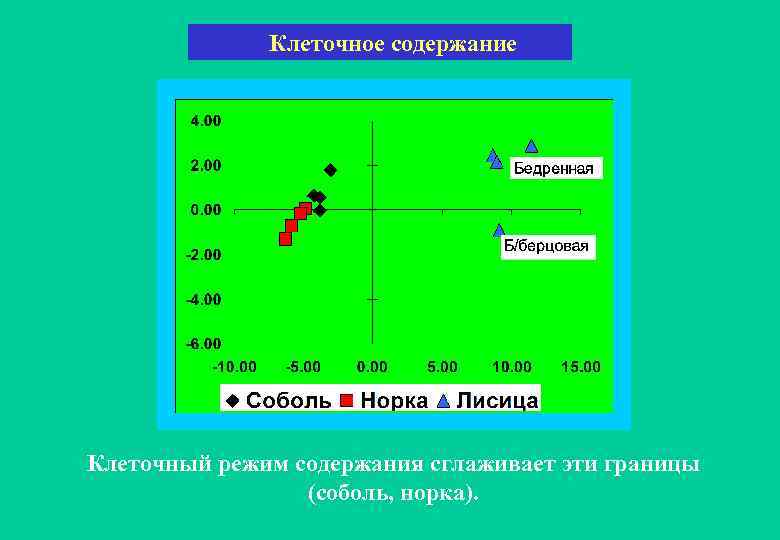Клеточное содержание Клеточный режим содержания сглаживает эти границы (соболь, норка). Клеточное содержание Клеточный режим содержания сглаживает эти границы (соболь, норка).

Применение дискриминантного анализа для диагностики стадий артериальной гипертензии Было исследовано 220 пациентов с различными Применение дискриминантного анализа для диагностики стадий артериальной гипертензии Было исследовано 220 пациентов с различными стадиями АГ. Все пациенты были разделены на 3 группы: - 1 -я группа – 74 пациентов с АГ I стадии; - 2 -я группа – 74 пациентов с АГ II стадии; -3 -я группа – 72 пациентов с АГ III стадии. Для определения значимых для формирования диагноза признаков были проанализированы 1. антропометрические показатели (рост, вес, индекс массы тела, окружность талии, окружность бедер, индекс талия/бедро); 2. гемодинамические (уровни систолического, диастолического и пульсового давления, частота сердечных сокращений); 3. клиниколабораторные показатели углеводного обмена (уровень глюкозы, инсулина, гликированого гемоглобина с математическим расчетом индексов инсулинорезистентности HOMA, Caro, Duncan;

4. показатели углеводного спектра (общий холестерин, триглецириды, холестерин липопротеидов высокой, низкой и очень низкой 4. показатели углеводного спектра (общий холестерин, триглецириды, холестерин липопротеидов высокой, низкой и очень низкой плотности, коэффициент атерогенности, аполипопротеин B 100); 5. показатели активности адипокиновой системы (интерлейкин-6, фактор некроза опухолей-α, адипонектин, ингибитор активатора плазминогена-1). ИТОГО: около 27 показателей

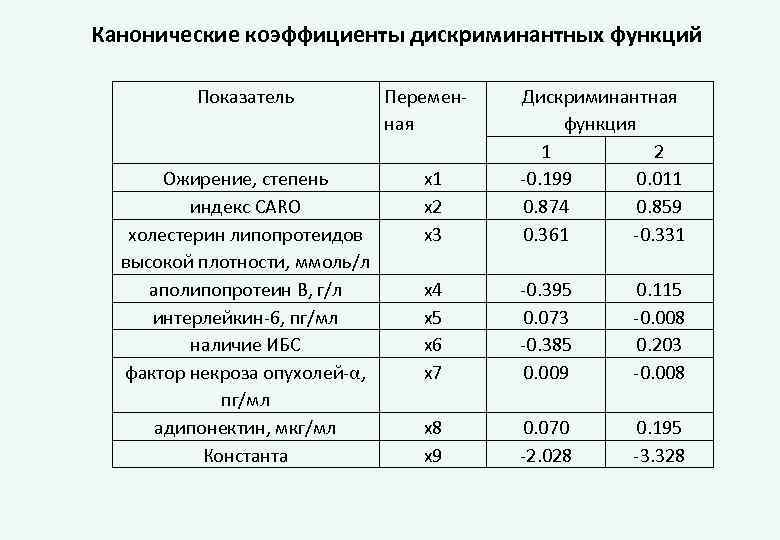Канонические коэффициенты дискриминантных функций Показатель Ожирение, степень индекс CARO холестерин липопротеидов высокой плотности, ммоль/л Канонические коэффициенты дискриминантных функций Показатель Ожирение, степень индекс CARO холестерин липопротеидов высокой плотности, ммоль/л аполипопротеин B, г/л интерлейкин-6, пг/мл наличие ИБС фактор некроза опухолей-α, пг/мл адипонектин, мкг/мл Константа Переменная x 1 x 2 x 3 Дискриминантная функция 1 2 -0. 199 0. 011 0. 874 0. 859 0. 361 -0. 331 x 4 x 5 x 6 x 7 -0. 395 0. 073 -0. 385 0. 009 0. 115 -0. 008 0. 203 -0. 008 x 9 0. 070 -2. 028 0. 195 -3. 328

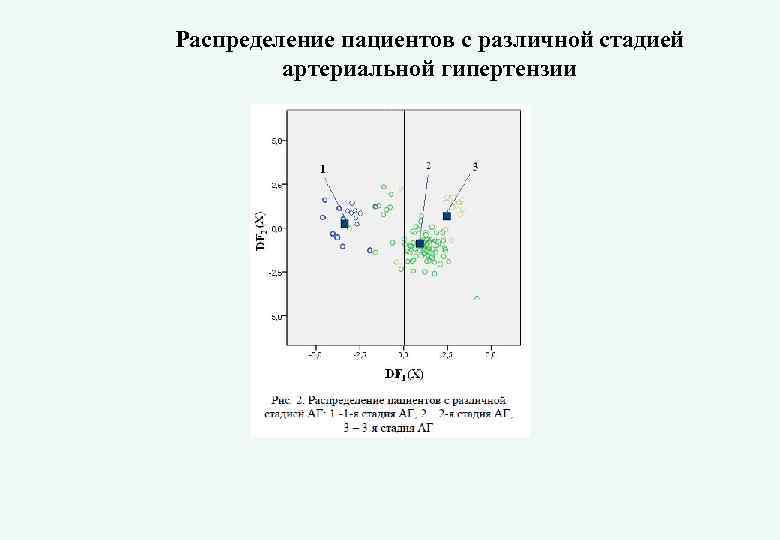Распределение пациентов с различной стадией артериальной гипертензии Распределение пациентов с различной стадией артериальной гипертензии

Распределение пациентов с различной стадией артериальной гипертензии 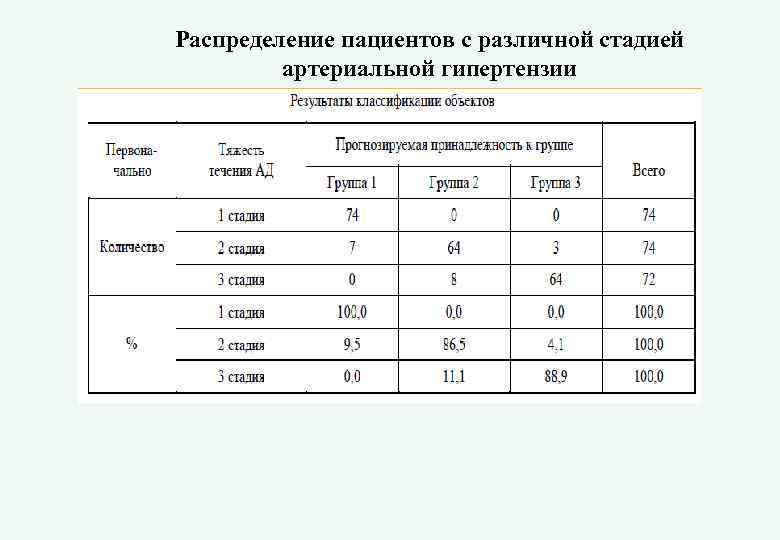Распределение пациентов с различной стадией артериальной гипертензии

Методы кластерного анализа Методы кластерного анализа

Метод главных компонент Метод главных компонент