Случайные величины.ppt
- Количество слайдов: 37
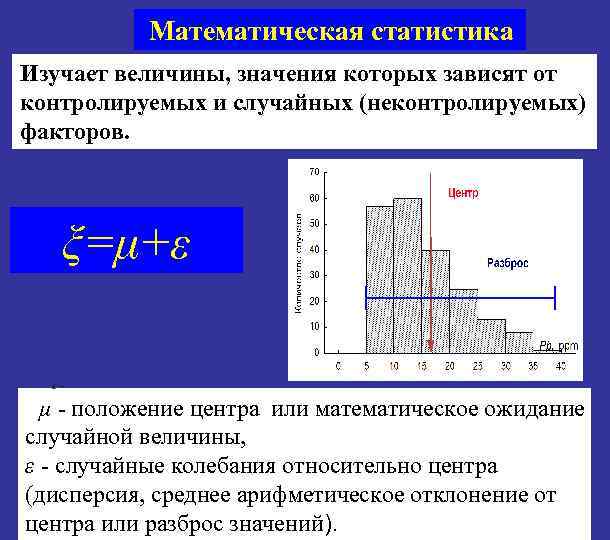 Математическая статистика Изучает величины, значения которых зависят от контролируемых и случайных (неконтролируемых) факторов. ξ=μ+ε μ - положение центра или математическое ожидание случайной величины, ε - случайные колебания относительно центра (дисперсия, среднее арифметическое отклонение от центра или разброс значений).
Математическая статистика Изучает величины, значения которых зависят от контролируемых и случайных (неконтролируемых) факторов. ξ=μ+ε μ - положение центра или математическое ожидание случайной величины, ε - случайные колебания относительно центра (дисперсия, среднее арифметическое отклонение от центра или разброс значений).
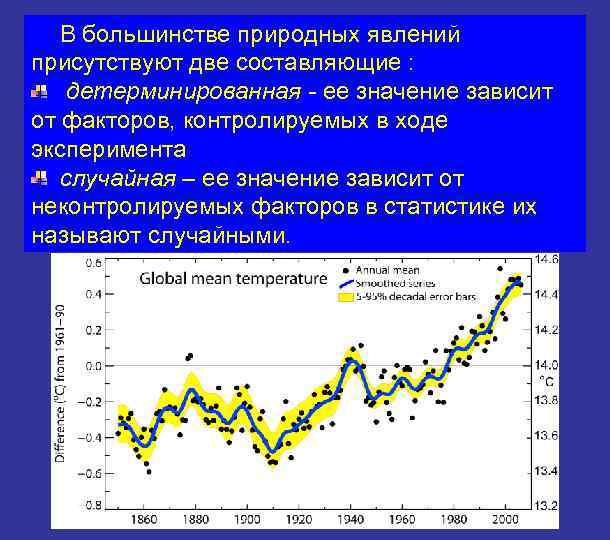 В большинстве природных явлений присутствуют две составляющие : детерминированная - ее значение зависит от факторов, контролируемых в ходе эксперимента случайная – ее значение зависит от неконтролируемых факторов в статистике их называют случайными.
В большинстве природных явлений присутствуют две составляющие : детерминированная - ее значение зависит от факторов, контролируемых в ходе эксперимента случайная – ее значение зависит от неконтролируемых факторов в статистике их называют случайными.
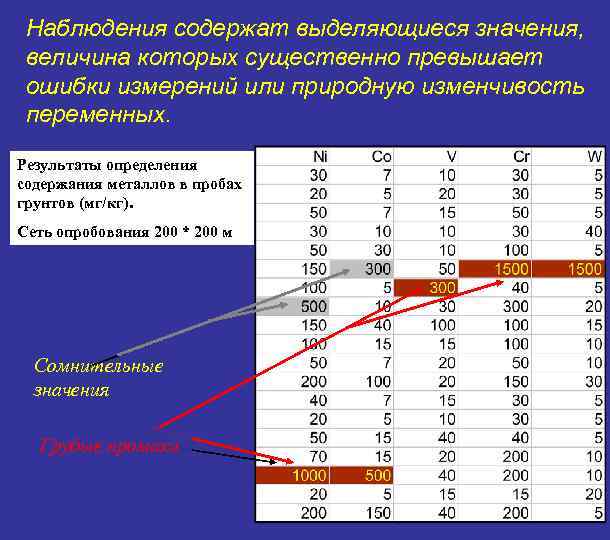 Наблюдения содержат выделяющиеся значения, величина которых существенно превышает ошибки измерений или природную изменчивость переменных. Результаты определения содержания металлов в пробах грунтов (мг/кг). Сеть опробования 200 * 200 м Сомнительные значения Грубые промахи ? ?
Наблюдения содержат выделяющиеся значения, величина которых существенно превышает ошибки измерений или природную изменчивость переменных. Результаты определения содержания металлов в пробах грунтов (мг/кг). Сеть опробования 200 * 200 м Сомнительные значения Грубые промахи ? ?
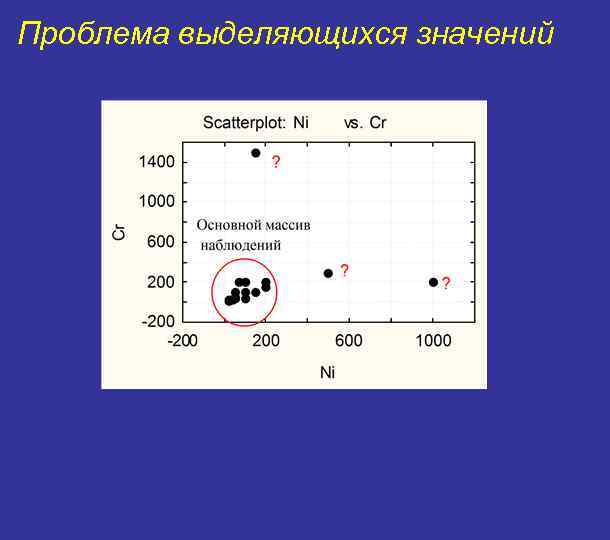 Проблема выделяющихся значений
Проблема выделяющихся значений
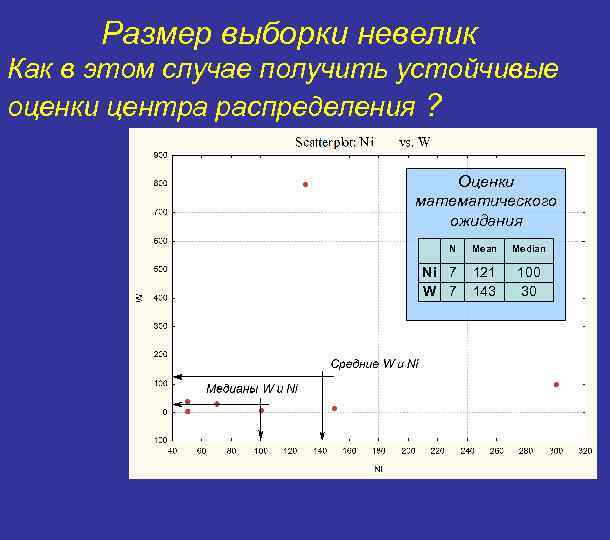 Размер выборки невелик Как в этом случае получить устойчивые оценки центра распределения ? Оценки математического ожидания N Mean Median Ni 7 W 7 121 143 100 30
Размер выборки невелик Как в этом случае получить устойчивые оценки центра распределения ? Оценки математического ожидания N Mean Median Ni 7 W 7 121 143 100 30
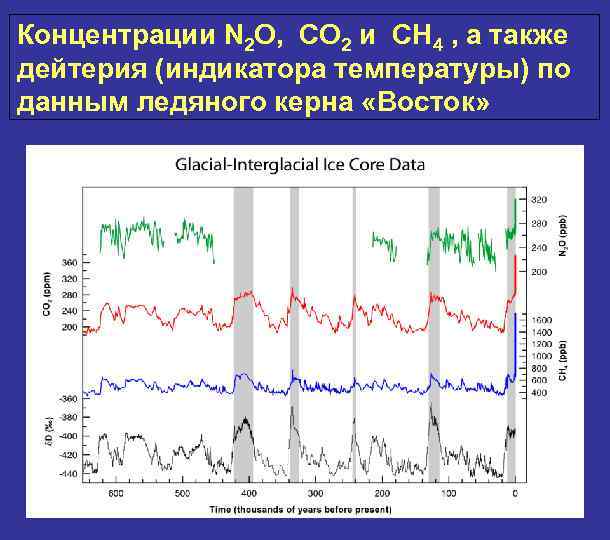 Концентрации N 2 O, CO 2 и CH 4 , а также дейтерия (индикатора температуры) по данным ледяного керна «Восток»
Концентрации N 2 O, CO 2 и CH 4 , а также дейтерия (индикатора температуры) по данным ледяного керна «Восток»
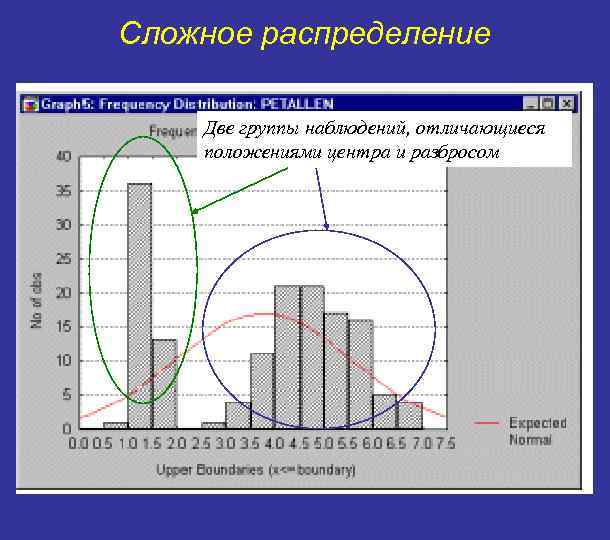 Сложное распределение Две группы наблюдений, отличающиеся положениями центра и разбросом
Сложное распределение Две группы наблюдений, отличающиеся положениями центра и разбросом
 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ В большинстве явлений присутствуют и детерминированная, и случайная составляющая, Основная задача - выделить закономерности на фоне случайных изменений. События и их вероятности Событие -- это всякий факт, который может произойти или не произойти в результате опыта. Вероятность p(А) есть численная мера возможности события А Для невозможного события p(А) = 0. Для достоверного события p(А) = 1 Измерения вероятности n(A)/N→p(A ), если N→∞
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ В большинстве явлений присутствуют и детерминированная, и случайная составляющая, Основная задача - выделить закономерности на фоне случайных изменений. События и их вероятности Событие -- это всякий факт, который может произойти или не произойти в результате опыта. Вероятность p(А) есть численная мера возможности события А Для невозможного события p(А) = 0. Для достоверного события p(А) = 1 Измерения вероятности n(A)/N→p(A ), если N→∞
 Типы случайных величин Выделяют два типа случайных величин: дискретные - принимают только определенные значения (численность населения); непрерывные – принимают любые вещественные значения (содержание химических элементов). Генеральная совокупностью и выборка Множество возможных значений случайных величин называют генеральной совокупностью. Часть генеральной совокупности называют выборкой. Оценки положения центра и разброса значений случайной величины по выборке и генеральной совокупности, как правило, отличаются. Сформировать представительную выборку непросто. При отсутствии информации о совокупности наилучшим вариантом является случайный выбор.
Типы случайных величин Выделяют два типа случайных величин: дискретные - принимают только определенные значения (численность населения); непрерывные – принимают любые вещественные значения (содержание химических элементов). Генеральная совокупностью и выборка Множество возможных значений случайных величин называют генеральной совокупностью. Часть генеральной совокупности называют выборкой. Оценки положения центра и разброса значений случайной величины по выборке и генеральной совокупности, как правило, отличаются. Сформировать представительную выборку непросто. При отсутствии информации о совокупности наилучшим вариантом является случайный выбор.
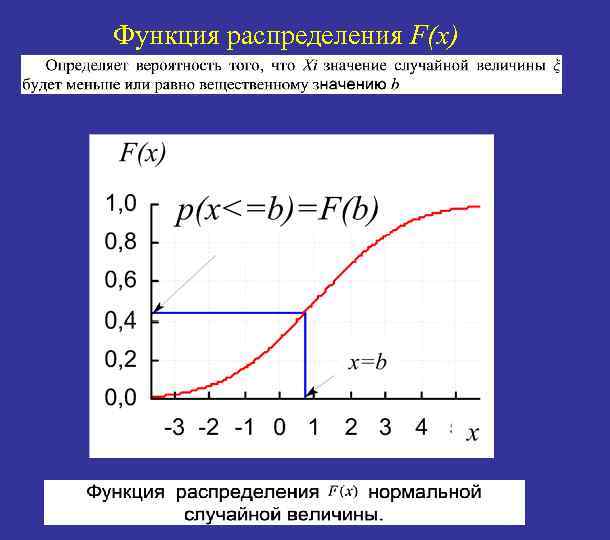 Функция распределения F(x)
Функция распределения F(x)
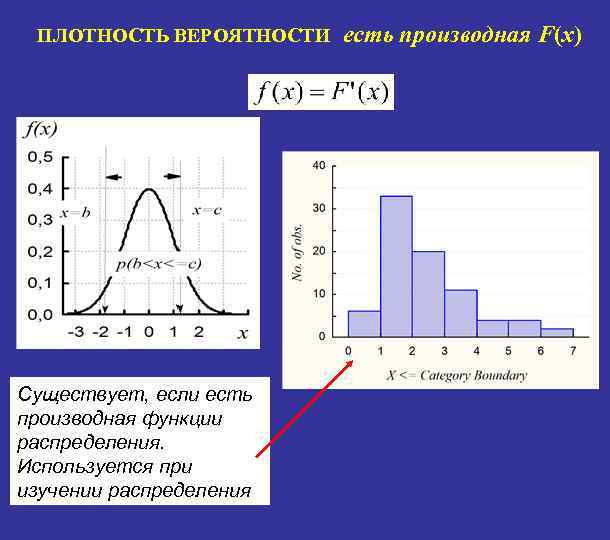 ПЛОТНОСТЬ ВЕРОЯТНОСТИ Существует, если есть производная функции распределения. Используется при изучении распределения есть производная F(x)
ПЛОТНОСТЬ ВЕРОЯТНОСТИ Существует, если есть производная функции распределения. Используется при изучении распределения есть производная F(x)
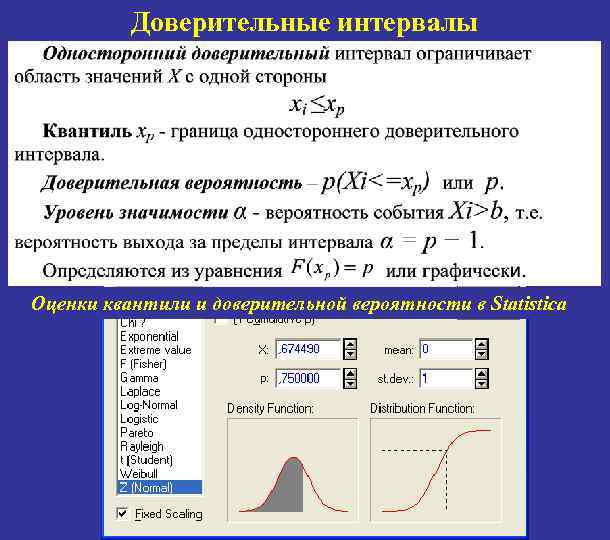 Доверительные интервалы Оценки квантили и доверительной вероятности в Statistica
Доверительные интервалы Оценки квантили и доверительной вероятности в Statistica
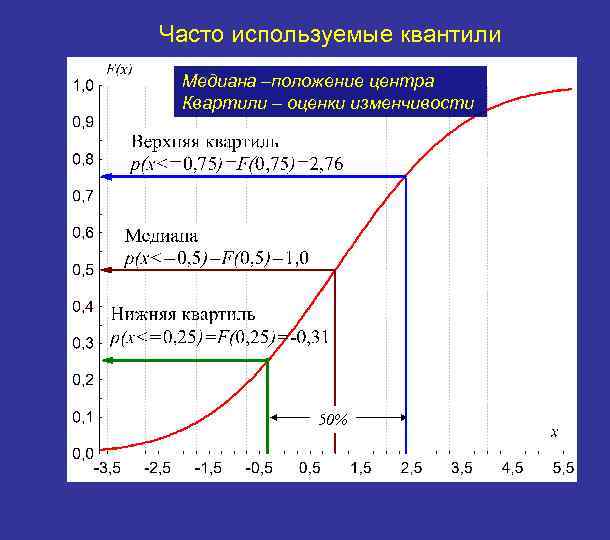 Часто используемые квантили Медиана –положение центра Квартили – оценки изменчивости 50%
Часто используемые квантили Медиана –положение центра Квартили – оценки изменчивости 50%
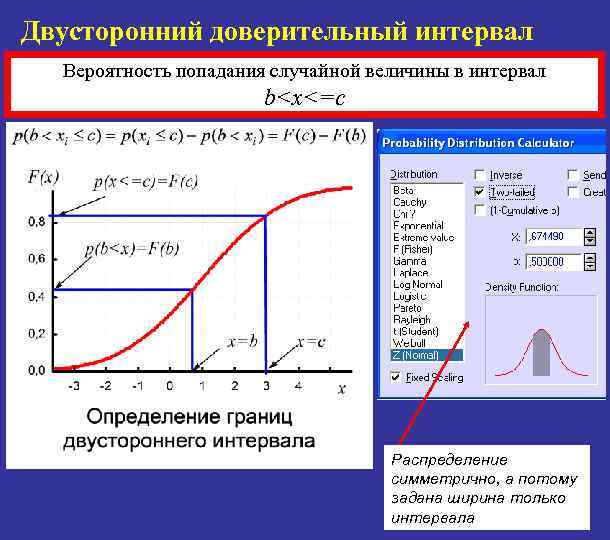 Двусторонний доверительный интервал Вероятность попадания случайной величины в интервал b
Двусторонний доверительный интервал Вероятность попадания случайной величины в интервал b
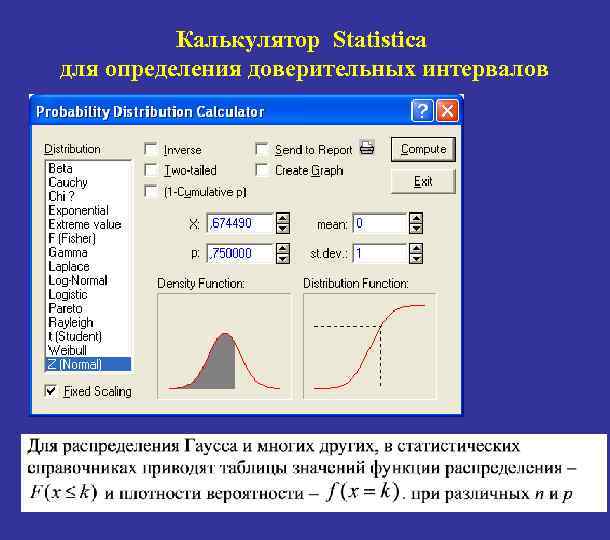 Калькулятор Statistica для определения доверительных интервалов
Калькулятор Statistica для определения доверительных интервалов
 Варианты записи наблюдений Результаты измерений параметра В порядке поступления 24, 8 32, 5 20, 1 19, 6 Вариационный ряд 19, 6 20, 1 24, 8 32, 5 Ранги наблюдений 1 2, 5 4 5 Формат записи Результат вычислений запасов металла - 11476577 т Выбор шкалы: ~ 11, 476577 млн т. Отбрасывание «лишних» знаков и округление (до четного): ~11, 5 млн т или ~12 млн т.
Варианты записи наблюдений Результаты измерений параметра В порядке поступления 24, 8 32, 5 20, 1 19, 6 Вариационный ряд 19, 6 20, 1 24, 8 32, 5 Ранги наблюдений 1 2, 5 4 5 Формат записи Результат вычислений запасов металла - 11476577 т Выбор шкалы: ~ 11, 476577 млн т. Отбрасывание «лишних» знаков и округление (до четного): ~11, 5 млн т или ~12 млн т.
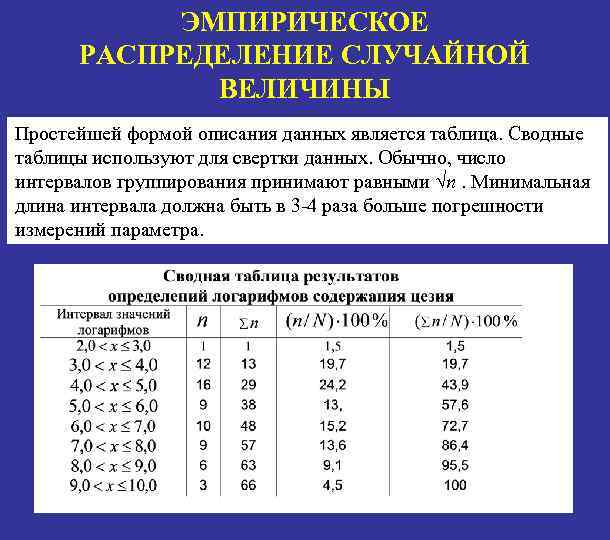 ЭМПИРИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ СЛУЧАЙНОЙ ВЕЛИЧИНЫ Простейшей формой описания данных является таблица. Сводные таблицы используют для свертки данных. Обычно, число интервалов группирования принимают равными √n. Минимальная длина интервала должна быть в 3 -4 раза больше погрешности измерений параметра.
ЭМПИРИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ СЛУЧАЙНОЙ ВЕЛИЧИНЫ Простейшей формой описания данных является таблица. Сводные таблицы используют для свертки данных. Обычно, число интервалов группирования принимают равными √n. Минимальная длина интервала должна быть в 3 -4 раза больше погрешности измерений параметра.
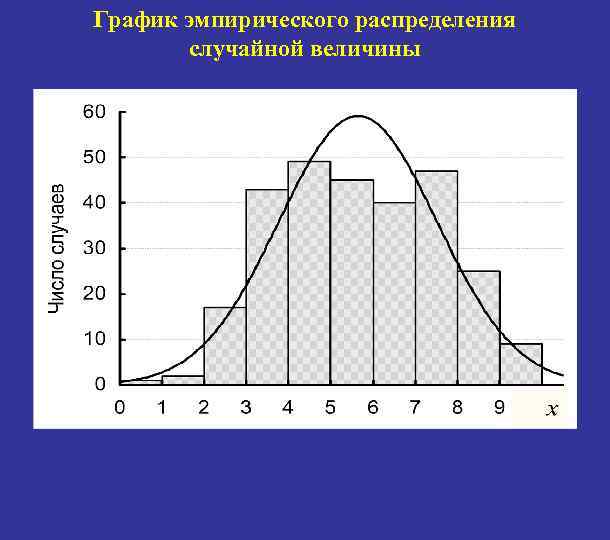 График эмпирического распределения случайной величины
График эмпирического распределения случайной величины
 ТЕОРЕТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ Часто используют распределения: нормальное, логнормальное, биномиальное, Пуассона, Стьюдента, 2 - квадрат и Фишера. Нормальное распределение или распределение Гаусса f(x)=exp[(x−μ)/2σ]2 / (σ√ 2π∙) Функция двух параметров: математического ожидания - μ стандартного отклонения - σ
ТЕОРЕТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ Часто используют распределения: нормальное, логнормальное, биномиальное, Пуассона, Стьюдента, 2 - квадрат и Фишера. Нормальное распределение или распределение Гаусса f(x)=exp[(x−μ)/2σ]2 / (σ√ 2π∙) Функция двух параметров: математического ожидания - μ стандартного отклонения - σ
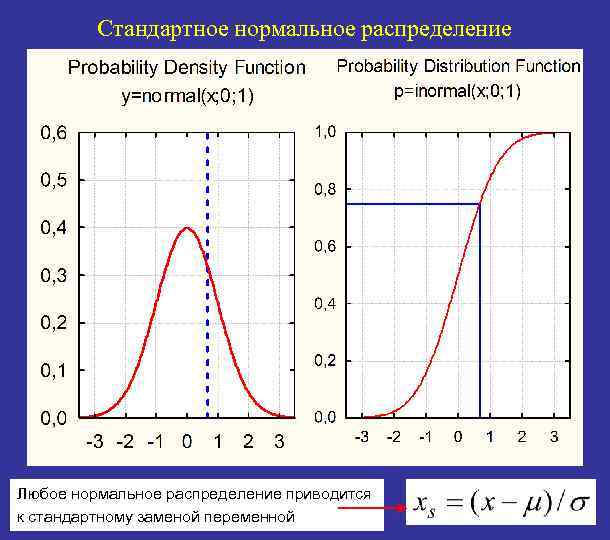 Стандартное нормальное распределение Любое нормальное распределение приводится к стандартному заменой переменной
Стандартное нормальное распределение Любое нормальное распределение приводится к стандартному заменой переменной
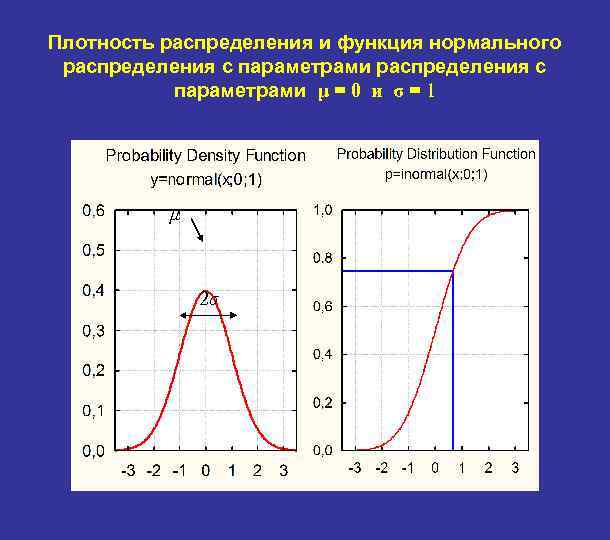 Плотность распределения и функция нормального распределения с параметрами μ = 0 и σ = 1 μ 2σ
Плотность распределения и функция нормального распределения с параметрами μ = 0 и σ = 1 μ 2σ
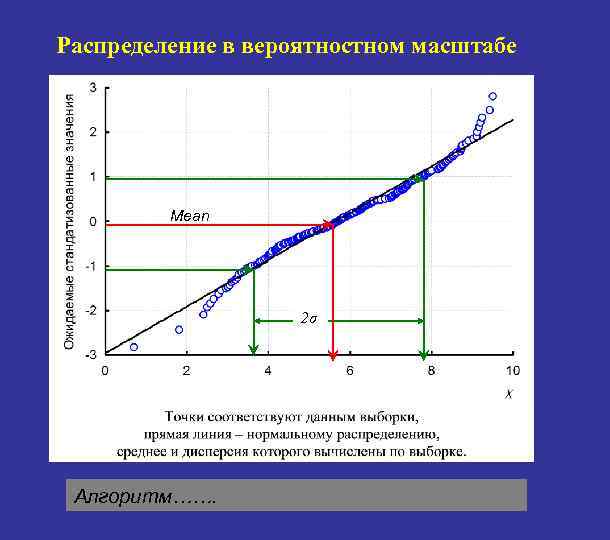 Распределение в вероятностном масштабе Mean 2σ Алгоритм…….
Распределение в вероятностном масштабе Mean 2σ Алгоритм…….
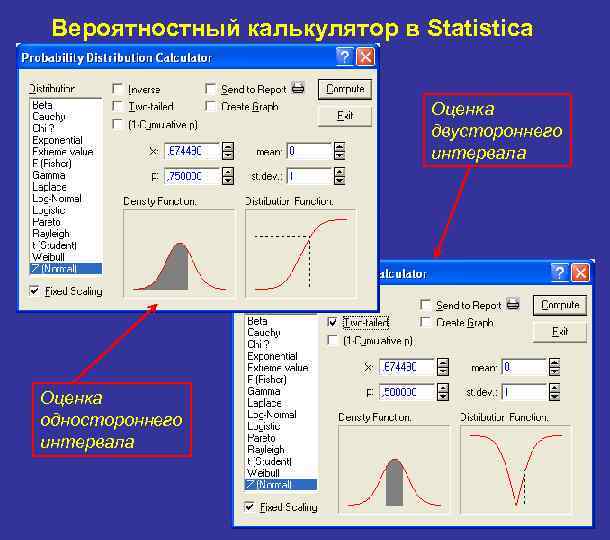 Вероятностный калькулятор в Statistica Оценка двустороннего интервала Оценка одностороннего интервала
Вероятностный калькулятор в Statistica Оценка двустороннего интервала Оценка одностороннего интервала
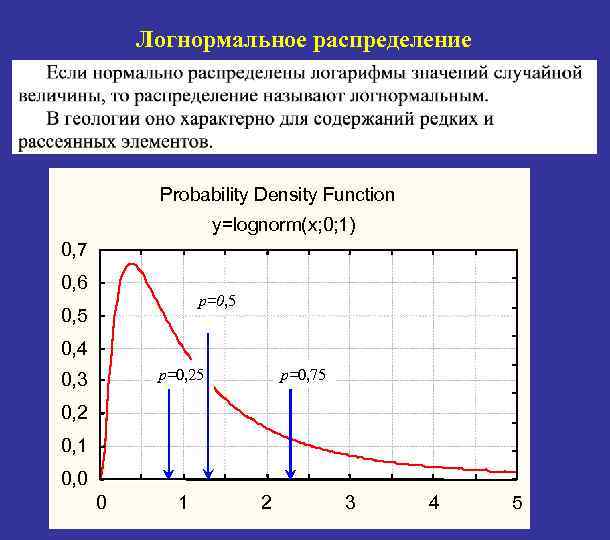 Логнормальное распределение Probability Density Function y=lognorm(x; 0; 1) 0, 7 0, 6 р=0, 5 0, 4 р=0, 25 0, 3 р=0, 75 0, 2 0, 1 0, 0 0 1 2 3 4 5
Логнормальное распределение Probability Density Function y=lognorm(x; 0; 1) 0, 7 0, 6 р=0, 5 0, 4 р=0, 25 0, 3 р=0, 75 0, 2 0, 1 0, 0 0 1 2 3 4 5
 Распределение Пуассона Плотность вероятности распределения Пуассона
Распределение Пуассона Плотность вероятности распределения Пуассона
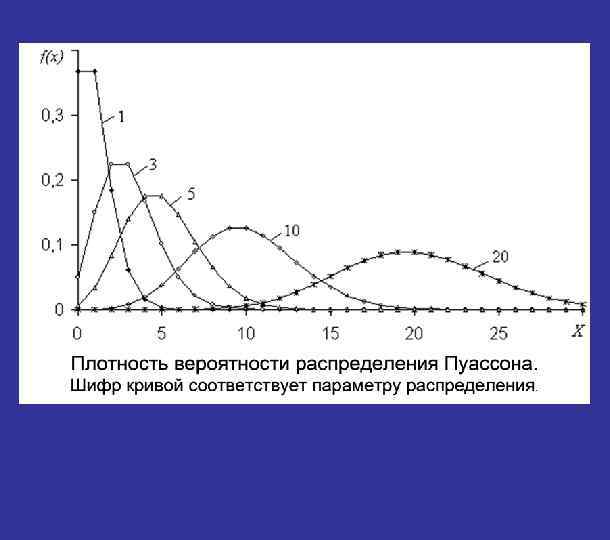
 РАСПРЕДЕЛЕНИЯ, СВЯЗАННЫЕ С НОРМАЛЬНЫМ
РАСПРЕДЕЛЕНИЯ, СВЯЗАННЫЕ С НОРМАЛЬНЫМ
 Распределение Стьюдента Аналитическое описание распределения не приводится из -за сложности формулы. Здесь важно , что оно описывает распределение переменной t, которая равна где x – случайная величина, имеющая нормальное распределение с параметрами x 0= μ=0 и σ=1; ν - число степеней свободы; n – число наблюдений x, которые участвовали в расчетах величины t. Если μ≠ 0 и σ≠ 1, делают замену переменных Число степеней свободы определяется количеством независимых переменных в выборке, по которой вычисляли значение t: ν = n, если μ известно; ν = n – 1, если используют оценку μ*, полученную по выборке. В этом случае n-е измерение является зависимым, так как его можно вычислить, зная μ* xn = nμ*−∑n− 11 xi. .
Распределение Стьюдента Аналитическое описание распределения не приводится из -за сложности формулы. Здесь важно , что оно описывает распределение переменной t, которая равна где x – случайная величина, имеющая нормальное распределение с параметрами x 0= μ=0 и σ=1; ν - число степеней свободы; n – число наблюдений x, которые участвовали в расчетах величины t. Если μ≠ 0 и σ≠ 1, делают замену переменных Число степеней свободы определяется количеством независимых переменных в выборке, по которой вычисляли значение t: ν = n, если μ известно; ν = n – 1, если используют оценку μ*, полученную по выборке. В этом случае n-е измерение является зависимым, так как его можно вычислить, зная μ* xn = nμ*−∑n− 11 xi. .
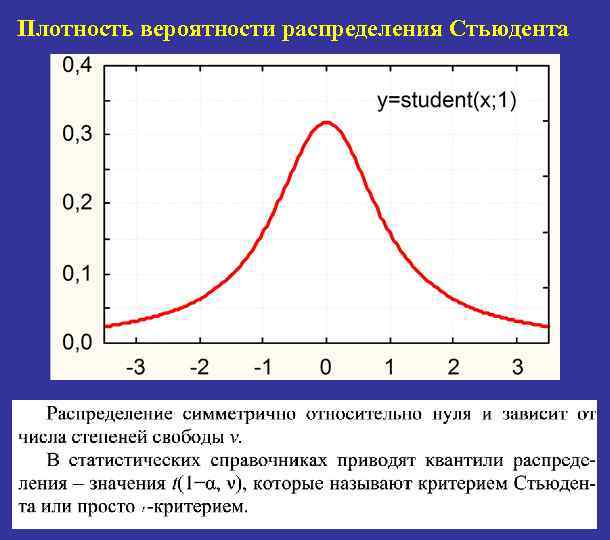 Плотность вероятности распределения Стьюдента
Плотность вероятности распределения Стьюдента
 F–распределение (Фишера) 1 -α/2=0, 25 1 -α/2=0, 75
F–распределение (Фишера) 1 -α/2=0, 25 1 -α/2=0, 75
 Распределение χ2 (хи–квадрат)
Распределение χ2 (хи–квадрат)
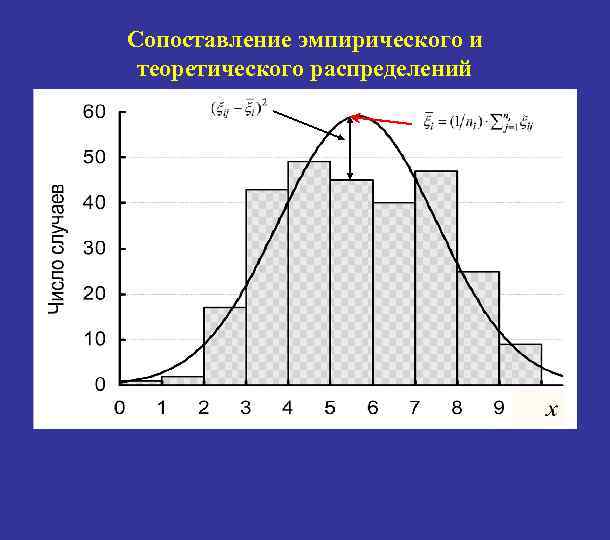 Сопоставление эмпирического и теоретического распределений
Сопоставление эмпирического и теоретического распределений
 Характеристики случайных величин
Характеристики случайных величин
 Моменты случайной величины Начальные моменты Центральные моменты Первый начальный момент математическое ожидание (МО) или среднее значение
Моменты случайной величины Начальные моменты Центральные моменты Первый начальный момент математическое ожидание (МО) или среднее значение
 Второй центральный момент дисперсия D, стандартное (среднеквадратическое) отклонение σ
Второй центральный момент дисперсия D, стандартное (среднеквадратическое) отклонение σ
 Робастные методы оценивания
Робастные методы оценивания
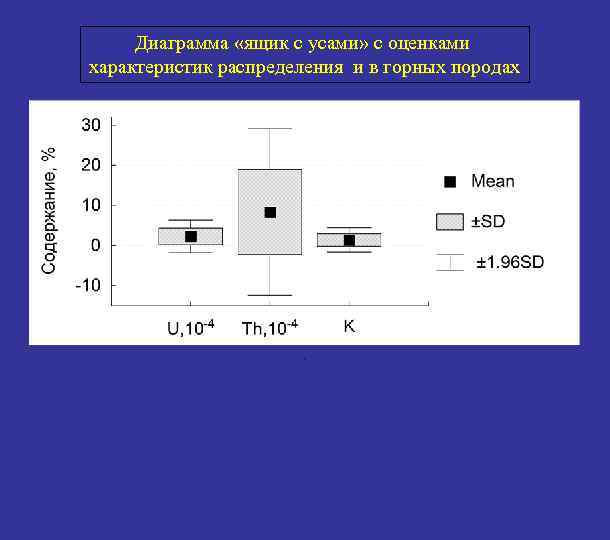 Диаграмма «ящик с усами» с оценками характеристик распределения и в горных породах
Диаграмма «ящик с усами» с оценками характеристик распределения и в горных породах


