МАТЕМАТИЧЕСКАЯ СТАТИСТИКА ИЗ ИСТОРИИ НАУКИ Математическая статистика

МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

ИЗ ИСТОРИИ НАУКИ Математическая статистика возникла в 17 веке. Дальнейшее развитие математической статистики (вторая половина 19 начало 20 -х веков) обязано в первую очередь П. Л. Чебышеву, А. А. Маркову, А. М. Ляпунову, К. Гауссу, А. Кетле, Ф. Гальтону, К Пирсону, и др. В 20 наиболее существенный вклад в математическую статистику был сделан А. Н. Колмогоровым, В. И. Романовским, Е. Е. Слуцким, Н. В. Смирновым, Б. В. Гнеденко, а также английскими учёными Стъюдентом, Р. Фишером, Э. Пирсоном и американскими Ю. Нейманом, А. Вальдом.

Математическая статистика устанавливает закономерности в массовых случайных явлениях

ЗАДАЧИ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ § Сбор и группировка статистического материала, полученного в результате наблюдений над случайными процессами §Анализ полученных статистических данных: üоценка неизвестной вероятности события üоценка неизвестной функции распределения; ü оценка параметров распределения ü оценка зависимости от других случайных величин и т. д. ü проверка статистических гипотез о виде неизвестного распределения или о значениях параметров известного распределения

ОБЪЕКТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ § Качественные признаки изучаемого явления или процесса (стандартность детали) § Количественные признаки (контролируемый размер детали)

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ § Генеральная совокупность – вся совокупность экспериментальных данных § Выборочная совокупность или выборка объема n – определенная часть объектов генеральной совокупности § Выборочный метод: выводы, полученные при изучении выборки, распространяются на всю генеральную совокупность § Репрезентативная (представительная)выборка – это выборка, которая правильно отражает соотношения в генеральной совокупности §Варианты xi - различные значения случайной величины § Вариационный ряд – последовательность вариант xi , записанная в возрастающем порядке

ПРИМЕР 1 Записать в виде вариационного ряда выборку 5, 3, 7, 10, 5, 5, 2, 10, 7, 2, 7, 7, 4, 2, 4. РЕШЕНИЕ Различными в заданной выборке являются элементы х1=2, х2=3, х3=4, х4=5, х5=7, х6=10. Упорядочив элементы выборки по величине, получим вариационный ряд: 2, 2, 2, 3, 4, 4, 5, 5, 5, 7, 7, 10

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ. § Частота mi * - это частота появления в выборке варианты xi Сумма частот mi * равна объему выборки ∑mi * = n § Относительная частота рi * - отношение частоты mi * к объему выборки n: Сумма относительных частот рi * равна единице ∑ р i* = 1 § Cтатистический ряд - соответствие вариант xi и соответствующих им частот mi * (или относительных частот рi * ) Статистический ряд представляет собой первичную форму записи статистического материала

ПРИМЕР 2 Представить статистическое распределение выборки 5, 3, 7, 10, 5, 5, 2, 10, 7, 2, 7, 7, 4, 2, 4. РЕШЕНИЕ Вариационный ряд: 2, 2, 2, 3, 4, 4, 5, 5, 5, 7, 7, 10 Объем выборки n : n = 15 Частоты mi * : варианта x 1 = 2 имеет частоту m 1 *= 3 варианта варианта x 2 = 3 имеет частоту m 2 *= 1 x 3 = 4 имеет частоту m 3 *= 2 x 4 = 5 имеет частоту m 4 *= 3 x 5 = 7 имеет частоту m 5 *= 4 x 6 = 10 имеет частоту m 6 *= 2

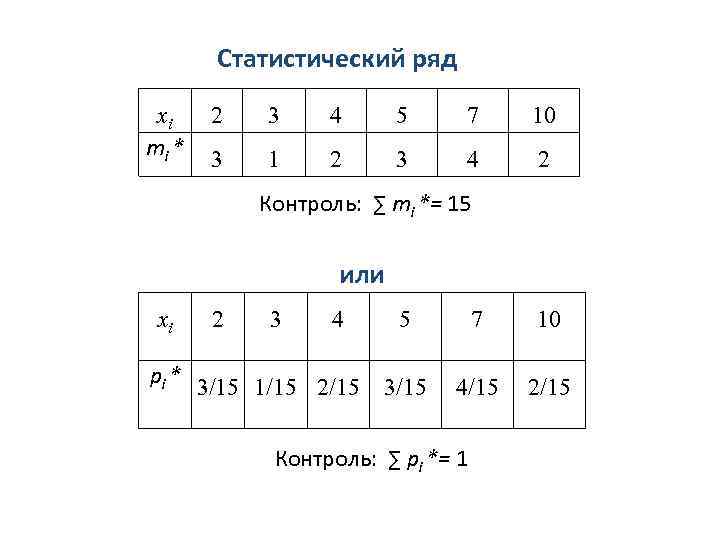Статистический ряд xi mi * 2 3 4 5 7 10 3 1 2 3 4 2 Контроль: ∑ mi *= 15 или xi рi * 2 3 4 3/15 1/15 2/15 5 7 10 3/15 4/15 2/15 Контроль: ∑ pi *= 1

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ. § Интервальный статистический ряд - весь диапазон наблюдаемых значений Х разделяется на интервалы и подсчитывается количество значений xi , приходящееся на каждый интервал Границы интервалов x 1; x 2 ; x 3 . . . xk ; xk+1 . . . Длина интервала h: Количество интервалов рационально выбирать порядка 7 -20

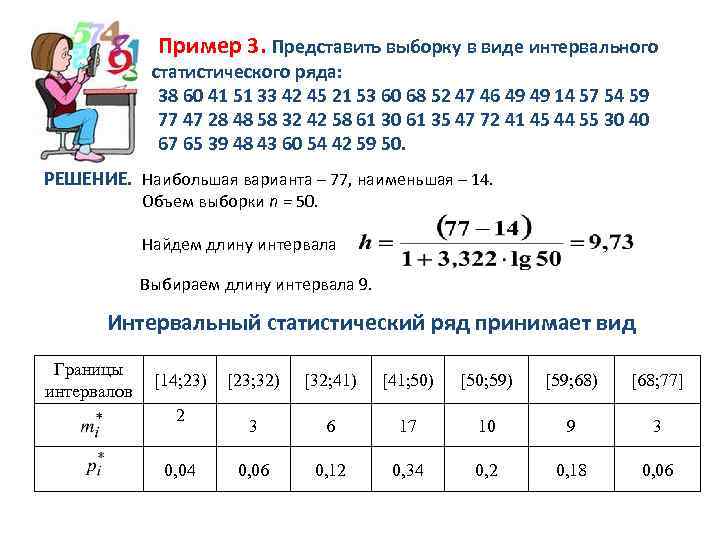Пример 3. Представить выборку в виде интервального статистического ряда: 38 60 41 51 33 42 45 21 53 60 68 52 47 46 49 49 14 57 54 59 77 47 28 48 58 32 42 58 61 30 61 35 47 72 41 45 44 55 30 40 67 65 39 48 43 60 54 42 59 50. РЕШЕНИЕ. Наибольшая варианта – 77, наименьшая – 14. Объем выборки n = 50. Найдем длину интервала Выбираем длину интервала 9. Интервальный статистический ряд принимает вид Границы интервалов [14; 23) 2 0, 04 [23; 32) [32; 41) [41; 50) [50; 59) [59; 68) [68; 77] 3 6 17 10 9 3 0, 06 0, 12 0, 34 0, 2 0, 18 0, 06

ОБРАБОТКА СТАТИСТИЧЕСКИХ ДАННЫХ Построение эмпирической функции распределения Эмпирической функцией распределения F*(X) называют функцию относительной частоты числа наблюдений mx * Пример 4. Построить эмпирическую функцию распределения по результатам наблюдений примера 1. Х 2 3 4 5 7 10 3 1 2 3 4 2

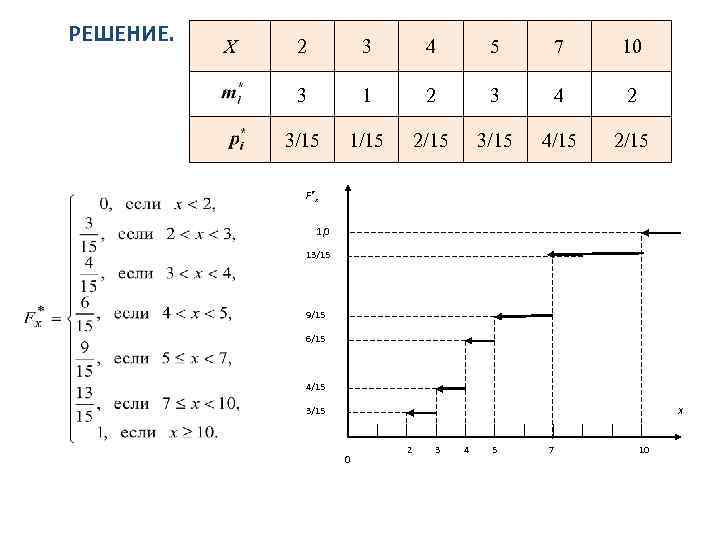РЕШЕНИЕ. Х 2 3 4 5 7 10 3 1 2 3 4 2 3/15 1/15 2/15 3/15 4/15 2/15 F*x 1, 0 13/15 9/15 6/15 4/15 3/15 X 0 2 3 4 5 7 10

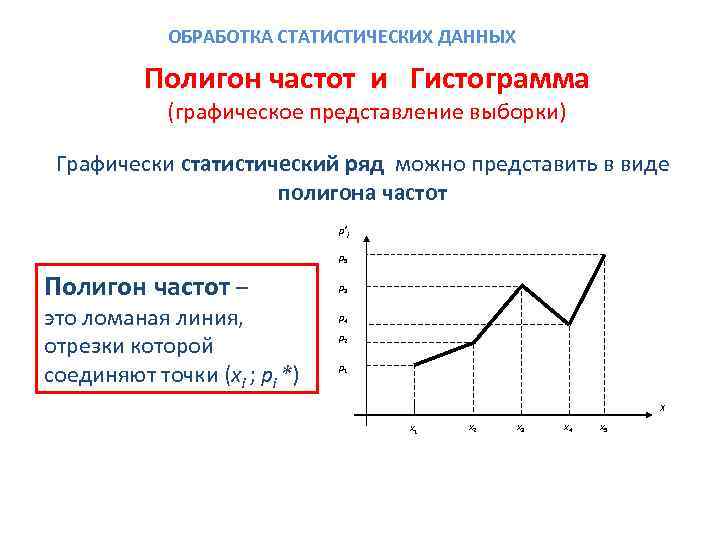ОБРАБОТКА СТАТИСТИЧЕСКИХ ДАННЫХ Полигон частот и Гистограмма (графическое представление выборки) Графически статистический ряд можно представить в виде полигона частот р*i p 5 Полигон частот – это ломаная линия, отрезки которой соединяют точки (хi ; рi *) p 3 p 4 p 2 p 1 X x 1 x 2 x 3 x 4 x 5

Графически интервальный статистический ряд оформляется в виде гистограммы или полигона частот Гистограмма - это ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат отрезки, равные длине интервала, а высотами являются относительные частоты, поделенные на длину интервала. Площадь под гистограммой равна единице. Полигон частот для интервального статистического ряда - это ломаная линия, отрезки которой соединяют точки (хi ; рi *), где хi - середина интервала h X Гистограмма

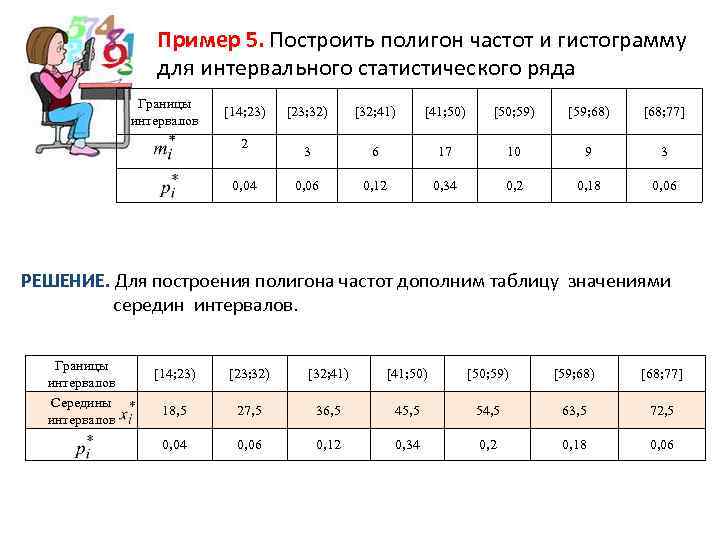Пример 5. Построить полигон частот и гистограмму для интервального статистического ряда Границы интервалов [14; 23) 2 0, 04 [23; 32) [32; 41) [41; 50) [50; 59) [59; 68) [68; 77] 3 6 17 10 9 3 0, 06 0, 12 0, 34 0, 2 0, 18 0, 06 РЕШЕНИЕ. Для построения полигона частот дополним таблицу значениями середин интервалов. Границы интервалов Середины интервалов [14; 23) [23; 32) [32; 41) [41; 50) [50; 59) [59; 68) [68; 77] 18, 5 27, 5 36, 5 45, 5 54, 5 63, 5 72, 5 0, 04 0, 06 0, 12 0, 34 0, 2 0, 18 0, 06

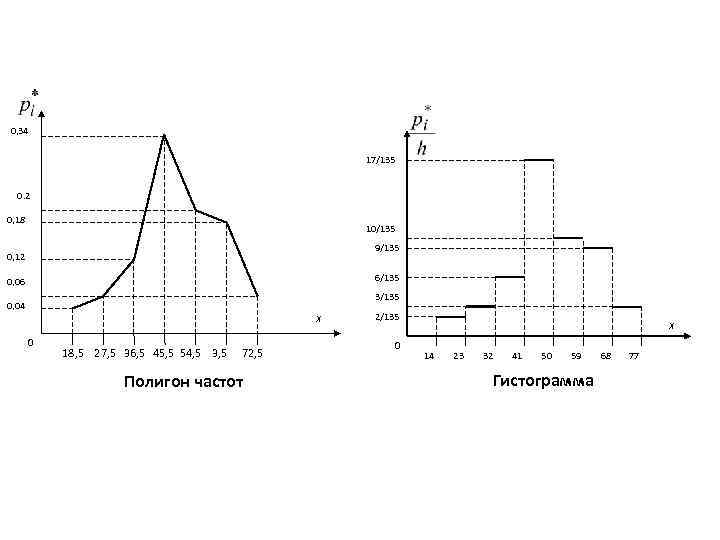0, 34 17/135 0. 2 0, 18 10/135 9/135 0, 12 6/135 0, 06 3/135 0, 04 Х 0 18, 5 27, 5 36, 5 45, 5 54, 5 3, 5 72, 5 Полигон частот 2/135 0 Х 14 23 32 41 50 59 Гистограмма 68 77

ОБРАБОТКА СТАТИСТИЧЕСКИХ ДАННЫХ Точечные оценки параметров распределения Статистическая оценка - приближенное, случайное значение параметра распределения Статистические оценки бывают точечные и интервальные Точечной называют оценку, которая определяется одним числом Точечные оценки q выборочная средняя (оценка математического ожидания) q выборочная дисперсия (оценка дисперсии) q выборочное среднее квадратичное отклонение

Выборочная средняя - это среднее арифметическое значений выборки Для статистического ряда Для интервального ряда -середина интервала k - количество интервалов Выборочная дисперсия Dв – это среднее арифметическое квадратов отклонений наблюдаемых значений от выборочного среднего Для статистического ряда Для интервального ряда

Выборочным средним квадратичным отклонением называют арифметический квадратный корень из выборочной дисперсии Пример 6. Найти оценки параметров распределения (выборочную среднюю, выборочную дисперсию и выборочное среднее квадратичное отклонение) для статистического ряда Решение. xi Объем выборки n = 50. Находим выборочную среднюю: Выборочная дисперсия: Выборочное среднее квадратичное отклонение: 2 7 9 10 8 14 10 18

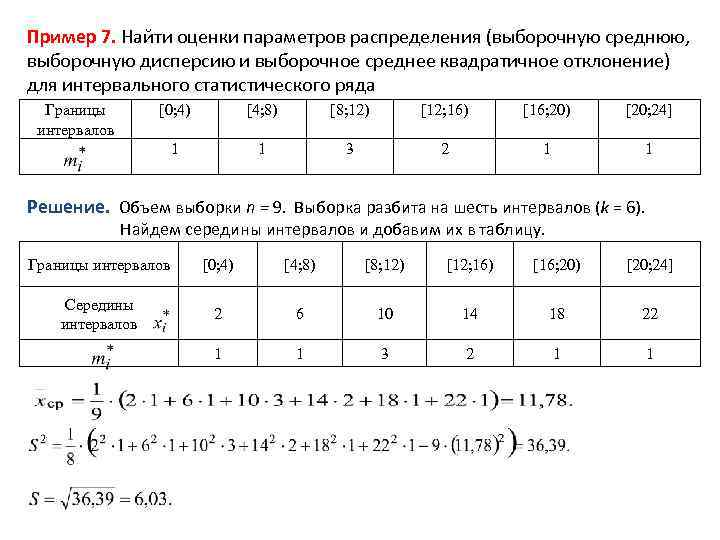Пример 7. Найти оценки параметров распределения (выборочную среднюю, выборочную дисперсию и выборочное среднее квадратичное отклонение) для интервального статистического ряда Границы интервалов [0; 4) [4; 8) [8; 12) [12; 16) [16; 20) [20; 24] 1 1 3 2 1 1 Решение. Объем выборки n = 9. Выборка разбита на шесть интервалов (k = 6). Найдем середины интервалов и добавим их в таблицу. Границы интервалов [0; 4) [4; 8) [8; 12) [12; 16) [16; 20) [20; 24] Середины интервалов 2 6 10 14 18 22 1 1 3 2 1 1

Интервальные оценки параметров распределения Пусть в результате эксперимента получены значения точечных оценок которые группируются вокруг некоторого значения - при истинное значение параметра - оценка параметра | а − ã |→ min | а − ã |<ε Р(| а − ã |< ε )= β – доверительная вероятность Для большинства технических задач β Є [0, 9; 0, 99]

Большие по абсолютной величине ошибки будут появляться с малой вероятностью α =1− β, которую называют вероятностью риска или уровнем значимости Неравенство | а − ã |< ε можно записать в виде −ε<а−ã<ε или ã−ε<а<ã+ε – доверительный интервал q доверительный интервал покрывает неизвестный параметр а с заданной надежностью β q доверительный интервал - это интервал значений параметра а, совместимых с опытными данными и не противоречащих им

Доверительный интервал для математического ожидания: Где −коэффициент Стьюдента(находят по таблице) к = n - 1 - число степеней свободы β - доверительная вероятность Доверительный интервал для дисперсии:

Пример 1. Произведено 20 опытов над случайной величиной X, распределенной по нормальному закону. Требуется построить доверительные интервалы для математического ожидания и дисперсии, соответствующие доверительной вероятности β=0, 8, если получены оценки математического ожидания и : дисперсии: S 2= 0, 064. Решение. По таблице находим значение коэффициента Стьюдента для числа степеней свободы k= n-1=20 -1=19 и доверительной вероятности β=0, 8: Тогда Доверительный интервал для математического ожидания: 10, 78− 0, 751 < M(Х) < 10, 78 + 0, 751, 10, 029 < M(Х) < 11, 531. Для доверительной вероятности β=0, 8 и уровня значимости α=0, 2 по таблице найдем значения распределения : Доверительный интервал для дисперсии: 0, 0447 < D(X) < 0, 1039.

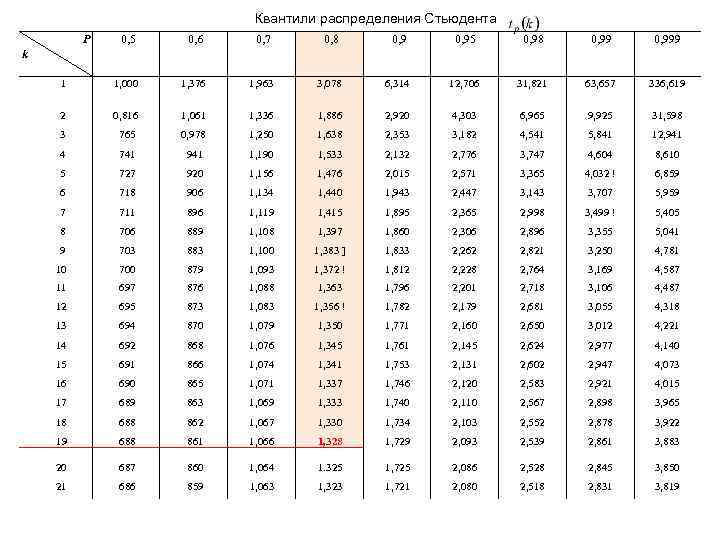Квантили распределения Стьюдента P 0, 5 0, 6 0, 7 0, 8 0, 95 0, 98 0, 999 1 1, 000 1, 376 1, 963 3, 078 6, 314 12, 706 31, 821 63, 657 336, 619 2 0, 816 1, 061 1, 336 1, 886 2, 920 4, 303 6, 965 9, 925 31, 598 3 765 0, 978 1, 250 1, 638 2, 353 3, 182 4, 541 5, 841 12, 941 4 741 941 1, 190 1, 533 2, 132 2, 776 3, 747 4, 604 8, 610 5 727 920 1, 156 1, 476 2, 015 2, 571 3, 365 4, 032 ! 6, 859 6 718 906 1, 134 1, 440 1, 943 2, 447 3, 143 3, 707 5, 959 7 711 896 1, 119 1, 415 1, 895 2, 365 2, 998 3, 499 ! 5, 405 8 706 889 1, 108 1, 397 1, 860 2, 306 2, 896 3, 355 5, 041 9 703 883 1, 100 1, 383 ] 1, 833 2, 262 2, 821 3, 250 4, 781 10 700 879 1, 093 1, 372 ! 1, 812 2, 228 2, 764 3, 169 4, 587 11 697 876 1, 088 1, 363 1, 796 2, 201 2, 718 3, 106 4, 487 12 695 873 1, 083 1, 356 ! 1, 782 2, 179 2, 681 3, 055 4, 318 13 694 870 1, 079 1, 350 1, 771 2, 160 2, 650 3, 012 4, 221 14 692 868 1, 076 1, 345 1, 761 2, 145 2, 624 2, 977 4, 140 15 691 866 1, 074 1, 341 1, 753 2, 131 2, 602 2, 947 4, 073 16 690 865 1, 071 1, 337 1, 746 2, 120 2, 583 2, 921 4, 015 17 689 863 1, 069 1, 333 1, 740 2, 110 2, 567 2, 898 3, 965 18 688 862 1, 067 1, 330 1, 734 2, 103 2, 552 2, 878 3, 922 19 688 861 1, 066 1, 328 1, 729 2, 093 2, 539 2, 861 3, 883 20 687 860 1, 064 1. 325 1, 725 2, 086 2, 528 2, 845 3, 850 21 686 859 1, 063 1, 323 1, 721 2, 080 2, 518 2, 831 3, 819 k

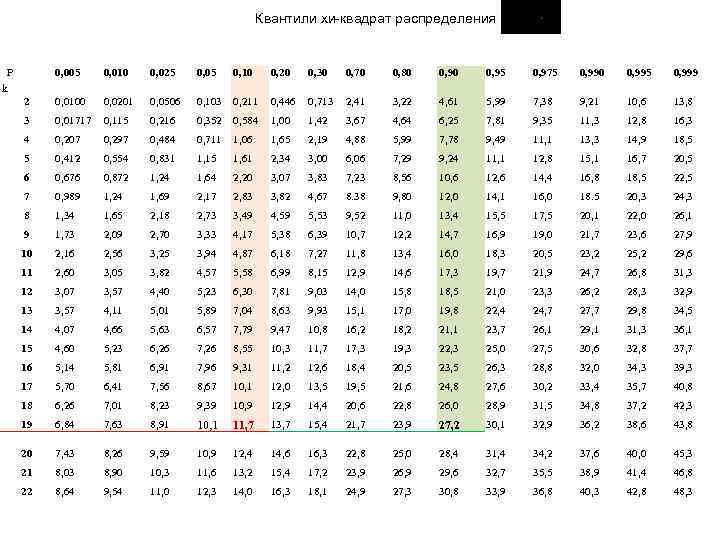Квантили хи-квадрат распределения P 0, 005 0, 010 0, 025 0, 05 0, 10 0, 20 0, 30 0, 70 0, 80 0, 95 0, 975 0, 990 0, 995 0, 999 2 0, 0100 0, 0201 0, 0506 0, 103 0, 211 0, 446 0, 713 2, 41 3, 22 4, 61 5, 99 7, 38 9, 21 10, 6 13, 8 3 0, 01717 0, 115 0, 216 0, 352 0, 584 1, 00 1, 42 3, 67 4, 64 6, 25 7, 81 9, 35 11, 3 12, 8 16, 3 4 0, 207 0, 297 0, 484 0, 711 1, 06 1, 65 2, 19 4, 88 5, 99 7, 78 9, 49 11, 1 13, 3 14, 9 18, 5 5 0, 412 0, 554 0, 831 1, 15 1, 61 2, 34 3, 00 6, 06 7, 29 9, 24 11, 1 12, 8 15, 1 16, 7 20, 5 6 0, 676 0, 872 1, 24 1, 64 2, 20 3, 07 3, 83 7, 23 8, 56 10, 6 12, 6 14, 4 16, 8 18, 5 22, 5 7 0, 989 1, 24 1, 69 2, 17 2, 83 3, 82 4, 67 8. 38 9, 80 12, 0 14, 1 16, 0 18. 5 20, 3 24, 3 8 1, 34 1, 65 2, 18 2, 73 3, 49 4, 59 5, 53 9, 52 11, 0 13, 4 15, 5 17, 5 20, 1 22, 0 26, 1 9 1, 73 2, 09 2, 70 3, 33 4, 17 5, 38 6, 39 10, 7 12, 2 14, 7 16, 9 19, 0 21, 7 23, 6 27, 9 10 2, 16 2, 56 3, 25 3, 94 4, 87 6, 18 7, 27 11, 8 13, 4 16, 0 18, 3 20, 5 23, 2 25, 2 29, 6 11 2, 60 3, 05 3, 82 4, 57 5, 58 6, 99 8, 15 12, 9 14, 6 17, 3 19, 7 21, 9 24, 7 26, 8 31, 3 12 3, 07 3, 57 4, 40 5, 23 6, 30 7, 81 9, 03 14, 0 15, 8 18, 5 21, 0 23, 3 26, 2 28, 3 32, 9 13 3, 57 4, 11 5, 01 5, 89 7, 04 8, 63 9, 93 15, 1 17, 0 19, 8 22, 4 24, 7 27, 7 29, 8 34, 5 14 4, 07 4, 66 5, 63 6, 57 7, 79 9, 47 10, 8 16, 2 18, 2 21, 1 23, 7 26, 1 29, 1 31, 3 36, 1 15 4, 60 5, 23 6, 26 7, 26 8, 55 10, 3 11, 7 17, 3 19, 3 22, 3 25, 0 27, 5 30, 6 32, 8 37, 7 16 5, 14 5, 81 6, 91 7, 96 9, 31 11, 2 12, 6 18, 4 20, 5 23, 5 26, 3 28, 8 32, 0 34, 3 39, 3 17 5, 70 6, 41 7, 56 8, 67 10, 1 12, 0 13, 5 19, 5 21, 6 24, 8 27, 6 30, 2 33, 4 35, 7 40, 8 18 6, 26 7, 01 8, 23 9, 39 10, 9 12, 9 14, 4 20, 6 22, 8 26, 0 28, 9 31, 5 34, 8 37, 2 42, 3 19 6, 84 7, 63 8, 91 10, 1 11, 7 13, 7 15, 4 21, 7 23, 9 27, 2 30, 1 32, 9 36, 2 38, 6 43, 8 20 7, 43 8, 26 9, 59 10, 9 12, 4 14, 6 16, 3 22, 8 25, 0 28, 4 31, 4 34, 2 37, 6 40, 0 45, 3 21 8, 03 8, 90 10, 3 11, 6 13, 2 15, 4 17, 2 23, 9 26, 9 29, 6 32, 7 35, 5 38, 9 41, 4 46, 8 22 8, 64 9, 54 11, 0 12, 3 14, 0 16, 3 18, 1 24, 9 27, 3 30, 8 33, 9 36, 8 40, 3 42, 8 48, 3 k

Корреляционный анализ Выборочный корреляционный момент: Выборочный коэффициент корреляции:

У Х Пример. Найти выборочный коэффициент корреляции по данным корреляционной 5 таблицы : 10 10 20 30 3 - 2 5 4 2 Решение. Составим таблицы отдельно для распределения Х и распределения У: Х 10 20 30 У 5 10 mi * 8 4 4 mj * 5 11 Найдем оценки параметров распределения: Выборочный корреляционный момент: Выборочный коэффициент корреляции: Вывод: зависимость между случайными величинами не линейная

РЕГРЕССИОННЫЙ АНАЛИЗ РЕГРЕССИЯ (лат. regressio — обратное движение) в статистике — статистическая зависимость среднего значения случайной величины от значений другой случайной величины или нескольких случайных величин РЕГРЕССИЯ - количественные изменения одного явления, наступающие в связи с изменениями другого явления, находящегося с первым в корреляционной связи Классические примеры регрессии (Фрэнсис Гальтон, 1886) qзависимость среднего роста детей от роста родителей qзависимость средних диаметров сосен от их высот qзависимость среднего роста человека от его веса и т. п. РЕГРЕССИОННЫЙ АНАЛИЗ - раздел математической статистики, объединяющий практические методы исследования регрессионной зависимости между величинами по статистическим данным ЦЕЛЬ регрессионного анализа – определение аналитического выражения связи ПРИМЕРЫ ЗАДАЧ q. Как ВВП страны зависит от средней заработной платы, мировых цен на нефть и курса рубля? q. Как определить зависимость между погодой и количеством посетителей? q. Как спрогнозировать приток клиентов в зависимости от размера рекламного бюджета? q. Сколько времени нужно производить обжиг, чтобы достигнуть наилучшего качества?

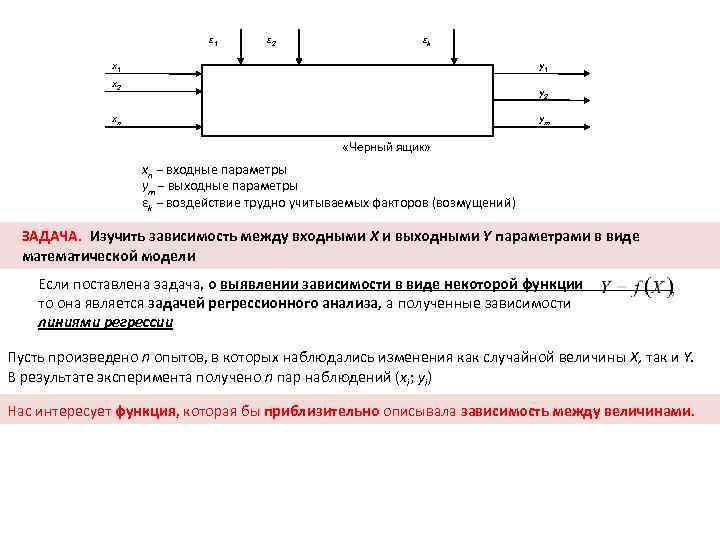ε 1 ε 2 εk x 1 y 1 x 2 y 2 xn ym «Черный ящик» xn − входные параметры ym − выходные параметры εk − воздействие трудно учитываемых факторов (возмущений) ЗАДАЧА. Изучить зависимость между входными X и выходными Y параметрами в виде математической модели Если поставлена задача, о выявлении зависимости в виде некоторой функции то она является задачей регрессионного анализа, а полученные зависимости линиями регрессии Пусть произведено n опытов, в которых наблюдались изменения как случайной величины X, так и Y. В результате эксперимента получено n пар наблюдений (xi; yi) Нас интересует функция, которая бы приблизительно описывала зависимость между величинами.

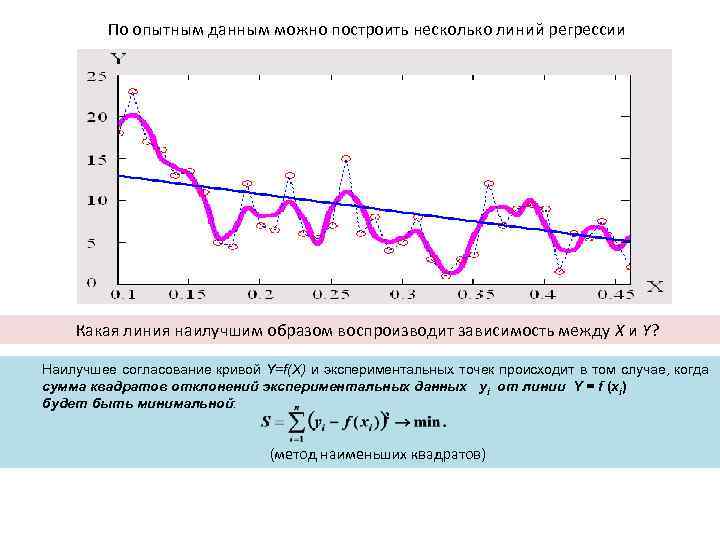По опытным данным можно построить несколько линий регрессии Какая линия наилучшим образом воспроизводит зависимость между X и Y? Наилучшее согласование кривой Y=f(X) и экспериментальных точек происходит в том случае, когда сумма квадратов отклонений эксnериментальных данных yi от линии Y = f (xi) будет быть минимальной: (метод наименьших квадратов)

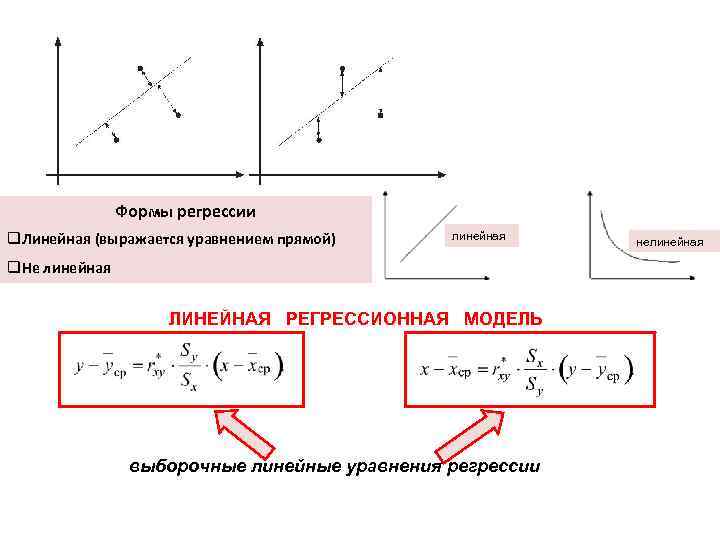Формы регрессии q. Линейная (выражается уравнением прямой) линейная q. Не линейная ЛИНЕЙНАЯ РЕГРЕССИОННАЯ МОДЕЛЬ выборочные линейные уравнения регрессии нелинейная

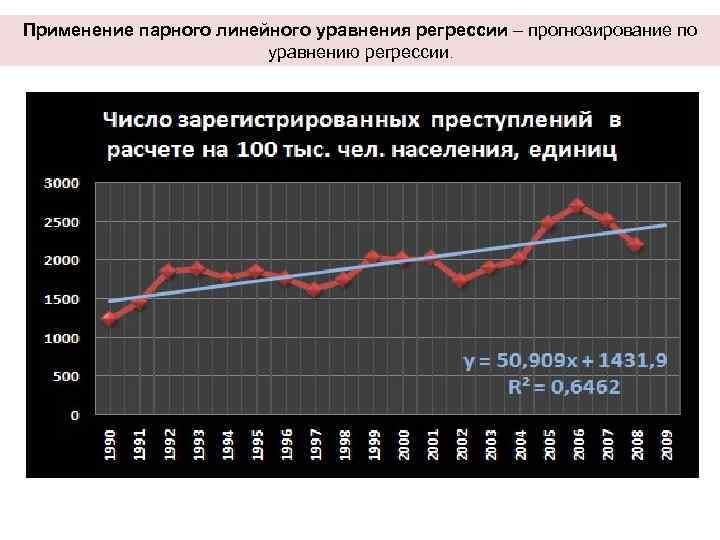Применение парного линейного уравнения регрессии – прогнозирование по уравнению регрессии.

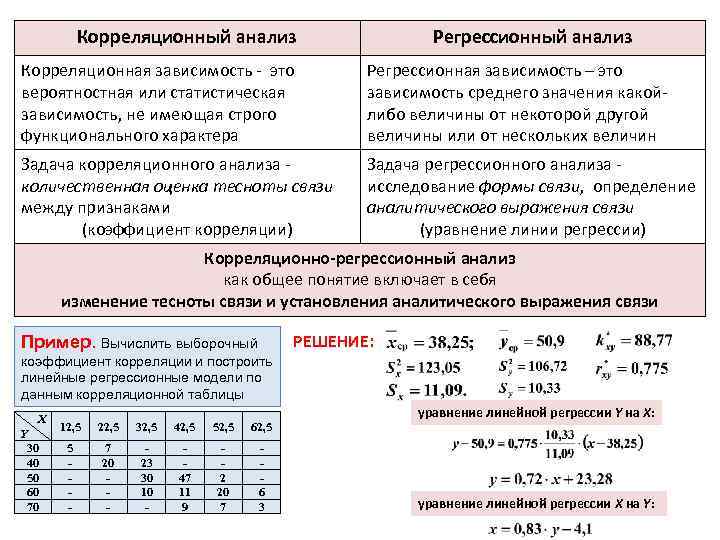Корреляционный анализ Регрессионный анализ Корреляционная зависимость - это вероятностная или статистическая зависимость, не имеющая строго функционального характера Регрессионная зависимость – это зависимость среднего значения какойлибо величины от некоторой другой величины или от нескольких величин Задача корреляционного анализа количественная оценка тесноты связи между признаками (коэффициент корреляции) Задача регрессионного анализа исследование формы связи, определение аналитического выражения связи (уравнение линии регрессии) Корреляционно-регрессионный анализ как общее понятие включает в себя изменение тесноты связи и установления аналитического выражения связи РЕШЕНИЕ: Пример. Вычислить выборочный коэффициент корреляции и построить линейные регрессионные модели по данным корреляционной таблицы X Y 30 40 50 60 70 12, 5 22, 5 32, 5 42, 5 52, 5 62, 5 5 - 7 20 - 23 30 10 - 47 11 9 2 20 7 6 3 уравнение линейной регрессии Y на X: уравнение линейной регрессии X на Y:

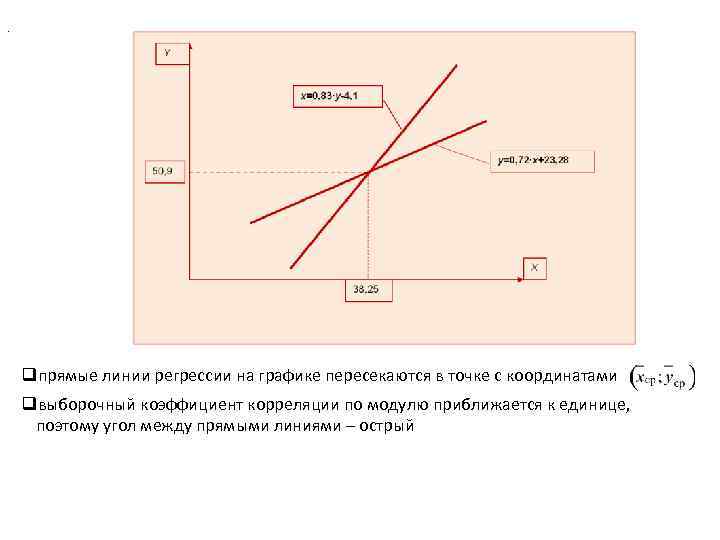. qпрямые линии регрессии на графике пересекаются в точке с координатами qвыборочный коэффициент корреляции по модулю приближается к единице, поэтому угол между прямыми линиями – острый