МАТЕМАТИЧЕСКАЯ ЭКОНОМИКА 32 часа лектор Марченко Ирина

МАТЕМАТИЧЕСКАЯ ЭКОНОМИКА (32 часа) лектор: Марченко Ирина Владимировна 1

Тема 1. Элементы теории процентных ставок 2

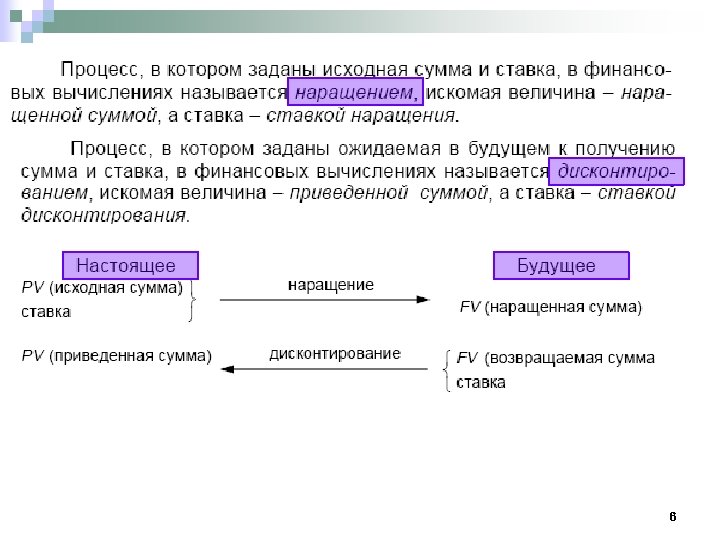
§ 1. 1. Логика финансовых операций. Учет фактора времени Финансовая операция предполагает совокупность условий, согласованных участниками: • сумма кредита (займа, инвестиций), • сроки операции, • способы начисления процентов. Для оценивания результатов фин. операции необходим количественный анализ: совокупность методов расчета. (Финансовая математика, Финансовые и коммерческие расчеты). Принцип: неравноценность сумм, отнесенных к разным моментам времени. Следствие: неправомерность суммирования сумм, отнесенным к разным моментам времени. 3

Простейшим видом финансовой операции является однократное предоставление в долг некоторой суммы PV (present value) с условием, что через некоторое время t будет возвращена большая сумма FV (future value). Результативность подобной сделки может быть оценена различными показателями: 4

. Найдем проценты, процентную ставку, учетную ставку, дисконт-фактор. 5

6

§ 1. 2. Наращение и дисконтирование по простым процентам Схема простых процентов предполагает неизменность суммы с которой начисляются проценты. Пусть PV – инвестируемый капитал r – годовая доходность (процентная ставка) PV • r – величина ежегодного увеличения капитала Через n лет величина инвестируемого капитала составит: – формула наращения по простым процентам. – множитель наращения – проценты (прирост капитала) 7

Наращение по простым процентам в случае, когда продолжительность финансовой операции n не равна целому числу лет, определяется по формуле: (день выдачи и день погашения ссуды принято считать за один день) T – количество дней в году • точные проценты ( точное число дней в году (365 или 366), в квартале (от 89 до 92), в месяце (от 28 до 31); • обыкновенные проценты ( приближенное число дней в году, квартале и месяце (соответственно 360, 90, 30). t – продолжительность финансовой операции в днях • точное число дней ссуды (расчет ведется по дням); • приближенное число дней ссуды (месяц 30 дней). 8

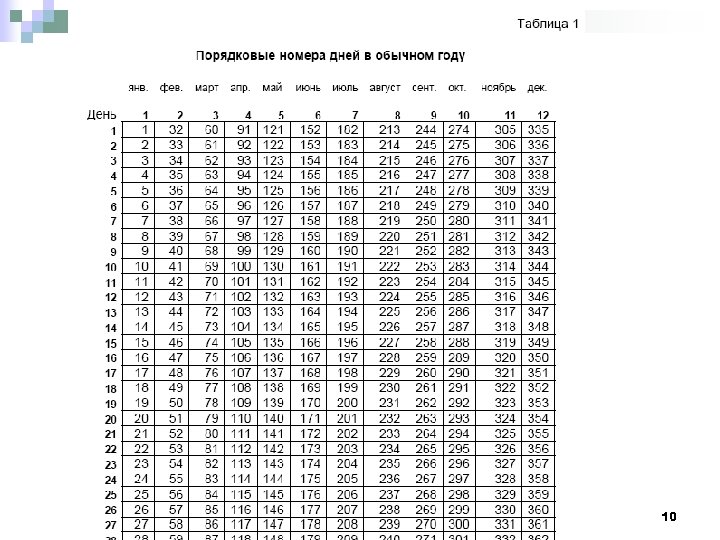
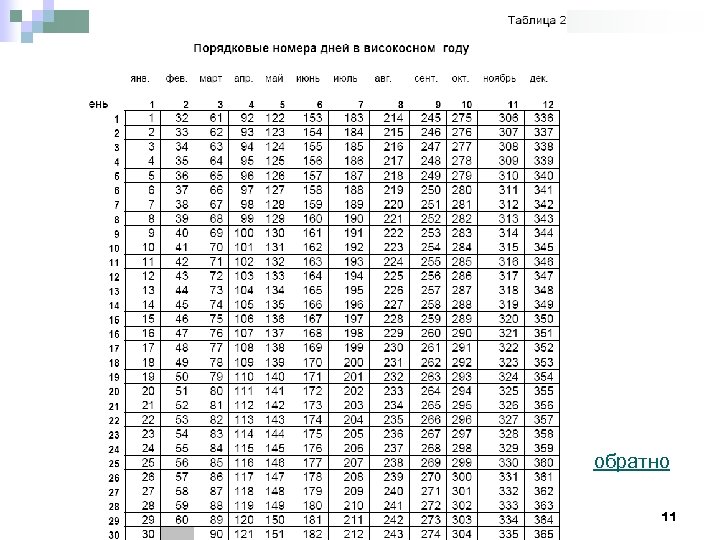
В применяются различные способы расчетов: 1) обыкновенные проценты с приближенным числом дней 2) обыкновенные проценты с точным числом дней 3) точные проценты с точным числом дней Для упрощения процедуры расчета точного числа дней пользуются специальными таблицами (Таблица 1, Таблица 2). 9

10

обратно 11

12

– множитель дисконтирования показывает долю капитала PV в FV – дисконт 13

Владелец векселя на сумму FV предлагает банку купить его раньше срока оплаты векселя по меньшей цене PV – банковское дисконтирование, – дисконтированная величина векселя, – ставка дисконтирования (учетная ставка) – дисконт, удерживаемая в пользу банка сумма Владелец векселя получит: 14

– формула банковского дисконтирования – дисконтный множитель (коэф. дисконтирования) Задача, обратная банковскому дисконтированию, называется наращением по учетной ставке. 15

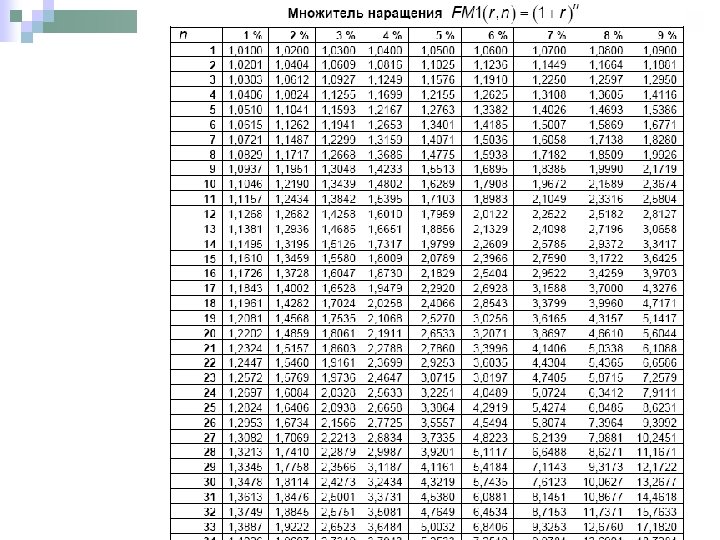
§ 1. 3. Сложные проценты. Номинальная и эквивалентная процентные ставки Инвестиция, сделанная на условиях сложного процента, предполагает, что очередной доход за период начисляется не с первоначальной величины капитала, а с общей суммы, включающей также и ранее начисленные и не востребованные инвестором проценты. – формула наращения по сложным процентам – коэф. наращения по сложным процентам (см. таблицу 3). Экономический смысл: коэф. наращения показывает во сколько раз увеличится капитал в одну единицу через n периодов при заданной процентной ставке r. 16

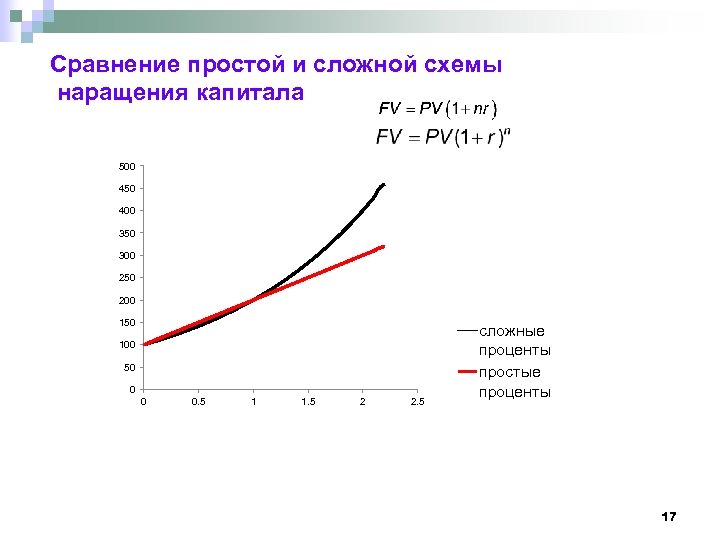Сравнение простой и сложной схемы наращения капитала 500 450 400 350 300 250 200 150 100 50 0 0 0. 5 1 1. 5 2 2. 5 сложные проценты простые проценты 17

18

Финансовые контракты могут заключаться на период, отличающийся от целого числа лет. В этом случае существуют различные методы подсчета наращенной суммы: • по схеме сложных процентов: • по смешанной схеме : – целое число лет – дробная часть года. 19

Начисление сложных процентов несколько раз в году: - годовая процентная ставка при m-разовом количестве начислений в году (номинальная ставка) – длительность периода наращения – процентная ставка за период Формула наращения при m-разовом количестве начислений процентов в году: 20

Эффективная процентная ставка – это годовая ставка сложных процентов, которая дает тот же результат, что и m-разовое начисление процентов по ставке. 21

Если две номинальные годовые процентные ставки и определяют одну и ту же эффективную ставку, они называются эквивалентными: Вычисление номинальной ставки по известной эффективной: 22

Формула, описывающая процесс дисконтирования по сложным процентам имеет вид: – множитель дисконтирования (табл. 4) Экономический смысл множителя дисконтирования: он показывает «сегодняшнюю» цену одной денежной единицы будущего спустя n периодов при ставке доходности r. 23

Формула дисконтирования при m-разовом количестве начислений в году: 24

§ 1. 4. Сложная учетная ставка 25

26

27

§ 1. 5. Учет инфляции 28

29

30

Наращение по схеме простых процентов: Наращение по схеме сложных процентов: 31

32