Matemática Discreta 1 Curso 2007 Prof Eduardo A

Matemática Discreta 1 Curso 2007 Prof. Eduardo A. Canale canale@fing. edu. uy

Información útil n n Web: http: //imerl. fing. edu. uy/matdisc 1/ Web antigua: www. fing. edu. uy/~webimerl/discreta 1/principal. htm n Bibliografía: Matemáticas Discreta y Combinatoria de R. P. Grimaldi. n Elementos de Matemáticas discretas de canale@fing. edu. uy C. L. Liu.

Teórico n n Lunes 13: 30 a 15: 00 Salón A 01 Jueves de 13: 00 a 14: 30 Salón A 11 Coordinador del curso : Nancy Guelman nguelman@fing. edu. uy. canale@fing. edu. uy

Prácticos n n n Iguales a los de la año pasado (WEB) Prácticos: G 4 Mi y Vi 17: 00 a 18: 30 Salón 103 con Sebastián Sensale G 5 Mi y Vi 17: 00 a 18: 30 Salón 014 y 401 con Andrés Corez G 6 Mi y Vi 15: 30 a 17: 00 103 y 101 con Sebastián Sensale

Temas del curso n n n Combinatoria Relaciones Grafos canale@fing. edu. uy

Aprobación del curso n n n Combinatoria, (1 er Parcial) 40 ptos Relaciones 2 do parcial 60 ptos Grafos Exoneración: 60 puntos canale@fing. edu. uy

Combinatoria n n n Técnicas básicas de conteo Inducción completa Principio de Inclusión-exclusión Principio del palomar Relaciones de recurrencia Funciones generatrices canale@fing. edu. uy

Combinatoria n Técnicas básicas de conteo (Grimaldi Cap 1) Reglas de la suma y el producto (1. 1) n Arreglos con y sin repetición (1. 2) n Permutaciones con y sin repetición (1. 2) n Combinaciones sin repetición (1. 3) n Teorema del binomio (1. 3) n Combinaciones con repetición (1. 4) n canale@fing. edu. uy

Combinatoria ¿Qué es la combinatoria? ¿Qué problemas trata de resolver? ¿Para qué sirve? ¿Cuándo surgió? canale@fing. edu. uy

Combinatoria ¿Qué es la combinatoria? Del lat. combināre = com binare Com = unir Binare= dos cosas. Unir dos o más cosas para formar un nuevo objeto. canale@fing. edu. uy

Combinatoria Combinación de objetos: n ¿Se puede? n ¿Cómo? n ¿Cuánto? n Propiedades canale@fing. edu. uy

Combinatoria Combinación de objetos: n ¿Se puede? Existencia n ¿Cómo? Algoritmos n ¿Cuánto? Conteo n Propiedades: Estudio cualitativo (Grafos) canale@fing. edu. uy

Técnicas básicas de conteo n Regla del producto: Si para formar los objetos en el 1 er paso tenemos m posibles salidas y en el segundo n posibles salidas independientes del paso anterior el total de objetos formados será m n canale@fing. edu. uy

Técnicas básicas de conteo n Regla del producto Arreglos con repetición ARmn = mn n Arreglos sin repetición Amn = m(m-1)…(m-n+1) n Permutaciones (sin repetición): Amm = m! n Arreglos con repetición n canale@fing. edu. uy

Libros de matemática n http: //bibliotecabochini. netfirms. com/informacion. htm canale@fing. edu. uy

Permutaciones con repetición n Ejemplo: 1. aab, aba, baa Son 3 en lugar de 3! = 6. 2. aabc, aacb, abac, abca, acab, acba, baac, baca, bcaa, caab, caba, cbaa Son 12 en lugar de 4! = 24. canale@fing. edu. uy

Permutaciones con repetición n Regla general: la cantidad de permutaciones de una palabra aaaabbbbcccc… es igual a Donde n 1, n 2, n 3… es la cantida de a’s, b’s, c’s, etc Obviamnete n 1 + n 2 + n 3 + … nk = n. canale@fing. edu. uy

Permutaciones con repetición n Ejemplo: Tableros de ta-te-ti canale@fing. edu. uy

Permutaciones con repetición n Ejemplo: Tableros de ta-te-ti canale@fing. edu. uy

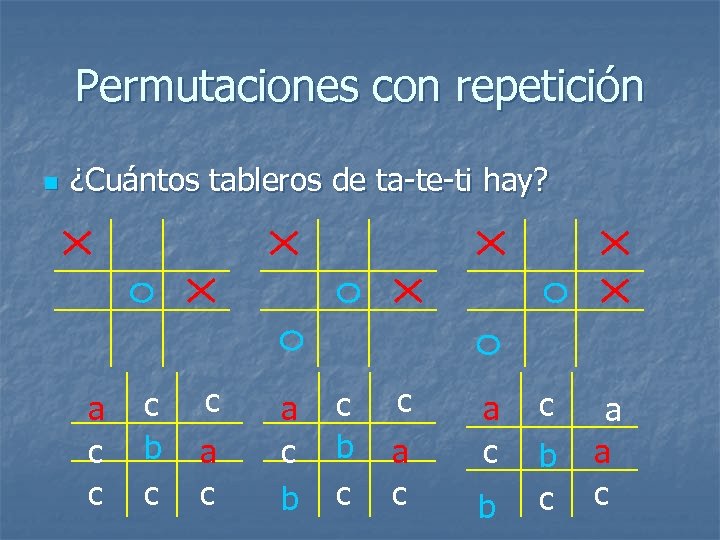Permutaciones con repetición n ¿Cuántos tableros de ta-te-ti hay? a c c c b c c a c a c b c b c a a c

Permutaciones con repetición n ¿Cuántos tableros de ta-te-ti hay? acccbacccbabcc acacbabcc a c c b a c c c b c c canale@fing. edu. uy a

Permutaciones con repetición n ¿Cuántos tableros de ta-te-ti hay? acccbacccbabcc 9!/(2!1!6!)=9 x 8 x 7/2 =252 acacbabcc 9!/(3!2!4!)=9 x 8 x 7 x 6 x 5/12=1260 9!/(2!2!5!)=9 x 8 x 7 x 6/4= 756 canale@fing. edu. uy

Permutaciones con repetición n n El total se obtiene sumando los totales parciales. Hemos aplicado la Regla de la suma que dice así: si los objetos que quiero contar los puedo dividir en dos ( o más) tipos distinto, basta contar cuantos de cada tipo hay y sumar los resultados. canale@fing. edu. uy

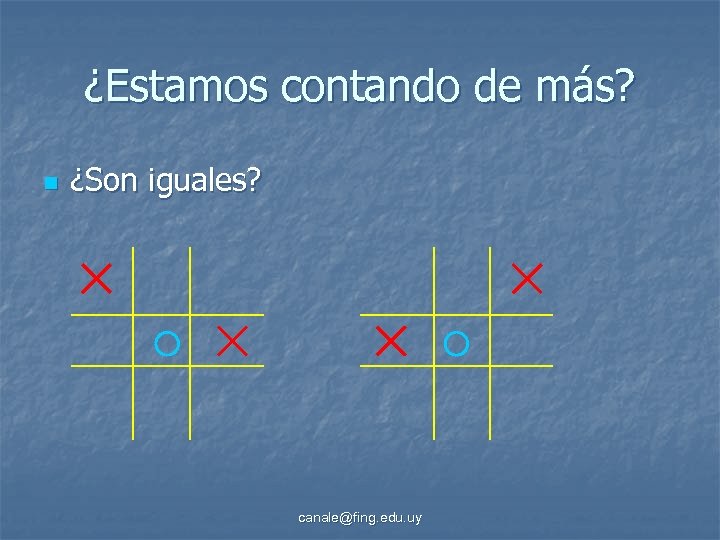¿Estamos contando de más? n ¿Son iguales? canale@fing. edu. uy

Simetrías n n n Suele dar lugar a problemas difíciles Teoría de Redfield y Polya: ver por ejemplo Grimaldi 16. 9 a 16. 11 involucra teoría de grupos (Discreta 2) y funciones generatrices Casos sencillos: permutaciones circulares, combinaciones canale@fing. edu. uy

Permutaciones circulares n n n Ejemplo: tengo cuatro personas a, b, c y d ¿Cuántas formas hay de ubicarlas en una mesa circular? Sea “x” dicha cantidad a d b b c c a c d canale@fing. edu. uy b d a

Permutaciones circulares n n n Paso 1 : elijo una de las x permutaciones circulares Paso 2: la giro de 4 formas posibles Obtengo: todas las 4! Permutaciones (regla del producto) x 4=P=4! a x = 4!/4 = 3! b = d c a = c b canale@fing. edu. uy b d a

Permutaciones circulares n n n En general si tengo n símbolos Hay n giros posibles x n = n! De donde x = n!/n = (n-1)! ¡Qué formula más sencilla! ¿Habrá otra forma de pensarla directamente que de ese resultado? canale@fing. edu. uy

Permutaciones circulares n n Otra forma de pensarlo Fijo a arriba y permuto las otras (n-1) a a d b c c a b d canale@fing. edu. uy … b d c

Simetrías n La combinatoria involucra: Objetos: generalmente cantidad finita de tipos n Forma de combinarlos: geometría (lineal, circular, cuadrada, etc) n Simetría: asociada (a la geometría) o ad hoc. n canale@fing. edu. uy

Combinaciones (sin repetición) n n n n Otra simetría sencilla: toda permutación da lugar a objetos equivalentes = “no importa el orden” Ejemplo: Arreglos de 4 en 3. Objetos: a, b, c, d acd = adc = dac = etc ¿Cuántos tenemos? 3! = 6: acd = adc = cad = cda = dac = dca canale@fing. edu. uy

Combinaciones n n Permutando las combinaciones obtenemos los arreglos, por lo tanto (regla del producto) Cnm n! = Anm Cnm= Anm/ n! = m! (m-n)! n! canale@fing. edu. uy

Combinaciones con repetición n n Ejemplo: ¿De cuántas formas puedo pedir una media docena de biscochos? Supongamos cuatro tipos: a, b, c, d ¿Importa el orden? Ejemplos: aaabbb, aabbcc, etc canale@fing. edu. uy

Combinaciones con repetición n n n n aaabbb = 3 a y 3 b, 0 c, 0 d aabbcc = 2 a, 2 b y 2 c, 0 d 3 a y 3 b = a xxx, b xxx, c 0, d, 0 2 a, 2 b y 2 c = a xx, b xx, c xx, d 0 aaabbb = xxx|| aabbcc = xx|xx|xx| ¿abbcdd? x|xx|x|xx canale@fing. edu. uy

Combinaciones con repetición n n n aaabbb = xxx|| aabbcc = xx|xx|xx| abbcdd =x|xx|x|xx 1 ero) siempre hay 6 “x” y 3 “|” 2 do ) cualquier permutación de 6 x y 3 | da lugar a una elección distinta ¿Cuántas hay? canale@fing. edu. uy

Combinaciones con repetición n ¿Cuántas hay? Permutaciones con repetición de 6+3 letras con 6 y 3 repetidas = (6+3)!/(6!3!) = C 93 En general para CRmn son n “x” y m-1 “|” Total: (n+m-1)! = Cnn+m-1 n!(m-1)! canale@fing. edu. uy

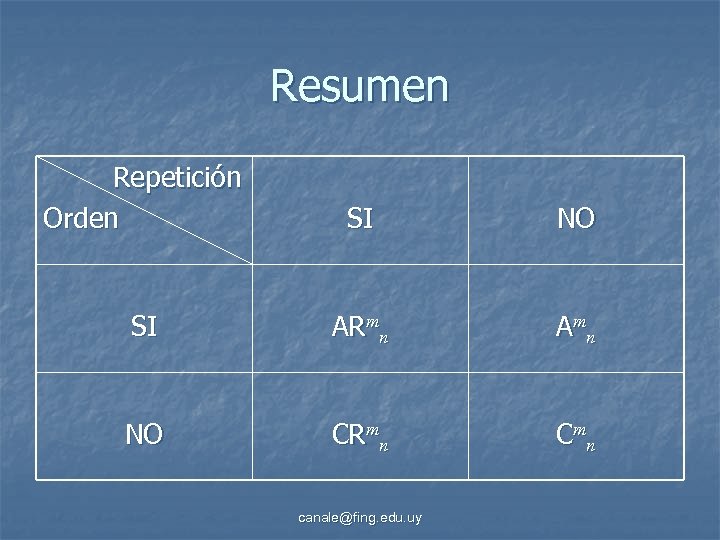Resumen Repetición Orden SI NO SI ARmn A mn NO CRmn C mn canale@fing. edu. uy

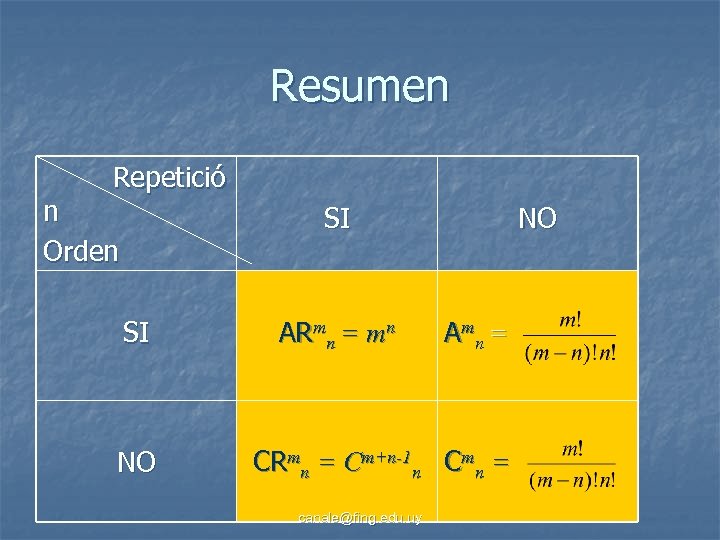Resumen Repetició n Orden SI SI NO ARmn = mn NO A mn = CRmn = Cm+n-1 n Cmn = canale@fing. edu. uy

Otra forma de ver las cosas n n n Combinaciones con repetición de 4 en 6 aaabbb = xxx|| = 3+3+0+0 Distribución de objetos en cajas: objetos y cajas distinguibles o no. Pueden haber cajas vacías o no. canale@fing. edu. uy

Distribución de objetos en cajas Objetos Distiguibles Cajas Distinguibles SI NO SI ? (fácil) CRmn NO ? (no tanto) ? (difícil) canale@fing. edu. uy

Otra forma de ver las cosas n n Fórmula del Binomio: Por esta razón a los coeficientes Cni también se los llama coeficientes binomiales. Se los suele denotar de la siguiente forma canale@fing. edu. uy

Fórmula del Binomio n n n n Demostración combinatoria (a+b)2 = (a+b)= (a 1+b 1) (a 2+b 2) = (a 1+b 1) a 2+ (a 1+b 1) b 2= a 1 a 2 +b 1 a 2+ a 1 b 2 +b 1 b 2 (a+b)3 = (a 1+b 1) (a 2+b 2) (a 3+b 3)= (a 1 a 2 +b 1 a 2+ a 1 b 2 +b 1 b 2) (a 3+b 3)= a 1 a 2 a 3 +b 1 a 2 a 3+ a 1 b 2 a 3 +… + a 1 b 2 b 3 + b 1 b 2 b 3 canale@fing. edu. uy

Fórmula del Binomio n n n Demostración combinatoria a 1 a 2 a 3 +b 1 a 2 a 3+ a 1 b 2 a 3 +… + a 1 b 2 b 3 + b 1 b 2 b 3 Vemos que por cada término comienza con una a 1 o una b 1 sigue con a 2 o b 2 y termina con a 3 o b 3. Entonces podemos pensar que los términos se construyen en un proceso de tres pasos: Paso 1 Elijo una de las letras del 1 er factor (a 1+b 1) Paso 2 Elijo una de las letras del 2 do factor (a 2+b 2) Paso 3 Elijo una de las letras del 3 er factor (a 3+b 3) canale@fing. edu. uy

Fórmula del Binomio n n n Por otro lado los términos finales se obtiene al borrar los índices y juntar los términos iguales. En el ejemplo: aaa +baa+ aba +… + abb + bbb = a 3+3 a 2 b+3 ab 2+b 3 ¿De donde sale el “ 3” de “a 2 b” ? De juntar aab+aba+baa, es decir de elegir en dos pasos “a” y en el otro “b”. ¿De cuantas formas se pueden elegir 2 “a”? Tengo 3 factores, debo elegir 2 de donde elegir dichas “a”, como no importa el orden en que elija dichos dos factores, tengo C 32 formas de hacerlo. canale@fing. edu. uy

Fórmula del Binomio n n En general (a+b)n = i aibn-i Donde i será todas las formas de elegir en i pasos la letra “a”, es decir elegir i factores de entre n: Cni. canale@fing. edu. uy

Algunas Consecuencias n n n Ejemplo 1: (1+x)n = Cni 1 ixn-i= Cni xn-i =(x+1)n = Cni xi 1 n-i= Cni xi Por lo tanto: Cni = Cnn-i Ejemplo 2: 0= (-1+1)n = Cni (-1)i 1 n-i= Cni (-1)i Ejemplo 3: 2 n = (1+1)n = Cni (1)i 1 n-i= Cni Este ejemplo además nos da una cota (grosera) de los coeficientes binomiales. canale@fing. edu. uy