Martin Kay Stanford University Martin Kay String Matching

Martin Kay Stanford University Martin Kay String Matching 1 1

Naive Search (1) naive_search(Pattern, Text, 1) : append(Pattern, _, Text). naive_search(Pattern, [_ | Text], N) : naive_search(Pattern, Text, N 0), N is N 0+1. naive_search("is", "mississippi", N). N=2? ; N=5? ; no | ? Martin Kay String Matching 1 2

pref — A Prefix Predicate Make an entry in the data base every time the predicate is called. pref(P, T) : assert(stat(T, P)), fail. pref([], _). pref([H | P], [H | T]) : pref(P, T). Martin Kay String Matching 1 3

Search using pref naive_search 1(Pattern, Text, 1) : pref(Pattern, Text). naive_search 1(Pattern, [_ | Text], N) : naive_search 1(Pattern, Text, N 0), N is N 0+1. | ? - naive_search 1([i, s], [m, i, s, s, i, p, p, i], N). N=2? ; N=5? ; no | ? Martin Kay String Matching 1 4

The Statistics | ? - listing(stat). stat([m, i, s, s, i, p, p, i], [i, s]). stat([i, s, s, i, p, p, i], [i, s]). stat([s, s, i, p, p, i], [s]). stat([s, i, s, s, i, p, p, i], []). stat([s, s, i, p, p, i], [i, s]). stat([s, i, s, s, i, p, p, i], [i, s]). stat([s, s, i, p, p, i], [s]). stat([s, i, p, p, i], []). stat([s, s, i, p, p, i], [i, s]). stat([i, p, p, i], [i, s]). stat([p, i], [i, s]). stat([], [s]). stat([], [i, s]). 18 Entries 11 Allignments Martin Kay String Matching 1 5

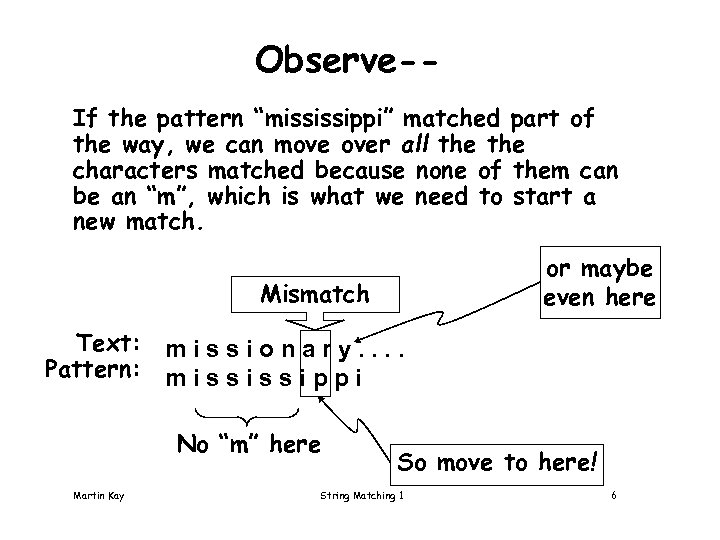Observe-If the pattern “mississippi” matched part of the way, we can move over all the characters matched because none of them can be an “m”, which is what we need to start a new match. or maybe even here Mismatch Text: m i s s i o n a r y. . Pattern: m i s s i p p i No “m” here Martin Kay So move to here! String Matching 1 6

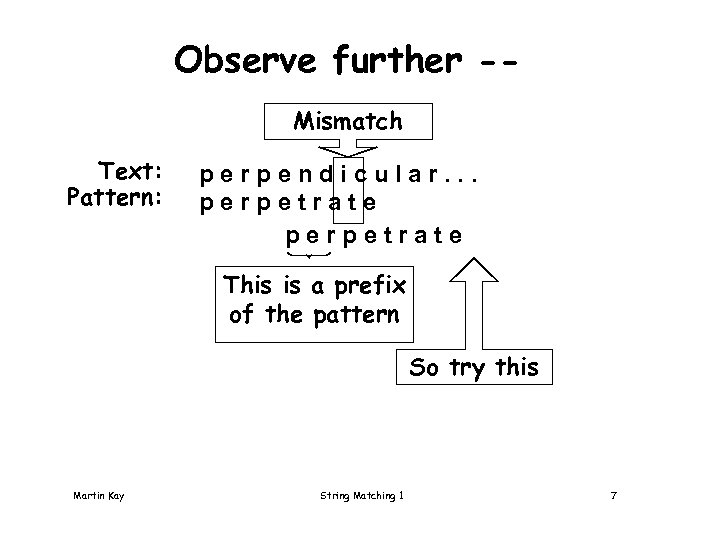Observe further -Mismatch Text: Pattern: perpendicular. . . perpetrate This is a prefix of the pattern So try this Martin Kay String Matching 1 7

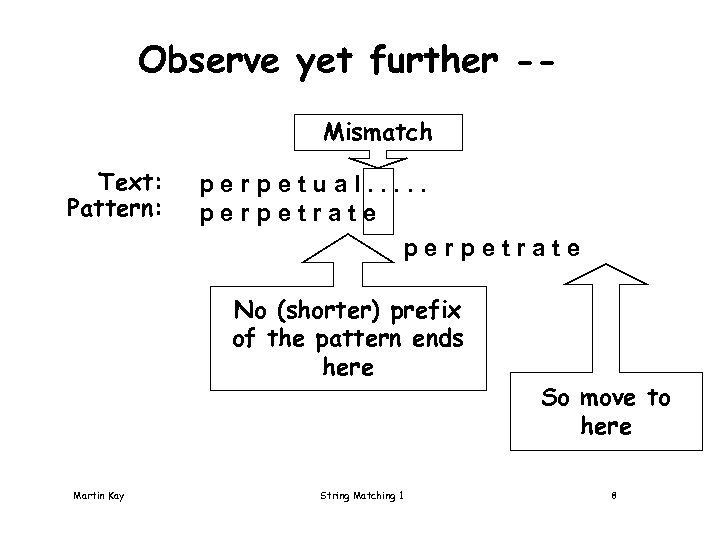Observe yet further -Mismatch Text: Pattern: perpetual. . . perpetrate No (shorter) prefix of the pattern ends here Martin Kay String Matching 1 So move to here 8

Search for abacabadabacaba Overlaps in the text ababacabadabacababa abacabadabacaba abacabadabacaba abacabadabacaba Martin Kay String Matching 1 9

Search for abacabadabacaba Déja vu in the text ababacabadabacababa abacabadabacaba abacabadabacaba abacabadabacaba Martin Kay String Matching 1 10

On-line search We have seen this much of the text so far: caca c We are looking for the pattern cacao. We have some number (0 or more) searches in progress and are waiting for the next character to see which ones continue and maybe to start a new one. caca ca Martin Kay c c String Matching 1 11

Search for abacabadaba in the text 1. The rightmost pointer always moves. c 2. b. Others pointers move if they can a a do so over the same character 3. A new ‘ 0’ is introduced on the left ababacabadabacababa 0 a [0] 1 b [0, 1] 2 a [0, 2] 3 b [0, 1, 3] 4 a [0, 2] 5 c [0, 1, 3] 6 a [0, 4] 7 b [0, 1, 5] 8 a [0, 2, 6] 9 d [0, 1, 3, 7] 10 a [0, 8] 11 b [0, 1, 9] 12 a [0, 2, 10] 13 c [0, 1, 3, 11] 14 a [0, 4, 12] 15 b [0, 1, 5, 13] 16 a [0, 2, 6, 14] result 2 17 d [0, 1, 3, 7] 18 a [0, 8] 19 b [0, 1, 9] 20 a [0, 2, 10] 21 c [0, 1, 3, 11] 22 a [0, 4, 12] 23 b [0, 1, 5, 13] 24 a [0, 2, 6, 14] result 10 25 b [0, 1, 3, 7] 26 a [0, 2] A pointer in a given position always has pointers in the same set of positions to its left These are properties of the pattern only. Therefore they can be cached or precompiled. Martin Kay String Matching 1 12

Search for abacabadabacaba ababacabadabacababa 0 a [0] 1 b [0, 1] 2 a [0, 2] 3 b [0, 1, 3] 4 a [0, 2] 5 c [0, 1, 3] 6 a [0, 4] 7 b [0, 1, 5] 8 a [0, 2, 6] 9 d [0, 1, 3, 7] 10 a [0, 8] 11 b [0, 1, 9] 12 a [0, 2, 10] 13 c [0, 1, 3, 11] 14 a [0, 4, 12] Martin Kay If this matches. . . then so will these String Matching 1 15 b [0, 1, 5, 13] 16 a [0, 2, 6, 14] result 2 17 d [0, 1, 3, 7] 18 a [0, 8] 19 b [0, 1, 9] 20 a [0, 2, 10] 21 c [0, 1, 3, 11] 22 a [0, 4, 12] 23 b [0, 1, 5, 13] 24 a [0, 2, 6, 14] result 10 25 b [0, 1, 3, 7] 26 a [0, 2] 13

Search for abacabadabacaba ababacabadabacababa 0 a [0] 1 b [0, 1] 2 a [0, 2] 3 b [0, 1, 3] 4 a [0, 2] 5 c [0, 1, 3] 6 a [0, 4] 7 b [0, 1, 5] 8 a [0, 2, 6] 9 d [0, 1, 3, 7] 10 a [0, 8] 11 b [0, 1, 9] 12 a [0, 2, 10] 13 c [0, 1, 3, 11] 14 a [0, 4, 12] Martin Kay So try these only if this fails! String Matching 1 15 b [0, 1, 5, 13] 16 a [0, 2, 6, 14] result 2 17 d [0, 1, 3, 7] 18 a [0, 8] 19 b [0, 1, 9] 20 a [0, 2, 10] 21 c [0, 1, 3, 11] 22 a [0, 4, 12] 23 b [0, 1, 5, 13] 24 a [0, 2, 6, 14] result 10 25 b [0, 1, 3, 7] 26 a [0, 2] 14

0 1 2 3 4 5 6 7 8 9 10 11 12. . . a b a c a b a d a b a c a. . . 0 0 1 2 3 4. . . a [0] b [0, 1] a [0, 2] b [0, 1, 3] a [0, 2] c [0, 1, 3] a [0, 4] b [0, 1, 5] a [0, 2, 6] d [0, 1, 3, 7] a [0, 8] b [0, 1, 9] a [0, 2, 10] c [0, 1, 3, 11] a [0, 4, 12] Martin Kay The failure function String Matching 1 15

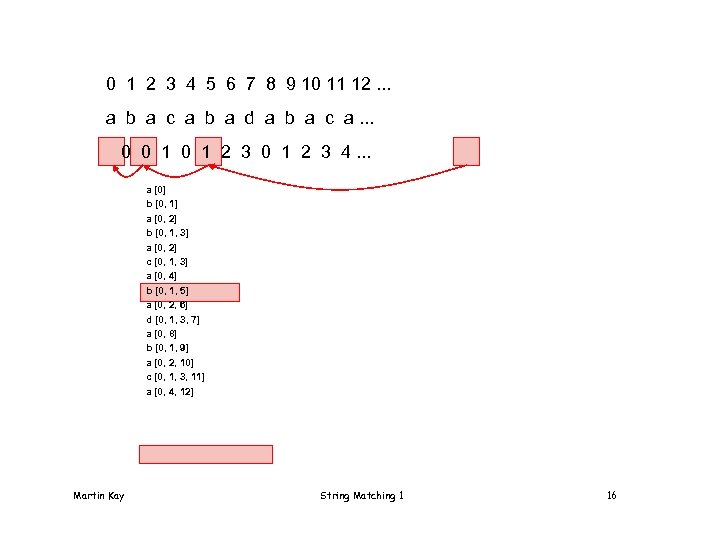0 1 2 3 4 5 6 7 8 9 10 11 12. . . a b a c a b a d a b a c a. . . 0 0 1 2 3 4. . . a [0] b [0, 1] a [0, 2] b [0, 1, 3] a [0, 2] c [0, 1, 3] a [0, 4] b [0, 1, 5] a [0, 2, 6] d [0, 1, 3, 7] a [0, 8] b [0, 1, 9] a [0, 2, 10] c [0, 1, 3, 11] a [0, 4, 12] Martin Kay String Matching 1 16

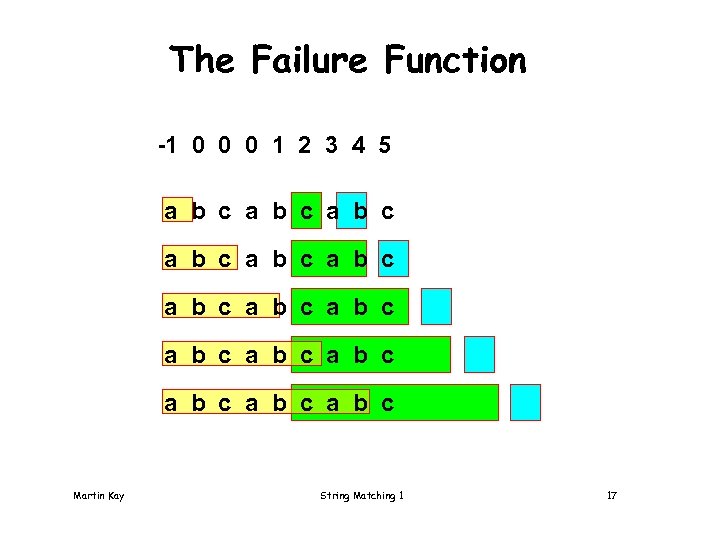The Failure Function -1 0 0 0 1 2 3 4 5 a b c a b c a b c a b c Martin Kay String Matching 1 17

The Failure Function -1 0 0 1 2 3 4 5 6 a b a c a b a d a b a c a b a a b a c a b a d a b a c a b a Martin Kay String Matching 1 18

The Failure Function -1 0 0 1 2 3 4 5 6 a b a c a b a d a b a c a b a a b a c a b a d a b a c a b a Martin Kay String Matching 1 19

Substring, Prefix, Suffix • • • Part of a string S (even if it covers the whole of S) is a substring of S. If it includes the first (last) character of S, it is a prefix (suffix) of S. If it does not cover the whole of S, it is a proper substring (prefix, suffix) of S. Example: S = ababac Some substrings: ababac, ab, b, bab, ac, only ababac is not proper Some prefixes: ababac, a, aba, only ababac is not proper is the Some suffixes: ababac, c, empty string only ababac is not proper Martin Kay String Matching 1 20

Borders • If B is a proper prefix and a proper suffix of a string S, it is a border of S. Examples: abcabcabc has borders abc, abcabc, abacabadabacaba has borders abacaba, a, • Note is a border of every string Martin Kay String Matching 1 21

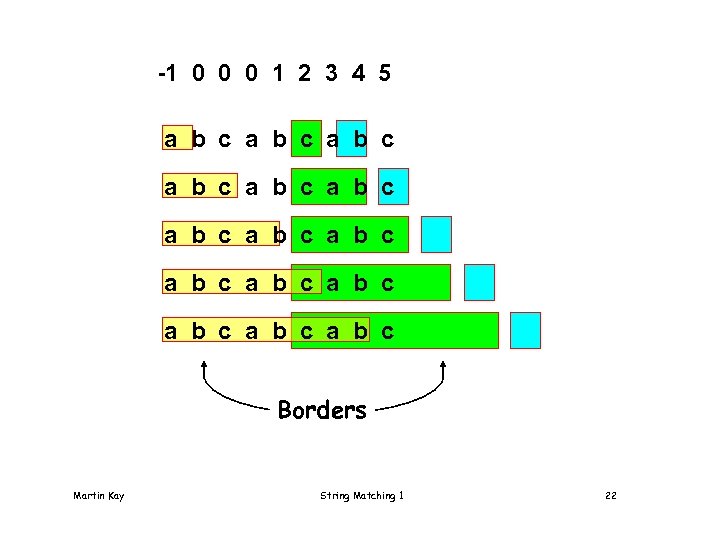-1 0 0 0 1 2 3 4 5 a b c a b c a b c a b c Borders Martin Kay String Matching 1 22

border in Prolog border(Pattern, Border) : append([_ | _], Border, Pattern), append(Border, _, Pattern). Martin Kay String Matching 1 23

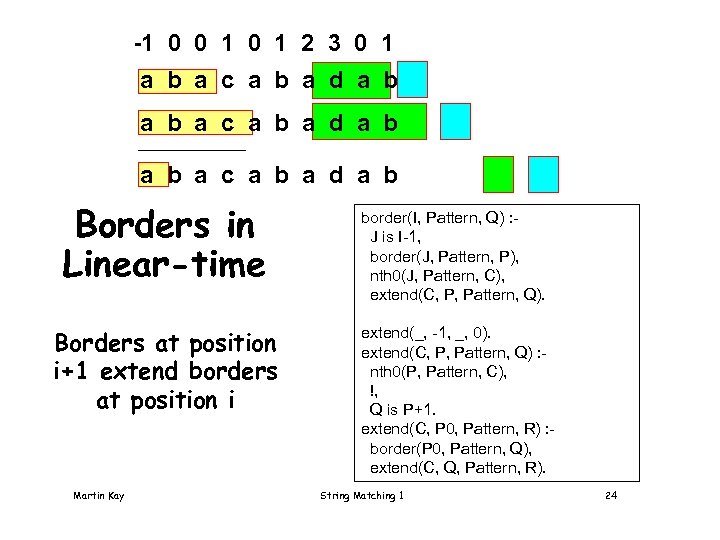-1 0 0 1 2 3 0 1 a b a c a b a d a b Borders in Linear-time Borders at position i+1 extend borders at position i Martin Kay border(I, Pattern, Q) : J is I-1, border(J, Pattern, P), nth 0(J, Pattern, C), extend(C, P, Pattern, Q). extend(_, -1, _, 0). extend(C, P, Pattern, Q) : nth 0(P, Pattern, C), !, Q is P+1. extend(C, P 0, Pattern, R) : border(P 0, Pattern, Q), extend(C, Q, Pattern, R). String Matching 1 24

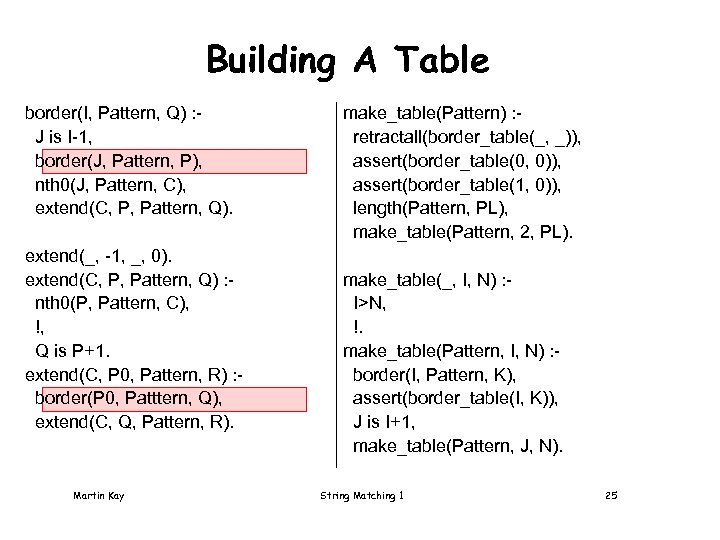Building A Table border(I, Pattern, Q) : J is I-1, border(J, Pattern, P), nth 0(J, Pattern, C), extend(C, P, Pattern, Q). extend(_, -1, _, 0). extend(C, P, Pattern, Q) : nth 0(P, Pattern, C), !, Q is P+1. extend(C, P 0, Pattern, R) : border(P 0, Patttern, Q), extend(C, Q, Pattern, R). Martin Kay make_table(Pattern) : retractall(border_table(_, _)), assert(border_table(0, 0)), assert(border_table(1, 0)), length(Pattern, PL), make_table(Pattern, 2, PL). make_table(_, I, N) : I>N, !. make_table(Pattern, I, N) : border(I, Pattern, K), assert(border_table(I, K)), J is I+1, make_table(Pattern, J, N). String Matching 1 25

Building A Table border(I, Pattern, Q) : J is I-1, border_table(J, P), nth 0(J, Pattern, C), extend(C, P, Pattern, Q). extend(_, -1, _, 0). extend(C, P, Pattern, Q) : nth 0(P, Pattern, C), !, Q is P+1. extend(C, P 0, Pattern, R) : border_table(P 0, Q), extend(C, Q, Pattern, R). Martin Kay make_table(Pattern) : retractall(border_table(_, _)), assert(border_table(0, 0)), assert(border_table(1, 0)), length(Pattern, PL), make_table(Pattern, 2, PL). make_table(_, I, N) : I>N, !. make_table(Pattern, I, N) : border(I, Pattern, K), assert(border_table(I, K)), J is I+1, make_table(Pattern, J, N). String Matching 1 26

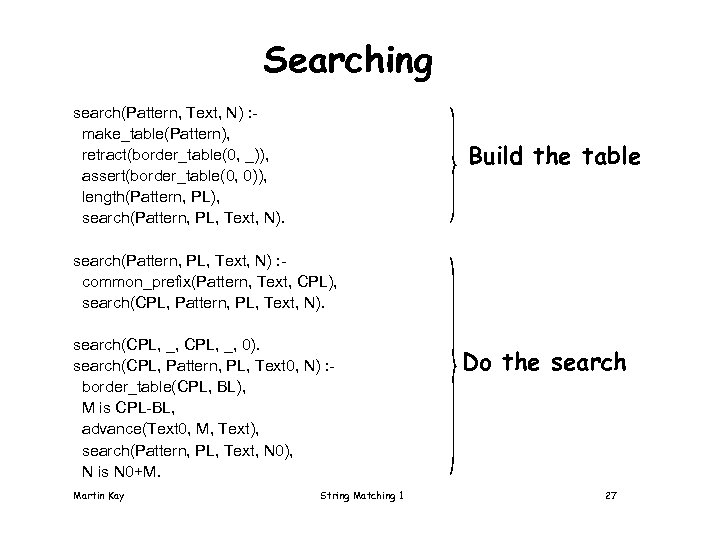Searching search(Pattern, Text, N) : make_table(Pattern), retract(border_table(0, _)), assert(border_table(0, 0)), length(Pattern, PL), search(Pattern, PL, Text, N). Build the table search(Pattern, PL, Text, N) : common_prefix(Pattern, Text, CPL), search(CPL, Pattern, PL, Text, N). search(CPL, _, 0). search(CPL, Pattern, PL, Text 0, N) : border_table(CPL, BL), M is CPL-BL, advance(Text 0, M, Text), search(Pattern, PL, Text, N 0), N is N 0+M. Martin Kay String Matching 1 Do the search 27

Reference Donald E. Knuth, James H. Morris, Jr. , and Vaughan R. Pratt. Fast pattern matching in strings. SIAM Journal on Computing , 6(2): 323 -350, June 1977. Martin Kay String Matching 1 28