7f8605ddfaaf6b049bc4479da49314b5.ppt
- Количество слайдов: 25

Markov Processes MBAP 6100 & EMEN 5600 Survey of Operations Research Professor Stephen Lawrence Leeds School of Business University of Colorado Boulder, CO 80309 -0419

OR Course Outline • • Intro to OR Linear Programming Solving LP’s LP Sensitivity/Duality Transport Problems Network Analysis Integer Programming • Nonlinear Programming • Dynamic Programming • Game Theory • Queueing Theory • Markov Processes • Decisions Analysis • Simulation
Whirlwind Tour of OR Markov Analysis Andrey A. Markov (born 1856). Early work in probability theory, proved central limit theorem

Agenda for This Week • Markov Processes – – – Stochastic processes Markov chains Future probabilities Steady state probabilities Markov chain concepts • Markov Applications – More Markov examples – Markov decision processes

Stochastic Processes • Series of random variables {Xt} • Series indexed over time interval T • Examples: X 1, X 2, … , Xt, … , XT represent – monthly inventory levels – daily closing price for a stock or index – availability of a new technology – market demand for a product

Markov Chains • Present state Xt is independent of history – previous states or events have no current or future influence on the current state • Process will move to other states with known transition probabilities • Transition probabilities are stationary – probabilities do not change over time • There exist a finite number of possible states

An Example of a Markov Chain A small community has two service stations: Petroco and Gasco. The marketing department of Petroco has found that customers switch between stations according to the following transition matrix: =1. 0 Note: Rows sum to 1. 0 !

Future State Probabilities Probability that a customer buying from Petroco this month will buy from Petroco next month: In two months: From Gasco in two months:
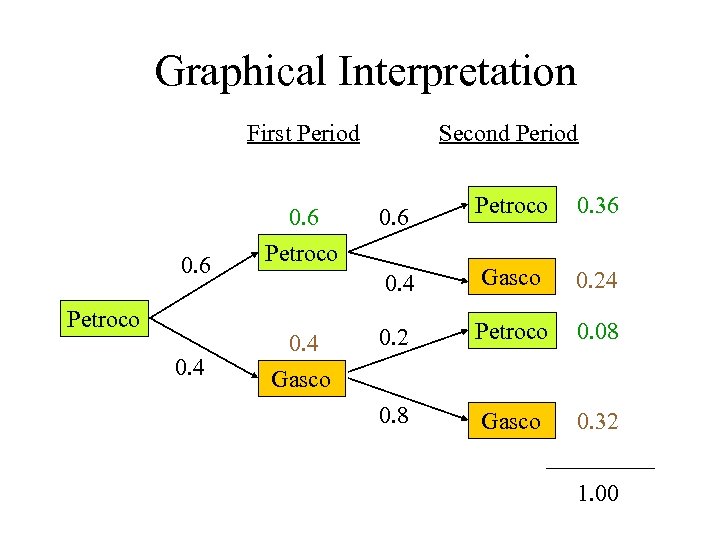
Graphical Interpretation First Period 0. 4 Gasco 0. 6 Petroco 0. 36 0. 4 0. 6 Petroco Second Period Gasco 0. 24 0. 2 Petroco 0. 08 0. 8 Gasco 0. 32 1. 00

Chapman-Kolmogorov Equations Let P be the transition matrix for a Markov process. Then the n-step transition probability matrices can be found from: P(2) = P·P P(3) = P·P·P

CK Equations for Example P(1) P(2)

Starting States In current month, if 70% of customers shop at Petroco and 30% at Gasco, what will be the mix in 2 months? P s = [0. 70 0. 30] sn = s 0 P(n) s 2 = [0. 7 0. 3] = [0. 39 0. 61]

CK Equations in Steady State P(1) P(2) P(9)
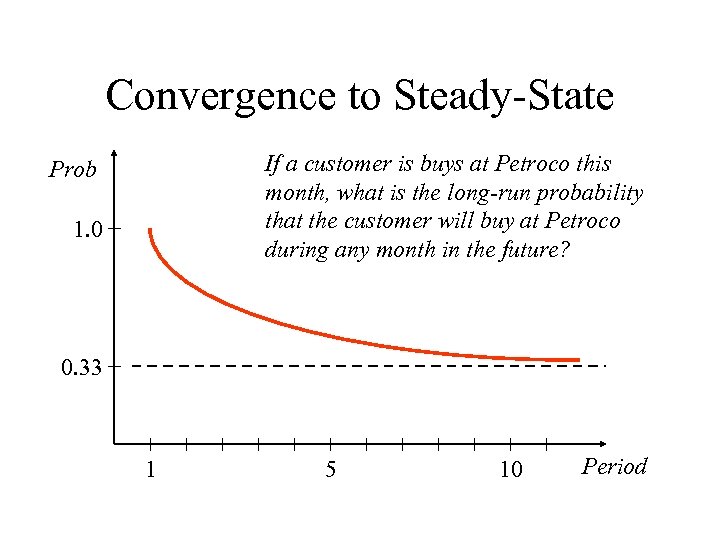
Convergence to Steady-State If a customer is buys at Petroco this month, what is the long-run probability that the customer will buy at Petroco during any month in the future? Prob 1. 0 0. 33 1 5 10 Period

Calculation of Steady State • Want outcome probabilities equal to incoming probabilities • Let s = [s 1, s 2, …, sn] be the vector of steadystate probabilities • Then we want s=s. P • That is, the output state probabilities do not change from transition to transition (e. g. , steady-state!)
![Steady-State for Example s=s. P P s = [p g] p = 0. 6 Steady-State for Example s=s. P P s = [p g] p = 0. 6](https://present5.com/presentation/7f8605ddfaaf6b049bc4479da49314b5/image-16.jpg)
Steady-State for Example s=s. P P s = [p g] p = 0. 6 p + 0. 2 g g = 0. 4 p + 0. 8 g p = 0. 333 g = 0. 667 p+g=1

Markov Chain Concepts • Steady-State Probabilities – long-run probability that a process starting in state i will be found in state j • First-Passage Time – length of time (steps) in going from state i to j • Recurrence Time – length of time (steps) to return to state i when starting in state i

Markov Chain Concepts (cont. ) • Accessible States – State j can be reached from i (pij(n) > 0) • Communicating States – State i and j are accessible from one another • Irreducible Markov chains – All states communicate with one another

Markov Chain Concepts (cont. ) • Recurrent State – A state that will certainly return to itself (fii = 1) • Transient State – A state that may return to itself (fii < 1) • Absorbing State – A state the never moves to another state (pii=1) – A “black hole”

Markov Examples Markov Decision Processes

Matrix Multiplication Matrix multiplication in Excel…

Machine Breakdown Example A critical machine in a manufacturing operation breaks down with some frequency. The hourly up-down transition matrix for the machine is shown below. What percentage of the time is the machine operating (up)? Up Down

Credit History Example The Rifle, CO Mercantile Department Store wants to analyze the payment behavior of customers who have outstanding accounts. The store’s credit department has determined the following bill payment pattern from historical records: Pay No Pay

Credit History Continued Further analysis reveals the following credit transition matrix at the Rifle Mercantile: 0 0 1 2 Pay Bad

University Graduation Example Fort Lewis College in Durango has determined that students progress through the college according to the following transition matrix: F F So J Sr D G
7f8605ddfaaf6b049bc4479da49314b5.ppt