d9a1f0a72245f414cfc9e4963c7416ad.ppt
- Количество слайдов: 54
 Markov Logic: A Representation Language for Natural Language Semantics Pedro Domingos Dept. Computer Science & Eng. University of Washington (Based on joint work with Stanley Kok, Matt Richardson and Parag Singla)
Markov Logic: A Representation Language for Natural Language Semantics Pedro Domingos Dept. Computer Science & Eng. University of Washington (Based on joint work with Stanley Kok, Matt Richardson and Parag Singla)
 Overview l l l l Motivation Background Representation Inference Learning Applications Discussion
Overview l l l l Motivation Background Representation Inference Learning Applications Discussion
 Motivation l Natural language is characterized by l l l Complex relational structure High uncertainty (ambiguity, imperfect knowledge) First-order logic handles relational structure Probability handles uncertainty Let’s combine the two
Motivation l Natural language is characterized by l l l Complex relational structure High uncertainty (ambiguity, imperfect knowledge) First-order logic handles relational structure Probability handles uncertainty Let’s combine the two
![Markov Logic [Richardson & Domingos, 2006] l l Syntax: First-order logic + Weights Semantics: Markov Logic [Richardson & Domingos, 2006] l l Syntax: First-order logic + Weights Semantics:](https://present5.com/presentation/d9a1f0a72245f414cfc9e4963c7416ad/image-4.jpg) Markov Logic [Richardson & Domingos, 2006] l l Syntax: First-order logic + Weights Semantics: Templates for Markov nets Inference: Weighted satisfiability + MCMC Learning: Voted perceptron + ILP
Markov Logic [Richardson & Domingos, 2006] l l Syntax: First-order logic + Weights Semantics: Templates for Markov nets Inference: Weighted satisfiability + MCMC Learning: Voted perceptron + ILP
 Overview l l l l Motivation Background Representation Inference Learning Applications Discussion
Overview l l l l Motivation Background Representation Inference Learning Applications Discussion
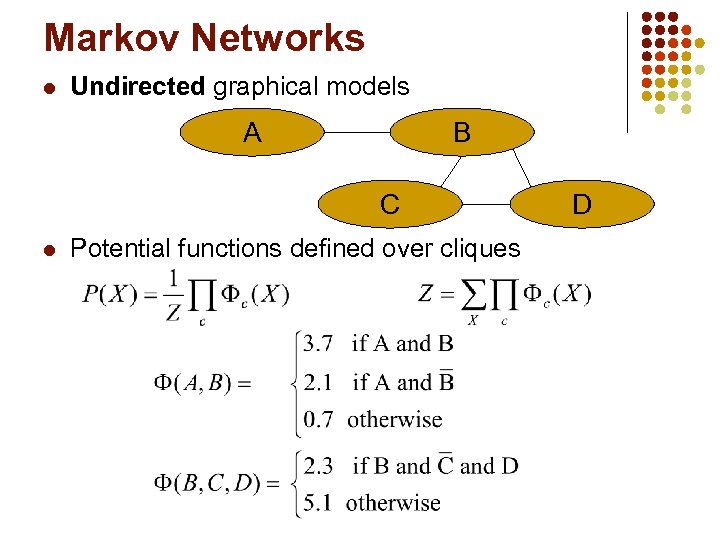 Markov Networks l Undirected graphical models A B C l Potential functions defined over cliques D
Markov Networks l Undirected graphical models A B C l Potential functions defined over cliques D
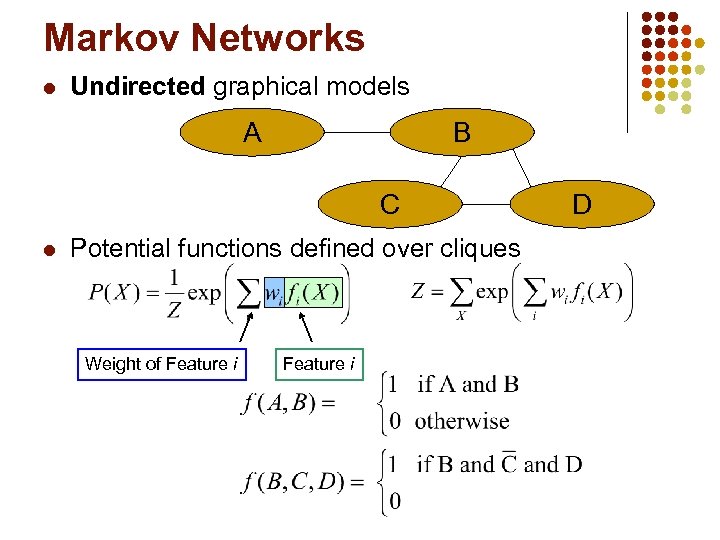 Markov Networks l Undirected graphical models A B C l Potential functions defined over cliques Weight of Feature i D
Markov Networks l Undirected graphical models A B C l Potential functions defined over cliques Weight of Feature i D
 First-Order Logic l l l Constants, variables, functions, predicates E. g. : Anna, X, mother_of(X), friends(X, Y) Grounding: Replace all variables by constants E. g. : friends (Anna, Bob) World (model, interpretation): Assignment of truth values to all ground predicates
First-Order Logic l l l Constants, variables, functions, predicates E. g. : Anna, X, mother_of(X), friends(X, Y) Grounding: Replace all variables by constants E. g. : friends (Anna, Bob) World (model, interpretation): Assignment of truth values to all ground predicates
 Overview l l l l Motivation Background Representation Inference Learning Applications Discussion
Overview l l l l Motivation Background Representation Inference Learning Applications Discussion
 Markov Logic Networks l l l A logical KB is a set of hard constraints on the set of possible worlds Let’s make them soft constraints: When a world violates a formula, It becomes less probable, not impossible Give each formula a weight (Higher weight Stronger constraint)
Markov Logic Networks l l l A logical KB is a set of hard constraints on the set of possible worlds Let’s make them soft constraints: When a world violates a formula, It becomes less probable, not impossible Give each formula a weight (Higher weight Stronger constraint)
 Definition l A Markov Logic Network (MLN) is a set of pairs (F, w) where l l l F is a formula in first-order logic w is a real number Together with a set of constants, it defines a Markov network with l l One node for each grounding of each predicate in the MLN One feature for each grounding of each formula F in the MLN, with the corresponding weight w
Definition l A Markov Logic Network (MLN) is a set of pairs (F, w) where l l l F is a formula in first-order logic w is a real number Together with a set of constants, it defines a Markov network with l l One node for each grounding of each predicate in the MLN One feature for each grounding of each formula F in the MLN, with the corresponding weight w
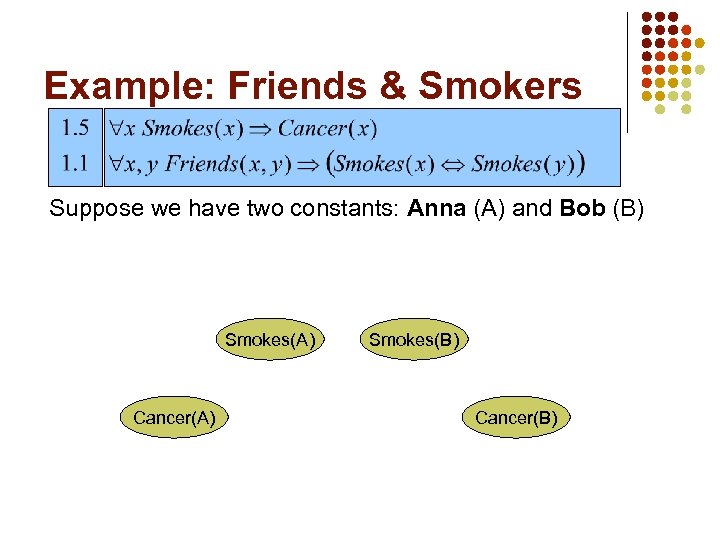 Example: Friends & Smokers Suppose we have two constants: Anna (A) and Bob (B) Smokes(A) Cancer(A) Smokes(B) Cancer(B)
Example: Friends & Smokers Suppose we have two constants: Anna (A) and Bob (B) Smokes(A) Cancer(A) Smokes(B) Cancer(B)
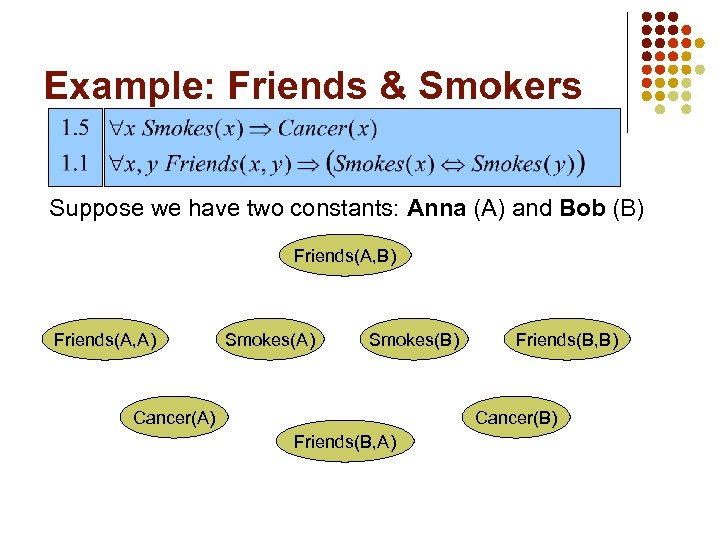 Example: Friends & Smokers Suppose we have two constants: Anna (A) and Bob (B) Friends(A, A) Smokes(B) Cancer(A) Friends(B, B) Cancer(B) Friends(B, A)
Example: Friends & Smokers Suppose we have two constants: Anna (A) and Bob (B) Friends(A, A) Smokes(B) Cancer(A) Friends(B, B) Cancer(B) Friends(B, A)
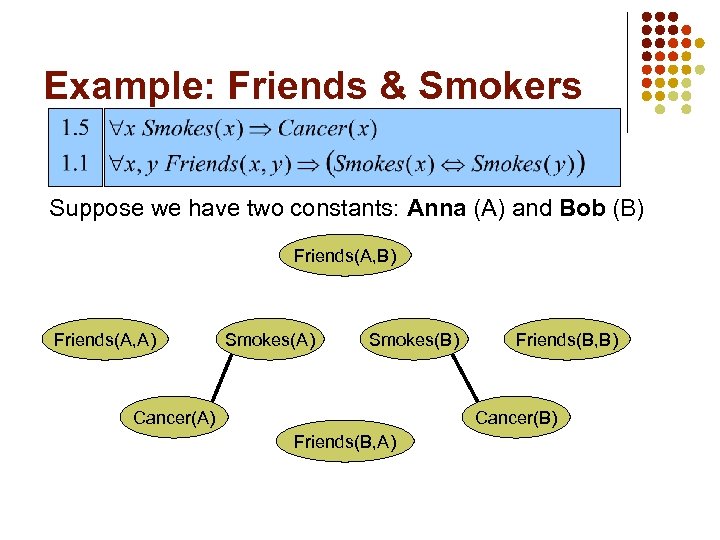 Example: Friends & Smokers Suppose we have two constants: Anna (A) and Bob (B) Friends(A, A) Smokes(B) Cancer(A) Friends(B, B) Cancer(B) Friends(B, A)
Example: Friends & Smokers Suppose we have two constants: Anna (A) and Bob (B) Friends(A, A) Smokes(B) Cancer(A) Friends(B, B) Cancer(B) Friends(B, A)
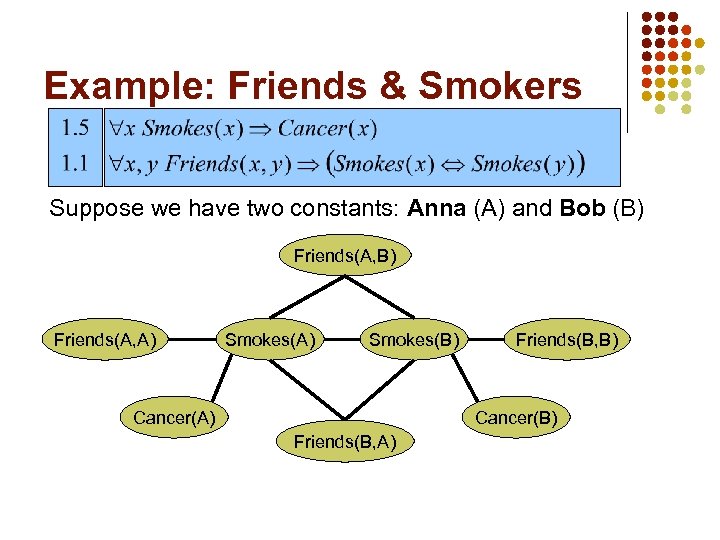 Example: Friends & Smokers Suppose we have two constants: Anna (A) and Bob (B) Friends(A, A) Smokes(B) Cancer(A) Friends(B, B) Cancer(B) Friends(B, A)
Example: Friends & Smokers Suppose we have two constants: Anna (A) and Bob (B) Friends(A, A) Smokes(B) Cancer(A) Friends(B, B) Cancer(B) Friends(B, A)
 More on MLNs l l MLN is template for ground Markov nets Typed variables and constants greatly reduce size of ground Markov net Functions, existential quantifiers, etc. MLN without variables = Markov network (subsumes graphical models)
More on MLNs l l MLN is template for ground Markov nets Typed variables and constants greatly reduce size of ground Markov net Functions, existential quantifiers, etc. MLN without variables = Markov network (subsumes graphical models)
 Relation to First-Order Logic l l l Infinite weights First-order logic Satisfiable KB, positive weights Satisfying assignments = Modes of distribution MLNs allow contradictions between formulas
Relation to First-Order Logic l l l Infinite weights First-order logic Satisfiable KB, positive weights Satisfying assignments = Modes of distribution MLNs allow contradictions between formulas
 Overview l l l l Motivation Background Representation Inference Learning Applications Discussion
Overview l l l l Motivation Background Representation Inference Learning Applications Discussion
 MPE/MAP Inference l l l Find most likely truth values of non-evidence ground atoms given evidence Apply weighted satisfiability solver (maxes sum of weights of satisfied clauses) Max. Walk. Sat algorithm [Kautz et al. , 1997] l l Start with random truth assignment With prob p, flip atom that maxes weight sum; else flip random atom in unsatisfied clause Repeat n times Restart m times
MPE/MAP Inference l l l Find most likely truth values of non-evidence ground atoms given evidence Apply weighted satisfiability solver (maxes sum of weights of satisfied clauses) Max. Walk. Sat algorithm [Kautz et al. , 1997] l l Start with random truth assignment With prob p, flip atom that maxes weight sum; else flip random atom in unsatisfied clause Repeat n times Restart m times
 Conditional Inference l l P(Formula|MLN, C) = ? MCMC: Sample worlds, check formula holds P(Formula 1|Formula 2, MLN, C) = ? If Formula 2 = Conjunction of ground atoms l l First construct min subset of network necessary to answer query (generalization of KBMC) Then apply MCMC (or other)
Conditional Inference l l P(Formula|MLN, C) = ? MCMC: Sample worlds, check formula holds P(Formula 1|Formula 2, MLN, C) = ? If Formula 2 = Conjunction of ground atoms l l First construct min subset of network necessary to answer query (generalization of KBMC) Then apply MCMC (or other)
 Ground Network Construction l l Initialize Markov net to contain all query preds For each node in network l l l Add node’s Markov blanket to network Remove any evidence nodes Repeat until done
Ground Network Construction l l Initialize Markov net to contain all query preds For each node in network l l l Add node’s Markov blanket to network Remove any evidence nodes Repeat until done
 Probabilistic Inference l Recall l l Exact inference is #P-complete Conditioning on Markov blanket is easy: l Gibbs sampling exploits this
Probabilistic Inference l Recall l l Exact inference is #P-complete Conditioning on Markov blanket is easy: l Gibbs sampling exploits this
 Markov Chain Monte Carlo l Gibbs Sampler 1. Start with an initial assignment to nodes 2. One node at a time, sample node given others 3. Repeat 4. Use samples to compute P(X) l l l Apply to ground network Initialization: Max. Walk. Sat Can use multiple chains
Markov Chain Monte Carlo l Gibbs Sampler 1. Start with an initial assignment to nodes 2. One node at a time, sample node given others 3. Repeat 4. Use samples to compute P(X) l l l Apply to ground network Initialization: Max. Walk. Sat Can use multiple chains
 Overview l l l l Motivation Background Representation Inference Learning Applications Discussion
Overview l l l l Motivation Background Representation Inference Learning Applications Discussion
 Learning l l l Data is a relational database Closed world assumption (if not: EM) Learning parameters (weights) l l l Generatively: Pseudo-likelihood Discriminatively: Voted perceptron + Max. Walk. Sat Learning structure l l l Generalization of feature induction in Markov nets Learn and/or modify clauses Inductive logic programming with pseudolikelihood as the objective function
Learning l l l Data is a relational database Closed world assumption (if not: EM) Learning parameters (weights) l l l Generatively: Pseudo-likelihood Discriminatively: Voted perceptron + Max. Walk. Sat Learning structure l l l Generalization of feature induction in Markov nets Learn and/or modify clauses Inductive logic programming with pseudolikelihood as the objective function
 Generative Weight Learning l l Maximize likelihood (or posterior) Use gradient ascent Feature count according to data Feature count according to model l Requires inference at each step (slow!)
Generative Weight Learning l l Maximize likelihood (or posterior) Use gradient ascent Feature count according to data Feature count according to model l Requires inference at each step (slow!)
![Pseudo-Likelihood [Besag, 1975] l l l Likelihood of each variable given its Markov blanket Pseudo-Likelihood [Besag, 1975] l l l Likelihood of each variable given its Markov blanket](https://present5.com/presentation/d9a1f0a72245f414cfc9e4963c7416ad/image-27.jpg) Pseudo-Likelihood [Besag, 1975] l l l Likelihood of each variable given its Markov blanket in the data Does not require inference at each step Widely used
Pseudo-Likelihood [Besag, 1975] l l l Likelihood of each variable given its Markov blanket in the data Does not require inference at each step Widely used
 Optimization l l Parameter tying over groundings of same clause Maximize using L-BFGS [Liu & Nocedal, 1989] where nsati(x=v) is the number of satisfied groundings of clause i in the training data when x takes value v l l Most terms not affected by changes in weights After initial setup, each iteration takes O(# ground predicates x # first-order clauses)
Optimization l l Parameter tying over groundings of same clause Maximize using L-BFGS [Liu & Nocedal, 1989] where nsati(x=v) is the number of satisfied groundings of clause i in the training data when x takes value v l l Most terms not affected by changes in weights After initial setup, each iteration takes O(# ground predicates x # first-order clauses)
 Discriminative Weight Learning Gradient of Conditional Log Likelihood # true groundings of formula in DB Expected # of true groundings – slow! Approximate expected count by MAP count
Discriminative Weight Learning Gradient of Conditional Log Likelihood # true groundings of formula in DB Expected # of true groundings – slow! Approximate expected count by MAP count
![Voted Perceptron [Collins, 2002] Ø Ø Used for discriminative training of HMMs Expected count Voted Perceptron [Collins, 2002] Ø Ø Used for discriminative training of HMMs Expected count](https://present5.com/presentation/d9a1f0a72245f414cfc9e4963c7416ad/image-30.jpg) Voted Perceptron [Collins, 2002] Ø Ø Used for discriminative training of HMMs Expected count in gradient approximated by count in MAP state found using Viterbi algorithm Weights averaged over all iterations initialize wi=0 for t=1 to T do find the MAP configuration using Viterbi wi, = * (training count – MAP count) end for
Voted Perceptron [Collins, 2002] Ø Ø Used for discriminative training of HMMs Expected count in gradient approximated by count in MAP state found using Viterbi algorithm Weights averaged over all iterations initialize wi=0 for t=1 to T do find the MAP configuration using Viterbi wi, = * (training count – MAP count) end for
![Voted Perceptron for MLNs [Singla & Domingos, 2004] Ø Ø HMM is special case Voted Perceptron for MLNs [Singla & Domingos, 2004] Ø Ø HMM is special case](https://present5.com/presentation/d9a1f0a72245f414cfc9e4963c7416ad/image-31.jpg) Voted Perceptron for MLNs [Singla & Domingos, 2004] Ø Ø HMM is special case of MLN Expected count in gradient approximated by count in MAP state found using Max. Walk. Sat Weights averaged over all iterations initialize wi=0 for t=1 to T do find the MAP configuration using Max. Walk. Sat wi, = * (training count – MAP count) end for
Voted Perceptron for MLNs [Singla & Domingos, 2004] Ø Ø HMM is special case of MLN Expected count in gradient approximated by count in MAP state found using Max. Walk. Sat Weights averaged over all iterations initialize wi=0 for t=1 to T do find the MAP configuration using Max. Walk. Sat wi, = * (training count – MAP count) end for
 Overview l l l l Motivation Background Representation Inference Learning Applications Discussion
Overview l l l l Motivation Background Representation Inference Learning Applications Discussion
 Applications to Date l l l Entity resolution (Cora, Bib. Serv) Information extraction for biology (won LLL-2005 competition) Probabilistic Cyc Link prediction Topic propagation in scientific communities Etc.
Applications to Date l l l Entity resolution (Cora, Bib. Serv) Information extraction for biology (won LLL-2005 competition) Probabilistic Cyc Link prediction Topic propagation in scientific communities Etc.
 Entity Resolution l l Most logical systems make unique names assumption What if we don’t? Equality predicate: Same(A, B), or A = B Equality axioms l l Reflexivity, symmetry, transitivity For every unary predicate P: x 1 = x 2 => (P(x 1) <=> P(x 2)) For every binary predicate R: x 1 = x 2 y 1 = y 2 => (R(x 1, y 1) <=> R(x 2, y 2)) Etc. l But in Markov logic these are soft and learnable Can also introduce reverse direction: l Surprisingly, this is all that’s needed l R(x 1, y 1) R(x 2, y 2) x 1 = x 2 => y 1 = y 2
Entity Resolution l l Most logical systems make unique names assumption What if we don’t? Equality predicate: Same(A, B), or A = B Equality axioms l l Reflexivity, symmetry, transitivity For every unary predicate P: x 1 = x 2 => (P(x 1) <=> P(x 2)) For every binary predicate R: x 1 = x 2 y 1 = y 2 => (R(x 1, y 1) <=> R(x 2, y 2)) Etc. l But in Markov logic these are soft and learnable Can also introduce reverse direction: l Surprisingly, this is all that’s needed l R(x 1, y 1) R(x 2, y 2) x 1 = x 2 => y 1 = y 2
 Example: Citation Matching
Example: Citation Matching
 Markov Logic Formulation: Predicates l l l Are two bibliography records the same? Same. Bib(b 1, b 2) Are two field values the same? Same. Author(a 1, a 2) Same. Title(t 1, t 2) Same. Venue(v 1, v 2) How similar are two field strings? Predicates for ranges of cosine TF-IDF score: Title. TFIDF. 0(t 1, t 2) is true iff TF-IDF(t 1, t 2)=0 Title. TFIDF. 2(a 1, a 2) is true iff 0
Markov Logic Formulation: Predicates l l l Are two bibliography records the same? Same. Bib(b 1, b 2) Are two field values the same? Same. Author(a 1, a 2) Same. Title(t 1, t 2) Same. Venue(v 1, v 2) How similar are two field strings? Predicates for ranges of cosine TF-IDF score: Title. TFIDF. 0(t 1, t 2) is true iff TF-IDF(t 1, t 2)=0 Title. TFIDF. 2(a 1, a 2) is true iff 0
 Markov Logic Formulation: Formulas l l l Unit clauses (defaults): ! Same. Bib(b 1, b 2) Two fields are same => Corresponding bib. records are same: Author(b 1, a 1) Author(b 2, a 2) Same. Author(a 1, a 2) => Same. Bib(b 1, b 2) Two bib. records are same => Corresponding fields are same: Author(b 1, a 1) Author(b 2, a 2) Same. Bib(b 1, b 2) => Same. Author(a 1, a 2) High similarity score => Two fields are same: Title. TFIDF. 8(t 1, t 2) =>Same. Title(t 1, t 2) Transitive closure (not incorporated in experiments): Same. Bib(b 1, b 2) Same. Bib(b 2, b 3) => Same. Bib(b 1, b 3) 25 predicates, 46 first-order clauses
Markov Logic Formulation: Formulas l l l Unit clauses (defaults): ! Same. Bib(b 1, b 2) Two fields are same => Corresponding bib. records are same: Author(b 1, a 1) Author(b 2, a 2) Same. Author(a 1, a 2) => Same. Bib(b 1, b 2) Two bib. records are same => Corresponding fields are same: Author(b 1, a 1) Author(b 2, a 2) Same. Bib(b 1, b 2) => Same. Author(a 1, a 2) High similarity score => Two fields are same: Title. TFIDF. 8(t 1, t 2) =>Same. Title(t 1, t 2) Transitive closure (not incorporated in experiments): Same. Bib(b 1, b 2) Same. Bib(b 2, b 3) => Same. Bib(b 1, b 3) 25 predicates, 46 first-order clauses
 What Does This Buy You? l l l Objects are matched collectively Multiple types matched simultaneously Constraints are soft, and strengths can be learned from data Easy to add further knowledge Constraints can be refined from data Standard approach still embedded
What Does This Buy You? l l l Objects are matched collectively Multiple types matched simultaneously Constraints are soft, and strengths can be learned from data Easy to add further knowledge Constraints can be refined from data Standard approach still embedded
 Example Record Title Author Venue B 1 Object Identification using CRFs Linda Stewart PKDD 04 B 2 Object Identification using CRFs Linda Stewart 8 th PKDD B 3 Learning Boolean Formulas Bill Johnson PKDD 04 B 4 Learning of Boolean Formulas William Johnson 8 th PKDD Subset of a Bibliography Database
Example Record Title Author Venue B 1 Object Identification using CRFs Linda Stewart PKDD 04 B 2 Object Identification using CRFs Linda Stewart 8 th PKDD B 3 Learning Boolean Formulas Bill Johnson PKDD 04 B 4 Learning of Boolean Formulas William Johnson 8 th PKDD Subset of a Bibliography Database
![Standard Approach [Fellegi & Sunter, 1969] Title Sim(Object Identification using CRFs, Object Identification using Standard Approach [Fellegi & Sunter, 1969] Title Sim(Object Identification using CRFs, Object Identification using](https://present5.com/presentation/d9a1f0a72245f414cfc9e4963c7416ad/image-40.jpg) Standard Approach [Fellegi & Sunter, 1969] Title Sim(Object Identification using CRFs, Object Identification using CRFs) Sim(Learning Boolean Formulas, Learning of Boolean Expressions) b 1=b 2 ? b 3=b 4 ? Sim(PKDD 04, 8 th PKDD) Sim(Linda Stewart, Linda Stewart) Venue Sim(PKDD 04, 8 th PKDD) Venue Author Sim(Bill Johnson, William Johnson) Author record-match node field-similarity node (evidence node)
Standard Approach [Fellegi & Sunter, 1969] Title Sim(Object Identification using CRFs, Object Identification using CRFs) Sim(Learning Boolean Formulas, Learning of Boolean Expressions) b 1=b 2 ? b 3=b 4 ? Sim(PKDD 04, 8 th PKDD) Sim(Linda Stewart, Linda Stewart) Venue Sim(PKDD 04, 8 th PKDD) Venue Author Sim(Bill Johnson, William Johnson) Author record-match node field-similarity node (evidence node)
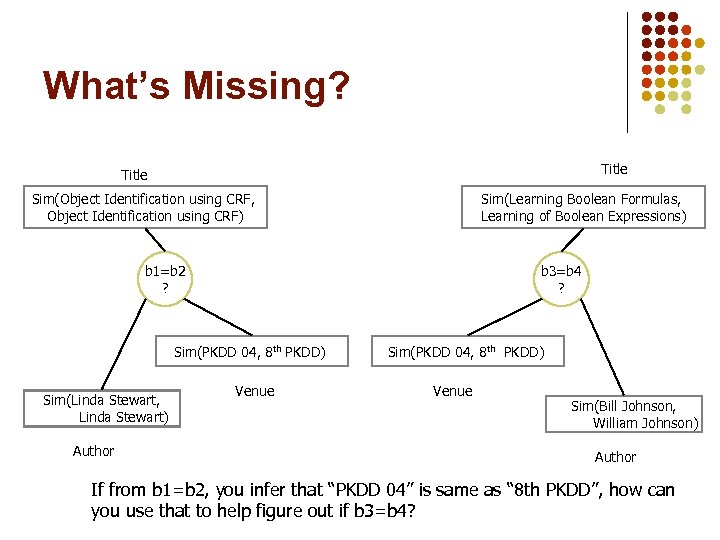 What’s Missing? Title Sim(Object Identification using CRF, Object Identification using CRF) Sim(Learning Boolean Formulas, Learning of Boolean Expressions) b 1=b 2 ? b 3=b 4 ? Sim(PKDD 04, 8 th PKDD) Sim(Linda Stewart, Linda Stewart) Author Venue Sim(PKDD 04, 8 th PKDD) Venue Sim(Bill Johnson, William Johnson) Author If from b 1=b 2, you infer that “PKDD 04” is same as “ 8 th PKDD”, how can you use that to help figure out if b 3=b 4?
What’s Missing? Title Sim(Object Identification using CRF, Object Identification using CRF) Sim(Learning Boolean Formulas, Learning of Boolean Expressions) b 1=b 2 ? b 3=b 4 ? Sim(PKDD 04, 8 th PKDD) Sim(Linda Stewart, Linda Stewart) Author Venue Sim(PKDD 04, 8 th PKDD) Venue Sim(Bill Johnson, William Johnson) Author If from b 1=b 2, you infer that “PKDD 04” is same as “ 8 th PKDD”, how can you use that to help figure out if b 3=b 4?
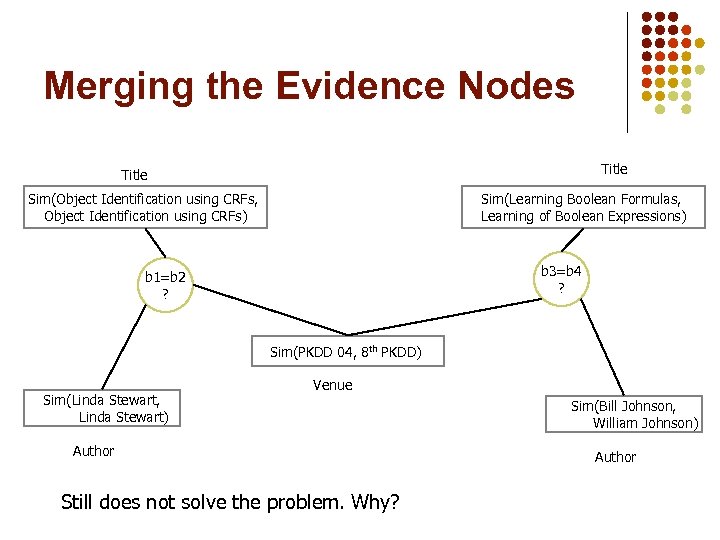 Merging the Evidence Nodes Title Sim(Object Identification using CRFs, Object Identification using CRFs) Sim(Learning Boolean Formulas, Learning of Boolean Expressions) b 3=b 4 ? b 1=b 2 ? Sim(PKDD 04, 8 th PKDD) Sim(Linda Stewart, Linda Stewart) Venue Author Still does not solve the problem. Why? Sim(Bill Johnson, William Johnson) Author
Merging the Evidence Nodes Title Sim(Object Identification using CRFs, Object Identification using CRFs) Sim(Learning Boolean Formulas, Learning of Boolean Expressions) b 3=b 4 ? b 1=b 2 ? Sim(PKDD 04, 8 th PKDD) Sim(Linda Stewart, Linda Stewart) Venue Author Still does not solve the problem. Why? Sim(Bill Johnson, William Johnson) Author
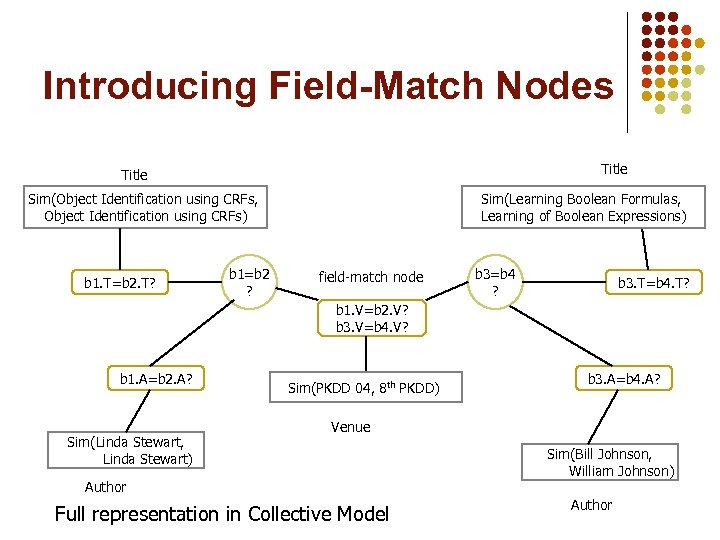 Introducing Field-Match Nodes Title Sim(Object Identification using CRFs, Object Identification using CRFs) b 1. T=b 2. T? b 1=b 2 ? Sim(Learning Boolean Formulas, Learning of Boolean Expressions) field-match node b 3=b 4 ? b 3. T=b 4. T? b 1. V=b 2. V? b 3. V=b 4. V? b 1. A=b 2. A? Sim(Linda Stewart, Linda Stewart) Sim(PKDD 04, 8 th PKDD) b 3. A=b 4. A? Venue Author Full representation in Collective Model Sim(Bill Johnson, William Johnson) Author
Introducing Field-Match Nodes Title Sim(Object Identification using CRFs, Object Identification using CRFs) b 1. T=b 2. T? b 1=b 2 ? Sim(Learning Boolean Formulas, Learning of Boolean Expressions) field-match node b 3=b 4 ? b 3. T=b 4. T? b 1. V=b 2. V? b 3. V=b 4. V? b 1. A=b 2. A? Sim(Linda Stewart, Linda Stewart) Sim(PKDD 04, 8 th PKDD) b 3. A=b 4. A? Venue Author Full representation in Collective Model Sim(Bill Johnson, William Johnson) Author
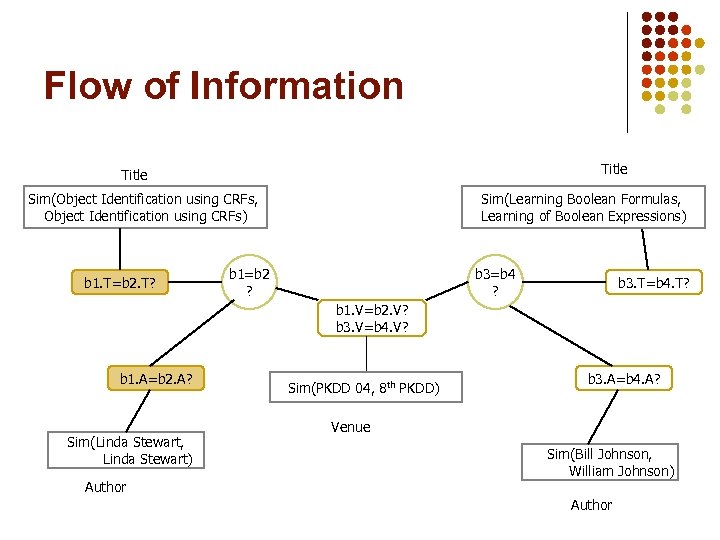 Flow of Information Title Sim(Object Identification using CRFs, Object Identification using CRFs) b 1. T=b 2. T? Sim(Learning Boolean Formulas, Learning of Boolean Expressions) b 1=b 2 ? b 3=b 4 ? b 3. T=b 4. T? b 1. V=b 2. V? b 3. V=b 4. V? b 1. A=b 2. A? Sim(Linda Stewart, Linda Stewart) Author Sim(PKDD 04, 8 th PKDD) b 3. A=b 4. A? Venue Sim(Bill Johnson, William Johnson) Author
Flow of Information Title Sim(Object Identification using CRFs, Object Identification using CRFs) b 1. T=b 2. T? Sim(Learning Boolean Formulas, Learning of Boolean Expressions) b 1=b 2 ? b 3=b 4 ? b 3. T=b 4. T? b 1. V=b 2. V? b 3. V=b 4. V? b 1. A=b 2. A? Sim(Linda Stewart, Linda Stewart) Author Sim(PKDD 04, 8 th PKDD) b 3. A=b 4. A? Venue Sim(Bill Johnson, William Johnson) Author
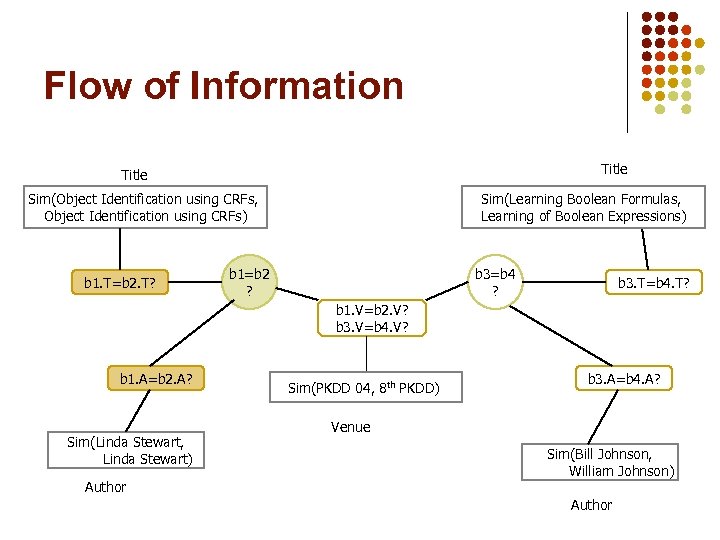 Flow of Information Title Sim(Object Identification using CRFs, Object Identification using CRFs) b 1. T=b 2. T? Sim(Learning Boolean Formulas, Learning of Boolean Expressions) b 1=b 2 ? b 3=b 4 ? b 3. T=b 4. T? b 1. V=b 2. V? b 3. V=b 4. V? b 1. A=b 2. A? Sim(Linda Stewart, Linda Stewart) Author Sim(PKDD 04, 8 th PKDD) b 3. A=b 4. A? Venue Sim(Bill Johnson, William Johnson) Author
Flow of Information Title Sim(Object Identification using CRFs, Object Identification using CRFs) b 1. T=b 2. T? Sim(Learning Boolean Formulas, Learning of Boolean Expressions) b 1=b 2 ? b 3=b 4 ? b 3. T=b 4. T? b 1. V=b 2. V? b 3. V=b 4. V? b 1. A=b 2. A? Sim(Linda Stewart, Linda Stewart) Author Sim(PKDD 04, 8 th PKDD) b 3. A=b 4. A? Venue Sim(Bill Johnson, William Johnson) Author
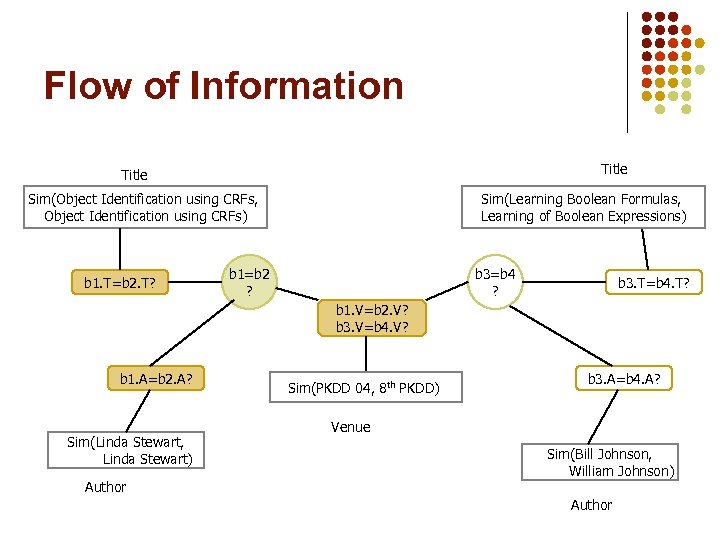 Flow of Information Title Sim(Object Identification using CRFs, Object Identification using CRFs) b 1. T=b 2. T? Sim(Learning Boolean Formulas, Learning of Boolean Expressions) b 1=b 2 ? b 3=b 4 ? b 3. T=b 4. T? b 1. V=b 2. V? b 3. V=b 4. V? b 1. A=b 2. A? Sim(Linda Stewart, Linda Stewart) Author Sim(PKDD 04, 8 th PKDD) b 3. A=b 4. A? Venue Sim(Bill Johnson, William Johnson) Author
Flow of Information Title Sim(Object Identification using CRFs, Object Identification using CRFs) b 1. T=b 2. T? Sim(Learning Boolean Formulas, Learning of Boolean Expressions) b 1=b 2 ? b 3=b 4 ? b 3. T=b 4. T? b 1. V=b 2. V? b 3. V=b 4. V? b 1. A=b 2. A? Sim(Linda Stewart, Linda Stewart) Author Sim(PKDD 04, 8 th PKDD) b 3. A=b 4. A? Venue Sim(Bill Johnson, William Johnson) Author
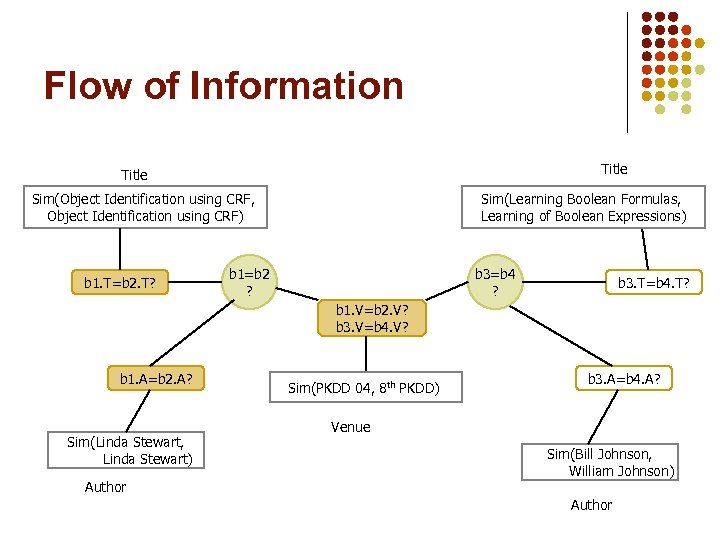 Flow of Information Title Sim(Object Identification using CRF, Object Identification using CRF) b 1. T=b 2. T? Sim(Learning Boolean Formulas, Learning of Boolean Expressions) b 1=b 2 ? b 3=b 4 ? b 3. T=b 4. T? b 1. V=b 2. V? b 3. V=b 4. V? b 1. A=b 2. A? Sim(Linda Stewart, Linda Stewart) Author Sim(PKDD 04, 8 th PKDD) b 3. A=b 4. A? Venue Sim(Bill Johnson, William Johnson) Author
Flow of Information Title Sim(Object Identification using CRF, Object Identification using CRF) b 1. T=b 2. T? Sim(Learning Boolean Formulas, Learning of Boolean Expressions) b 1=b 2 ? b 3=b 4 ? b 3. T=b 4. T? b 1. V=b 2. V? b 3. V=b 4. V? b 1. A=b 2. A? Sim(Linda Stewart, Linda Stewart) Author Sim(PKDD 04, 8 th PKDD) b 3. A=b 4. A? Venue Sim(Bill Johnson, William Johnson) Author
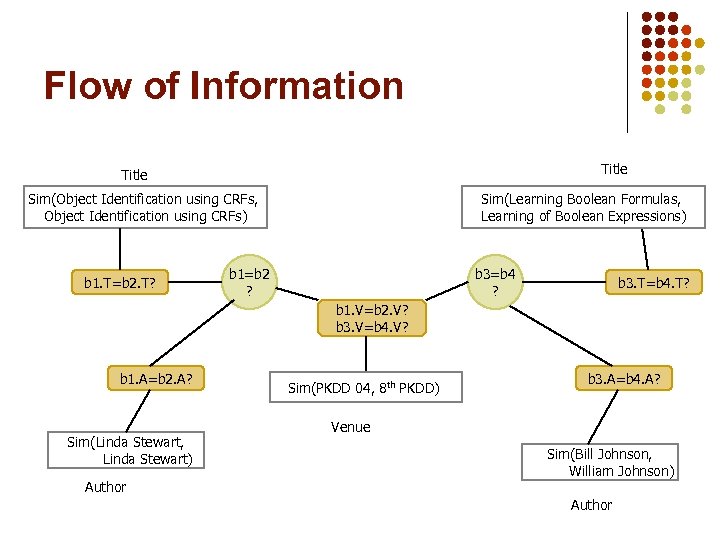 Flow of Information Title Sim(Object Identification using CRFs, Object Identification using CRFs) b 1. T=b 2. T? Sim(Learning Boolean Formulas, Learning of Boolean Expressions) b 1=b 2 ? b 3=b 4 ? b 3. T=b 4. T? b 1. V=b 2. V? b 3. V=b 4. V? b 1. A=b 2. A? Sim(Linda Stewart, Linda Stewart) Author Sim(PKDD 04, 8 th PKDD) b 3. A=b 4. A? Venue Sim(Bill Johnson, William Johnson) Author
Flow of Information Title Sim(Object Identification using CRFs, Object Identification using CRFs) b 1. T=b 2. T? Sim(Learning Boolean Formulas, Learning of Boolean Expressions) b 1=b 2 ? b 3=b 4 ? b 3. T=b 4. T? b 1. V=b 2. V? b 3. V=b 4. V? b 1. A=b 2. A? Sim(Linda Stewart, Linda Stewart) Author Sim(PKDD 04, 8 th PKDD) b 3. A=b 4. A? Venue Sim(Bill Johnson, William Johnson) Author
 Experiments l Databases: l l l l Cora [Mc. Callum et al. , IRJ, 2000]: 1295 records, 132 papers Bib. Serv. org [Richardson & Domingos, ISWC-03]: 21, 805 records, unknown #papers Goal: De-duplicate bib. records, authors and venues Pre-processing: Form canopies [Mc. Callum et al, KDD-00 ] Compared with naïve Bayes (standard method), etc. Measured area under precision-recall curve (AUC) Our approach wins across the board
Experiments l Databases: l l l l Cora [Mc. Callum et al. , IRJ, 2000]: 1295 records, 132 papers Bib. Serv. org [Richardson & Domingos, ISWC-03]: 21, 805 records, unknown #papers Goal: De-duplicate bib. records, authors and venues Pre-processing: Form canopies [Mc. Callum et al, KDD-00 ] Compared with naïve Bayes (standard method), etc. Measured area under precision-recall curve (AUC) Our approach wins across the board
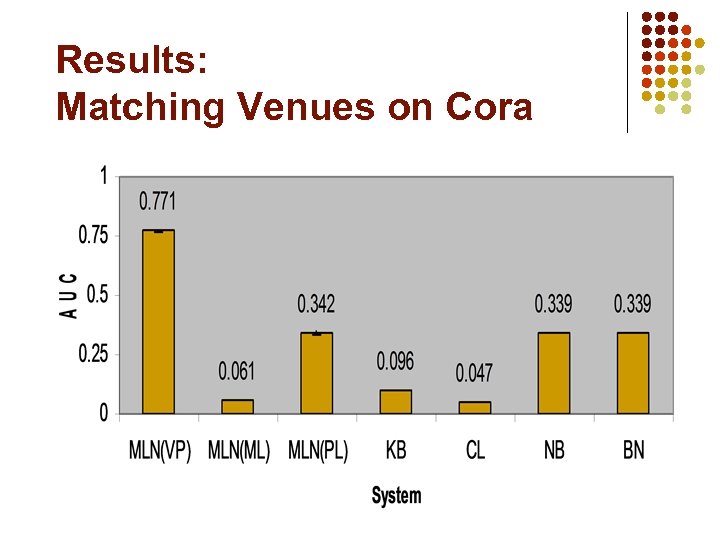 Results: Matching Venues on Cora
Results: Matching Venues on Cora
 Overview l l l l Motivation Background Representation Inference Learning Applications Discussion
Overview l l l l Motivation Background Representation Inference Learning Applications Discussion
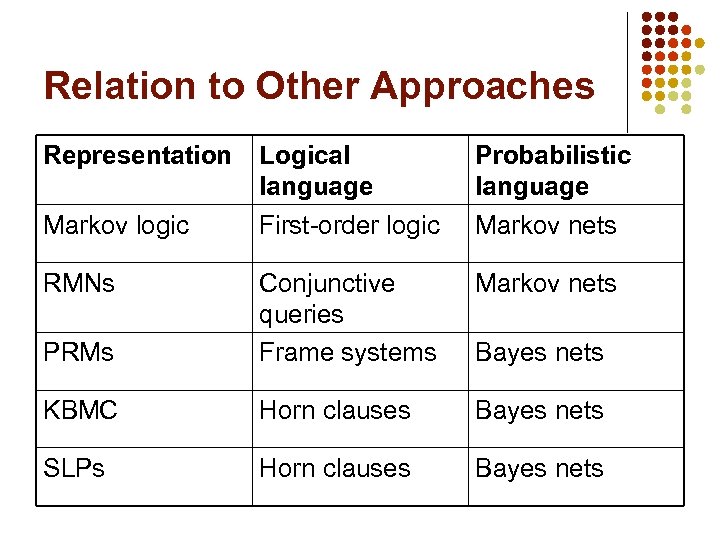 Relation to Other Approaches Representation Logical language First-order logic Probabilistic language Markov nets PRMs Conjunctive queries Frame systems KBMC Horn clauses Bayes nets SLPs Horn clauses Bayes nets Markov logic RMNs Bayes nets
Relation to Other Approaches Representation Logical language First-order logic Probabilistic language Markov nets PRMs Conjunctive queries Frame systems KBMC Horn clauses Bayes nets SLPs Horn clauses Bayes nets Markov logic RMNs Bayes nets
 Going Further l l l First-order logic is not enough We can “Markovize” other representations in the same way Lots to do
Going Further l l l First-order logic is not enough We can “Markovize” other representations in the same way Lots to do
 Summary l l NLP involves relational structure, uncertainty Markov logic combines first-order logic and probabilistic graphical models l l l Syntax: First-order logic + Weights Semantics: Templates for Markov networks Inference: Max. Walk. Sat + KBMC + MCMC Learning: Voted perceptron + PL + ILP Applications to date: Entity resolution, IE, etc. Software: Alchemy http: //www. cs. washington. edu/ai/alchemy
Summary l l NLP involves relational structure, uncertainty Markov logic combines first-order logic and probabilistic graphical models l l l Syntax: First-order logic + Weights Semantics: Templates for Markov networks Inference: Max. Walk. Sat + KBMC + MCMC Learning: Voted perceptron + PL + ILP Applications to date: Entity resolution, IE, etc. Software: Alchemy http: //www. cs. washington. edu/ai/alchemy


