Market Equilibrium and Algorithmic Game Theory Pricing of

Market Equilibrium and Algorithmic Game Theory Pricing of Goods and Internet Computing Vijay V. Vazirani Georgia Tech

Adam Smith n The Wealth of Nations, 1776. “It is not from the benevolence of the butcher, the brewer, or the baker, that we expect our dinner, but from their regard for their own interest. ” Each participant in a competitive economy is “led by an invisible hand to promote an end which was no part of his intention. ”

What is Economics? ‘‘Economics is the study of the use of scarce resources which have alternative uses. ’’ Lionel Robbins (1898 – 1984)

How are scarce resources assigned to alternative uses?

How are scarce resources assigned to alternative uses? Prices!

How are scarce resources assigned to alternative uses? Prices Parity between demand supply

How are scarce resources assigned to alternative uses? Prices Parity between demand supply equilibrium prices

Leon Walras, 1874 n Pioneered general equilibrium theory

General Equilibrium Theory Occupied center stage in Mathematical Economics for over a century Mathematical ratification!

Central tenet n Markets should operate at equilibrium

Central tenet n Markets should operate at equilibrium i. e. , prices s. t. Parity between supply and demand

Do markets even admit equilibrium prices?

Do markets even admit equilibrium prices? Easy if only one good!

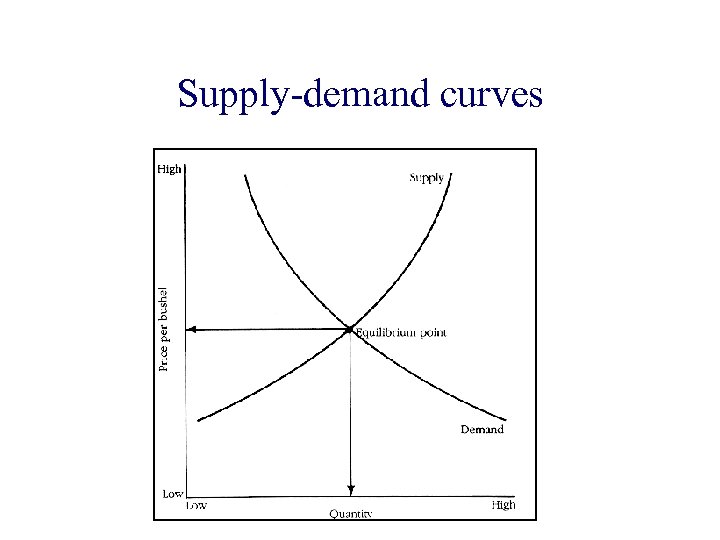
Supply-demand curves

Do markets even admit equilibrium prices? What if there are multiple goods and multiple buyers with diverse desires and different buying power?

Irving Fisher, 1891 n Defined a fundamental market model n Special case of Walras’ model

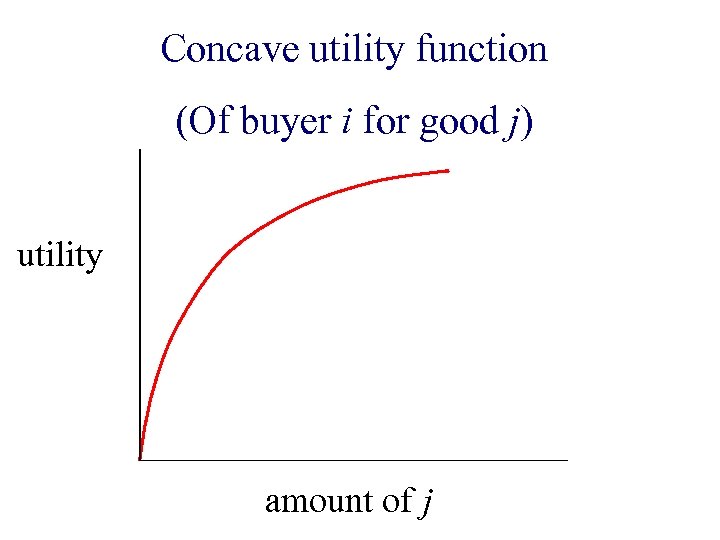
Concave utility function (Of buyer i for good j) utility amount of j

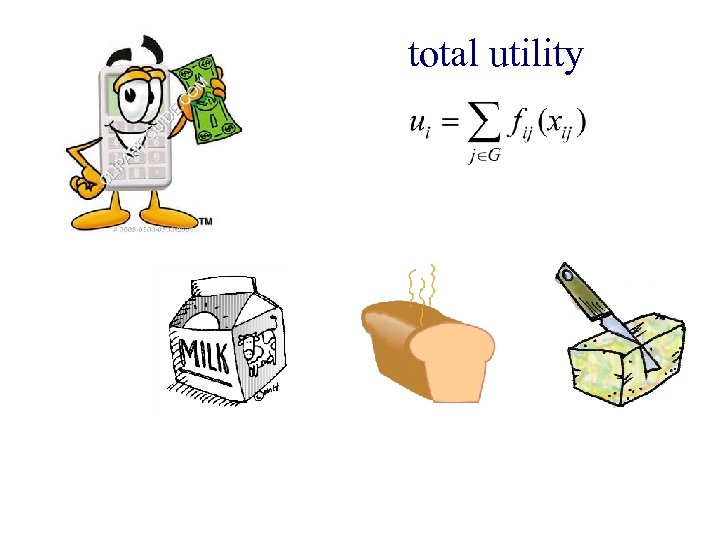
total utility

For given prices, find optimal bundle of goods

Several buyers with different utility functions and moneys.

Several buyers with different utility functions and moneys. Equilibrium prices

Several buyers with different utility functions and moneys. Show equilibrium prices exist.

Arrow-Debreu Theorem, 1954 n Celebrated theorem in Mathematical Economics n Established existence of market equilibrium under very general conditions using a deep theorem from topology - Kakutani fixed point theorem.

First Welfare Theorem n Competitive equilibrium => Pareto optimal allocation of resources n Pareto optimal = impossible to make an agent better off without making some other agent worse off

Second Welfare Theorem n Every Pareto optimal allocation of resources comes from a competitive equilibrium (after redistribution of initial endowments).

Kenneth Arrow n Nobel Prize, 1972

Gerard Debreu n Nobel Prize, 1983

Arrow-Debreu Model Agents: buyers/sellers

Initial endowment of goods Agents Goods

Prices = $25 = $10 Agents Goods

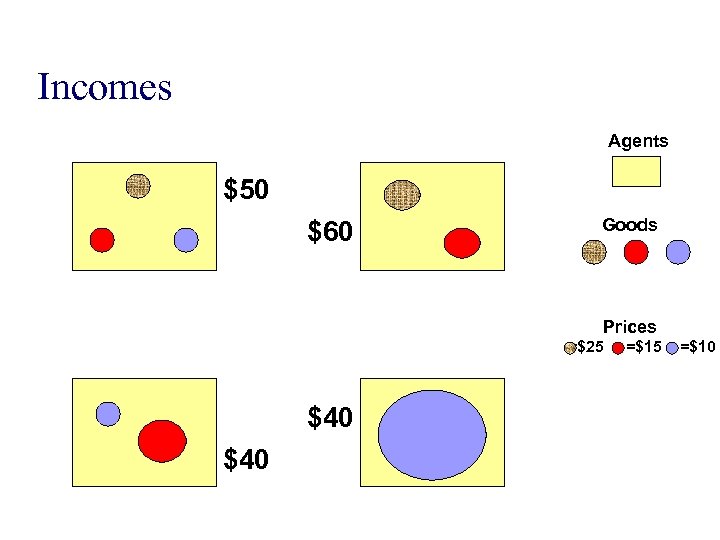
Incomes Agents $50 $60 Goods Prices =$25 $40 =$15 =$10

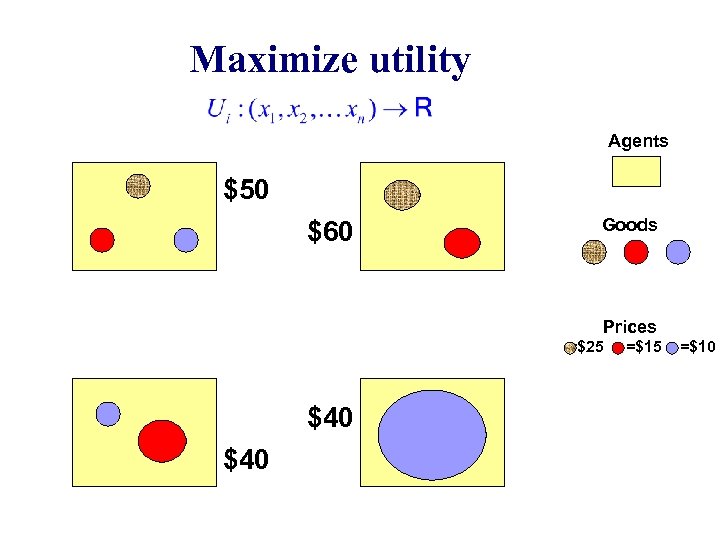
Maximize utility Agents $50 $60 Goods Prices =$25 $40 =$15 =$10

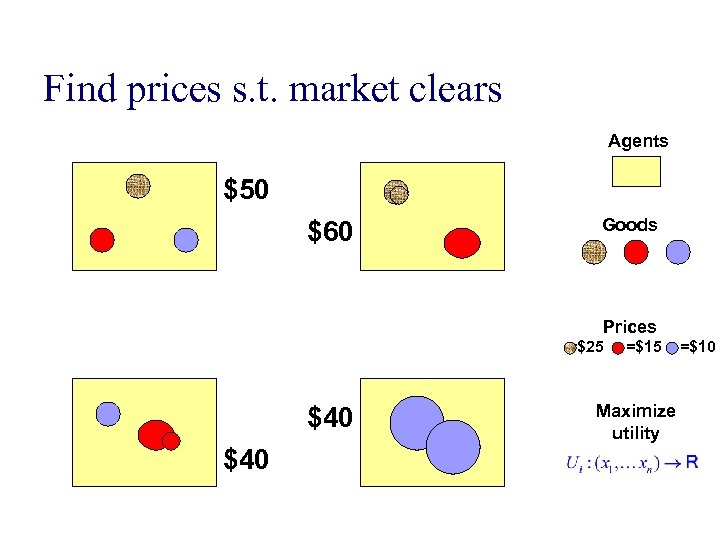
Find prices s. t. market clears Agents $50 $60 Goods Prices =$25 $40 =$15 Maximize utility =$10

Arrow-Debreu Model n n agents, k goods

Arrow-Debreu Model n n agents, k goods n Each agent has: initial endowment of goods, & a utility function

Arrow-Debreu Model n n agents, k goods Each agent has: initial endowment of goods, & a utility function n Find market clearing prices, i. e. , prices s. t. if n ¨ Each agent sells all her goods ¨ Buys optimal bundle using this money ¨ No surplus or deficiency of any good

Utility function of agent i n n Continuous, quasi-concave and satisfying non-satiation. n Given prices and money m, there is a unique utility maximizing bundle.

Proof of Arrow-Debreu Theorem n Uses Kakutani’s Fixed Point Theorem. ¨ Deep theorem in topology

Proof n Uses Kakutani’s Fixed Point Theorem. ¨ Deep n theorem in topology Will illustrate main idea via Brouwer’s Fixed Point Theorem (buggy proof!!)

Brouwer’s Fixed Point Theorem n Let be a non-empty, compact, convex set n Continuous function n Then

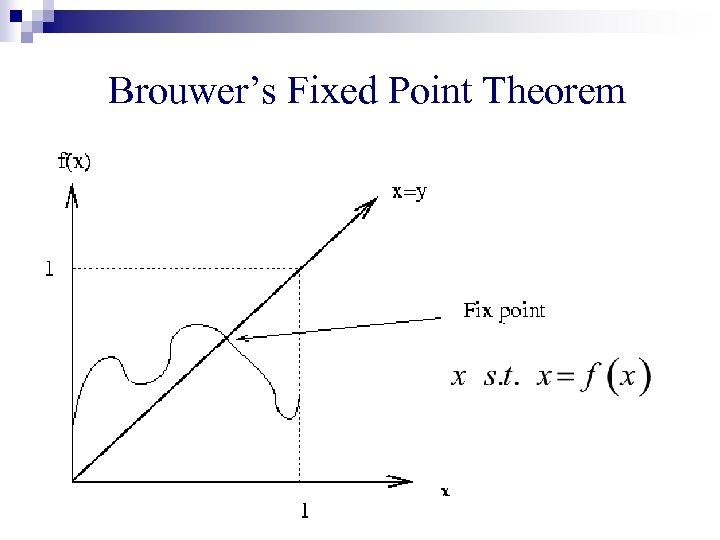
Brouwer’s Fixed Point Theorem

n n n Observe: If p is market clearing prices, then so is any scaling of p Assume w. l. o. g. that sum of prices of k goods is 1. k-1 dimensional unit simplex

Idea of proof n Will define continuous function n If p is not market clearing, f(p) tries to ‘correct’ this. n Therefore fixed points of f must be equilibrium prices.

When is p an equilibrium price? n s(j): total supply of good j. n B(i): unique optimal bundle which agent i wants to buy after selling her initial endowment at prices p. n d(j): total demand of good j.

When is p an equilibrium price? n s(j): total supply of good j. n B(i): unique optimal bundle which agent i wants to buy after selling her initial endowment at prices p. n d(j): total demand of good j. n For each good j: s(j) = d(j).

What if p is not an equilibrium price? n s(j) < d(j) => p(j) n s(j) > d(j) => p(j) n Also ensure

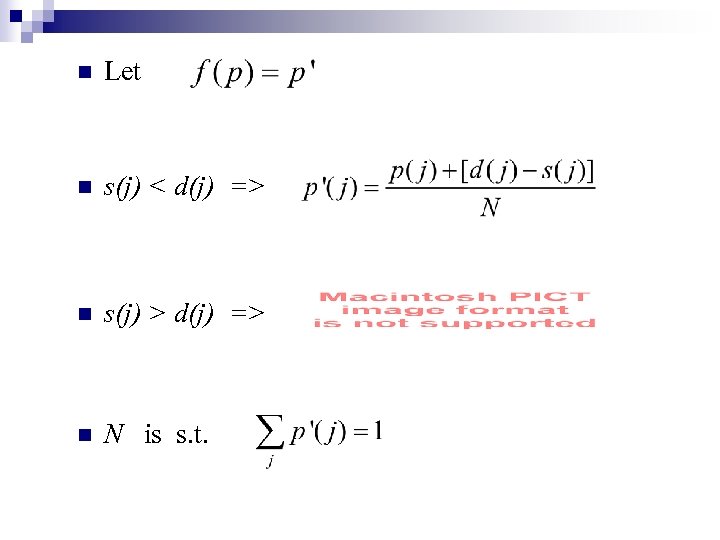
n Let n s(j) < d(j) => n s(j) > d(j) => n N is s. t.

is a cts. fn. => is a cts. fn. of p => f is a cts. fn. of p

is a cts. fn. => is a cts. fn. of p => f is a cts. fn. of p By Brouwer’s Theorem, equilibrium prices exist.

is a cts. fn. => is a cts. fn. of p => f is a cts. fn. of p By Brouwer’s Theorem, equilibrium prices exist. q. e. d. !

Bug? ?

n Boundaries of

n Boundaries of n B(i) is not defined at boundaries!!

Kakutani’s fixed point theorem n S: compact, convex set in upper hemi-continuous

Fisher reduces to Arrow-Debreu n Fisher: n buyers, k goods n AD: ¨ first n +1 agents n have money, utility for goods ¨ last agent has all goods, utility for money only.

Pricing of Digital Goods n Music, movies, video games, … cell phone apps. , …, web search results, … , even ideas!

Pricing of Digital Goods n Music, movies, video games, … cell phone apps. , …, web search results, … , even ideas! n Once produced, supply is infinite!!

What is Economics? ‘‘Economics is the study of the use of scarce resources which have alternative uses. ’’ Lionel Robbins (1898 – 1984)

Jain & V. , 2010: n Market model for digital goods, with notion of equilibrium. n Proof of existence of equilibrium.

Idiosyncrasies of Digital Realm n Staggering number of goods available with great ease, e. g. , i. Tunes has 11 million songs! n Once produced, infinite supply. n Want 2 songs => want 2 different songs, not 2 copies of same song. n Agents’ rating of songs varies widely.

Game-Theoretic Assumptions n Full rationality, infinite computing power: not meaningful!

Game-Theoretic Assumptions n Full rationality, infinite computing power: not meaningful! n e. g. , song A for $1. 23, song B for $1. 56, …

Game-Theoretic Assumptions n Full rationality, infinite computing power: not meaningful! n e. g. , song A for $1. 23, song B for $1. 56, … n Cannot price songs individually!

Market Model n Uniform pricing of all goods in a category. ¨ Assume n g categories of digital goods. Each agent has a total order over all songs in a category.

Arrow-Debreu-Based Market Model n Assume 1 conventional good: bread. n Each agent has a utility function over g digital categories and bread.

Optimal bundle for i, given prices p n First, compute i’s optimal bundle, i. e. , #songs from each digital category and no. of units of bread. n Next, from each digital category, i picks her most favorite songs.

Agents are also producers n Feasible production of each agent is a convex, compact set in n Agent’s earning: ¨ no. of units of bread produced ¨ no. of copies of each song sold n Agent spends earnings on optimal bundle.

Equilibrium (p, x, y) s. t. Each agent, i, gets optimal bundle & “best” songs in each category. n Each agent, k, maximizes earnings, given p, x, y(-k) n Market clears, i. e. , all bread sold & at least 1 copy of each song sold. n

Theorem (Jain & V. , 2010): Equilibrium exists. (Using Kakutani’s fixed-point theorem)

Arrow-Debreu Theorem, 1954 n Celebrated theorem in Mathematical Economics n Established existence of market equilibrium under very general conditions using a theorem from topology - Kakutani fixed point theorem. n Highly non-constructive!

Leon Walras n Tatonnement process: Price adjustment process to arrive at equilibrium ¨ Deficient goods: raise prices ¨ Excess goods: lower prices

Leon Walras n Tatonnement process: Price adjustment process to arrive at equilibrium ¨ Deficient goods: raise prices ¨ Excess goods: lower prices n Does it converge to equilibrium?

GETTING TO ECONOMIC EQUILIBRIUM: A PROBLEM AND ITS HISTORY For the third International Workshop on Internet and Network Economics Kenneth J. Arrow

OUTLINE I. III. IV. V. VI. BEFORE THE FORMULATION OF GENERAL EQUILIBRIUM THEORY PARTIAL EQUILIBRIUM WALRAS, PARETO, AND HICKS SOCIALISM AND DECENTRALIZATION SAMUELSON AND SUCCESSORS THE END OF THE PROGRAM

Part VI: THE END OF THE PROGRAM A. B. C. D. Scarf’s example Saari-Simon Theorem: For any dynamic system depending on first-order information (z) only, there is a set of excess demand functions for which stability fails. (In fact, theorem is stronger). Uzawa: Existence of general equilibrium is equivalent to fixed-point theorem Assumptions on individual demand functions do not constrain aggregate demand function (Sonnenschein, Debreu, Mantel)

Several buyers with different utility functions and moneys. Find equilibrium prices!!

The new face of computing

Today’s reality n New markets defined by Internet companies, e. g. , ¨ Microsoft ¨ Google ¨ e. Bay ¨ Yahoo! ¨ Amazon n Massive computing power available. n Need an inherently-algorithmic theory of markets and market equilibria.

Standard sufficient conditions on utility functions (in Arrow-Debreu Theorem): n Continuous, quasiconcave, satisfying non-satiation.

Complexity-theoretic question n For “reasonable” utility fns. , can market equilibrium be computed in P? n If not, what is its complexity?

Several buyers with different utility functions and moneys. Find equilibrium prices.

“Stock prices have reached what looks like a permanently high plateau”

“Stock prices have reached what looks like a permanently high plateau” Irving Fisher, October 1929

Linear Fisher Market n Assume: ¨ Buyer i’s total utility, mi : money of buyer i. ¨ One unit of each good j. ¨

Eisenberg-Gale Program, 1959

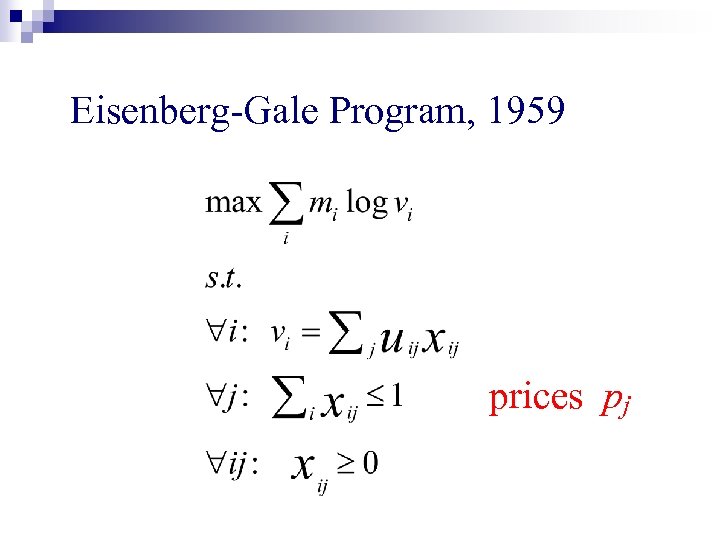
Eisenberg-Gale Program, 1959 prices pj

Why remarkable? n Equilibrium simultaneously optimizes for all agents. n How is this done via a single objective function?

Rational convex program n Always has a rational solution, using polynomially many bits, if all parameters are rational. n Eisenberg-Gale program is rational.

KKT Conditions n Generalization of complementary slackness conditions to convex programs. n Help prove optimal solution to EG program: ¨ Gives market equilibrium ¨ Is rational

Lagrange relaxation technique n Take constraints into objective with a penalty n Yields dual LP.