March 2010 doc IEEE 802 15 -10

March, 2010 doc. : IEEE 802. 15 -10 -0192 -03 -004 f Project: IEEE P 802. 15 Working Group for Wireless Personal Area Networks (WPANs) Submission Title: Integration lengths for long-range PHY Date Submitted: 16 th March 2010 Source: Andy Ward, Ubisense Address: St Andrew’s House, St Andrew’s Road, Chesterton, Cambridge, CB 4 1 DL, ENGLAND Voice: +44 1223 535170, FAX: +44 1223 535167, E-Mail: andy. ward@ubisense. net Re: TG 4 f Call for Preliminary Proposals and Final Proposals, IEEE P 802. 15 -09 -0419 -01 -004 f Abstract: Integration lengths for long-range PHY Purpose: To be considered by 802. 15 TG 4 f Notice: This document has been prepared to assist the IEEE P 802. 15. It is offered as a basis for discussion and is not binding on the contributing individual(s) or organization(s). The material in this document is subject to change in form and content after further study. The contributor(s) reserve(s) the right to add, amend or withdraw material contained herein. Release: The contributor acknowledges and accepts that this contribution becomes the property of IEEE and may be made publicly available by P 802. 15. Submission 1 Andy Ward, Ubisense

March, 2010 doc. : IEEE 802. 15 -10 -0192 -03 -004 f Integration lengths for long-range PHY Andy Ward Ubisense Submission 2 Andy Ward, Ubisense

March, 2010 doc. : IEEE 802. 15 -10 -0192 -03 -004 f Overview • Discuss trade-offs involved in selecting the pulse-to-symbol ratio • Show system frequency accuracy is important • Discuss ‘state-of-the-art’ in cheap crystal technology Submission 3 Andy Ward, Ubisense

March, 2010 doc. : IEEE 802. 15 -10 -0192 -03 -004 f Long-range UWB PHY • Rather than using one pulse-per-symbol mapping, we use m pulses-per-symbol • • Still very simple for transmitter to generate Still relatively simple for receivers as well! • Use a different PRF (2 MHz) so that receivers can do tone detection to figure out what type of packet is coming • Integrate the pulses at the receiver to increase signal to noise – For example, integration of four pulses increases SNR by 6 d. B (ideally) • System will be average-power limited rather than peak-power limited – Long pulse trains will mean that ‘average in 1 ms’ trick can’t be used – However, once you are average-power limited, there is no (regulatory) limit to the length of packet you can transmit at the same power Submission 4 Andy Ward, Ubisense

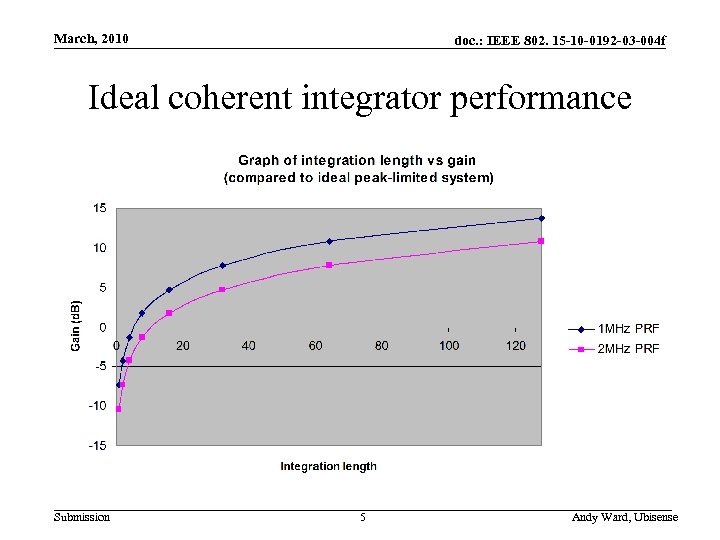March, 2010 doc. : IEEE 802. 15 -10 -0192 -03 -004 f Ideal coherent integrator performance Submission 5 Andy Ward, Ubisense

March, 2010 doc. : IEEE 802. 15 -10 -0192 -03 -004 f System frequency accuracy Nominal pulse centre time • • The previous graph assumes perfect frequency sources throughout the system When the frequency sources differ, the pulses won’t line up perfectly in the coherent receiver – So the achievable gain is less • As the number of pulses-per-symbol increases, frequency accuracy gets more important – You’re integrating over a longer time… – …so the amount of drift between the transmitter and receiver increases… – …so the pulses at the start and end of the integration period don’t line up so well Submission 6 Some time later…. Nominal pulse centre time Andy Ward, Ubisense

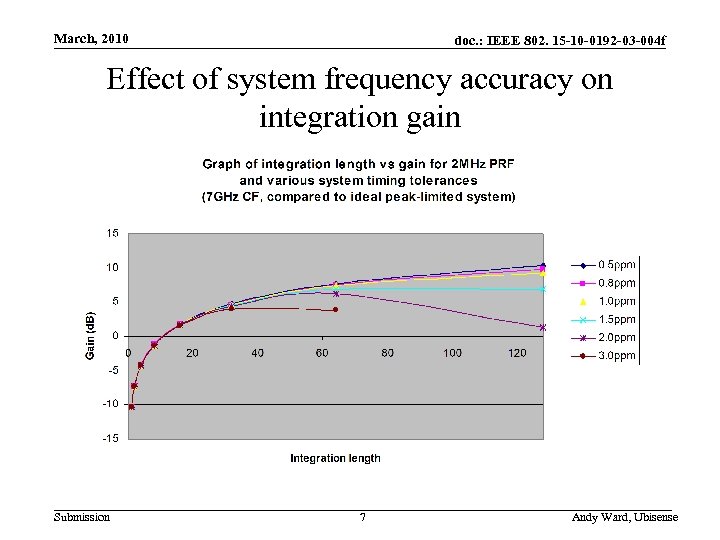March, 2010 doc. : IEEE 802. 15 -10 -0192 -03 -004 f Effect of system frequency accuracy on integration gain Submission 7 Andy Ward, Ubisense

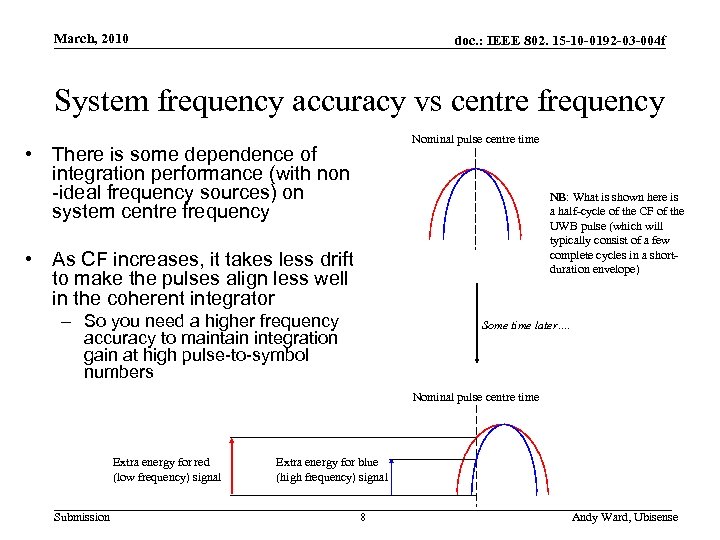March, 2010 doc. : IEEE 802. 15 -10 -0192 -03 -004 f System frequency accuracy vs centre frequency Nominal pulse centre time • There is some dependence of integration performance (with non -ideal frequency sources) on system centre frequency NB: What is shown here is a half-cycle of the CF of the UWB pulse (which will typically consist of a few complete cycles in a shortduration envelope) • As CF increases, it takes less drift to make the pulses align less well in the coherent integrator – So you need a higher frequency accuracy to maintain integration gain at high pulse-to-symbol numbers Some time later…. Nominal pulse centre time Extra energy for red (low frequency) signal Submission Extra energy for blue (high frequency) signal 8 Andy Ward, Ubisense

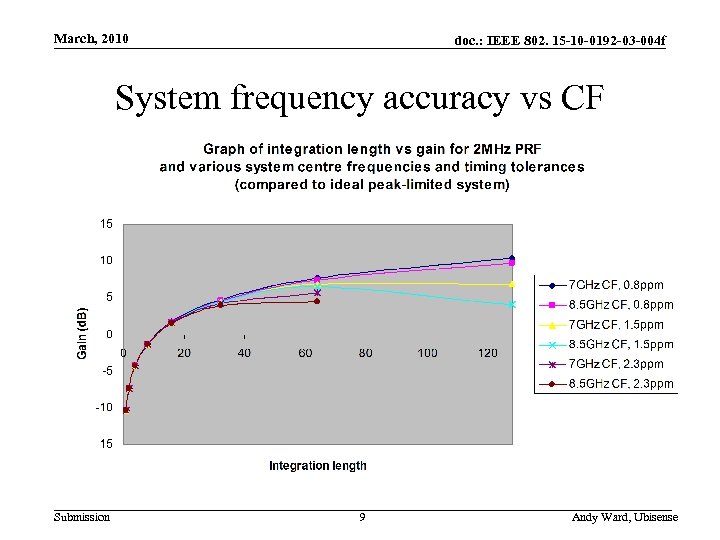March, 2010 doc. : IEEE 802. 15 -10 -0192 -03 -004 f System frequency accuracy vs CF Submission 9 Andy Ward, Ubisense

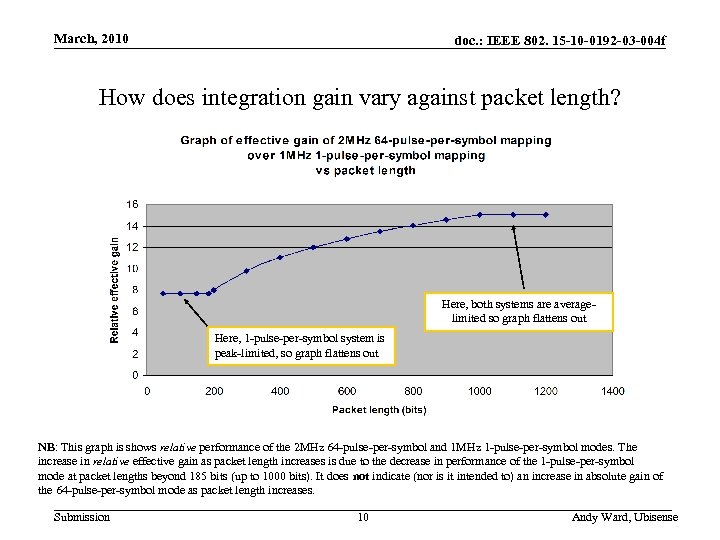March, 2010 doc. : IEEE 802. 15 -10 -0192 -03 -004 f How does integration gain vary against packet length? Here, both systems are averagelimited so graph flattens out Here, 1 -pulse-per-symbol system is peak-limited, so graph flattens out NB: This graph is shows relative performance of the 2 MHz 64 -pulse-per-symbol and 1 MHz 1 -pulse-per-symbol modes. The increase in relative effective gain as packet length increases is due to the decrease in performance of the 1 -pulse-per-symbol mode at packet lengths beyond 185 bits (up to 1000 bits). It does not indicate (nor is it intended to) an increase in absolute gain of the 64 -pulse-per-symbol mode as packet length increases. Submission 10 Andy Ward, Ubisense

March, 2010 doc. : IEEE 802. 15 -10 -0192 -03 -004 f What is a reasonable frequency tolerance to aim for? • Remember – this is ONLY relevant to systems that want to do coherent integration. You don’t need a super crystal if you don’t care about this! • • Plain crystal – maybe 10 ppm TCXO – maybe 0. 3 ppm • 0. 5 ppm TCXOs over -40 C to 85 C are now readily available – Used for GPS/GSM – Very cheap • Need to cope with other effects too: – Initial frequency accuracy (tune out at manufacture) – Crystal ageing (either tune out during use, or pre-age) • As a data point (nothing more!), system frequency accuracy budget in current Ubisense systems is better than 2 ppm – Better than 1 ppm would be achievable at same cost today Submission 11 Andy Ward, Ubisense

March, 2010 doc. : IEEE 802. 15 -10 -0192 -03 -004 f Proposal • Based on available TCXOs and integration performance, we propose a 2 MHz 64 -pulse-to-symbol mapping for the long-range UWB PHY mode, and a 2. 3 ppm system timing accuracy • This integration length and timing accuracy gives a relative gain over the 1 MHz 1 -pulse-per-symbol mapping of 4. 5 d. B at 8. 5 GHz centre frequency and packet length of 185 bits – This number increases as: • Packet length increases (up to 1000 bits) • Centre frequency decreases • Timing accuracy increases Submission 12 Andy Ward, Ubisense