Maple Обчислення границь Для обчислення границь є дві

Maple

Обчислення границь Для обчислення границь є дві команди: 1) прямого виконання – limit(expr,x=a,par), де expr – вираз, границю якого треба знайти, a – значення точки, для якої обчислюється границя, par – необов’язковий параметр для знаходження односторонніх границь (left – зліва, right – справа) або вказування типу змінної (real – дійсна, complex – комплексна). 2) відкладеного виконання – Limit(expr,x=a,par), де параметри команди такі ж, як і в попередньому випадку.

Завдання 1 Обчислити границю 2. Знайти односторонні границі і

Диференціювання Обчислення похідних. Для обчислення похідних в Maple є дві команди: 1) прямого виконання – diff(f,x), де f – функція, яку слід продиференціювати, x – змінна, по якій виконується диференціювання. 2) відкладеного виконання – Diff(f,x), де параметри команди такі ж, як і в попередній.

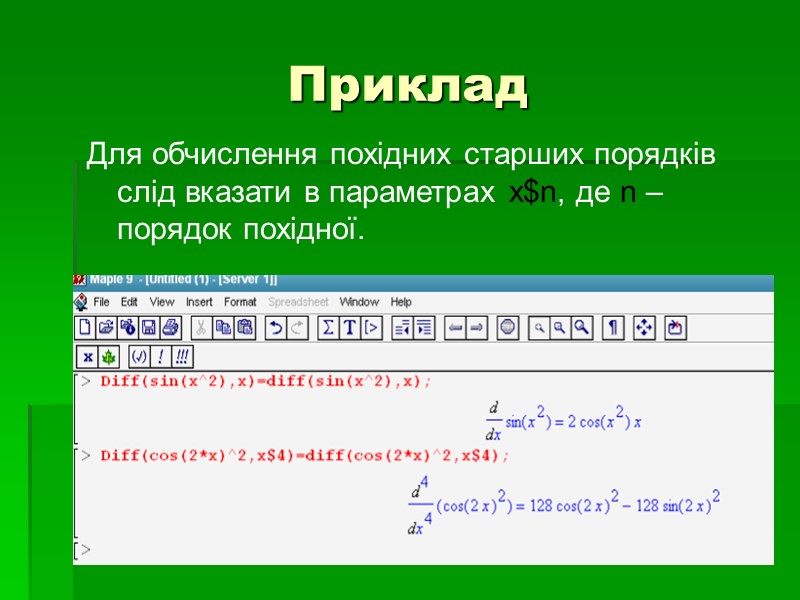
Приклад Для обчислення похідних старших порядків слід вказати в параметрах x$n, де n – порядок похідної.

Диференціальний оператор Для визначення диференціального оператора використовується команда D(f) – f-функция. Обчислення похідної в точці. Оператор диференціювання застосовується до функціональних операторів. Наприклад:

Завдання 2 Обчислити похідну Обчислити 3. Обчислити другу похідну функції в точках ,

Аналітичне и числове интегрування Невизначений інтеграл обчислюється за допомогою 2-х команд: 1) прямого виконання – int(f, x), де f – підінтегральна функція, x – змінна інтегрування; 2) відкладеного виконання – Int(f, x) – де параметри команди такі ж, як і в команді прямого виконання int. Команда Int видає на екран інтеграл в аналітичному вигляді математичної формули. Для обчислення визначеного інтеграла в командах int і Int додаються границі інтегрування. Числове інтегруваня виконується командою evalf(int(f, x=x1..x2), e), де e – точність обчислень (число знаків після коми).

Завдання 3 Знайти невизначений інтеграл 2. Знайти визначений інтеграл 3. Численно знайти інтеграл

Визначення матриці Для визначення матриці в Maple можна використовувати команду matrix(n, m, [[a11,a12,…,a1n],[a21,a22,…,a2m],…, [an1,an2,…,anm]]), де n –  число рядків, m – число стовбців в матриці. Ці числа задавати необов’язково, а достатньо перечислити елементи матриці порядково в квадратних дужках через кому. Наприклад:

Основні функції для роботи з векторами і матрицями: coldim (M) — повертає число стовбців матриці М; rowdim(M) — повертає число рядків матриці М; vectdim(V) — повертає розмірність вектора V; col(M,i) — повертає i-й стовбець матриці М; row(M,i) — повертає i-й рядок матриці М; tninor(M,i, j) — повертає мінор матриці М для елемента з індексами i и j; delcols(M,i.. j) — видаляє стовбці матриці М от i- ro до j-ro; del rows (V,i..j) — видаляє рядки матриці М от i-й до j-й; extend (М, т, n,х) — розширює матрицю М на m рядків і n стовбців використанням заповнювача х. dotprod(U,V) — скалярний добуток векторів U и V; crossprod(U,V) — векторний добуток векторів U и V; norm(V) або norm(M) — повертає норму вектора або матриці;

copyinto(A,B,i, j) — копіює матрицю А в В для елементів послідовно від i до j; concat(Ml,M2) — повертає об'єднану матрицю с горизонтальним злиттям матриць M1 и М2; stack(Ml,M2) — повертає об'єднану матрицю с вертикальним злиттям M1 и М2; matadd(A,B) та evalm(A+B) — повертає суму матриць А и В; multlply(A,B) та evalm(A&*B) — добуток матриць А и В; charpoly(M,lambda) — повертає характеристичний полином матриці М відносно заданої змінної lambda; det(M) — обчислює детермінант (визначник) матриці М; jordan(M) — повертає матрицю М в формі Жордана; hermite(M) — повертає матрицю М в ермітовій формі; trace(M) — повертає слід матриці М; rank(M) — повертає ранг матриці М; transpose(M) — повертає транспоновану матрицю М; inverse(M) або evalm(l/M) — повертає матрицю, оборотну до М; singularvals(A) — повертає сингулярні значення масиву або матриці А

Завдання 4 Дано матриці і Знайти: (АВ)С, detA, detB, detC, det[(AB)C]

Системи лінійних рівнянь і матричні рівняння Система лінійних рівнянь може бути розв’язана двома способами. Спосіб 1: стандартна команда solve знаходить розв’язок системи лінійних рівнянь, записаних в розгорнутому вигляді:

Спосіб 2: команда linsolve(A,b) із пакету linalg знаходить розв’язок рівняння . Аргументи цієї команди: А – матриця, b – вектор. За допомогою команди linsolve(A,b) можна знайти розв’язок матричного рівняння АХ=В, якщо в якості аргументів цієї команды вказати, відповідно, матриці А і В.

Завдання 5 1. Знайти загальний і один частинний розв'язок системи 2. Розв’зати матричне рівняння: АX=В; де ,

Звичайні диференціальні рівняння Для розв’язування звичайних диференціальних рівнянь і системи простих диференціальних рівнянь використовується наступна функція ядра системи: dsolve(deqn) dsolve({deqn,InC}, var ) dsolve({deqns,Inc},{vars}) dsolve({deqns,InC},{vars}, option) де deqn(s)-одне диференціальне рівняння або система із диференціальних рівнянь першого порядку, Inc початкові умови, var(s) - змінна чи змінні, відносно яких шукається розв’язок, option – необов’язковий параметр, який вказує на метод розв’язання.

Похідні при записі диференціальних рівнянь і початкових/граничних умов можуть задаватися функцією diff чи оператором D. Якщо умова на похідну задається в довільній точці х=b, то для цього задання може бути використаний оператор diff. Например, diff(y(b),b)=1. Умови на похідні в конкретной точці мають бути записані за допомогою диференціального оператора D: D(y)(0)=5, D(D(y)(4))=7.

Системи диференціальних рівнянь Команда dsolve може знайти розв’язок системи диференціальних рівнянь (або задачі Коші), якщо в ній вказать: dsolve({sys},{x(t),y(t),…}), де sys -система диференціальних рівнянь, x(t),y(t),…  -набір невідомих функцій.

Завдання 6 1. Знайти розв’язок задачі Коші: 2. Знайти розв’язок системи диференціальних рівнянь:

Джерела detc.usu.ru irodov.nm.ru soft.mail.ru