Maple Maple — програмний пакет, система комп’ютерної алгебри.

Maple

Maple — програмний пакет, система комп'ютерної алгебри. Є продуктом компанії Waterloo Maple Inc., яка з 1984 року випускає програмні продукти, орієнтовані на складні математичні обчислення, візуалізацію даних і моделювання. Система Maple призначена для символьних обчислень, хоча має ряд засобів і для чисельного вирішення диференціальних рівнянь і знаходження інтегралів. Володіє розвиненими графічними засобами. Має власну мову програмування, що нагадує Паскаль.

Версії Maple Maple 14 :29 квітня, 2010 Maple 13: 24 квітня, 2010 Maple 12: 13 травня,2010 Maple 11.02: 10 листопада, 2007 Maple 11.01: 6 липня, 2007 Maple 11: 21 лютого, 2007 Maple 10: 10 травня, 2005 Maple 9.5: 15 квітня, 2004 Maple 9: 30 червня, 2003 Maple 8: 16 квітня, 2002 Maple 7: 1 липня, 2001 Maple 6: 6 грудня, 1991 Maple V R5: 1 листопада, 1997 Maple V R4: січень 1996 Maple V R3: 15 березня, 1994 Maple V R2: листопад 1992 Maple V: серпень 1990 Maple 4.3: березень 1989 Maple 4.2: грудень 1987 Maple 4.1: травень 1987 Maple 4.0: квітень 1986 Maple 3.3: березень 1985 (Перша широко доступна версія) Maple 3.2: квітень 1984 Maple 3.1: жовтень 1983 Maple 3.0: травень 1983 Maple 2.2: грудень 1982 Maple 2.15: серпень 1982 Maple 2.1: червень 1982 Maple 2.0: травень 1982 Maple 1.1: січень 1982 Maple 1.0: січень 1982

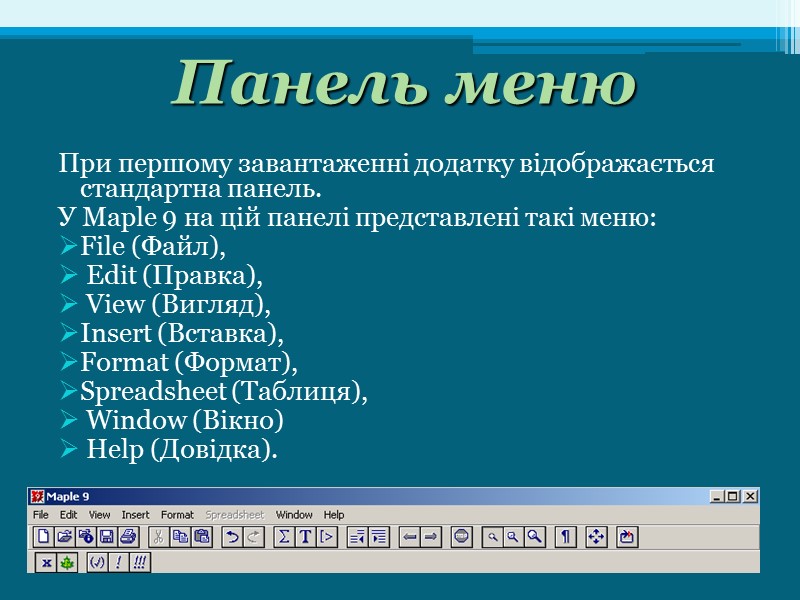
Панель меню При першому завантаженні додатку відображається стандартна панель. У Maple 9 на цій панелі представлені такі меню: File (Файл), Edit (Правка), View (Вигляд), Insert (Вставка), Format (Формат), Spreadsheet (Таблиця), Window (Вікно) Help (Довідка).

Побудова графіків Двовимірні графіки. Для побудови графіків використовують команду plot. Для побудови графіків функції f(x) однієї змінної (у інтервалі а ≤x ≤b по осі Ох і в інтервалі c ≤ y≤d по осі Оу) використовується команда plot(f(x), x=a..b, y=c..d, parameters), де parameters – параметри управління зображенням. Розглянемо деякі приклади.

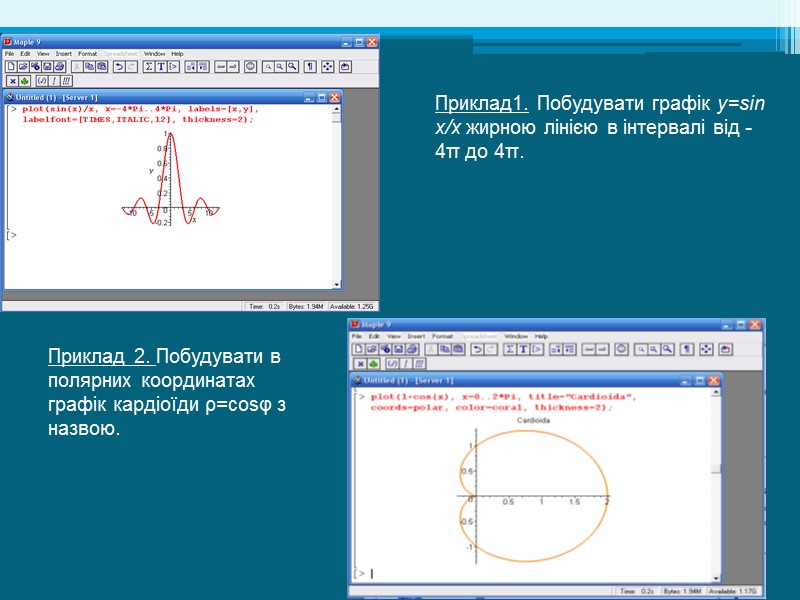
Приклад 2. Побудувати в полярних координатах графік кардіоїди ρ=cosφ з назвою. Приклад1. Побудувати графік y=sin x/x жирною лінією в інтервалі від -4π до 4π.

Побудова графіка функції, заданої неявно. Команда implicitplot: implicitplot(F(x,y)=0, x=x1..x2, y=y1..y2). Виведення текстових коментарів на малюнок. Команда textplot: textplot([xo,yo,’text’], options), де xo, уо – координати точки, з якою починається виведення тексту ’text’. Виведення декількох графічних об'єктів на один малюнок. Для цього результат дії команди привласнюється деякій змінній: > p:=plot(.): t:=textplot(.): Для виведення графічних зображень необхідно виконати команду із пакету plots: > with(plots): display([p,t], options).

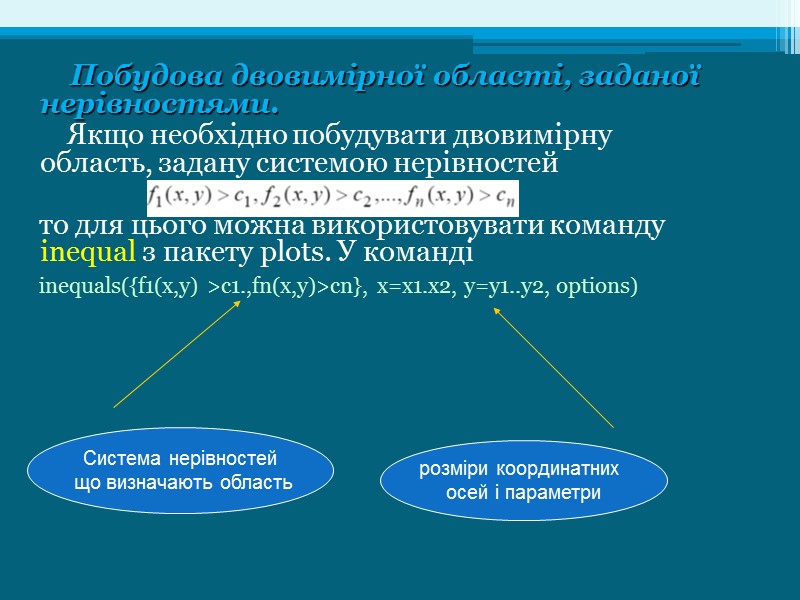
Побудова двовимірної області, заданої нерівностями. Якщо необхідно побудувати двовимірну область, задану системою нерівностей то для цього можна використовувати команду inequal з пакету plots. У команді inequals({f1(x,y) >c1.,fn(x,y)>cn}, x=x1.x2, y=y1..y2, options) Система нерівностей що визначають область розміри координатних осей і параметри

– optionsfeasible=(color=red) – установка кольору внутрішньої області; – optionsexcluded=(color=yellow) – установка кольору зовнішньої області; – optionsopen(color=blue, thickness=2) – установка кольору і товщини лінії відкритого кордону; – optionsclosed(color=green,thickness=3) – установка кольору і товщини лінії закритого кордону.

Побудуємо на одному малюнку графіки астроїди , вписаною в еліпс і виведемо назву ліній Astroida і Ellips жирним шрифтом разом з його рівнянням курсивом. Для цього наберемо наступні рядки: > with(plots): > eq:=x^2/16+y^2/4=1: > el:=implicitplot(eq, x=-4..4, y=-2..2, scaling=CONSTRAINED, color=green, thickness=3): > as:=plot([4*cos(t)^3,2*sin(t)^3, t=0..2*Pi],

color=blue, scaling=CONSTRAINED, thickness=2): > eq1:=convert(eq,string): > t1:=textplot([1.5,2.5,eq1], font=[TIMES, ITALIC, 10], align=RIGHT): > t2:=textplot([0.2,2.5,"Ellips:"], font=[TIMES, BOLD,10], align=RIGHT): > t3:=textplot([1.8,0.4,Astroida], font=[TIMES, BOLD,10], align=LEFT): display([as,el,t1,t2,t3]);

2) Тривимірні графіки та анімації Графік функції z =f (x, y) можна намалювати, використовуючи команду plot3d(f(x,y), x=x1.x2, y=y1.y2, options). До часто використовуваних параметрів команди plot3d відноситься : light=[angl1, angl2, c1, c2, c3] – завдання підсвічування поверхні, що створюється джерелом світла з точки з сферичними координатами (angl1, angl2); style=opt - задає стиль малюнка; shading=opt задає функцію інтенсивності заповнювача, його значення рівне xyz – за замовчуванням.

Графік поверхні, заданої параметрично. Щоб побудувати поверхню: x=x(u,v), y=y(u,v), z=z(u,v), то ці функції перераховуються в квадратних дужках в команді: plot3d([x(u,v), у(u,v), z(u,v)], u=u1..u2, v=v1..v2). Графік поверхні, що задана неявно. Тривимірний графік поверхні F(x, y, z) = c , будується за допомогою команди пакету plot: implicitplot3d(F(x,y,z)=c, x=x1..x2, y=y1..y2, z=z1..z2). Графік просторових кривих. Команда spacecurve для побудови просторової кривої: x = x(t), у=у(t), z = z(t). Параметри команди: spacecurve([x(t),y(t),z(t)],t=t1..t2), де змінна t змінюється від t1 до t2 .

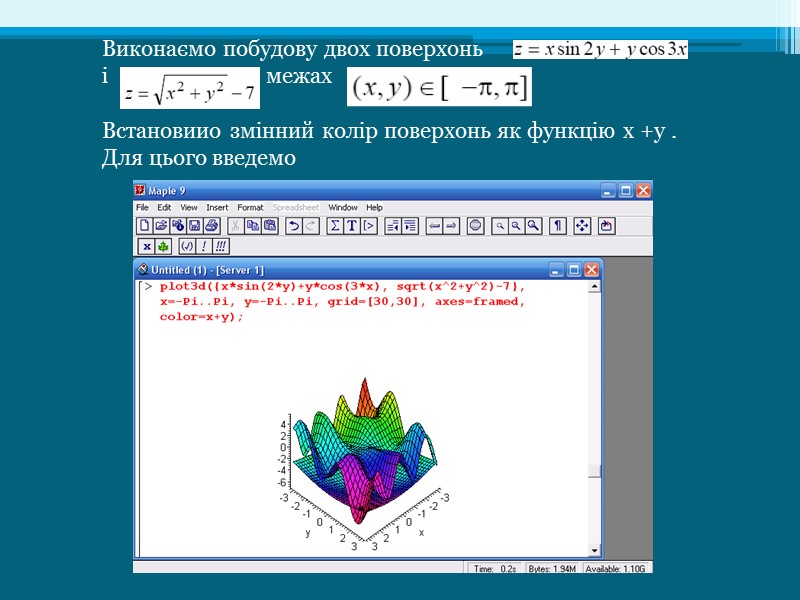
Виконаємо побудову двох поверхонь і в межах Встановиио змінний колір поверхонь як функцію x +у . Для цього введемо

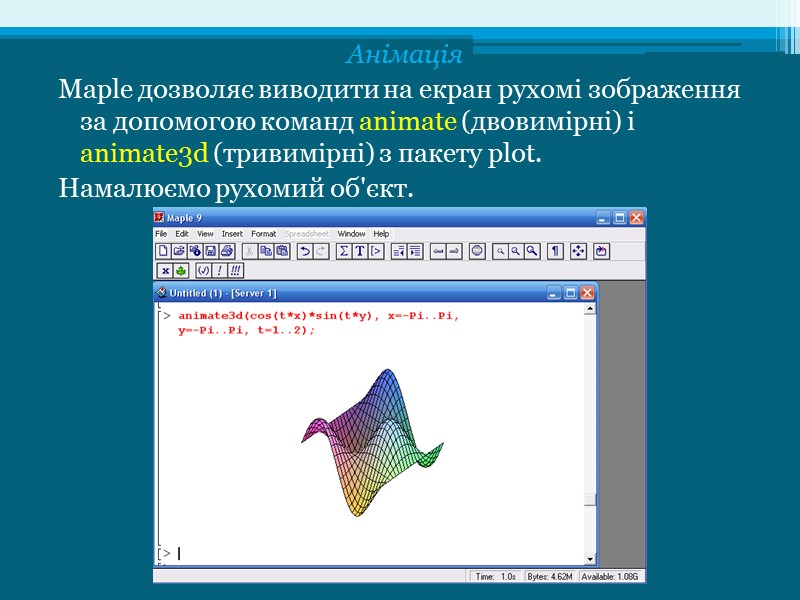
Анімація Maple дозволяє виводити на екран рухомі зображення за допомогою команд animate (двовимірні) і animate3d (тривимірні) з пакету plot. Намалюємо рухомий об'єкт.

Для того, щоб анімація виконувалася клацнемо по зображенню правою кнопкою миші і у контекстному меню, що з'явилося, виконаємо наступну команду Animation/ Continuous. Потім знову викликаємо контекстне меню і виконуємо командуAnimation/Play

Для того, щоб зупинити рух, виконаємо команду Animation/Stop. Потім за допомогою миші можна повернути рисунок під іншим кутом і зробити його знову рухомим.

Список використаних джерел: 1) Дьяконов В.П. Математическая система Maple V R3/R4/R5. М.:Солон, 1998. 2) Методы решения математических задач в Maple. http://www.foxitsoftware.com For evaluation only 3) http://maple9.info.