Making Simple Decisions Utility Theory Multi

Making Simple Decisions • Utility Theory • Multi. Attribute Utility Functions • Decision Networks • The Value of Information • Summary

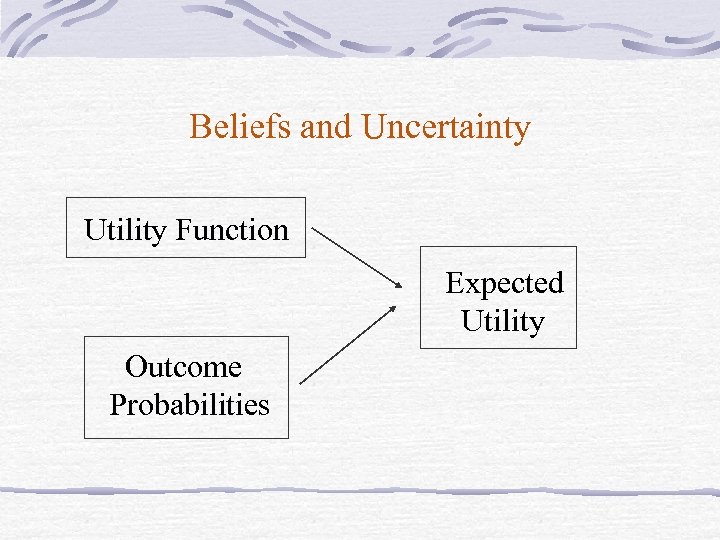Beliefs and Uncertainty Utility Function Expected Utility Outcome Probabilities

Maximum Expected Utility EU(A|E) = Σ P(Resulti(A) | E) U(Resulti(A)) Principle of Maximum Expected Utility: Choose action A with highest EU(A|E)

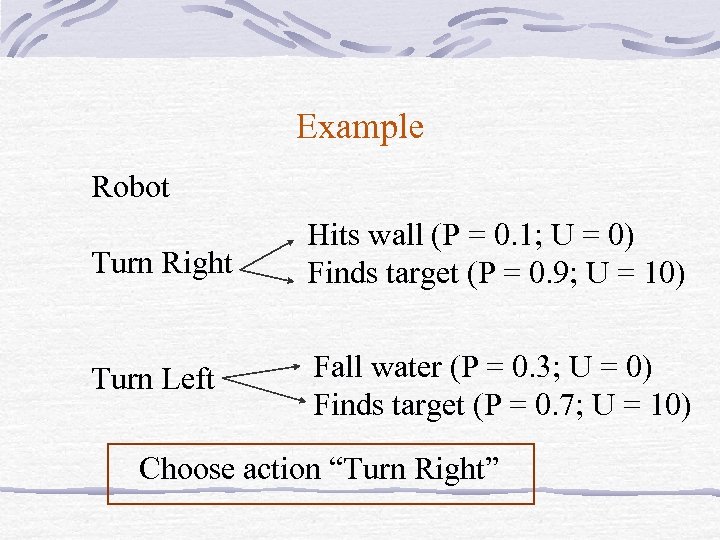Example Robot Turn Right Hits wall (P = 0. 1; U = 0) Finds target (P = 0. 9; U = 10) Turn Left Fall water (P = 0. 3; U = 0) Finds target (P = 0. 7; U = 10) Choose action “Turn Right”

Notation Utility Theory A > B A is preferred to B A ~ B indifferent between A and B A >~ B A is preferred to or indifferent to B Lottery (or random variable) L = [p 1, S 1; p 2, S 2; …, pn, Sn] where p: probability and S: outcome

Utility Principle U(A) > U(B) A > B U(A) = U(B) A ~ B

Utility Functions Television Game Show: Assume you already have won $1, 000 Flip a coin: Tails (P = 0. 5) Head (P = 0. 5) $3, 000 $0

Utility Functions EU(Accept) = 0. 5 U(Sk) + 0. 5 U(Sk + 3 M) EU(Decline) = U(Sk + 1 M) Assume: Sk = 5 Sk + 1 M = 8 Sk + 3 M = 10

Utility Functions Then EU(Accept) = 0. 5 x 5 + 0. 5 x 10 = 7. 5 EU(Decline) = 8 Result: Decline offer in view of assigned utilities

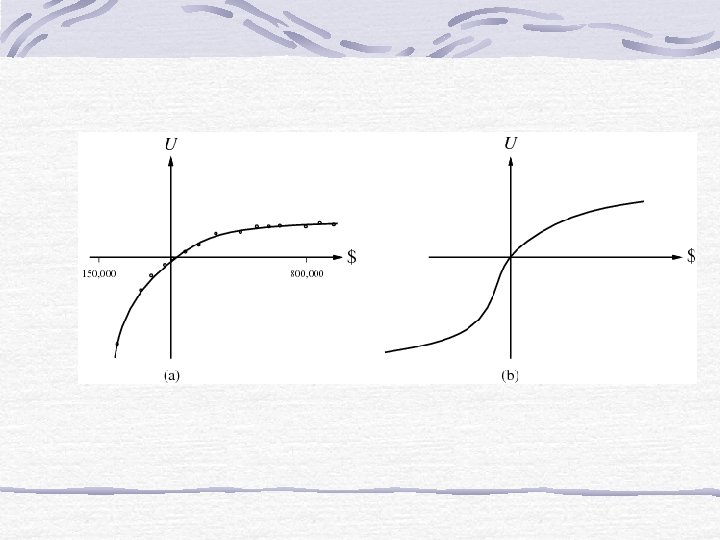
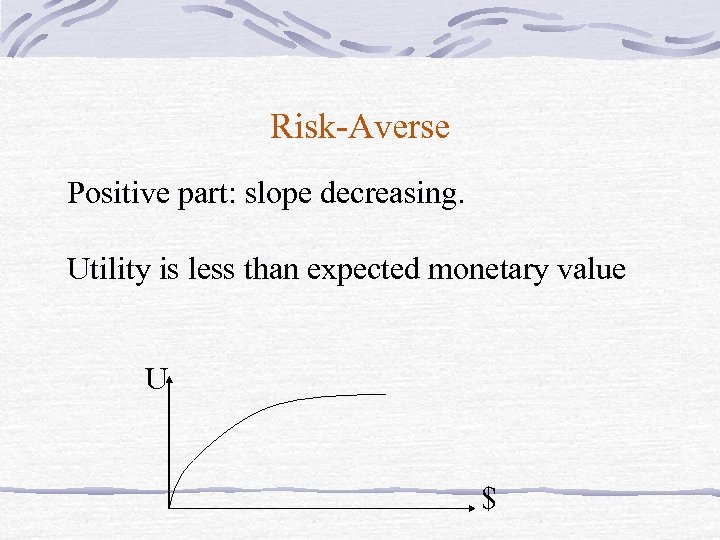Risk-Averse Positive part: slope decreasing. Utility is less than expected monetary value U $

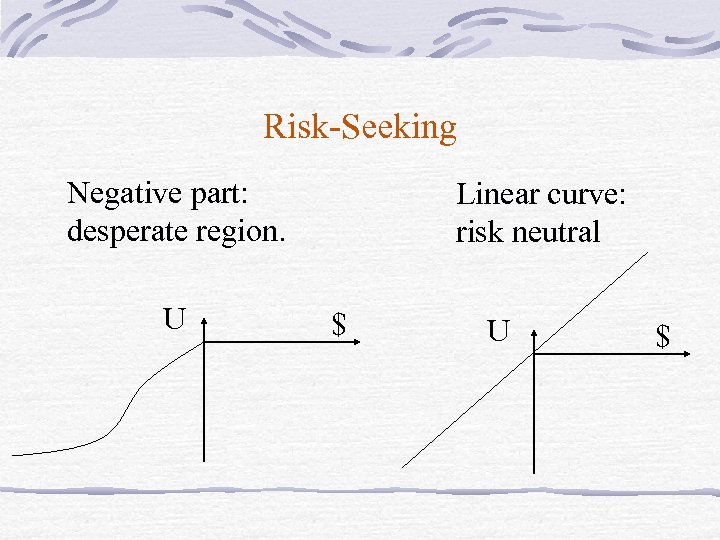Risk-Seeking Negative part: desperate region. U Linear curve: risk neutral $ U $

Connection to AI • Choices are as good as the preferences they are based on. • If user embeds in our intelligent agents : • contradictory preferences Results may be negative • reasonable preferences Results may be positive

Assessing Utilities Best possible outcome: Amax Worst possible outcome: Amin Use normalized utilities: U(Amax) = 1 ; U(Amin ) = 0

Making Simple Decisions • Utility Theory • Multi. Attribute Utility Functions • Decision Networks • The Value of Information • Summary

Multi. Attribute Utility Functions Outcomes are characterized by more than one attribute: X 1, X 2, …, Xn Example: Choosing right map Finding right equipment Acquiring food supplied successful trip unsuccessful trip

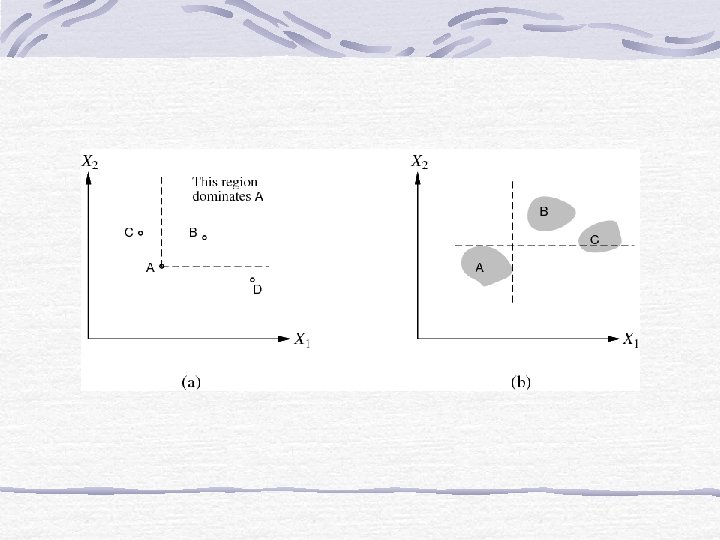
Simple Case: Dominance Assume higher values of attributes correspond to higher utilities. There are regions of clear “dominance”

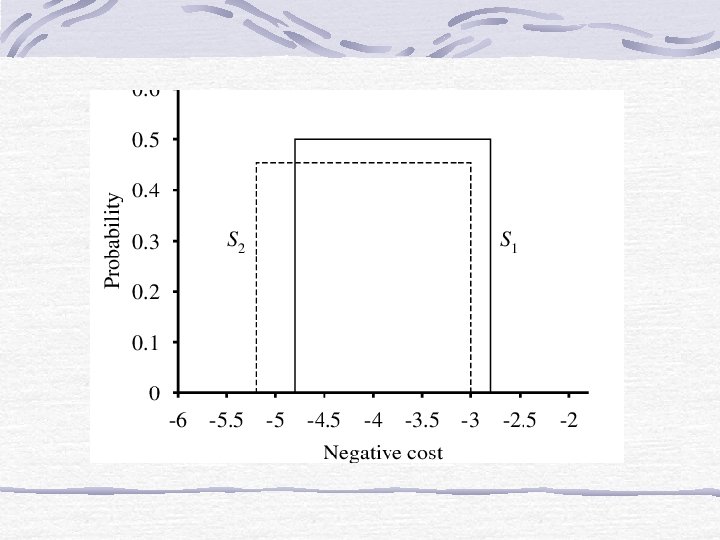
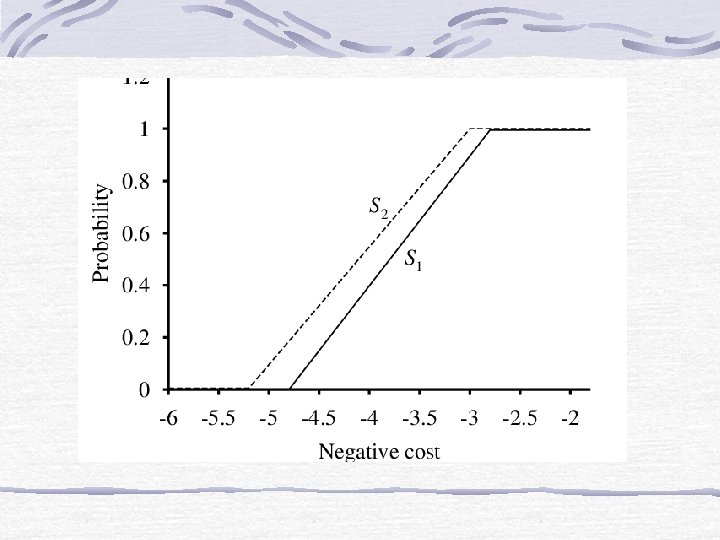
Stochastic Dominance Plot probability distributions against negative costs. Example: S 1: Build airport at site S 1 S 2: Build airport at site S 2

Making Simple Decisions • Utility Theory • Multi. Attribute Utility Functions • Decision Networks • The Value of Information • Summary

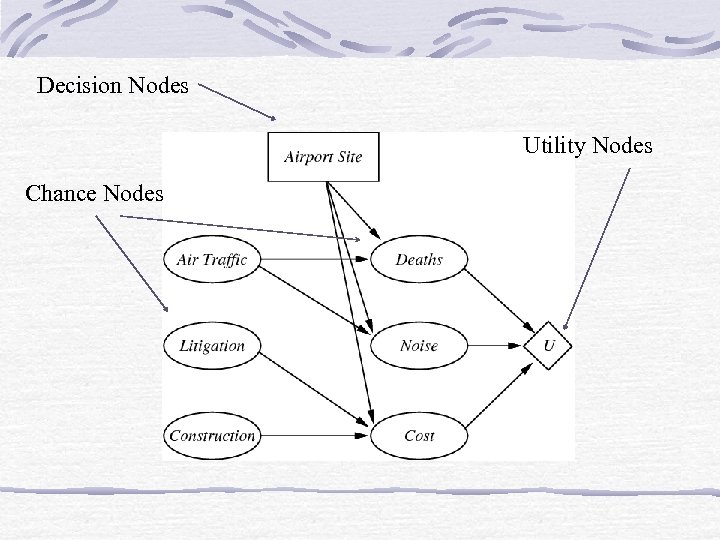
Decision Networks • It’s a mechanism to make rational decisions • Also called influence diagram • Combine Bayesian Networks with other nodes

Types of Nodes • Chance Nodes. Represent random variables (like BBN) • Decision Nodes Choice of action • Utility Nodes Represent agent’s utility function

Decision Nodes Utility Nodes Chance Nodes

Making Simple Decisions • Utility Theory • Multi. Attribute Utility Functions • Decision Networks • The Value of Information • Summary

The Value of Information Important aspect of decision making: What questions to ask. Example: Oil company. Wishes to buy n blocks of ocean drilling rights.

The Value of Information Exactly one block has oil worth C dollars. The price of each block is C/n. A seismologist offers the results of a survey of block number 3. How much would you pay for the info?

The Value of Information • With probability 1/n the survey will indicate there is oil in block 3. Buy it for C/n dollars to make a profit of C – C/n = (n-1) C / n • With probability (n-1)/n the survey will show no oil. Buy different block. Expected profit is C/(n-1) – C/n = C/n(n-1) dollars.

Expected Profit The expected profit given the info is 1/n x (n-1)C / n + (n-1)/n x C / n(n-1) = C/n The info. is worth the price of the block itself.

The Value of Information Value of info: Expected improvement in utility compared with making a decision without that information.

Making Simple Decisions • Utility Theory • Multi. Attribute Utility Functions • Decision Networks • The Value of Information • Summary

Summary • Decision theory combines probability and utility theory. • A rational agent chooses the action with maximum expected utility. • Multiattribute utility theory deals with utilities that depend on several attributes • Decision networks extend BBN with additional nodes • To solve a problem we need to know the value of information.

Video Rover Curiosity explores Mars (decision making is crucial during navigation) https: //www. youtube. com/watch? v=W 6 Bdi. KIWJh. Y