Making Simple Decisions Chapter 16 Der Rong Din

Making Simple Decisions Chapter 16 Der Rong Din CSIE/NCUE/2005 Copyright, 1996 © Dale Carnegie & Associates, Inc.

Outline Combining beliefs and desires under Uncertainty The basis of Utility Theory Utility functions Multiattribute Utility functions Decision Networks The value of Information Decision Theoretic Expert Systems Der Rong Din CSIE/NCUE/2005 2

Combining beliefs and desires Decision theoretic agent n n n An agent that can make rational decisions based on what it believes and what it wants. Can make decisions in contexts where uncertainty and conflicting goals. Has a continuous measure of state quality. Goal based agent n Has a binary distinction between good(goal) and bad(non goal) states. We can make decision based on probabilistic reasoning (Belief Networks), but it does not include what an gent wants. An agent’s preferences between world states are captured by a utility function it assigns a single number to express the desirability of a state. Utilities are combined with the outcome probabilities for actions to give an expected utility for each action. Der Rong Din CSIE/NCUE/2005 3

The utility function U(S) • An agent’s preferences between different states S in the world are captured by the Utility function U(S). If U(Si) > U(Sj) then the agent prefers state Si before state Sj If U(Si) = U(Sj) then the agent is indifferent between the two states Si and Sj Der Rong Din CSIE/NCUE/2005 4

Combining Belief and Desires Utility: captures the desirability of a state, U(S) A: nondeterministic action Resulti(A): Outcome states of action A E: available evidences of the world Do(A): perform action A EU: expected utility EU(A|E) = ∑ i. P(Resulti(A) | Do(A), E) * U(Resulti(A)) Der Rong Din CSIE/NCUE/2005 5

MEU MEU: maximum expected utility A rational agent should choose an action that maximizes the agent’s expected utility Simple decision: (single action) Complex decision: sequences decisions This is a framework where all of the components of an AI system fit If an agent maximizes a utility function that correctly reflects the performance measure by which its behavior is being judged, then it will achieve the highest possible performance score if we average over the environments in which the agent could be placed. Der Rong Din CSIE/NCUE/2005 6

16. 2 The basis of utility theory Why should maximizing the average utility be so special? Constraints on rational preferences are orderability, transitivity, continuity, substitutability, monotonicity, decomposability. The six constraints form the axioms of utility theory. The axioms of utility: n n Utility principle Maximum Expected Utility principle Der Rong Din CSIE/NCUE/2005 7

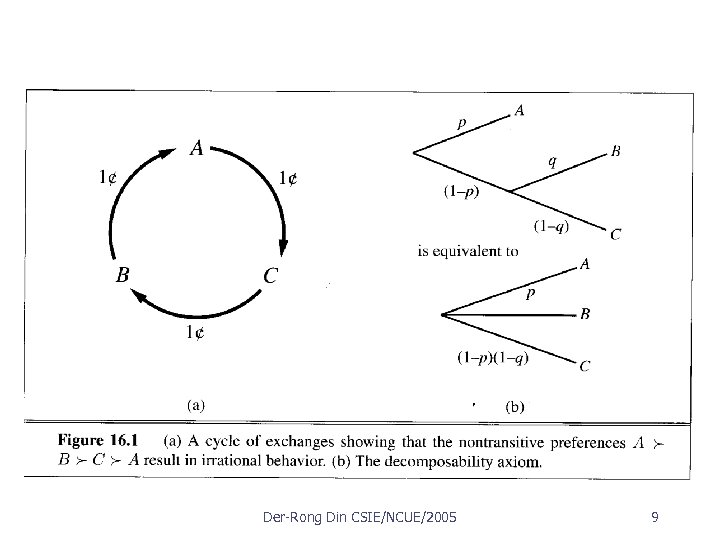
Constraints on rational preference Der Rong Din CSIE/NCUE/2005 8

Der Rong Din CSIE/NCUE/2005 9

The six axioms of utility theory Der Rong Din CSIE/NCUE/2005 10

Utility principle If an agent’s preferences obey the axioms of utility, then there exists a real valued function U that operates on states such that U(A) > U(B) if and only if A is preferred to B and U(A) = U(B) if and only if the agent is indifferent to A and B. n n U(A) > U(B) A > B U(A) = U(B) A ~ B Maximum Expected Utility principle n n The utility of a lottery is the sum of the probability of each outcome times the utility of that outcome. U([p 1, S 1; … ; pn, Sn]) = ∑ pi U(Si) Der Rong Din CSIE/NCUE/2005 11

16. 3 Utility functions map states to real numbers. Agent can have any preference it likes. Preferences can also interact. Utility theory has its roots in economics > the utility of money Der Rong Din CSIE/NCUE/2005 12

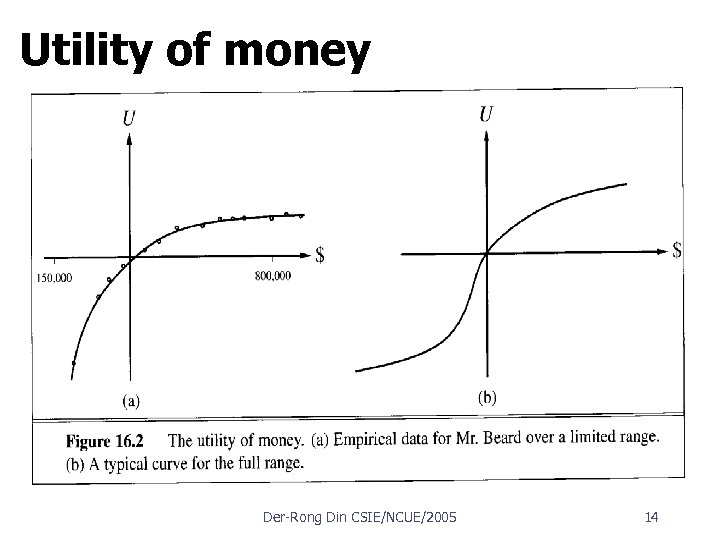
Utility of money, Figure 16. 2 Monotonic preference for definite amounts of money. Expected Monetary Value, EMV n n Sn : the state of processing wealth $n take $1000 or 50% chance of $3000 EU(Accept) =. 5 *U(Sk) +. 5*U(Sk+3000) EU(Decline) = U(Sk+1000) Der Rong Din CSIE/NCUE/2005 13

Utility of money Der Rong Din CSIE/NCUE/2005 14

Utility of money n n Risk averse Risk seeking Certainty equivalent Risk neutral Utility scales and utility assessment n Utility functions are not unique w U’(S) = k 1 + k 2 * U(S), k 2 > 0 n n Normalization Standard lottery w u┬, best possible outcome, 1 w u┴, worst possible outcome, 0 Micromort (1: 1, 000 chance of death), $20 in 1980 QALY: quality adjusted life year Der Rong Din CSIE/NCUE/2005 15

6. 4 MULTIATTRIBUTE UTILITY FUNCTIONS Problem’s outcomes are characterized by two or more attributes, are handled by multiattribute utility theory. The attributes X = X 1, . . . , Xn; a complete vector of assignments will be x = (x 1, . . . , xn). Each attribute is generally assumed to have discrete or continuous scalar values. Der Rong Din CSIE/NCUE/2005 16

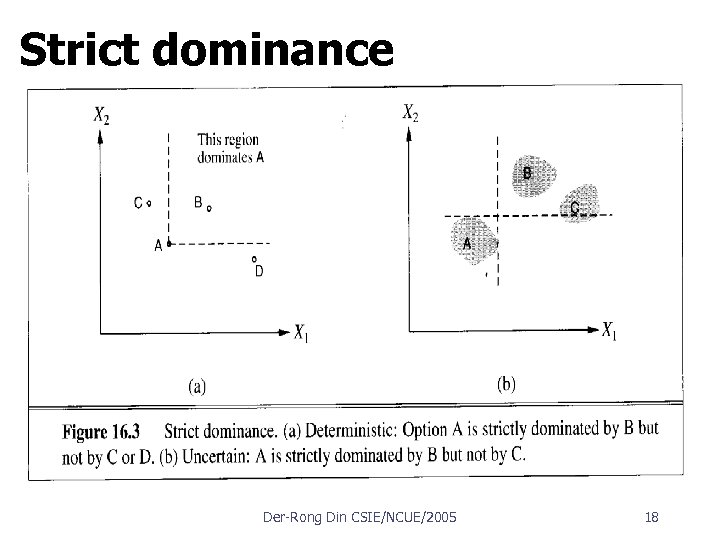
Dominance Suppose that airport site S 1 costs less, generates less noise pollution, and is safer than site S 2. One would not hesitate to reject S 2. We then say that there is strict dominance of S 1 over S 2. In general, if an option is of lower value on all attributes than some other option, it need not be considered further. Strict dominance is often very useful in narrowing down the field of choices to the real contenders, although it seldom yields a unique choice. Der Rong Din CSIE/NCUE/2005 17

Strict dominance Der Rong Din CSIE/NCUE/2005 18

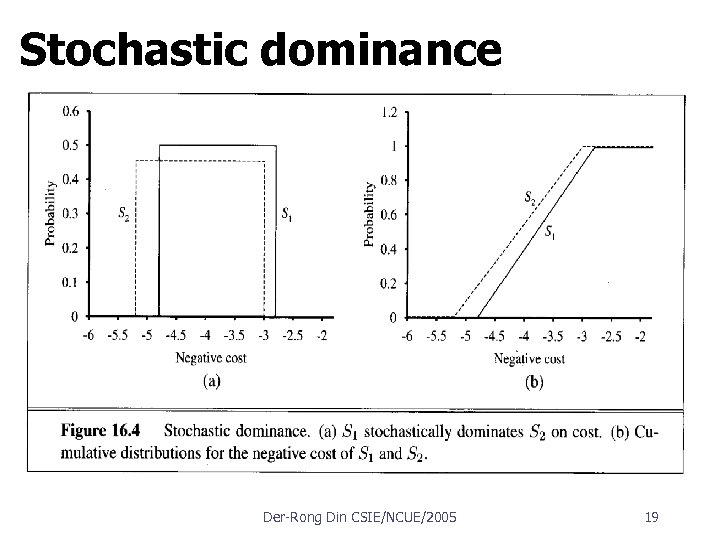Stochastic dominance Der Rong Din CSIE/NCUE/2005 19

CDF Der Rong Din CSIE/NCUE/2005 20

Der Rong Din CSIE/NCUE/2005 21

Preference without uncertainty Der Rong Din CSIE/NCUE/2005 22

Preference with uncertainty Der Rong Din CSIE/NCUE/2005 23

6. 5 Decision networks Extend Bayesian nets to handle actions and utilities n a. k. a. influence diagrams Make use of Bayesian net inference Useful application: Value of Information Der Rong Din CSIE/NCUE/2005 24

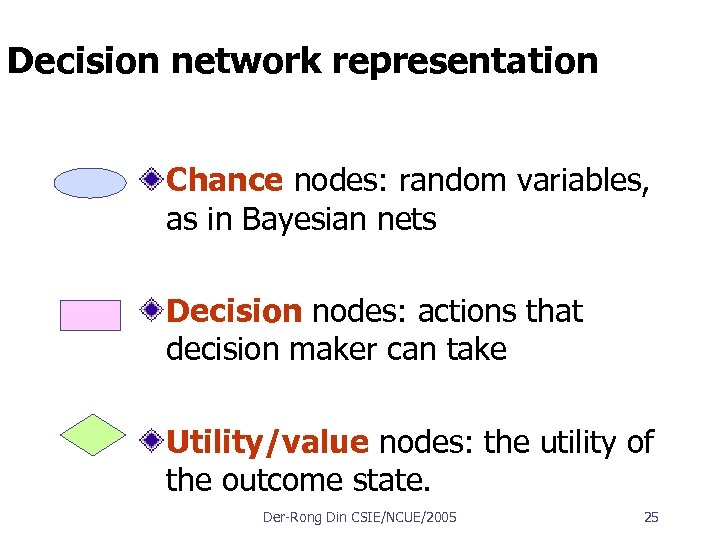Decision network representation Chance nodes: random variables, as in Bayesian nets Decision nodes: actions that decision maker can take Utility/value nodes: the utility of the outcome state. Der Rong Din CSIE/NCUE/2005 25

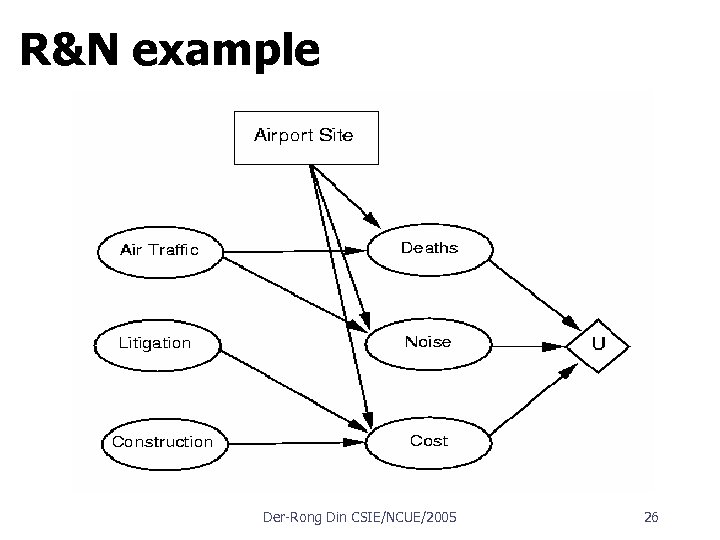R&N example Der Rong Din CSIE/NCUE/2005 26

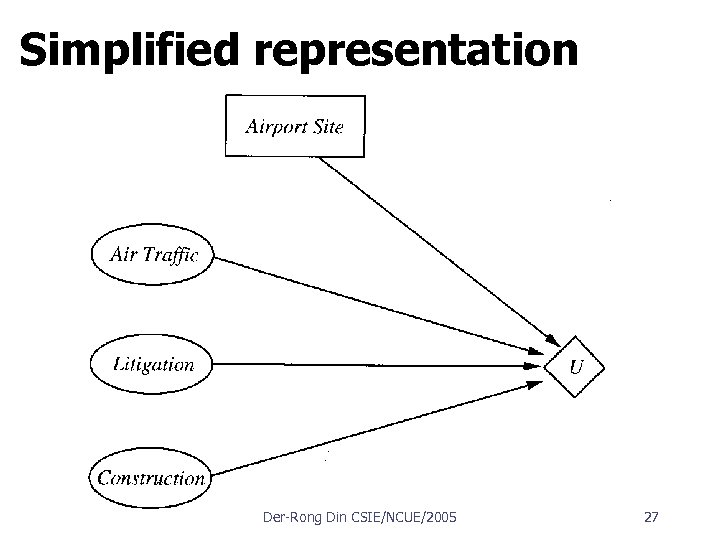Simplified representation Der Rong Din CSIE/NCUE/2005 27

Evaluating decision networks Set the evidence variables for the current state. For each possible value of the decision node (assume just one): n Set the decision node to that value. n Calculate the posterior probabilities for the parent nodes of the utility node, using BN inference. n Calculate the resulting utility for the action. Return the action with the highest utility. Der Rong Din CSIE/NCUE/2005 28

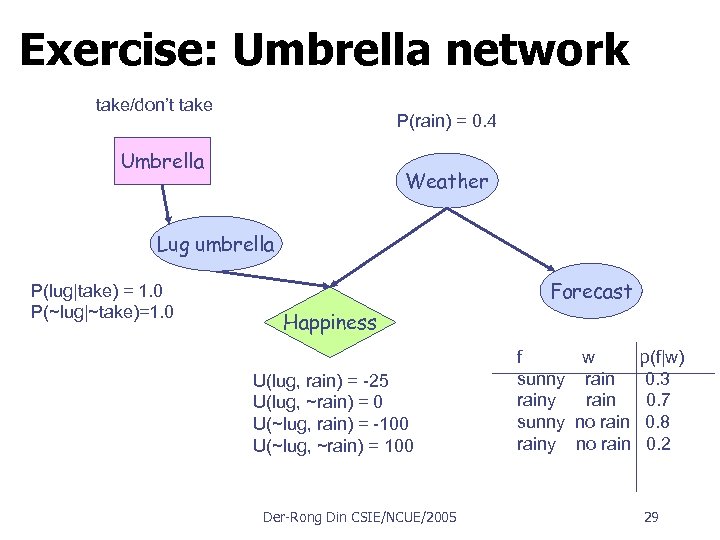Exercise: Umbrella network take/don’t take P(rain) = 0. 4 Umbrella Weather Lug umbrella P(lug|take) = 1. 0 P(~lug|~take)=1. 0 Forecast Happiness U(lug, rain) = -25 U(lug, ~rain) = 0 U(~lug, rain) = -100 U(~lug, ~rain) = 100 Der Rong Din CSIE/NCUE/2005 f w p(f|w) sunny rain 0. 3 rainy rain 0. 7 sunny no rain 0. 8 rainy no rain 0. 2 29

16. 6 The value of information One of the most important parts of decision making is knowing what questions to ask. For example, a doctor cannot expect to be provided with the results of all possible diagnostic tests and questions at the time a patient first enters the consulting room. Tests are often expensive and sometimes hazardous (both directly and because of associated delays). Their importance depends on two factors: n n whether the test results would lead to a significantly better treatment plan, and how likely the various test results are. Der Rong Din CSIE/NCUE/2005 30

Information value theory information value theory, which enables an agent to choose what information to acquire. The acquisition of information is achieved by sensing actions. Because the agent's utility function seldom refers to the contents of the agent's internal state, whereas the whole purpose of sensing actions is to affect the internal state, we must evaluate sensing actions by their effect on the agent's subsequent "real" actions. Thus, information value theory involves a form of sequential decision making. Der Rong Din CSIE/NCUE/2005 31

Simple example Suppose an oil company is hoping to buy one of n indistinguishable blocks of ocean drilling rights. Let us assume further that exactly one of the blocks contains oil worth C dollars and that the price of each block is C/n dollars. If the company is risk neutral, then it will be indifferent between buying a block and not buying one. Now suppose that a seismologist offers the company the results of a survey of block number 3, which indicates definitively whether the block contains oil. How much should the company be willing to pay for the information? With probability 1/n, the survey will indicate oil in block 3. In this case, the company will buy block 3 for C/n dollars and make a profit of n C - C/n = (n - 1)C/n dollars. With probability (n-1)/n, the survey will show that the block contains no oil, in which case the company will buy a different block. Now the probability of finding oil in one of the other blocks changes from 1/n to 1/(n — 1), so the company makes an expected profit of n C/(n - 1) C/n = C/n(n - 1) dollars. Der Rong Din CSIE/NCUE/2005 32

Simple example The value of information derives from the fact that with the information, one's course of action can be changed to suit the actual situation. One can discriminate according to the situation, whereas without the information, one has to do what's best on average over the possible situations. In general, the value of a given piece of information is defined to be the difference in expected value between best actions before and after information is obtained. Der Rong Din CSIE/NCUE/2005 33

Value of Perfect Information (VPI) How much is it worth to observe (with certainty) a random variable X? Suppose the agent’s current knowledge is E. The value of the current best action is: EU(α | E) = max. A ∑i U(Resulti(A)) p(Resulti(A) | E, Do(A)) The value of the new best action after observing the value of X is: EU(α’ | E, X) = max. A ∑i U(Resulti(A)) p(Resulti(A) | E, X, Do(A)) …But we don’t know the value of X yet, so we have to sum over its possible values The value of perfect information for X is therefore: VPI(X) = ( ∑k p(xk | E) EU(αxk | xk, E)) – EU (α | E) Probability of each value of X Expected utility of the best action given that value of X Der Rong Din CSIE/NCUE/2005 Expected utility of the best action if we don’t know X 34 (i. e. , currently)

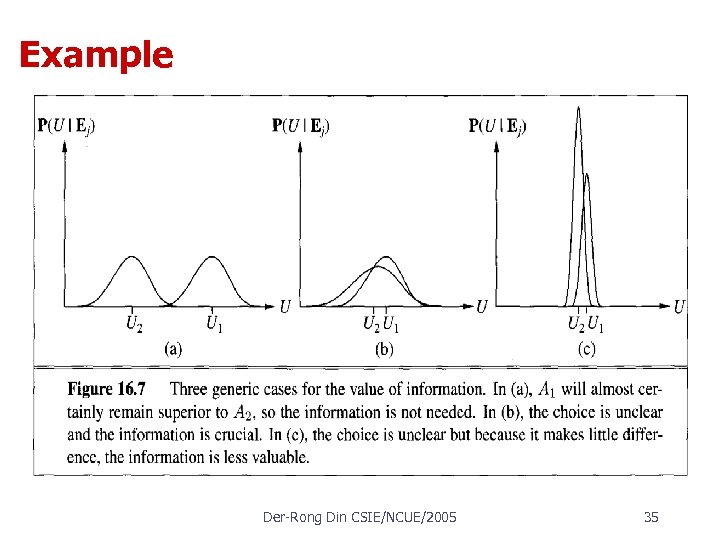Example Der Rong Din CSIE/NCUE/2005 35

VPI exercise: Umbrella network What’s the value of knowing the weather forecast before leaving home? take/don’t take P(rain) = 0. 4 Umbrella Weather Lug umbrella P(lug|take) = 1. 0 P(~lug|~take)=1. 0 Happiness U(lug, rain) = -25 U(lug, ~rain) = 0 U(~lug, rain) = -100 U(~lug, ~rain) = 100 Der Rong Din CSIE/NCUE/2005 Forecast f w p(f|w) sunny rain 0. 3 rainy rain 0. 7 sunny no rain 0. 8 rainy no rain 0. 2 36

The value of information One of the most important parts of decision making is knowing what questions to ask. To conduct expensive and critical tests or not depends on two factors: n n Whether the different possible outcomes would make a significant difference to the optimal course of action The likelihood of the various outcomes Information value theory enables an agent to choose what information to acquire. Der Rong Din CSIE/NCUE/2005 37

Properties of the value of information Der Rong Din CSIE/NCUE/2005 38

Information-gathering agent Der Rong Din CSIE/NCUE/2005 39

16. 7 Decision-theoretic expert systems The decision maker states preferences between outcomes. The decision analyst enumerates the possible actions and outcomes and elicits preferences from the decision maker to determine the best course of action. The addition of decision networks means that expert systems can be developed that n n recommend optimal decisions, reflecting the preferences of the user as well as the available evidence. Der Rong Din CSIE/NCUE/2005 40

Design process Create a causal model. n Determine what are the possible symptoms, disorders, treat ments, and outcomes. Simplify to a qualitative decision model. Assign probabilities. n Probabilities can come from patient databases, literature studies, or the expert's subjective assessments. Assign utilities. n When there a small number of possible outcomes, they can be enumerated and evaluated individually. Verify and refine the model. n To evaluate the system we will need a set of correct (input, output) pairs; a so called gold standard to compare against. Der Rong Din CSIE/NCUE/2005 41

Design process Perform sensitivity analysis. n n n This important step checks whether the best decision is sensitive to small changes in the assigned probabilities and utilities by systematically varying those parameters and running the evaluation again. If small changes lead to significantly different decisions, then it could be worthwhile to spend more resources to collect better data. If all variations lead to the same decision, then the user will have more confidence that it is the right decision. Sensitivity analysis is particularly important, because one of the main criticisms of probabilistic approaches to expert systems is that it is too difficult to assess the Der Rong Din CSIE/NCUE/2005 42

Inference diagram Der Rong Din CSIE/NCUE/2005 43

Summary Probability theory describes what an agent should believe based on evidence Utility theory describes what an agent wants Decision theory puts the two together to describe what an agent should do A rational agent should select actions that maximize its expected utility. Decision networks provide a simple formalism for expressing and solving decision problems. Der Rong Din CSIE/NCUE/2005 44