Maintaining Stream Statistics Over Sliding Windows Paper by

Maintaining Stream Statistics Over Sliding Windows Paper by Mayur Datar, Aristides Gionis, Piotr Indyk, Rajeev Motwani Presentation by Adam Morrison.

Sliding Window Intro l. Infinite stream. l. Only last N elements relevant. – Packet streams. l N is huge. – Stronger model…

Model l. Count memory bits. l. Online algorithm. Arrival: Timestamp: 1 2 3 4 5 6 7 3 2 1 3 1 1 2

Plan l. Basic Counting – Given a bit stream, maintain at every time instant the count of 1 s in the last N elements. l. Sum – Given an integer stream, maintain the sum of the last N elements. l. Everything else

Basic Counting l. Exact Solution? 2 (Counter? ) Exact solution requires (N) bits. 1 2 1 1 0

Approximate Basic Counting l. Solution: Approximate the answer and bound the relative error =0. 05 95 100 105

Bucket sizes? The idea Policy for creating new l. Dynamic histogrambuckets? 1 s. of active l. New 1 s go into right most bucket. What is it good for? l. For each bucket keep the timestamp of the most recent 1 and the bucket’s size. l. When timestamp expires, free bucket.

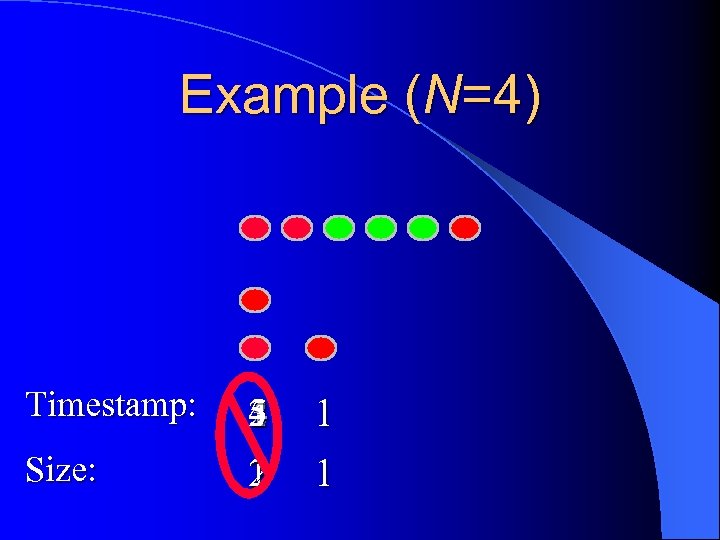
Example (N=4) Timestamp: Size: 5 4 3 2 1 1 1

(Timestamps are easy) Cyclic counter mod N. 9 10 11 12 13 14 0 6 5 4 3 2 1 01 0 N=15 14 0

What does the histogram buy us? l. Active bucket Contains an active 1. l. Only the last bucket might contain expired 1 s.

Estimating number of 1 s Conclusion: l T – sum of all bucket sizes but last. – So there at least T 1 s. l C – size of last bucket. – Actual # of 1 s can be anything from 1 to C.

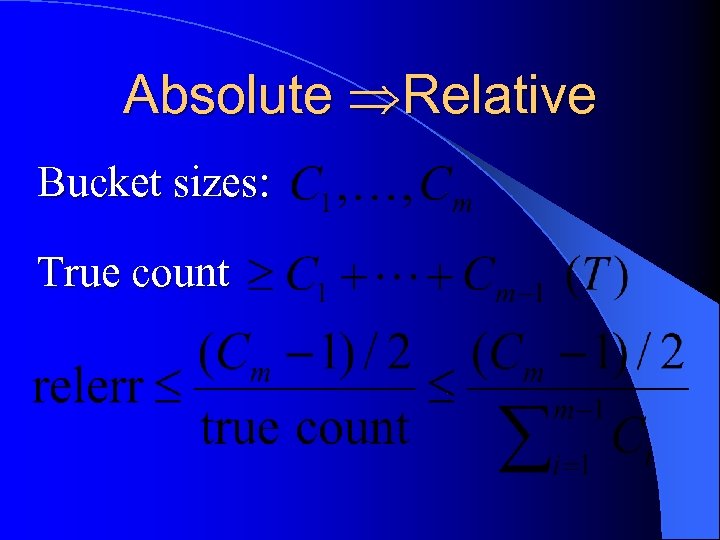
Absolute Relative Bucket sizes: True count

Bounding the error Goal: Relative error at most =1/k. If at all times we’d have that for all j,

How can we do that? (With as few buckets as Exponential possible? ) l. Non-decreasing bucket sizes. Histogram l. Bucket sizes constrained to l. At most buckets of each size. l. For all sizes but that of last bucket, at least buckets of each size.

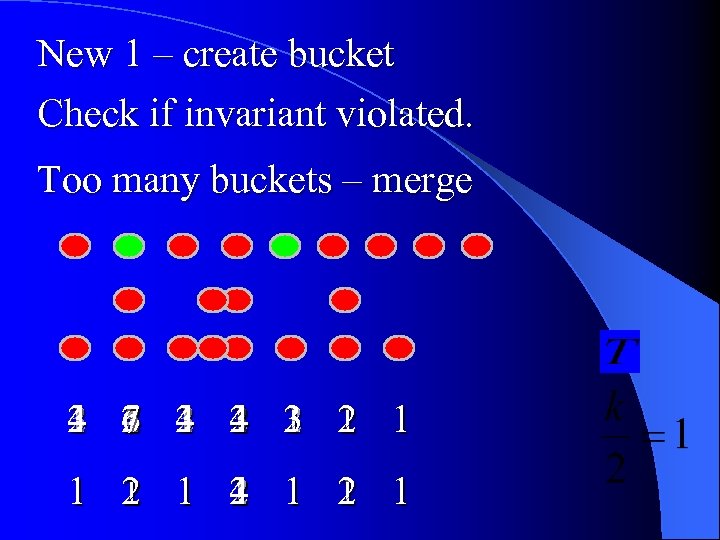
New 1 – create bucket Check if invariant violated. Too many buckets – merge 4 7 1 4 3 3 2 2 6 4 2 2 2 1 5 3 1 1 3 1 2 3 4 1 2 1 1 1 4 2 2

Why it works (correctness) If there at least buckets of sizes

Why it works (space) l. Can account for all 1 s with just

Space usage # of buckets: Bucket size: T counter for estimation:

Bucket of size B Sum of all Operations accounts for all buckets in life l. Estimation: O(1) operations related time l(including Cascading makes it BInsertion: to it: B inserts, 1 merges (& deleted) is allworst case. maybe delete). insertions. l. But only O(1) amortized! past

Plan üBasic Counting – Given a bit stream, maintain at every time instant the count of 1 s in the last N elements. l. Sum – Given an integer stream, maintain the sum of the last N elements. l. Everything else

n on ttiio err se ns IIn Extending to Sum l. Integers in range [0, R]. l. On value V, insert V 1 s. l. Timestamps: l. Bucket counter: l# of buckets: l. Total space: !! R)) ((R s es ke ak tta

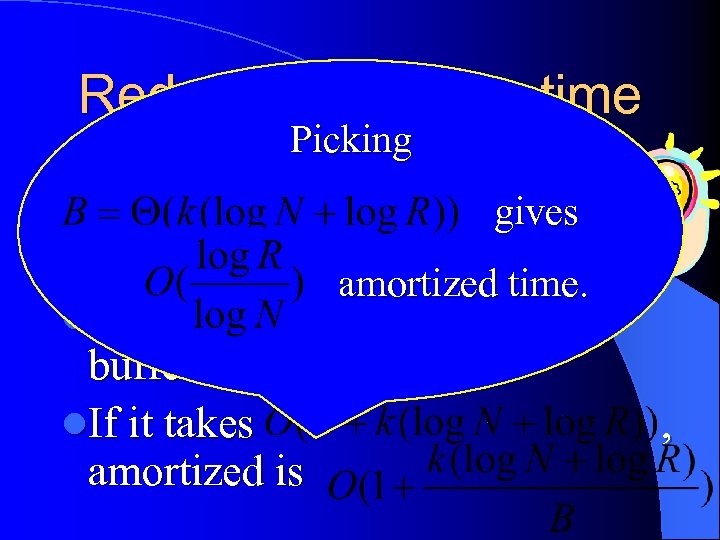
Reducing insertion time l. If we had a Picking rebuild the way to entire histogram… gives l. We could buffer new values… amortized time. l. And rebuild histogram when buffer reaches size B. l. If it takes , amortized is

Would it k/2 canonical really? representation Is this The k/2 canonical representation of S : representation unique? If S is the total size of the buckets, computing its k/2 canonical representation would help us rebuild the histogram.

Total time =01 Find the largest j for which required is O(log S). =5 If find j=2

8 6 4 3 2 1 10 7 5 4 3 2 9 8 6 5 4 3 If 2 value gets a “unindexed”, it will 5 never be indexed in the future. Calculate S 1+S 2 representation: 10 6 2 1 1

Plan • Lower Bounds üBasic Counting • More about timestamps. – Given a bit stream, maintain at every time instant the count of 1 s in the last N • Applications. elements. üSum. More problems • – Given an integer stream, maintain the sum of the last N elements. l. Everything else

• Lower Bounds Lower bounds • More about timestamps. • Applications. • More problems l. Basic Counting and Sum algorithms are optimal. l. Similar techniques will show that lots of other problems are intractable. (Later. )

Basic Counting bound N

Big block d Left most such subblock Same idea works for Sum.

Lower bound applies to randomized Randomized bound algorithms. l. Yao minimax principle: l. Expected space complexity of optimal algorithm for an input distribution is a lower bound on expected space complexity of randomized algorithm.

• Lower Bounds Timestamps • More about timestamps. • Applications. • More problems If much less than N items can arrive l. Define window based on real is during the window, memory usage time – equate timestamp with reduced. clock. l. No work needs to be done when items don’t arrive, so deletions can be deferred.

• Lower Bounds Applications • More about timestamps. • Applications. • More problems l. Adapting algorithms to the sliding window model using EH to replace counters. l. Counters require bits, EH takes. l. Also factor loss in accuracy.

• Lower Bounds More Problems • More about timestamps. • Applications. l. Min/Max • More problems – Storing subsequence of (say) mins is optimal. l. Distinct values – Basic Counting reduces to it.

Other Problems l. Distinct values with deletions. – Factor 2 estimation requires (N) space. – Map 1 s in a bit string to distinct values. Pad with zeros to infer value of last bit, then use deletion to cancel that bit. – Repeat.

Other Problems l. Sum with negative integers. – Factor 2 estimation requires (N) space. – Maps 1 s in bit string to (-1, 1) and 0 s to (1, -1). – Pad with 0 s and query at odd time instants.