23c40e7bfea25afac6cf0dc7d451e844.ppt
- Количество слайдов: 33

Magnetic Fields and MHD 17 February 2003 (snow permitting) Astronomy G 9001 - Spring 2003 Prof. Mordecai-Mark Mac Low

Mestel, Stellar Magnetism MHD Approximation • Maxwell’s Equations in a gas • This happens when thermal fluctuations can’t separate electrons, ions. • Balance TE to electric PE (Debye length) The displacement current vanishes if electrons & ions move together

Generalized Ohm’s Law Hall term • so long as ions are not very massive (eg dust grains) we may neglect the Hall term. • If σ large, then E+(v/c B) = 0

Induction Equation From Maxwell’s equations,

Lorentz Force • Ampère’s law, in absence of displacement current: • The Lorentz force density: • Remember vector identity: • so Lorentz force net force always acts perpendicular to B magnetic tension magnetic pressure

Magnetic Resistivity • If σ finite, then we can use Ohm’s law and Maxwell’s equations: Magnetic Reynolds #: magnetic diffusivity λ

Flux Conservation • If σ , then magnetic flux through any parcel of gas remains constant: d. S C • Gas remains tied to field lines

Flux Conservation Consequences • Flux cannot be created or destroyed without resistive effects (reconnection) • So where did Galactic field come from? • Flux carried with gas during collapse • How come stars do not have same mass to flux ratio as interstellar gas?

Jackson, Ch. 10 Classical Electrodynamics MHD Waves • Linearize MHD equations:


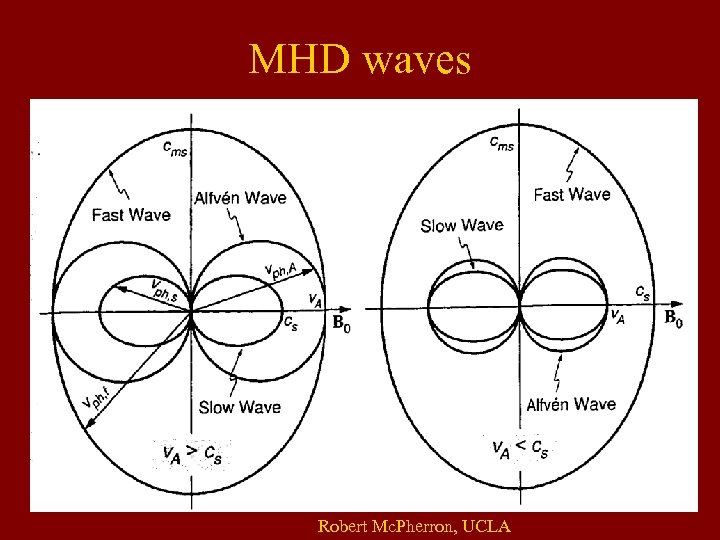
MHD waves Robert Mc. Pherron, UCLA

B 1 v 1 B 2 v 2 MHD Shocks Mestel, Stellar Magnetism • If B v then shock jump conditions are continuity of flux transport

MHD shock • perpendicular shock:

Oblique shocks • Field at arbitrary angle to shock normal • Parallel field must be conserved • Momentum conservation in frame w/ – no magnetic energy flow across shock • Momentum conservation then gives

Oblique Shocks • Three solutions (e. g. Mestel, p. 50): slow shock intermediate (Alfvèn) shock fast shock v 1

Partially Neutral Gas • Only ions feel Lorentz force from B field • Ions, neutrals couple through collisions, adding symmetric terms to momentum eqn
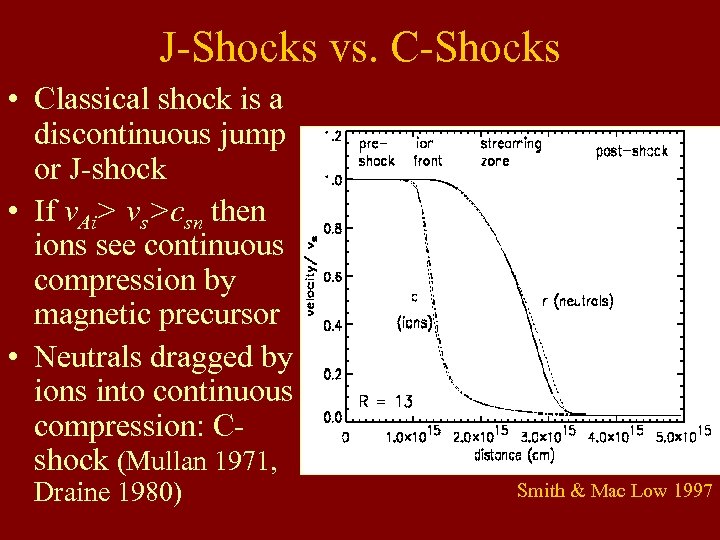
J-Shocks vs. C-Shocks • Classical shock is a discontinuous jump or J-shock • If v. Ai> vs>csn then ions see continuous compression by magnetic precursor • Neutrals dragged by ions into continuous compression: Cshock (Mullan 1971, Draine 1980) Smith & Mac Low 1997
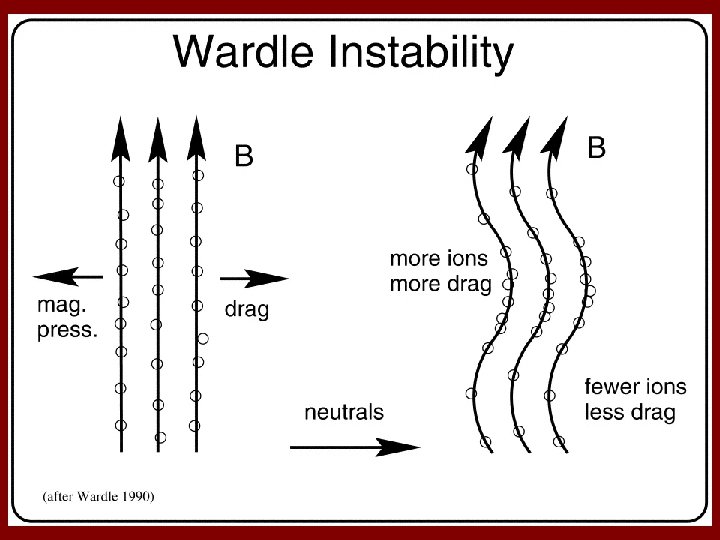
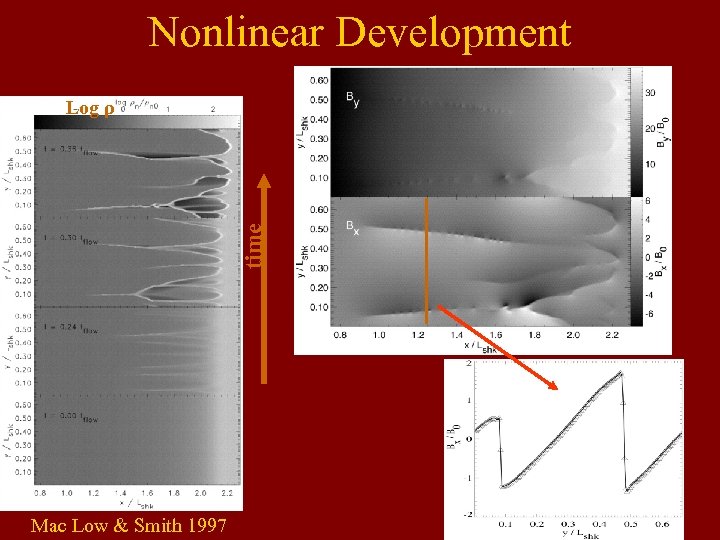
Nonlinear Development time Log ρ Mac Low & Smith 1997

Current Sheet Formation • Brandenburg & Zweibel (1994, 1995) showed that nonlinear nature of field diffusion from ion-neutral drift produces sharp structures. • Analogous to shock formation in strong sound waves: magnetic pressure higher in peaks, so waves spread and steepen. • Zweibel & Brandenburg (1997) emphasized that current sheets form, driving reconnection. • Seems to explain numerical results well.

Next week’s assignments • Read Slavin & Cox (1993, Ap. J, 417, 187) on the filling factor of hot gas with nonthermal pressures included • Read Stone & Norman (1992 b, Ap. JS, 80, 791) -- the MHD ZEUS paper • Complete the blast exercise

Parallelization • Additional issues: – How to coordinate multiple processors – How to minimize communications • Common types of parallel machines – shared memory, single program • eg SGI Origin 2000, dual or quad proc PCs – multiple memory, multiple program • eg Beowulf Linux clusters, Cray T 3 E, ASCI systems
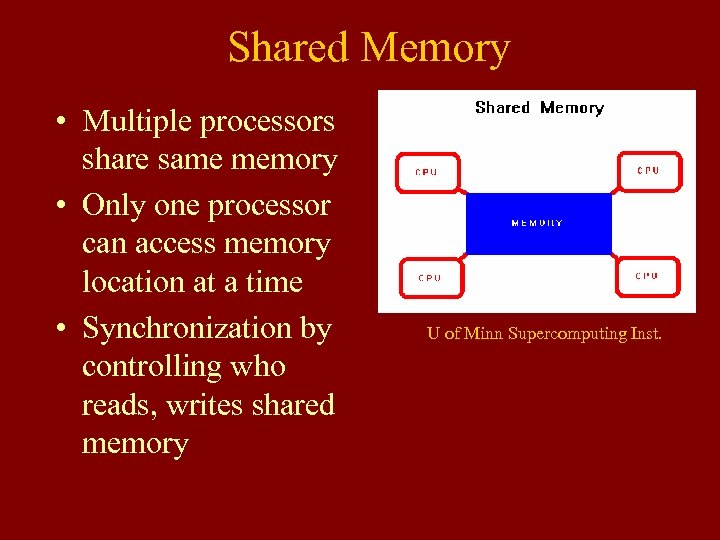
Shared Memory • Multiple processors share same memory • Only one processor can access memory location at a time • Synchronization by controlling who reads, writes shared memory U of Minn Supercomputing Inst.

Shared Memory • Advantages – Easy for user – Speed of memory access • Disadvantages – Memory bandwidth limited. – Increase of processors without increase of bandwidth will cause severe bottlenecks
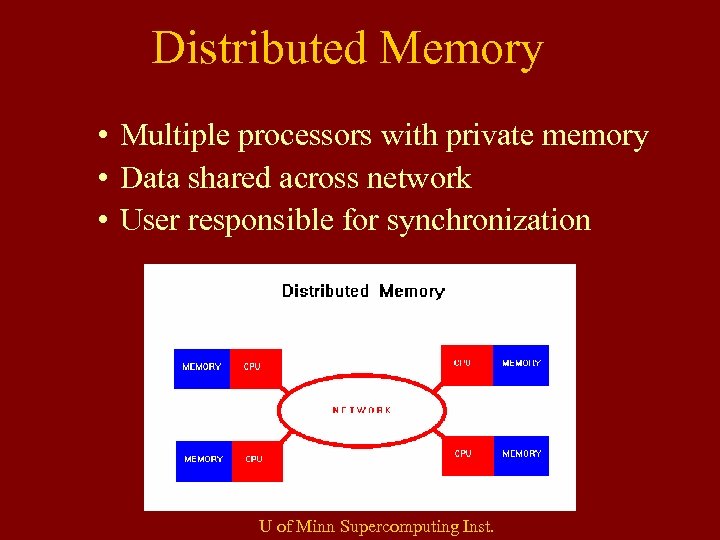
Distributed Memory • Multiple processors with private memory • Data shared across network • User responsible for synchronization U of Minn Supercomputing Inst.

Distributed Memory • Advantages – Memory scalable with number of processors. More processors, more memory. – Each processor can read its own memory quickly • Disadvantages – Difficult to map data structure to memory organization – User responsible for sending and receiving data among processors • To minimize overhead, data should be transferred early and in large chunks.

Methods • Shared memory – data parallel – loop level parallelization • Implementation – Open. MP – Fortran 90 – High Performance Fortran (HPF) • Examples – ZEUS-3 D • Distributed memory – block parallel – tiled grids • Implementation – Message Passing Interface (MPI) – Parallel Virtual Machine (PVM) • Examples – ZEUS-MP – Flashcode – GADGET

Open. MP • Designate inner loops that can be distributed across processors with DOACROSS command. • Dependencies between loop instances prevent parallelization • Execution of each loop usually depends on values from neighboring parts of grid. • ZEUS-3 D only parallelizes out to 8 -10 processors with Open. MP

Cache Optimization • Modern processors retrieve 64 bytes or more at a time from main memory – However it takes hundreds of cycles • Cache is small amount of very fast memory on microprocessor chip – Retrievals from cache take only a few cycles. • If successive operations can work on cached data, speed much higher – Fastest changing array index should be inner loop, even if code rearrangement required

Parallel ZEUS-3 D • To run ZEUS-3 D in parallel, set the variable iutask = 1 in setup block, recompile. – inserts DOACROSS directives – compiles with parallel flags turned on if OS supports them. • Set the number of processors for the job (usually with an environment variable) • Run is otherwise similar to serial.

Use of IDL • Quick and dirty movies pause for i=1, 30 do begin & $ a=sin(findgen(10000. )) & $ hdfrd, f=’zhd_’+string(i, form=’(i 3. 3)’)+’aa’, d=d, x=x & $ plot, x, d[4]. dat & end • Scaling, autoscaling, logscaling 2 D arrays tvscl, alog(d) tv, bytscl(d, max=dmax, min=dmin) • Array manipulation, resizing tvscl, rebin(d, nx, ny, /s) ; nx, ny multiple tvscl, rebin(reform(d[j, *, *]), nx, ny, /s)
![More IDL • plots, contours plot, x, d[i, *, k], xtitle=’Title’, psym=-3 oplot, x, More IDL • plots, contours plot, x, d[i, *, k], xtitle=’Title’, psym=-3 oplot, x,](https://present5.com/presentation/23c40e7bfea25afac6cf0dc7d451e844/image-33.jpg)
More IDL • plots, contours plot, x, d[i, *, k], xtitle=’Title’, psym=-3 oplot, x, d[i+10, *, k] contour, reform(d[i, *, *]), nlev=10 • slicer 3 D dp = ptr_new(alog 10(d)) slicer 3 D, dp • Subroutines, functions
23c40e7bfea25afac6cf0dc7d451e844.ppt