Магистерский проект Simultaneous localization and mapping Магистрант Матрунич

Магистерский проект Simultaneous localization and mapping Магистрант: Матрунич Сергей Анатольевич Научный руководитель: Зимянин Л. Ф. 2008

Краткое содержание Ø Введение Ø SLAM используя фильтр Калмана Ø SLAM используя фильтр для частиц Ø Исследование : проблема поиска

Введение: SLAM: Simultaneous Localization and Mapping Робот изучает незнакомое, статическое окружение. Дано: § Система управления роботом § Визуальные датчики Оба источника данных зашумлены. Оценка: § Положения робота -- localization где Я ? § Детализация окружающего пространства – mapping На что похоже то что вокруг меня?

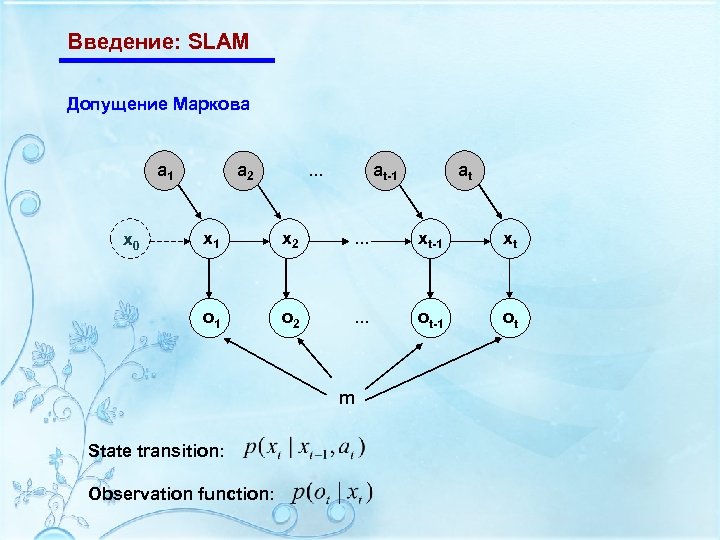Введение: SLAM Допущение Маркова a 1 a 2 at at-1 … x 1 x 2 … xt-1 xt o 1 x 0 o 2 … ot-1 ot m State transition: Observation function:

Введение: SLAM Method: Sequentially estimate the probability distribution p(xt) and update the map. Prior: p(x 0) p(x 1) p(m 1) or m 1 … p(xt-1) p(mt-1) or mt-1 p(xt) p(mt) or mt Prior distribution on xt after taking action at

Введение: SLAM Методы: The robot’s trajectory estimate is a tracking problem 1. Parametric method – Kalman filter Represent the distribution of robot location xt (and map mt ) by a Normal distribution Sequentially update μt and Σt 2. Sample-based method – particle filter Represent the distribution of robot location xt (and map mt) by a large amount of simulated samples. Resample xt (and mt) at each time step

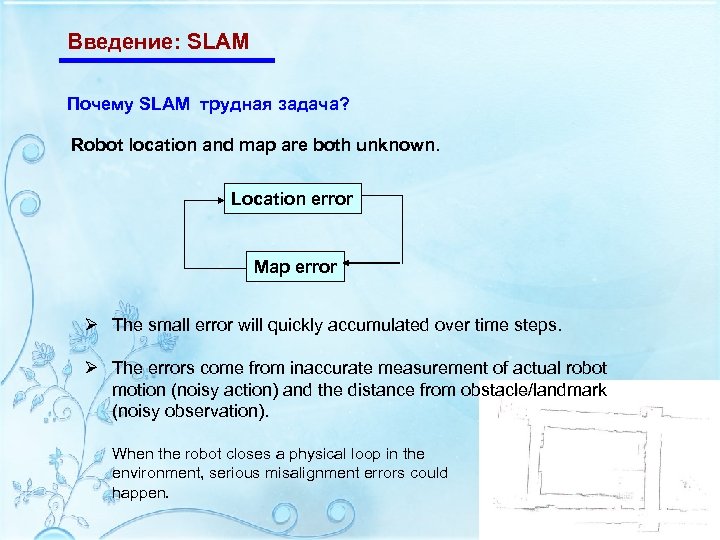Введение: SLAM Почему SLAM трудная задача? Robot location and map are both unknown. Location error Map error Ø The small error will quickly accumulated over time steps. Ø The errors come from inaccurate measurement of actual robot motion (noisy action) and the distance from obstacle/landmark (noisy observation). When the robot closes a physical loop in the environment, serious misalignment errors could happen.

SLAM: фильтр Калмана Корректирующее уровнение: Предположение: Prior p(x 0) is a normal distribution Observation function p(o|x) is a normal distribution Тогда: Posterior p(x 1), …, p(xt) are all normally distributed. Mean μt and covariance matrix Σt can be derived analytically. Sequentially update μt and Σt for each time step t

SLAM: фильтр Калмана Assume: State transition Observation function Kalman filter: Propagation (motion model): Update (sensor model):

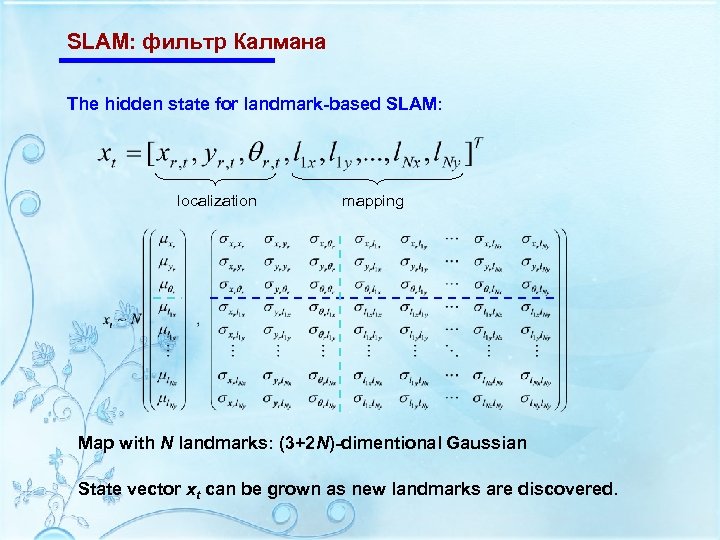SLAM: фильтр Калмана The hidden state for landmark-based SLAM: localization mapping Map with N landmarks: (3+2 N)-dimentional Gaussian State vector xt can be grown as new landmarks are discovered.

SLAM: фильтр для частиц Update equation: Основная идея: Ø Normal distribution assumption in Kalman filter is not necessary Ø A set of samples approximates the posterior distribution and will be used at next iteration. Ø Each sample maintains its own map; or all samples maintain a single map. Ø The map(s) is updated upon observation, assuming that the robot location is given correctly.

SLAM: фильтр для частиц Particle filter: Assume it is difficult to sample directly from But get samples from another distribution We sample for each xit as from The set of Resample xt from with uniform weights is easy. , with normalized weight (particles) is an approximation of , with replacement, to get a sample set

SLAM: фильтр для частиц Particle filter (cont’d): 0. 4 0. 3 0. 2 0. 1

SLAM: фильтр для частиц Choose appropriate Choose Transition probability Then Observation function

SLAM: фильтр для частиц Алгоритм: Let state xt represent the robot’s location, 1. Propagate each state through the state transition probability . This samples a new state 2. Weight each new state given the previous state. according to the observation function 3. Normalize the weights, get 4. Resampling: sample Ns new states . from are the updated robot location from

SLAM: фильтр для частиц State transition probability: are the expected robot moving distance (angle) by taking action at. Observation probability: Measured distance (observation) for sensor k Map distance from location xt to the obstacle

SLAM: фильтр для частиц Lots of work on SLAM using particle filter are focused on: Ø Reducing the cumulative error Ø Fast SLAM (online) Ø Way to organize the data structure (saving robot path and map). Maintain single map: cumulative error Multiple maps: memory and computation time In Parr’s paper: Ø Use ancestry tree to record particle history Ø Each particle has its own map (multiple maps) Ø Use observation tree for each grid square (cell) to record the map corresponding to each particle. Ø Update ancestry tree and observation tree at each iteration. Ø Cell occupancy is represented by a probabilistic approach.

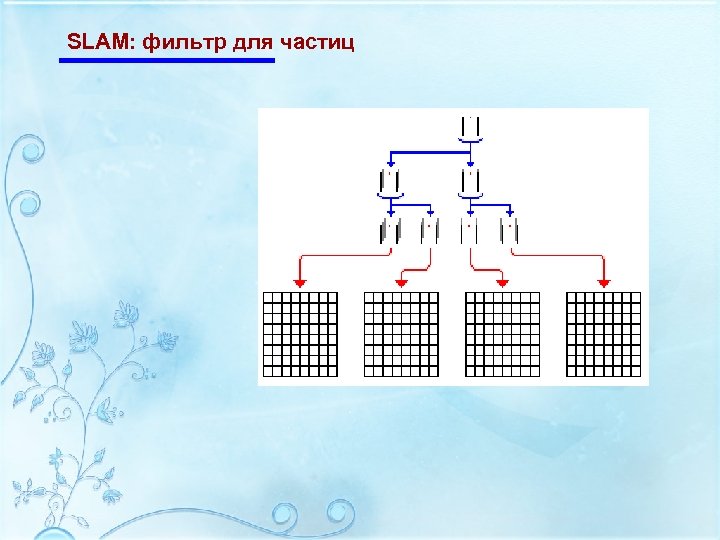SLAM: фильтр для частиц

Проблема поиска Assumption: Ø The agent doesn’t have map, doesn’t know the underlying model, doesn’t know where the target is. Ø Agent has 2 sensors: ü Camera: tell agent “occupied” or “empty” cells in 4 orientations, noisy sensor. ü Acoustic sensor: find the orientation of the target, effective only within certain distance. Ø Noisy observation, noisy action.

Проблема поиска Similar to SLAM Ø To find the target, agent need build map and estimate its location. Differences from SLAM Ø Rough map is enough; an accurate map is not necessary. Ø Objective is to find the target. Robot need to actively select actions to find the target as soon as possible.

Проблема поиска Model: Ø Environment is represented by a rough grid; Ø Each grid square (state) is either occupied or empty. Ø The agent moves between the empty grid squares. Ø Actions: walk to any one of the 4 directions, or “stay”. Could fail in walking with certain probability. Ø Observations: observe 4 orientations of its neighbor grid squares: “occupied” or “empty”. Could make a wrong observation with certain probability. Ø State, action and observation are all discrete.

Проблема поиска In each step, the agent updates its location and map: Ø Belief state: the agent believes which state it is currently in. It is a distribution over all the states in the current map. Ø The map: The agent thinks what the environment is. üFor each state (grid square), a 2 -dimentional Dirichlet distribution is used to represent the probability of “empty” and “occupied”. üThe hyperparameters of Dirichlet distribution are updated based on current observation and belief state.

Проблема поиска Belief state update: the set of neighbor states of s where Probability of successful moving from sj to s when taking action a and with Neighbor of s in orientation j From map representation

Проблема поиска Обновление карты (распределение Дирихле): Предпологаем на шаге t-1, гиперпараметр для S На шаге t, гиперпараметр для S обновляется до and are the posterior after observing o given that the agent is in the neighbor of state s. If the probability of wrong observation for any orientation is p 0, then p 0 if o is “occupied” 1 -p 0 if o is “empty” prior can be computed similarly.

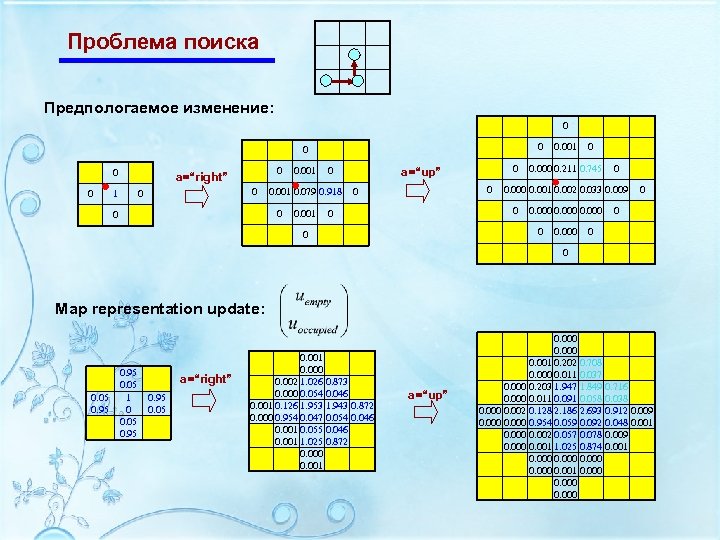Проблема поиска Предпологаемое изменение: 0 0 0 a=“right” 1 0 0 0. 001 0 a=“up” 0 0. 001 0. 079 0. 918 0 0 0. 001 0 0 0. 000 0. 211 0. 745 0. 000 0 0 0. 001 0. 002 0. 033 0. 009 0 0 0. 001 0. 000 0 0 Map representation update: 0. 05 0. 95 0. 05 1 0 0. 05 0. 95 a=“right” 0. 95 0. 001 0. 000 0. 002 1. 026 0. 873 0. 000 0. 054 0. 046 0. 001 0. 126 1. 953 1. 943 0. 872 0. 000 0. 954 0. 047 0. 054 0. 046 0. 001 0. 055 0. 046 0. 001 1. 025 0. 872 0. 000 0. 001 a=“up” 0. 000 0. 001 0. 202 0. 708 0. 000 0. 011 0. 037 0. 000 0. 203 1. 947 1. 849 0. 000 0. 011 0. 091 0. 058 0. 000 0. 002 0. 128 2. 186 2. 693 0. 000 0. 954 0. 059 0. 092 0. 000 0. 002 0. 057 0. 078 0. 000 0. 001 1. 025 0. 874 0. 000 0. 001 0. 000 0. 716 0. 038 0. 912 0. 009 0. 048 0. 001 0. 009 0. 001

Проблема поиска Выберите действие: Each state is assigned a reward R(s) according to following rules: Less explored grids have higher reward. Try to walk to the “empty” grid square. Consider neighbor of s with priority. x x

Cпасибо за внимание