MA CSSE 474 Theory of Computation Pushdown Automata PDA

MA/CSSE 474 Theory of Computation Pushdown Automata (PDA) Intro

Your Questions? • Previous class days' material • Reading Assignments • HW 10 problems • Anything else

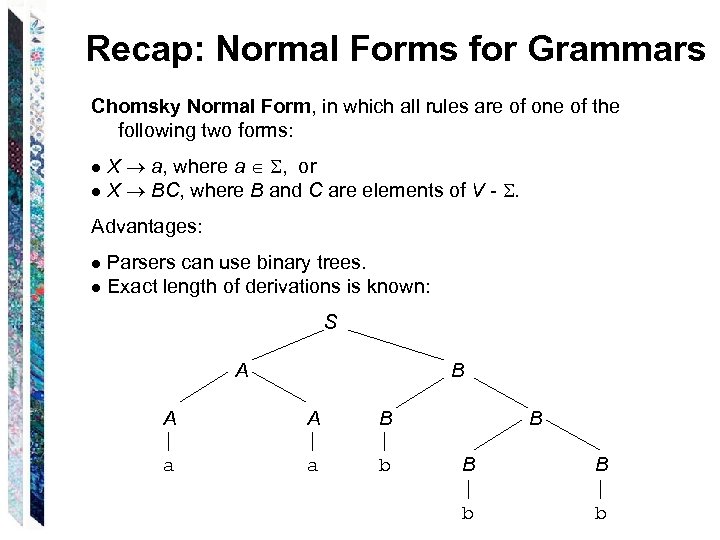Recap: Normal Forms for Grammars Chomsky Normal Form, in which all rules are of one of the following two forms: ● X a, where a , or ● X BC, where B and C are elements of V - . Advantages: ● Parsers can use binary trees. ● Exact length of derivations is known: S A B A A B a a b B B B b b

Recap: Normal Forms for Grammars Greibach Normal Form, in which all rules are of the following form: ● X a , where a and (V - )*. Advantages: ● Every derivation of a string s contains |s| rule applications. ● Greibach normal form grammars can easily be converted to pushdown automata with no transitions. This is useful because such PDAs are guaranteed to halt.

Theorems: Normal Forms Exist Theorem: Given a CFG G, there exists an equivalent Chomsky normal form grammar GC such that: L(GC) = L(G) – { }. Proof: The proof is by construction. Details of Chomsky conversion are complex but straightforward; I leave them for you to read in Chapter 11 and/or in the next 16 slides. Theorem: Given a CFG G, there exists an equivalent Greibach normal form grammar GG such that: Details of Greibach conversion are more L(GG) = L(G) – { }. complex but still straightforward; I leave Proof: The proof is also by construction. them for you to read in Appendix D if you wish (not req'd).

The Price of Normal Forms E E + E E (E) E id Converting to Chomsky normal form: E E E E P E E L E E E R E id L ( R ) P + Conversion doesn’t change weak generative capacity but it may change strong generative capacity.

Pushdown Automata

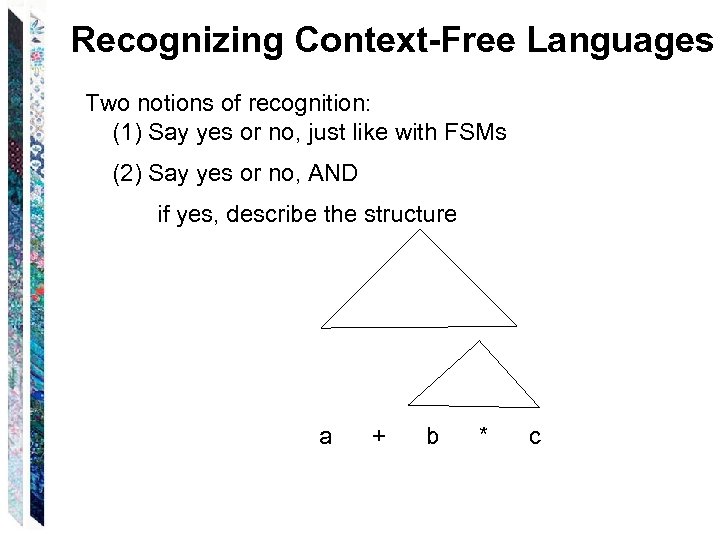Recognizing Context-Free Languages Two notions of recognition: (1) Say yes or no, just like with FSMs (2) Say yes or no, AND if yes, describe the structure a + b * c

Definition of a Pushdown Automaton M = (K, , s, A), where: K is a finite set of states is the input alphabet and are not is the stack alphabet necessarily disjoint s K is the initial state A K is the set of accepting states, and is the transition relation. It is a finite subset of (K ( { }) *) (K *) state input or string of state symbols to pop from top of stack string of symbols to push on top of stack

Definition of a Pushdown Automaton A configuration of M is an element of K * *. The initial configuration of M is (s, w, ), where w is the input string.

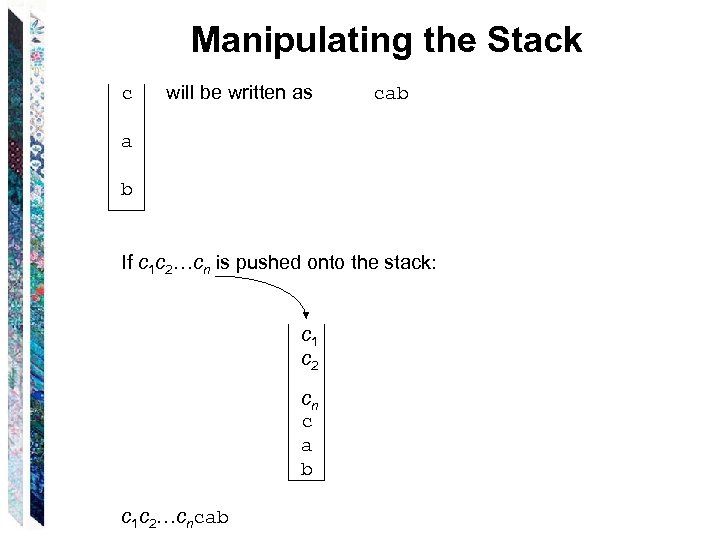Manipulating the Stack c will be written as cab a b If c 1 c 2…cn is pushed onto the stack: c 1 c 2 cn c a b c 1 c 2…cncab

Yields Let c be any element of { }, Let 1, 2 and be any elements of *, and Let w be any element of *. Then: (q 1, cw, 1 ) |-M (q 2, w, 2 ) iff ((q 1, c, 1), (q 2, 2)) . Let |-M* be the reflexive, transitive closure of |-M. C 1 yields configuration C 2 iff C 1 |-M* C 2

Computations A computation by M is a finite sequence of configurations C 0, C 1, …, Cn for some n 0 such that: ● C 0 is an initial configuration, ● Cn is of the form (q, , ), for some state q KM and some string in *, and ● C 0 |-M C 1 |-M C 2 |-M … |-M Cn.

Nondeterminism If M is in some configuration (q 1, s, ) it is possible that: ● contains exactly one transition that matches. ● contains more than one transition that matches. ● contains no transition that matches.

Accepting A computation C of M is an accepting computation iff: ● C = (s, w, ) |-M* (q, , ), and ● q A. M accepts a string w iff at least one of its computations accepts. Other paths may: ● Read all the input and halt in a nonaccepting state, ● Read all the input and halt in an accepting state with the stack not empty, ● Loop forever and never finish reading the input, or ● Reach a dead end where no more input can be read. The language accepted by M, denoted L(M), is the set of all strings accepted by M.

Rejecting A computation C of M is a rejecting computation iff: ● C = (s, w, ) |-M* (q, w , ), ● C is not an accepting computation, and ● M has no moves that it can make from (q, , ). M rejects a string w iff all of its computations reject. Note that it is possible that, on input w, M neither accepts nor rejects.

A PDA for Bal M = (K, , s, A), where: K = {s} the states = {(, )} the input alphabet = {(} the stack alphabet A = {s} contains: ((s, (, ), (s, ( )) ** ((s, ), (s, )) **Important: This does not mean that the stack is empty

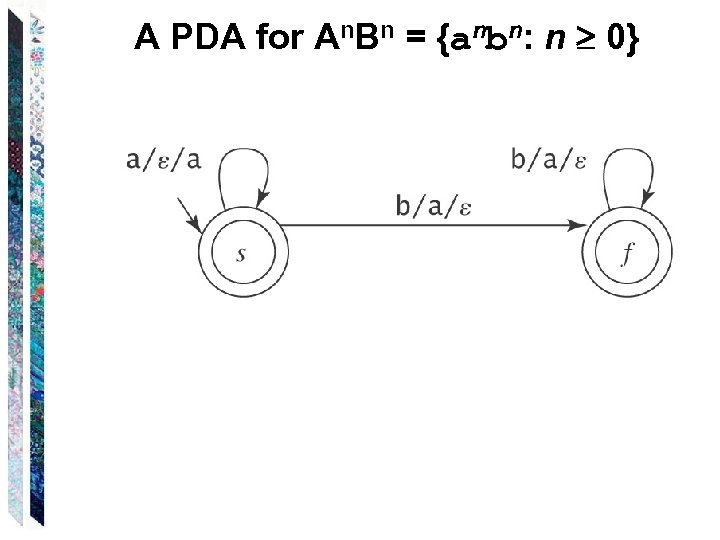A PDA for An. Bn = {anbn: n 0}

A PDA for {wcw. R: w {a, b}*} M = (K, , s, A), where: K = {s, f} the states = {a, b, c} the input alphabet = {a, b} the stack alphabet A = {f} the accepting states contains: ((s, a, ), (s, a)) ((s, b, ), (s, b)) ((s, c, ), (f, )) ((f, a, a), (f, )) ((f, b, b), (f, ))

A PDA for {anb 2 n: n 0}

A PDA for Pal. Even ={ww. R: w {a, b}*} S S a. Sa S b. Sb A PDA: This one is nondeterministic

A PDA for {w {a, b}* : #a(w) = #b(w)}

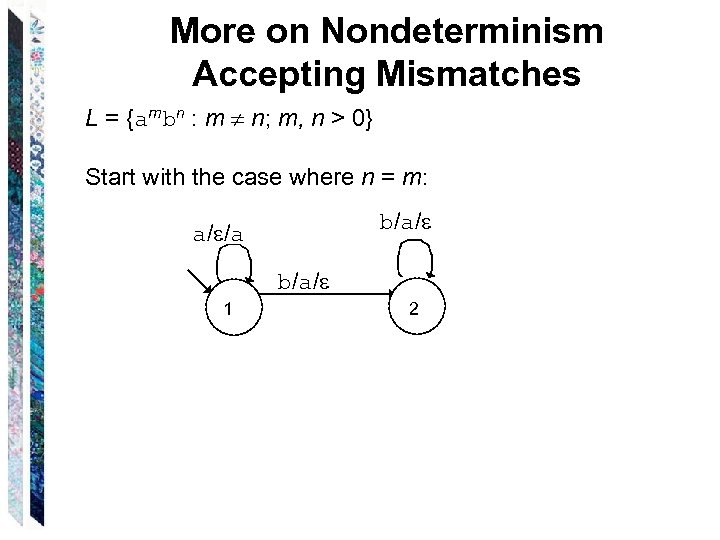More on Nondeterminism Accepting Mismatches L = {ambn : m n; m, n > 0} Start with the case where n = m: b/a/ a/ /a b/a/ 1 2

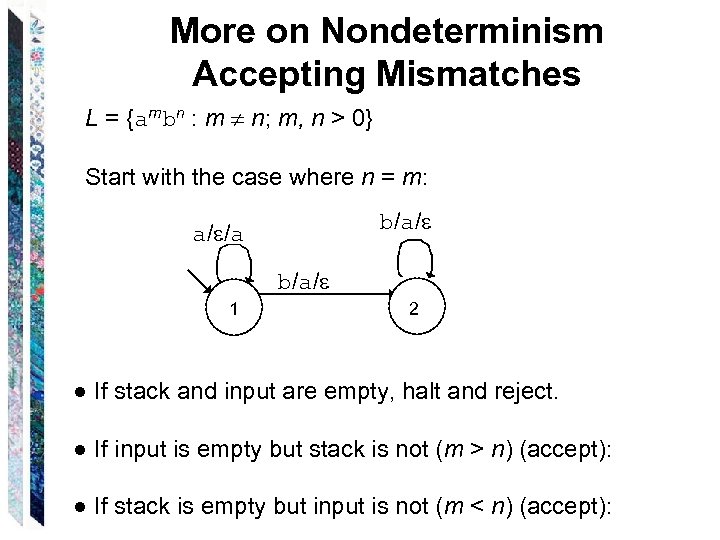More on Nondeterminism Accepting Mismatches L = {ambn : m n; m, n > 0} Start with the case where n = m: b/a/ a/ /a b/a/ 1 2 ● If stack and input are empty, halt and reject. ● If input is empty but stack is not (m > n) (accept): ● If stack is empty but input is not (m < n) (accept):

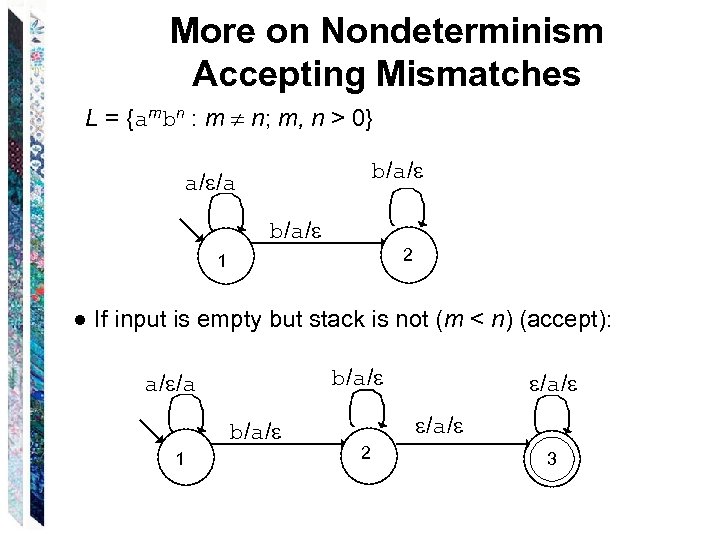More on Nondeterminism Accepting Mismatches L = {ambn : m n; m, n > 0} b/a/ a/ /a b/a/ 2 1 ● If input is empty but stack is not (m < n) (accept): b/a/ a/ /a b/a/ 1 /a/ 2 3

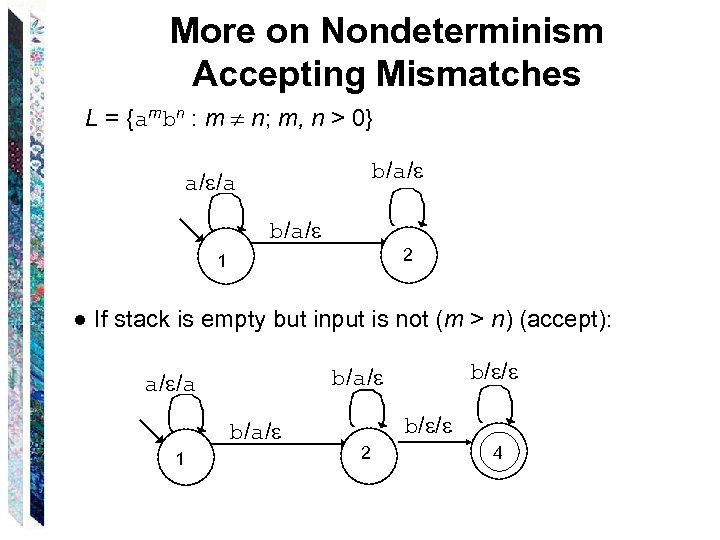More on Nondeterminism Accepting Mismatches L = {ambn : m n; m, n > 0} b/a/ a/ /a b/a/ 2 1 ● If stack is empty but input is not (m > n) (accept): b/a/ 1 b/ / b/a/ a/ /a b/ / 2 4

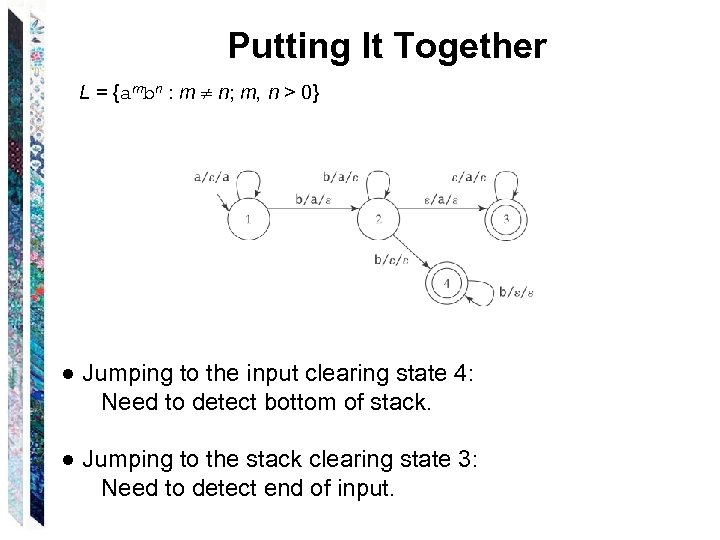Putting It Together L = {ambn : m n; m, n > 0} ● Jumping to the input clearing state 4: Need to detect bottom of stack. ● Jumping to the stack clearing state 3: Need to detect end of input.

The Power of Nondeterminism Consider An. Bn. Cn = {anbncn: n 0}. PDA for it?

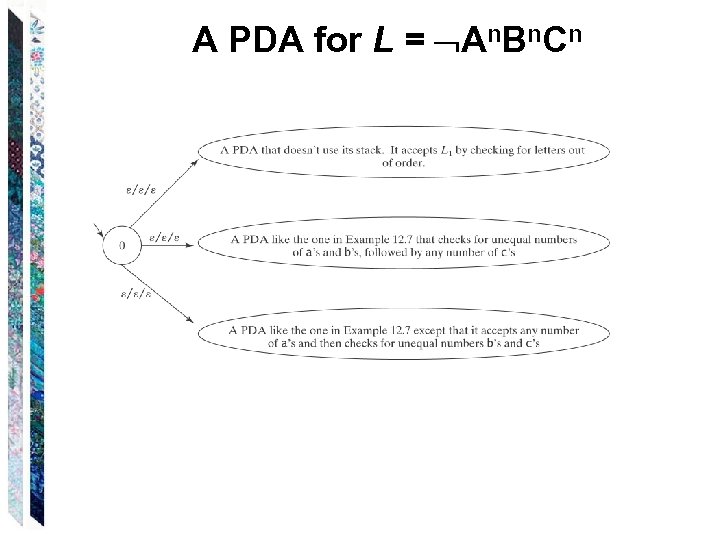
The Power of Nondeterminism Consider An. Bn. Cn = {anbncn: n 0}. Now consider L = An. Bn. Cn. L is the union of two languages: 1. {w {a, b, c}* : the letters are out of order}, and 2. {aibjck: i, j, k 0 and (i j or j k)} (in other words, unequal numbers of a’s, b’s, and c’s).

A PDA for L = An. Bn. Cn

Are the Context-Free Languages Closed Under Complement? An. Bn. Cn is context free. If the CF languages were closed under complement, then An. Bn. Cn = An. Bn. Cn would also be context-free. But we will prove that it is not.

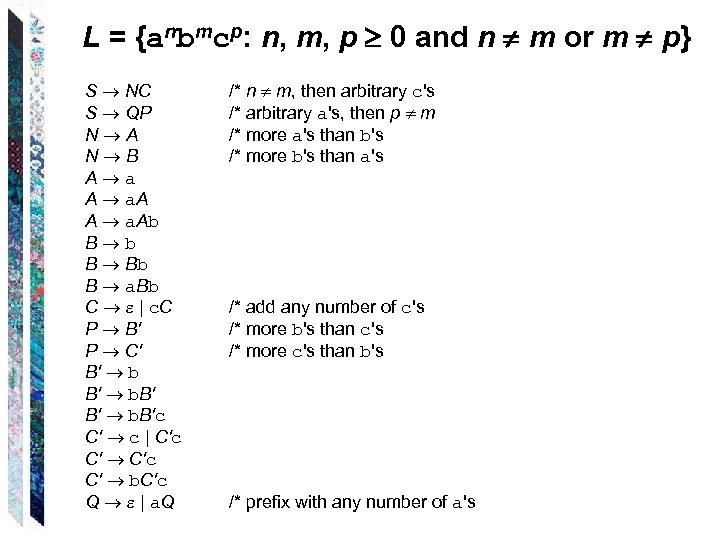L = {anbmcp: n, m, p 0 and n m or m p} S NC S QP N A N B A a. Ab B Bb B a. Bb C | c. C P B' P C' B' b. B'c C' c | C'c C' b. C'c Q | a. Q /* n m, then arbitrary c's /* arbitrary a's, then p m /* more a's than b's /* more b's than a's /* add any number of c's /* more b's than c's /* more c's than b's /* prefix with any number of a's

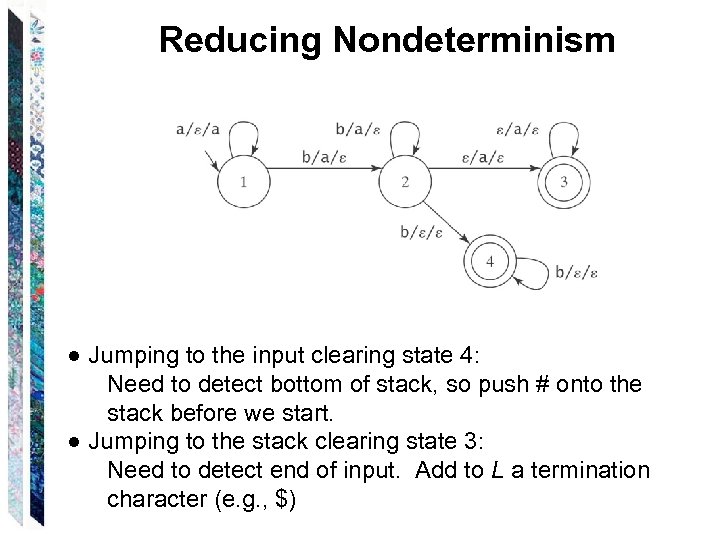Reducing Nondeterminism ● Jumping to the input clearing state 4: Need to detect bottom of stack, so push # onto the stack before we start. ● Jumping to the stack clearing state 3: Need to detect end of input. Add to L a termination character (e. g. , $)

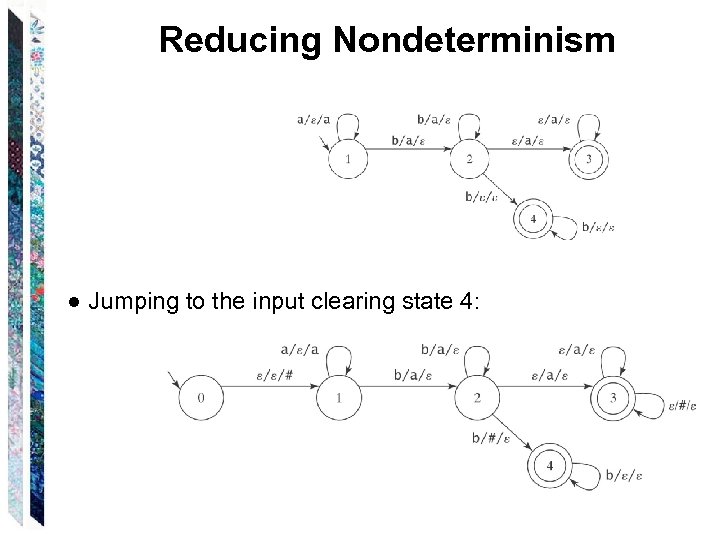Reducing Nondeterminism ● Jumping to the input clearing state 4:

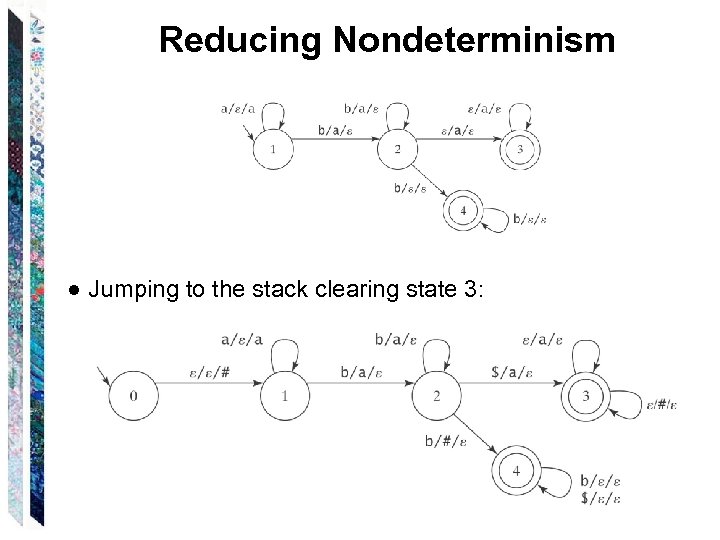Reducing Nondeterminism ● Jumping to the stack clearing state 3:

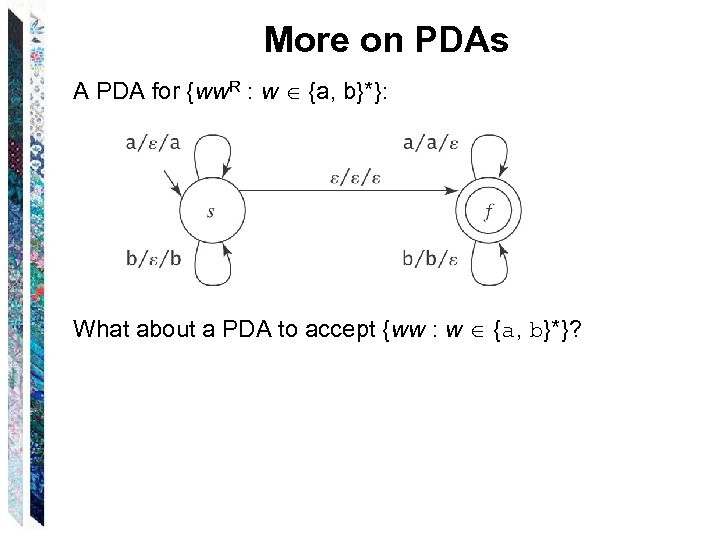More on PDAs A PDA for {ww. R : w {a, b}*}: What about a PDA to accept {ww : w {a, b}*}?

PDAs and Context-Free Grammars Theorem: The class of languages accepted by PDAs is exactly the class of context-free languages. Recall: context-free languages are languages that can be defined with context-free grammars. Restate theorem: Can describe with context-free grammar Can accept by PDA

Going One Way Lemma: Each context-free language is accepted by some PDA. Proof (by construction): The idea: Let the stack do the work. Two approaches: • Top down • Bottom up

Top Down The idea: Let the stack keep track of expectations. Example: Arithmetic expressions E E + T E T T T F F (E) F id (1) (q, , E), (q, E+T) (2) (q, , E), (q, T) (3) (q, , T), (q, T*F) (4) (q, , T), (q, F) (5) (q, , F), (q, (E) ) (6) (q, , F), (q, id) (7) (q, id), (q, ) (8) (q, (, ( ), (q, ) (9) (q, ), ) ), (q, ) (10) (q, +, +), (q, ) (11) (q, , ), (q, )

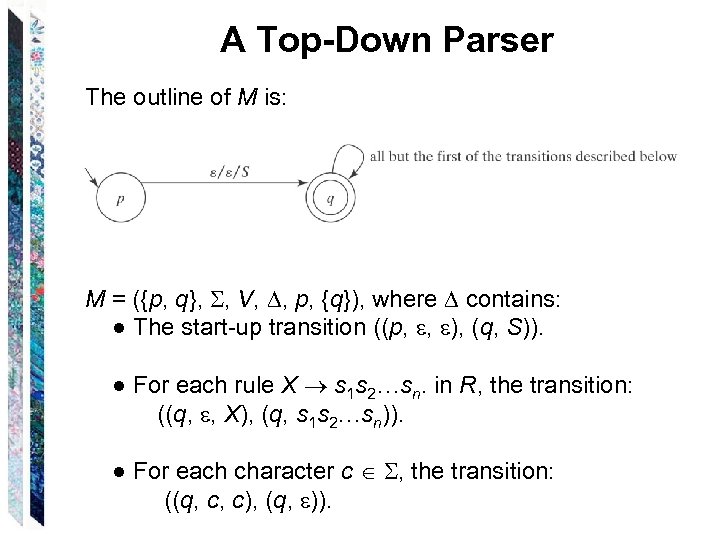A Top-Down Parser The outline of M is: M = ({p, q}, , V, , p, {q}), where contains: ● The start-up transition ((p, , ), (q, S)). ● For each rule X s 1 s 2…sn. in R, the transition: ((q, , X), (q, s 1 s 2…sn)). ● For each character c , the transition: ((q, c, c), (q, )).

Example of the Construction L = {anb*an} (1) S * (2) S B (3) S a. Sa (4) B (5) B b. B input = a a b b a a trans 0 3 6 2 5 7 4 6 6 state p q q q q 0 (p, , ), (q, S) 1 (q, , S), (q, ) 2 (q, , S), (q, B) 3 (q, , S), (q, a. Sa) 4 (q, , B), (q, ) 5 (q, , B), (q, b. B) 6 (q, a, a), (q, ) 7 (q, b, b), (q, ) unread input a a b b a a a b b a a b a a a stack S a. Sa Sa a. Saa Baa b. Baa Baa aa a

Another Example L = {anbmcpdq : m + n = p + q} (1) S a. Sd (2) S T (3) S U (4) T a. Tc (5) T V (6) U b. Ud (7) U V (8) V b. Vc (9) V input = a a b c d d

Another Example L = {anbmcpdq : m + n = p + q} 0 (p, , ), (q, S) (1) S a. Sd 1 (q, , S), (q, a. Sd) (2) S T 2 (q, , S), (q, T) (3) S U 3 (q, , S), (q, U) (4) T a. Tc 4 (q, , T), (q, a. Tc) (5) T V 5 (q, , T), (q, V) (6) U b. Ud 6 (q, , U), (q, b. Ud) (7) U V 7 (q, , U), (q, V) (8) V b. Vc 8 (q, , V), (q, b. Vc) (9) V 9 (q, , V), (q, ) 10 (q, a, a), (q, ) 11 (q, b, b), (q, ) input = a a b c d d 12 (q, c, c), (q, ) 13 (q, d, d), (q, ) trans state unread input stack

The Other Way to Build a PDA - Directly L = {anbmcpdq : m + n = p + q} (1) S a. Sd (2) S T (3) S U (4) T a. Tc (5) T V input = a a b c d d (6) U b. Ud (7) U V (8) V b. Vc (9) V

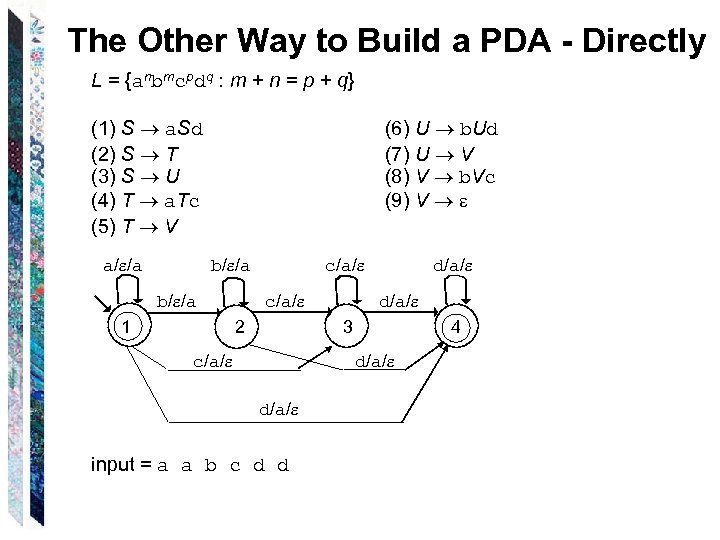The Other Way to Build a PDA - Directly L = {anbmcpdq : m + n = p + q} (1) S a. Sd (2) S T (3) S U (4) T a. Tc (5) T V a/ /a (6) U b. Ud (7) U V (8) V b. Vc (9) V b/ /a 1 c/a/ 2 d/a/ 3 c/a/ 4 d/a/ input = a a b c d d

Notice Nondeterminism Machines constructed with the algorithm are often nondeterministic, even when they needn't be. This happens even with trivial languages. Example: An. Bn = {anbn: n 0} A grammar for An. Bn is: [1] S a. Sb [2] S A PDA M for An. Bn is: (0) ((p, , ), (q, S)) (1) ((q, , S), (q, a. Sb)) (2) ((q, , S), (q, )) (3) ((q, a, a), (q, )) (4) ((q, b, b), (q, )) But transitions 1 and 2 make M nondeterministic. A directly constructed machine for An. Bn:

Bottom-Up The idea: Let the stack keep track of what has been found. (1) E E + T (2) E T (3) T T F (4) T F (5) F (E) (6) F id Reduce Transitions: (1) (p, , T + E), (p, E) (2) (p, , T), (p, E) (3) (p, , F T), (p, T) (4) (p, , F), (p, T) (5) (p, , )E( ), (p, F) (6) (p, , id), (p, F) Shift Transitions (7) (p, id, ), (p, id) (8) (p, (, ), (p, () (9) (p, ), (p, )) (10) (p, +, ), (p, +) (11) (p, , ), (p, )

A Bottom-Up Parser The outline of M is: M = ({p, q}, , V, , p, {q}), where contains: ● The shift transitions: ((p, c, ), (p, c)), for each c . ● The reduce transitions: ((p, , (s 1 s 2…sn. )R), (p, X)), for each rule X s 1 s 2…sn. in G. ● The finish up transition: ((p, , S), (q, )).