M-метод Лекция 3 Вопросы Использование дополнительных

M-метод Лекция № 3

Вопросы Использование дополнительных переменных Использование искусственных переменных М-метод Двухэтапный метод

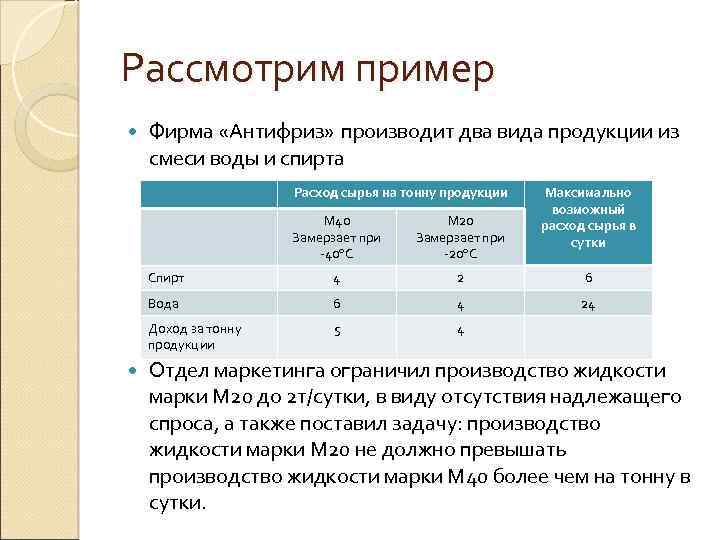Рассмотрим пример Фирма «Антифриз» производит два вида продукции из смеси воды и спирта Расход сырья на тонну продукции Максимально возможный расход сырья в сутки М 40 Замерзает при -40 С Спирт 4 2 6 Вода 6 4 24 Доход за тонну продукции М 20 Замерзает при -20 С 5 4 Отдел маркетинга ограничил производство жидкости марки М 20 до 2 т/сутки, в виду отсутствия надлежащего спроса, а также поставил задачу: производство жидкости марки М 20 не должно превышать производство жидкости марки М 40 более чем на тонну в сутки.

Формализуем пример Введем обозначения: x 1 – объем производимой жидкости марки М 40, x 2 – объем производимой жидкости марки М 20. Целевая функция: f = 5 x 1 + 4 x 2 max Ограничения: 4 x 1 + 2 x 2 6 6 x 1 + 4 x 2 2 -x 1 + x 2 1 x 1 , x 2 0

Представим задачу в канонической форме Откуда легко получить допустимый вид задачи

Проблемный пример Исходная задача Каноническая задача Видим, что допустимый вид получить не так просто как раньше

М-метод Введем в ограничения и в целевую функцию искусственные переменные И используем их в качестве недостающих базисных

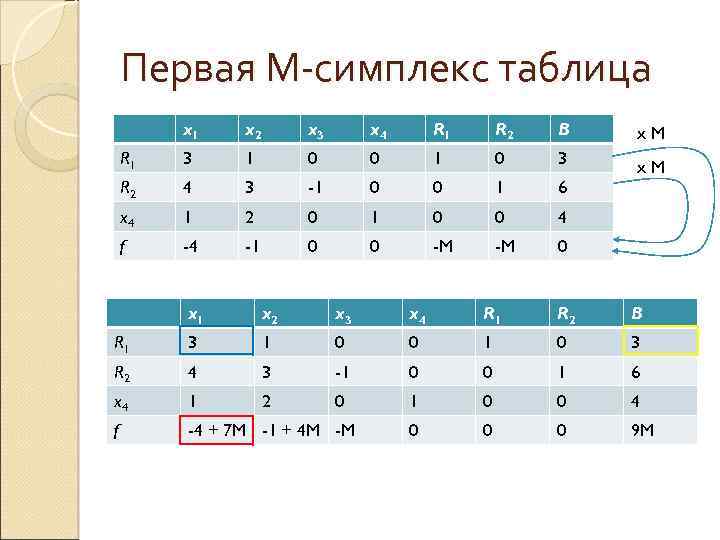Первая М-симплекс таблица x 1 x 2 x 3 x 4 R 1 R 2 B x. M R 1 3 1 0 0 1 0 3 R 2 4 3 -1 0 0 1 6 x. M x 4 1 2 0 1 0 0 4 f -4 -1 0 0 -M -M 0 x 1 x 2 x 3 x 4 R 1 R 2 B R 1 3 1 0 0 1 0 3 R 2 4 3 -1 0 0 1 6 x 4 1 2 0 1 0 0 4 f -4 + 7 M -1 + 4 M -M 0 0 0 9 M

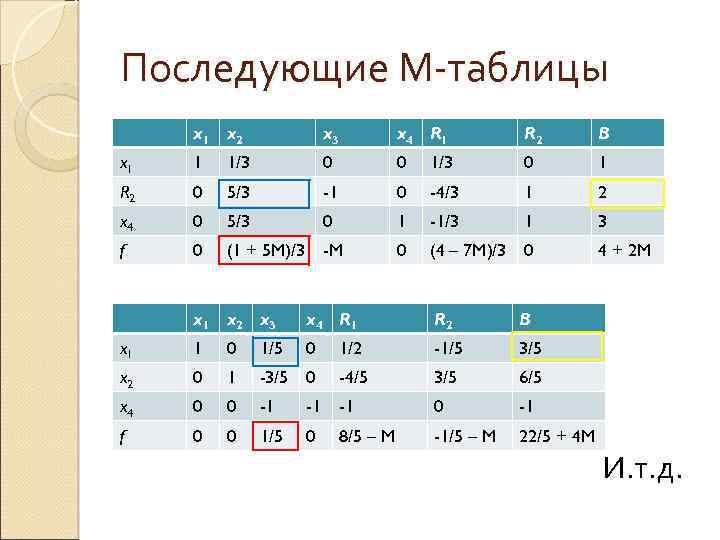Последующие М-таблицы x 1 x 2 x 3 x 4 R 1 R 2 B x 1 1 1/3 0 0 1/3 0 1 R 2 0 5/3 -1 0 -4/3 1 2 x 4 0 5/3 0 1 -1/3 1 3 f 0 (1 + 5 M)/3 -M 0 (4 – 7 M)/3 0 4 + 2 M x 1 x 2 x 3 x 4 R 1 R 2 B x 1 1 0 1/5 0 1/2 -1/5 3/5 x 2 0 1 -3/5 0 -4/5 3/5 6/5 x 4 0 0 -1 -1 -1 0 -1 f 0 0 1/5 0 8/5 – M -1/5 – M 22/5 + 4 M И. т. д.

Двухэтапный метод Это модифицированный М-метод Поиск начального допустимого базисного решения 2. Решение исходной задачи Первый этап минимизирует сумму искусственных переменных при исходных ограничениях Если минимальное значение этой новой целевой функции больше нуля, то исходная задача не имеет допустимого решения. 1.

Пример x 1 x 2 x 3 x 4 R 1 R 2 B R 1 3 1 0 0 1 0 3 R 2 4 3 -1 0 0 1 6 x 4 1 2 0 1 0 0 4 r 0 0 -1 -1 0

Преобразуем r-строку x 1 x 2 x 3 x 4 R 1 R 2 B R 1 3 1 0 0 1 0 3 R 2 4 3 -1 0 0 1 6 x 4 1 2 0 1 0 0 4 r 7 4 -1 0 0 0 9 x 1 x 2 x 3 x 4 R 1 R 2 B x 1 1 1/3 0 0 1/3 0 1 R 2 0 5/3 -1 0 -4/3 1 2 x 4 0 5/3 0 1 -1/3 0 3 r 0 5/3 -1 0 -7/3 0 2

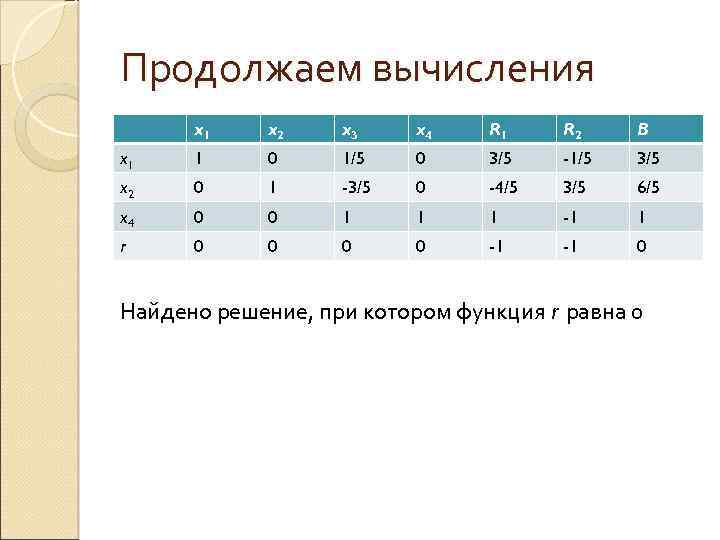Продолжаем вычисления x 1 x 2 x 3 x 4 R 1 R 2 B x 1 1 0 1/5 0 3/5 -1/5 3/5 x 2 0 1 -3/5 0 -4/5 3/5 6/5 x 4 0 0 1 1 1 -1 1 r 0 0 -1 -1 0 Найдено решение, при котором функция r равна 0