М М Корнієнко Історія обчислювальної техніки 1

Зарегистрируйтесь, чтобы просмотреть полный документ!

М. М. Корнієнко Історія обчислювальної техніки (№ 1) Історія лічби та рахунку Способи запису чисел Методи обчислень Харків - 2004

"Кращий метод для передбачення майбутнього розвитку математичних наук полягає у вивченні історії та нинішнього стану цих наук. " Анрі Пуанкаре

Історія обчислювальної техніки (Вступ) 4 "Історія – процес розвитку в природі та суспільстві, хід розвитку чого-небудь; 4 Історія - наука про розвиток якої-небудь галузі знань; 4 Історія - минуле, що зберігається в пам'яті людства. ” (переклад з російської, С. И. Ожегов "Словарь русского языка")

Історія обчислювальної техніки (Вступ) Історію обчислювальної техніки можна умовно поділити на декілька періодів: 1. 2. 3. 4. 5. Використання для лічби та рахунку підручних засобів. Системи нумерації та методи обчислень. Використання пристосувань для рахунку. Створення механічних обчислювальних машин. Створення електронних обчислювальних машин. Останній період в свою чергу поділяється на декілька півперіодів в залежності від поколінь ЕОМ. Останні роки, що характеризуються бурхливим розвитком обчислювальної техніки, вже важко піддаються суворій класифікації, але через деякий час визначиться місце й сьогоднішньому дню в історії обчислювальної техніки.

Історія лічби та рахунку ”Лічити, рахувати - називати в послідовному порядку числа; - визначати суму, кількість чого-небудь. ” (“Короткий тлумачний словник української мови”)

Історія лічби та рахунку Первісні люди не знали чисел і використовували наочне подання інформації для запам'ятовування певної кількості предметів. Для цього використовувалися різні підручні засоби: ракушки, камінчики, інші. Наприклад, щоб запам'ятати те, що на полюванні було вбито п'ять оленів, всіх їх малювали на стіні печери. Поступово люди навчилися рахувати, передаючи свій досвід і знання із покоління в покоління. Самим важким виявилося відділити поняття одиниці від поняття багато. . На первісному етапі розвитку рахунка людина зв'язувала поняття два з поняттям обох рук, у кожній з який знаходиться по одному предмету, а поняття три характеризувалося поняттям обох рук і вказівкою на ногу, де містився третій предмет. Звідси порівняно легко відбулося і виділення поняття чотири, тому що, з одного боку, до цього привело зіставлення двох рук і двох ніг, а з іншого боку можливість помістити по одному предметі в кожної нозі. У багатьох народів рахували за допомогою пальців рук, ніг та інших частин тіла. Наприклад, для рахунку вживалися також лікті, зап`ястки, плечі.

Історія лічби та рахунку Розвиток рахунку пішов значно швидше, коли людина здогадалась звернутися до самого природного рахункового апарата — своїм пальцям. Застосування пальців у рахунку допомогло людині переступити за число, чотири, тому що всі пальці на одній руці можна розглядати як рівноцінні одиниці. Це відразу дозволило довести рахунок до п'яти. Подальший розвиток рахунку зажадав ускладнення рахункового апарату, і людина знайшла вихід, застосовуючи спочатку пальці другої руки, а потім поширюючи цей прийом на пальці ніг: для людей, що не носила взуття, використання пальців ніг був цілком природним. Про це свідчать слова знаменитого російського мандрівника М. М. Миклухо. Маклая, що спостерігав рахунок тубільців Нової Гвінеї: “. . . папуас загинає один за іншим пальці руки, причому видає визначений звук, априклад “бе, бе”. . . Дорахувавши до п'яти, він говорить “ібон-бі” (рука). Потім він загинає пальці іншої руки, знову повторює “бе, бе”. . . , поки не дійде до “ібон-алі” (дві руки). Потім він йде далі, присуджуючи “бе, бе”. . . , поки не дійде до “самба-бі” і “самб-алі” (одна нога, дві ноги). Якщо потрібно лічити далі, папуас користується пальцями рук і ніг когось іншого”.

Історія лічби та рахунку Від пальцевого рахунку бере початок п'ятіркова система числення (одна рука), десяткова (дві руки), двадцяткова (пальці рук і ніг). У багатьох народів пальці рук залишалися інструментом рахунка і на більш високих ступінях розвитку. Також для запам'ятовування кількості предметів використовували зарубки. Цей спосіб рахунку був відомий ще тисячі років тому. Деякі народи вигадали навіть спосіб відшкодування боргів за допомогою зарубок, щось на зразок наших квитанцій. . . На дощечці зарубками відмічався борг, потім дощечка розламувалася навпіл упоперек всіх зарубок. Одна половина віддавалася боржнику, друга - господареві. Такі дощечки називалися "бірки". Коли підходив час віддавати борг, обидві дощечки сполучалися - і відбувався розрахунок. Ніхто не міг підробити зарубки на своїй половині дощечки, оскільки при з`єднанні дощечок зарубки б не співпали. В Англії, наприклад, такий спосіб запису податків існував до кінця XVII ст.

Історія лічби та рахунку Письмо і рахунок вузликами були поширені в індіанців, що населяли територію теперішніх Перу та Чілі. Перуанські рахункові мотузки називалися кіпу (квіпу). Рахували на них за допомогою вузликів. А щоб не забути, що де рахували, кіпу фарбували в різні кольори. Подібний спосіб рахунку застосовували також стародавні індійці та китайці. Нещодавно дослідники виявили, що “кіпу” вузликове письмо, що вживалося інками для утримання в пам'яті великих повідомлень і бухгалтерії, можливо, містить в собі розвинену приховану писемність на основі семибітного двійкового коду. Кіпу стародавніх інків

Історія лічби та рахунку Питання та завдання. 1. Які частини тіла використовувала людина для лічби та рахунку? 2. Які підручні засоби використовувалися для лічби та рахунку? 3. Що таке кіпу? 4. Ким і для чого використовувалися кіпу? 5. Як позначалися на кіпу числа? 6. Як називалися дерев'яні дощечки із зарубками, які призначалися для взаєморозрахунків? 7. Наведіть приклади літературних творів, в яких описується стародавні лічба або рахунок. 8. Складіть мінікросворд. 1. Рахункова мотузка 2. Дощечка або паличка із зарубками 3. Позначення числа на рахунковій мотузці

Способи запису чисел "Число - поняття кількості; - величина, за допомогою якої ведуть рахунок" (“Короткий тлумачний словник української мови”)

Способи запису чисел. Невідомо, коли виникло поняття числа та кількості. Можливо, люди помітили, що при підрахунку різних предметів вони отримували однакову кількість предметів незалежно від того, які предмети підраховувалися. Відділення поняття кількості від поняття предмета привело до виникнення поняття числа. Треба було якось називати й записувати числа, тобто з`явилася необхідність в системі запису чисел або в системі нумерації. Уявлення про поняття числа, що складається у математиків певної епохи, завжди свідчить про той теоретичний і практичний рівень, якого досягла до цього часу математика.

Способи запису чисел. Перші розвинені системи нумерації з`явилися в Древньому Єгипті та Месопотамії (єгипетська та вавілонська цивілізації). Внаслідок археологічних експедицій в Месопотамію, початих в ХIХ ст. , було виявлено декілька сотень глиняних дощечок з нанесеними тонкою паличкою клиновидними написами. . Біля трьохсот з них відносяться до математики. Збереглись і математичні папіруси, що дозволяють дізнатися про арифметику стародавніх єгиптян часів розквіту Верхнього та Нижнього Єгиптів.

Способи запису чисел. Стародавній Єгипет Стародавні єгиптяни для позначення вузлових чисел вигадали спеціальні знаки, які утворилися з ієрогліфів внаслідок їх спрощення для написання рукою. Числа набиралися цими знаками. Порядок розташування символів не мав значення, їх записували або горизонтально, або вертикально. Це була непозиційна система числення. Щоб прочитати число, треба було скласти значення всіх символів, що входять в запис. Для зручності читання символи записувалися по зменшенню або по збільшенню їх значень.

Способи запису чисел. Стародавній Єгипет Спробуйте записати числа в єгипетській нумерації: 4 - _______ 823 - _____________ 974 - _______ 23 - _______ 1998 - _______ 103 - _______ 20000 - _______ 395 - _______ 100101 - _______ Ми бачимо, що в єгипетській системі нумерації запис чисел був дуже громіздким. Недоліком цієї системи було й те, що для великих чисел треба було вигадувати нові ієрогліфи. Саме велике число, для якого зустрічається ієрогліф, було десять мільйонів. Не дивлячись на громіздкий запис чисел, єгиптяни були знайомі з дробами, чисельник яких дорівнювався одиниці.

Способи запису чисел. Вавілон Стародавні вавілоняни використовували для запису чисел два символи: V вертикальний клин ‹ горизонтальний клин До числа 60 принцип запису чисел співпадає з єгипетським (‹ - 10, V - 1) Наприклад, 4 - VVVV 23 - ‹‹ VVV 9 - VVVVV 33 - ‹‹‹ VVV 11 - ‹V 45 - ‹‹‹‹ VVVVV 20 - ‹‹ 59 - ‹‹‹‹‹ VVVVV Ми вже знаємо, що число 10 - "один десяток" - мало своє позначення ( ‹ ). Число 60 позначало "один шестидесяток" і записувалося так само, як 1 (V). Таким чином, в залежності від положення знаку в записі числа ці символи могли позначати різну кількість.

Способи запису чисел. Вавілон Таблиця розвитку клинописних знаків

Способи запису чисел. Вавілон Для того, щоб записати число у вавілонській системі, треба спочатку з'ясувати, скільки разів в ньому укладається число 60, а потім скільки разів в залишку укладається число 10. Якщо кількість разів, що повторюється 60 в заданому числі більше 10, то отримане число треба перетворити тим же способом. Наприклад: Розглянемо шестидесяткову систему числення на життєвих прикладах. Нехай нам відомо, що пішоходи зустрінуться через 71 хвилину. Ми без особливих зусиль обчислюємо, що до їх зустрічі залишилась 1 год. 11 хв. Як ми це порахували? Розглянемо число 71. Поділимо 71 на 60. Отримаємо 1 і 11 в залишку. Поділимо 11 на 10. Отримаємо 1 і 1 в залишку. 18 Таким чином, можна записати: 71 = 60 + 10 + 1 Ми з'ясували, що в число 71 укладається один шестидесяток, один десяток і одна одиниця. 60 ми визначили як 1 година, а 11 хвилин записали в звичній нам десятковій системі числення. 71 мін = 1 ч. 11 мін Запишемо це у вавілонській системі нумерації: V ‹V У даному прикладі ми використали шестидесяткову та десяткову системи числення.

Способи запису чисел. Вавілон У цих прикладах ми бачимо, що величина числа залежить не тільки від набору символів, але і від порядку їх розташування. Це позиційна система числення. У вавілонській системі числа 1, 60, 3600, . . . , а іноді і дроби 1/60, 1/3600, . . . позначалися одним вертикальним клином: V. І тільки з умови задачі можна визначити, про яке число йде мова. Пізніше для позначення пропущеного розряду став використовуватися подвійний клин, але він не ставився в кінці чисел. Також у вавілонських записах застосовується знак пропущеного розряду дві перехрещені стрілки. Але цей нуль ще не був цифрою, а був тільки позначенням пропущеного розряду. Це був, мабуть, перший нуль в історії людства, який використовували вавілонські астрономи та математики ще 300 р. до н. е. Але не дивлячись на ці складності у вавілонській системі, як і в будь-якій позиційній системі числення, не треба було вводити нові символи для запису великих чисел. Також перевага позиційного принципу вавілонян (в порівнянні, наприклад, з системою єгиптян) виявляється і при запису дробів.

Способи запису чисел. Американські індійці На початку нашої ери індійці племені майя, що проживали в Центральній Америці, використовували для запису чисел двадцятирічну позиційну систему числення. Числа записувались з використанням принципу додавання (як у вавілонян). Одиницю позначали крапкою, п’ять - горизонтальною рискою. Наприклад: 1 - • 5 - — 2 - • • 4 - : : Незалежно від вавілонян нуль виник і в племені майя , але тільки як позначення пропущеного розряду. Нуль нагадував напівзакрите око.

Способи запису чисел. Стародавня Греція Особлива роль в розвитку західної цивілізації належить Греції. У Греції в VI ст. до н. е. відбувається розквіт наук. Знаходячись в постійному контакті з народами Сходу, Вавилону, Єгипту греки не задовольнялися лише засвоєнням їх знань, вони створили свою власну математику. Багато разів протягом шкільних років Ви зустрінетесь з іменами Фалеса, Піфагора, Гіппократа, Сократа, Платона, Евкліда, Архімеда, Герона та інших стародавніх грецький вчених, що зіграли важливу роль в розвитку світової науки і культури. Протягом тисячоліття Греція залишалася "колискою наук".

Способи запису чисел. Стародавня Греція У Греції в V ст. до н. е. була поширена аттична система числення, особливу роль в якій грало число 10. Вона містила в собі символи для позначення наступних шести величин: І - (можливо, просто штрих) - 1, Н - “hekaton” - 100, Γ - “penta ” - 5, Χ - “chilioi” - 1000, Δ - “deka” - 10, Μ - “myrioi” - 10000. Іноді вважають, що для запису чисел 1 - I, 2 - II, 3 - III, 4 - IIII використовувалися самостійні символи, і дана система числення містить 9 вузлових символів. Всі інші числа позначалися комбінаціями цих символів. Запишемо деякі числа в аттичній (поширеної в Аттиці) системі числення: 4 = ΙΙΙΙ 6 = ΓΙ 11 = Δ Ι 1005 = Χ Γ 5 = Γ 15 = Δ Γ В аттичній системі для запису чисел використовується поняття п'ятиразового повторення базового символу (множення на 5 чисел від 10 до 10 000). І записувалося це так: Приклад: 50 = ΓΔ 2615 = Χ ΧΓΗ НΔ Γ 5000 = ΓΧ

Способи запису чисел. Стародавня Греція Поступово в III ст. до н. е. аттична система числення була замінена іонічною (іонійці - одне з основних стародавніх грецьких племен). У ній для запису чисел використовувалися 24 букви грецької абетки (алфавіту) та три додаткових знаки (3 букви семітських народів). Однією буквою кодувалися числа 1 (α), 2 (β), 3 (γ), . . . , 9 (θ), 10 (ι), 20 (κ), . . . , 100 (ρ), 200 (σ), . . . , 900. Щоб відрізнити числа від слів, греки ставили над відповідними буквами горизонтальну межу. ____ Наприклад, γα = 31, δηγ = 473 Для чисел 1000, 2000, . . . , 9000 використовувалися перші 9 букв алфавіту, але зі штрихом зліва: ΄ α, ΄ β, ΄ γ, ΄ δ, ΄ ε, ΄ ζ , ΄η, ΄θ, ΄ι Для інших порядків використовувалися свої символи. Ця система насилу дозволяла запис дробів, доки Діофант (на початку н. е. ) не вигадав вміщувати чисельник і знаменник на різних рівнях. Системи, що використовують для запису чисел букви, називаються алфавітними.

Способи запису чисел. Стародавня Русь Багато народів використовували для запису чисел букви. Алфавітні системи запису чисел використовувалися у стародавніх євреїв, грузин, вірмен, слов'ян. Стародавні слов'яни запозичили принцип запису чисел у греків. Однією буквою кодувалися числа 1, 2, . . . 9, 10, 20, . . . , 90, 100, 200, . . . , 900 так само, як в іонічній системі греків. Над буквами, що використовувалися для кодування чисел, ставили спеціальний знак - титло: ~. Ось так виглядала таблиця вузлових чисел в слов'янській системі нумерації.

Способи запису чисел. Стародавня Русь Для позначення подальших чисел до букв додавалися спеціальні позначки. Наприклад, числа 1000, 2000 і т. д. записувались тими же буквами, що і 1, 2. . . , але зліва внизу ставили спеціальний знак. Число 10 000 називалося на Русі "тьма". До наших днів дійшов вираз "тьма тямуща” , що означає дуже велику кількість будь-чого. В одному із стародавніх рукописів є інша система побудови великих чисел. Великі числа будуються із принципу “стільки разі по стільки”. В тому рукописі “тьма” - це 10 6 - “тисяча разі по тисячі”, “легіон” - 1012 - “тьма темен”, і т. д. Рахунок переривався на “колоді” (на ній “спотикались”), бо “…более сего несть человеческому уму разумевати”. Таким чином слов’яни застосували оригінальний спосіб позначення великий чисел без введення нових цифрових знаків.

Способи запису чисел. Стародавня Русь Користувалися на Русі й дробами, які виходили послідовним розподілом навпіл половини або третьої частини чого-небудь: 1/2 - пів 1/3 - третина 1/6 - півтреті 1/12 - пів-півтрети 1/4 - четь 1/8 - півчеті 1/16 - пів-півчеті 1/24 - пів-півтреті 1/32 - пів-півчеті Стародавні слов'яни також займались і геометрією, їм були відомі деякі властивості кола. Таким чином, ми бачимо, що математичні знання стародавніх слов'ян біля 1000 року н. е. були не нижчими, ніж у західних народів. Але свій подальший розвиток математика на Русі продовжувала вже після падіння татаромонгольського іга. В Росії ще у XVII ст. використовувалась алфавітна цифрова система, що була позичена у Візантії. Новий громадянський шрифт, який зберігся в значній мірі до наших днів, та арабську цифрову символіку ввів Петро Перший у 1708 -1710 рр.

Способи запису чисел. Стародавній Рим Досі ми використовуємо римську систему нумерації, в якій сім чисел позначаються буквами: 1 - I, 5 - V, 10 - X, 50 - L, 100 - C, 500 - D, 1000 - M, а інші числа записуються комбінаціями цих букв. Деякі принципи запису чисел у римській системі спільні з аттичною системою. Але є й нові ідеї, пов'язані з порядком розташування символів. Якщо в запису числа букви розташовані в порядку зменшення їх числових значень, то відповідні ним числа додаються, наприклад, VI = 5 + 1 = 6 XVII = 10 + 5 + 1 = 17 MDX = 1000 + 500 + 10 = 1510, а якщо - збільшення - віднімаються, наприклад, IV = 5 - 1 = 4 XIV = 10 + 5 - 1 = 14 MXD = 1000 + 500 - 10 = 1490.

Способи запису чисел. Стародавня Індія “Лише у індійців вперше в історії людства з'явився нуль як математичний символ, який використовувався в рахункових операціях. Він з'явився не пізніше 458 р. н. е. ” (історик Еберхард Кноблох). Чому ж індійці почали використовувати нуль в своїх обчисленнях? Мабуть тому, що “в Індії, на відміну від Греції, ніколи не відчували жаху перед нескінченністю та пустотою - навпаки перед цими поняттями схилялися. ” (історик Ч. Сейф). Спочатку індійці використовували слова для позначення чисел. Наприклад, нуль “порожній”, “небо”, “діра”; двійка - “близнюки”, “очі”, “крила”. Так у записах ІІІ-ІV ст. н. е. число 1021 записано як “місяць - діра - крила - місяць”. Лише в V ст. великий математик Арьябхата почав використовувати для запису чисел букви санскритського алфавіту. Потім замість букв почали використовувати особисті позначки - цифри. Ця скорочена форма запису виявила всі переваги десяткової системи числення.

Способи запису чисел. Стародавня арабська цивілізація У VII-VIII ст. кочові племена Аравії завоювали великі території. В 711 р. араби підкорили Іспанію, в 712 р. - частину Індії. Утворилася величезна мусульманська імперія. В мусульманських містах почала розвиватися наука. Звичні нам арабські цифри запозичені арабами у стародавніх індійців. Індійську десяткову позиційну систему числення з нулем популяризував в своїх трактатах відомий арабський математик аль Хорезмі (IX ст. ). Поступово протягом ХI і ХII століть новий спосіб рахунку почав розповсюджуватись на Заході. І звичні нам цифри отримали назву "арабських". Аль Хорезмі В деяких сучасних арабських країнах, таких як Іран, Пакистан, Афганістан, залишилась стара арабська система числення, яка суттєво відрізняється від системи, що була запозичена арабами в Індії.

Способи запису чисел. Порівняйте способи запису чисел у різних народів.

Способи запису чисел. Питання та завдання 1. Як з` явилося поняття числа? 2. Як ще можна назвати систему запису чисел? 3. Запишіть в більш зручній формі наступні величини: 100 хв. , 10 000 сек. , 1200 сек. , 661 хв. Які системи числення Ви при цьому використали? 4. Як стало відомо про вавілонську арифметику? 5. Який знак використовувався в стародавніх вавілонян для позначення: розрядної одиниці , десяти одиниць, пропущеного розряду ? 6. Запишіть у вавілонській нумерації наступні числа: 4 , 78 , 12 , 133, 53 , 3600 7. Які числа грали важливу роль у вавілонській нумерації? 8. Як стало відомо про єгипетську арифметику? 9. Наведіть приклади символів, що використовувались у єгипетській системі запису чисел. 10. Ступені якого числа грали важливу роль в єгипетській нумерації?

Способи запису чисел. Питання та завдання 11. Як називалися системи запису чисел, що застосовувались стародавніми греками? 12. Які символи застосовувались в аттичній системі? 13. Запишіть в аттичній системі наступні числа: 2 - _____ 14 - ______ 122 - _________ 4 - _____ 26 - ______ 444 - _________ 6 - _____ 41 - ______ 505 - _________ 8 - _____ 55 - ______ 618 - _________ 10 - _____ 83 - ______ 2522 - _________ 14. Які символи застосовувались в іонічній системі? 15. Як греки уникали плутанини між записом слів і чисел в іонічній системі? 16. Як називається система запису чисел за допомогою букв? 17. Які народи використовували таку систему запису чисел?

Способи запису чисел. Питання та завдання 18. Яка система запису чисел існувала в Стародавній Русі? 19. Як в Стародавній Русі називався знак, що використовувався над буквами для позначення чисел? 20. Запишіть в слов'янській нумерації наступні числа: 4 - ______ 444 - _________ 12 - ______ 21 - ______ 122 - _________ 21. Що позначають вузлові числа римської нумерації? I - _____ V - _____ X - _____ С - _____ D - _____ L - _____ M - _____ 22. Запишіть римські числа від 1 до 10. 23. Запишіть римські символи для позначення чисел в порядку зменшення їх значень? 24. Запишіть римськими цифрами приведені нижче числа. 4 - _______ 6 - _______ 40 - _______ 60 - _______ 400 - _______ 600 - _______ 900 - _______ 1100 - _______

Способи запису чисел. Питання та завдання. 25. Продовжить рядок чисел. 3, 5, 7, 9, . . . , . II, IV, VIII, . . . , . 1, 2, 3, 5, 8, 13, . . . , . V, X, XV, XX, . . . , . 1, 4, 9, 16, . . . , . X, XXX, . . . , . . 26. Запишіть пропущені числа. 7, . . . , 21, 28, 35, . . . , 56, 63, . . . , 77, 84, . . I , . . . , III, . . . , VII , . . . , IX , . . . , XIII. 27. Обчисліть значення римських чисел. LXXVI = DXXXV = MXMXVII = LVIII = DXI = СІІ =

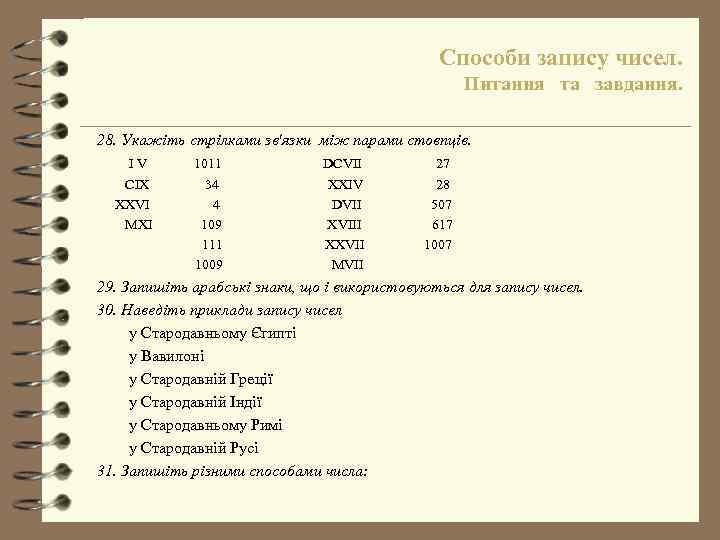
Способи запису чисел. Питання та завдання. 28. Укажіть стрілками зв'язки між парами стовпців. IV CIX XXVI MXI 1011 34 4 109 111 1009 DCVII XXIV DVII XVIII XXVII MVII 27 28 507 617 1007 29. Запишіть арабські знаки, що і використовуються для запису чисел. 30. Наведіть приклади запису чисел у Стародавньому Єгипті у Вавилоні у Стародавній Греції у Стародавній Індії у Стародавньому Римі у Стародавній Русі 31. Запишіть різними способами числа:

Способи запису чисел. Питання та завдання. Складіть кросворди: 32. Кросворд "Слов'янська система-1". По вертикалі: Система, в якій для запису чисел використовуються букви. По горизонталі: Назви старослов`янських букв, які використовувались для написання тих чисел, значення яких записані праворуч:

Способи запису чисел. Питання та завдання. 33. Кросворд "Слов'янська система-2". По вертикалі: Система, яка використовувалась для запису чисел в Стародавній Русі. По горизонталі: Назви старослов`янських букв, які використовувались для написання чисел, значення яких записані праворуч:

Способи запису чисел. Питання та завдання. 34. Кросворд "Системи рахунку - 1". Система рахунку 1. у Стародавній Русі 2. у Месопотамії -ська 3. у Стародавній Греції 4. на берегах Нілу 35. Кросворд "Системи рахунку - 2". Система рахунку, в якій 1. у Стародавній Греції для запису чисел використовувались букви; 2. для запису чисел використовуються букви; 3. внесок в число дає не тільки символ, але й місце його розташування; 4. у Стародавній Греції для запису чисел використовувались вузлові символи; -на

Способи запису чисел. Питання та завдання. 36. Кросворд "Історія рахунку" По горизонталі: 1. Матеріал, на якому писали стародавні єгиптяни. 2. Символ для запису чисел у вавілонян. 3. Символ для запису чисел у єгиптян. 4. Матеріал, на якому писали стародавні вавілоняни. 5. Символ для запису чисел у слов'ян. 6. Певне місце для символу в деяких системах числення. 7. Спеціальний знак для позначення чисел у слов'ян. По вертикалі: Система знаків для запису слів і чисел.

Способи запису чисел. Питання та завдання. 37. Складіть кросворд, використовуючи деякі наведені поняття. · · · · Дощечка або паличка із зарубками Рахункова мотузка Позначення числа на рахунковій мотузці Частина тіла, що використовувалась при рахунку 10 000 в слов'янській системі числення Система символів для запису слів і чисел Символ для позначення чисел в слов'янській системі 400 в слов'янській системі числення 20 в слов'янській системі числення 70 в слов'янській системі числення Ріка в країні, де для запису чисел використовувались ієрогліфи 30 в слов'янській системі числення Символ для запису чисел в єгипетській системі 9 в слов'янській системі числення Символ для запису чисел в вавілонській системі 50 в слов'янській системі числення

Методи обчислень “Обчислити - встановити, підраховуючи” (“Короткий тлумачний словник української мови”)

Методи обчислень Ми познайомилися з різними записами чисел. Не у всіх системах нумерації над числами відбувалися арифметичні дії звичним для нас способом. Додавати та віднімати числа в різних системах запису було не дуже складно. Розглянемо ці арифметичні дії на прикладі римської системи. 1. XI + IV = X + I - I + V = XV XI + IV = (10 + 1) + (5 - 1) = 15 2. XI - IV = X + I - V = (X - V) + (I + I) = V + I = VII XI - IV = (10 + 1) - (5 - 1) = 7 3. MXС + LI = M - X + З + L + I = M + З + L - X + I = MCXLI MXС + LI = 1000 + (100 - 10) + 50 + 1 = 1141 Аналогічно можна проводити складання і віднімання і в інших системах запису чисел.

Методи обчислень Множення та ділення вже являють собою серйозну проблему. У вавілонській системі запису чисел таблиця множення була такою великою (до 59 х 59), що при обчисленнях треба було мати цю таблицю при собі, тому що запам'ятати її було дуже складно. Стародавні єгиптяни також вміли ділити та множити. Робили вони це дуже оригінальним способом. Спробуємо в ньому розібратися. Особливу роль у єгиптян при множенні та діленні грало число два та його ступені: 4, 8, 16, 32 і т. д. Множення та ділення проводилося шляхом послідовного подвоєння чисел. Розглянемо детальніше спосіб множення єгиптян.

Методи обчислень 1. Спробуємо єгипетським методом помножити 5 на 17 (числа будемо записувати в сучасній символіці, суть методу від цього не зміниться). У лівій колонці будемо записувати ступені двійки - те, на що буде множитися число 17. У правій колонці - результат чергового подвоєння. 1 ¦ 2 4 17 34 ¦ 68 Цей процес подвоєння будемо проводити доти, поки з елементів правого стовпця можна буде скласти потрібний множник (в нашому випадку, 5 = 1 + 4). Відмітимо знаком ” ¦ “ ті рядки, де зліва були розташовані числа, з яких складається множник ” 5 “. Щоб отримати множення 5 на 17, складемо праві частини помічених рядків: 17 + 68 = 85. Дійсно, 5 * 17 = (1+4) * 17=17 + 4 * 17=17 + 68 = 85 Відповідь: 5 * 17 = 85

Методи обчислень 2. Розглянемо ще один приклад. Знайдемо множення 13 на 57. 1 ¦ 57 2 114 4 ¦ 228 8 ¦ 456 13 = 1 + 4 + 8 13 * 57 = 57 + 228 + 456 = 741 Відповідь: 13 * 57 = 741 Таким же чином єгиптяни проводили й ділення.

Методи обчислень Греки мали в своєму розпорядженні таблицю множення до 9 х 9 і проводили множення, враховуючи основне число і його порядок. Наприклад, , помножимо 30 на 200. Число 30 має основне число , яке дорівнюється 3, і порядок - 10 (30 = 3 * 10) Число 200 має основне число , яке дорівнюється 2, і порядок - 100 (200 = 2 * 100) Добуток основних чисел: 3 * 2 = 6. Добуток порядків: 10 * 100 = 1000. Отже, результат дорівнюється 6 000. Складність цієї процедури була величезною, коли перемножувались ні такі прості числа.

Методи обчислень Питання та завдання 1. У римській системі нумерації складіть числа: а) XXI та VI б) XXXVI та XIX в) LXXIV та CXVI г) DXLIII та LXXV д) MCMXCVIII та II 2. У римській системі нумерації знайдіть різницю чисел: а) б) в) г) д) XXI та VI XXXVI та XXI LXV та CX СDIII та LXIX CMXCIX та III

Методи обчислень. Питання та завдання 3. Використовуючи єгипетський метод подвоєнь знайдіть добутки: а) 7 на 11 1 2 4 11 22 44 б) 17 на 20 1 2 4 8 16 20 40 80 160 320 в) г) д) е) 17 на 11 13 на 80 20 на 6 37 на 50

Іменний покажчик Бібліографічні дані про людей, чиї імена зустрічались у тексті презентації

Іменний покажчик Ал-Хорезмі Абу Абдалах (або Абу Джафар) Мухамед ібн Муса (народ. до 800 р. , помер після 847 р. ). Жив у Багдаді. Основні роботи по теорії квадратних рівнянь, теорії десяткової системи. Архимед (ок. 287 -212 до н. е. ) - древньогрецький вчений, родом з Сіракуз. Автор багатьох винаходів. Розробив методи знаходження площин поверхні та об'єму різних фігур та тіл. Організатор технічної оборони Сіракуз від римлян. Герон (Олександрійський) (рр народж. та смерті невідомі, приблизно 1 ст. ) древньогрецький вчений. Надав систематичне викладення основних досягнень античного світу з прикладної математики та механіки. Винахідник приборів та автоматів. Діофант - древньогрецький математик. Евклід ( 3 ст. до н. е. ) - древньогрецький математик, працював в Олександрії. Головна праця - “Початки” (15 книг), що включає основи античної математики, теорії чисел, загальної теорії відносин та метода знаходження площин та об'ємів. , Миклухо-Маклай Миколайович (1846 -1888) - російський етнограф, вивчав населення Південно-Східної Азії, Австралії, Океанії, також папуасів Нової Гвінеї (зараз берег Миклухо-Маклая).

Іменний покажчик Ожегов Сергій Іванович (1900 -1964) - радянський мовознавець, лексиколог, дослідник норм літературної російської мови, доктор філологічних наук, професор. Піфагор (ок. 570 - ок. 500 до н. е. ) - древньогрецький філософ, політичний діяч, математик. Створив вчення про подобу, доказав теорему про співвідношення боків трикутника, вчення пропорції. Платон (428 - 348 до н. е. ) - древньогрецький філософ, учень Сократа. Пуанкаре (Poincare) Жюль Анрі (1854 -1912) - французький математик, фізик та філософ, член - кореспондент Петербурзької Академії Наук. Сократ (ок. 470 - 399 до н. е. ) - древньогрецький філософ. Вважав, що мета філософії - самопізнання як шлях до досягнення істинного блага. Був звинувачений в “поклонении новым божествам” і приговорений до страти, прийняв отруту. Для послідуючих поколінь став ідеалом мудреця. Фалес (640 - 562 чи 550 до н. е. ) - древньогрецький філософ, засновник мілетської школи, перший із “семи мудреців”.

Післямова Презентація “Історія обчислювальної техніки” (CSH-1. 3 - Computer System History - версія 1. 3) складається з чотирьох частин і є комп'ютерною підтримкою авторської програми спецкурсу ”Історія обчислювальної техніки в прикладах та задачах” для учнів 5 -7 класів вчителя інформатики М. М. Корнієнко. Презентація № 1 - “Історія лічби та рахунку”. “Способи запису чисел”. “Методи обчислень”. Презентація № 2 - “Системи числення”. Презентація № 3 - “Прилади для лічби”. “Механічні обчислювальні машини”. Презентація № 4 - “Електронно-обчислювальні машини”. Методичний матеріал до програми спецкурсу: · · · Календарно-тематичне планування. Зошит учня. Комп’ютерні презентації № 1 -4. Розробка підсумкового уроку (турнір). Список літератури та сайтів за темою. Авторська програма спецкурсу призначена для учнів 5 -7 класів. Також вона може бути використана і на факультативних заняттях з інформатики для початківців.

Скачать презентацию М М Корнієнко Історія обчислювальної техніки 1

tetr1_ukr.ppt

Количество слайдов: 52