М Ф Степанов Системное программное обеспечение 5 Формальные

М. Ф. Степанов Системное программное обеспечение 5. Формальные языки и грамматики

5. 1. Основные понятия, используемые в теории формальных языков Алфавит - непустое конечное множество элементов. Символы - элементы алфавита. Цепочка - конечная последовательность символов алфавита. Например, если A = {a, b, c} - алфавит, то a, b, с, ab, aaca -цепочки. В цепочках важен порядок символов ab и ba - разные цепочки. . или e - пустая цепочка. Другие обозначения: x. R цепочка x с символами в обратном порядке xn цепочка x, повторенная n раз x* цепочка x, повторенная 0 или более раз x+ цепочка x, повторенная 1 или более раз 2

5. 1. Основные понятия, используемые в теории формальных языков Длина цепочки равна числу символов в цепочке. Если x - цепочка, то - ее длина. , , . Конкатенация цепочек. Если X и Y цепочки, то их конкатенацией XY является цепочка, полученная путем дописывания символов цепочки Y вслед за символами цепочки X. Если X = ab и Y = сd, то XY = abcd, . Буквы x, y, z, u, v, w, t будем применять для обозначения цепочек. 3

5. 1. Основные понятия, используемые в теории формальных языков Длина цепочки равна числу символов в цепочке. Если x - цепочка, то - ее длина. , , . Конкатенация цепочек. Если X и Y цепочки, то их конкатенацией XY является цепочка, полученная путем дописывания символов цепочки Y вслед за символами цепочки X. Если X = ab и Y = сd, то XY = abcd, . Буквы x, y, z, u, v, w, t будем применять для обозначения цепочек. 4

5. 1. Основные понятия, используемые в теории формальных языков Произведение цепочек. Произведение двух множеств цепочек А и В есть. . Если и , то. Степени цепочек. Если x - цепочка, то ; ; . . . ; для. Степени алфавита. Если А - алфавит, то , . , для. Итерация. Используя понятие степени алфавита определим итерацию множества А: Усеченная итерация. Например, если А = {a, b, c}, то. = {a, b, c, aa, ab, ac, ba, bb, bc, ca, cb, cc, aaa, . . . }; 5. = {, a, b, c, aa, ab, ac, ba, bb, bc, ca, cb, cc, aaa, . . . }.

5. 2. Формальное определение грамматики и языка Правило подстановки (или продукция) упорядоченная пара (U, x), которая записывается так , или , где U - символ; x - конечная цепочка символов; знаки ": : =", ": ", "->" означают фразу "может состоять из". Грамматика G[z] - конечное непустое множество правил подстановки, где z - начальный символ (или аксиома). Этот символ z должен встретиться в левой части по крайней мере одного правила подстановки. 6

5. 2. Формальное определение грамматики и языка Символы, которые встречаются в левых и правых частях правил подстановки, образуют словарь. Символы, которые встречаются в левых частях правил подстановки, называются нетерминальными. Символы, которые не входят в множество нетерминальных символов, называются терминальными. Таким образом, словарь V есть , . где Vt - множество терминальных символов; Vn- множество нетерминальных символов. 7

5. 2. Формальное определение грамматики и языка Как правило, нетерминальные символы заключают в угловые скобки <u>, чтобы отличить их от терминалов. Множество правил с одинаковыми левыми частями сокращенно записывают как Пример. Грамматика целого числа : Такая форма записи грамматики называется нормальной формой Бэкуса-Наура. 8

5. 2. Формальное определение грамматики и языка Основное назначение грамматики порождение синтаксически правильных предложений языка. Рассмотрим порождение цепочек. Цепочка v непосредственно порождает цепочку w (или w непосредственно выводится из v): , если для некоторых цепочек x и y можно записать. и , где - правило грамматики. 9

5. 2. Формальное определение грамматики и языка Цепочка v порождает цепочку w (или w выводима из v): , если существует последовательность непосредственных выводов Обозначим или. , если 10

5. 2. Формальное определение грамматики и языка Цепочка x называется сентенциальной формой, если x выводима из начального символа грамматики G[z], т. е. . Предложением называется сентенциальная форма, состоящая только из терминальных символов. Языком L называется множество предложений, порождаемых грамматикой G[z], т. е. 11

5. 2. Формальное определение грамматики и языка Грамматика рекурсивна по отношению к U, если. Если , то имеет место левая рекурсия. Если , то имеет место правая рекурсия. Правило подстановки называется леворекурсивным, если оно имеет вид U: : =U. . . , праворекурсивным, если оно имеет вид U: : =…U. Рекурсивная грамматика описывает бесконечный язык, то есть порождает бесконечное число предложений. Грамматика целого числа G 1[<число>] описывает бесконечный язык, так как имеет леворекурсивное правило. 12

5. 3. Классификация формальных языков Грамматики типа 0 не накладывают никаких ограничений на правила подстановки. Грамматики типа 1, или контекстно - зависимые, Это означает, что подстановка имеет место только в контексте между x и y. Грамматики типа 2 или контекстно-свободные, содержат в левой части правил подстановки только один нетерминальный символ; его применение не будет зависеть от контекста: Грамматики типа 3 имеют языки, задаваемые посредством регулярных грамматик, допускающих только правила подстановки вида: U: : =t, или U: : =t. N 13

5. 4. Языки и грамматики Множество всех цепочек из элементов множества E естественно обозначить через E*. Язык - это подмножество E*. Примеры языков: Си, русский, { 0 n 1 n | n >= 0 }. Язык можно задать: Ø перечислив все цепочки; Ø написав программу-распознаватель, которая получает на вход цепочку символов и выдает ответ "да", если цепочка принадлежит языку и "нет" в противном случае; Ø с помощью механизма порождения - грамматики. 14

5. 4. Языки и грамматики Чтобы задать грамматику, требуется указать: множество E символов алфавита (или терминальных символов). Будем обозначать их строчными символами алфавита и цифрами; множество нетерминальных символов (или метасимволов), не пересекающееся с E, со специально выделенным начальным символом S. Будем обозначать их прописными буквами; множество правил вывода, определяющих правила подстановки для цепочек. Каждое правило состоит из двух цепочек (например, x и y), причем x должна содержать, по крайней мере, один нетерминал; и означает, что цепочку x в процессе вывода можно заменить на y. Вывод цепочек языка начинается с нетерминала S. 15

5. 4. Языки и грамматики Рассмотрим язык простейших арифметических формул: <формула>: (<формула>)|<число>|<формула><знак><формула> <знак> : + | * Почему "3+5*2" является формулой? Приведем последовательность преобразований цепочек (так называемый "разбор" или "вывод"): <формула> <знак><формула> : <формула><знак><формула> : <число> <знак><формула><знак><формула> : 3 + <число> <знак><формула> : 3 + 5 * <число> : 3 + 5 * 2 16

5. 4. Языки и грамматики Если для одной и той же цепочки можно изобразить два разных дерева разбора (или, что то же самое, построить, два разных правых вывода), грамматика называется неоднозначной. Тот же самый язык можно описать однозначной грамматикой: <формула> : <терм> | <терм><знак><формула> <терм> : (<формула>) | <число> <знак> : + | * 18

5. 5. Языковые процессоры как компиляторы Языковые процессоры подсистем общения САПР САУ осуществляют преобразование информации, вводимой пользователем (постановки задач проектирования, исходные данные для решения задач и т. п. ) из внешней формы представления на языке пользователя во внутреннее представление на языках представления данных и знаний. Перевод с одного языка на другой называется трансляцией или компиляцией. 19

5. 5. Языковые процессоры как компиляторы Так как любую инфиксную формулу можно переписать в постфиксную запись с сохранением порядка следования чисел, то для компиляции формулы из инфиксной в постфиксную запись следует выделить внешнюю операцию, записать в постфиксной форме оба операнда и записать операцию вслед за ними. Для перевода операнда в постфиксную запись можно рекурсивно обратиться к программе перевода формулы. Однако следование правилам грамматики при компиляции формулы за один ее просмотр слева направо приводит к следующему фрагменту: Comp. Form() { Comp. Form(). . . выполнение которого, конечно же, никогда не завершится. Проблема возникла из-за того, что цепочки в левой и правой частях правила начинаются с одного нетерминала (говорят, что грамматика леворекурсивна). 20

5. 5. Языковые процессоры как компиляторы Если устранить левую рекурсию: <формула> : <терм> | <терм><плюс-минус><формула> <терм> : <элемент>|<элемент><умножить-разделить><терм> <плюс минус> : +|<умножить разделить> : * | / то описанная проблема исчезнет, рекурсивный компилятор можно будет написать, однако появятся новые трудности Фактически, преобразовав грамматику, мы изменили порядок свертки операций. Традиционно операции одного приоритета выполняются слева направо (говорят, что операции левоассоциативны), а только что написанная грамматика определяет операции как правоассоциативные. 21

5. 5. Языковые процессоры как компиляторы Наиболее просто решить эту проблему можно, добавив в метаязык НФБН символы итерации {} "повторить 0 или более раз". С применением новых обозначений грамматика легко запишется без левой рекурсии: <формула> : <терм> { <плюс минус> <формула> } <терм> : <элемент> {<умножить разделить> <элемент>} 22

5. 5. Языковые процессоры как компиляторы Использованная при написании компилятора техника носит название рекурсивного спуска. Входную цепочку мы просматриваем слева направо, дерево вывода проходим сверху вниз (т. е. от начального нетерминала <формула>). Если разбор цепочки-программы сопровождается не переводом ее в другое представление для дальнейшего выполнения, а немедленным исполнением (в нашем случае - вычислением значения), говорят, что программа интерпретируется. 23

5. 6. Способы представления грамматики языков Нормальная форма Бэкуса (БНФ) Скобочная форма записи Синтаксические графы 24

5. 7. Построение регулярных грамматик Регулярные грамматики являются наиболее простыми и для них могут быть построены эффективные языковые процессоры. Большинство языков современных САПР или описываются регулярными грамматиками, или могут быть приведены к ним. 25

5. 7. Построение регулярных грамматик 1 этап. Осуществляется анализ предложений языка, заключающийся в определении всех допустимых типов предложений. 2 этап. Записывается грамматика, порождающая данные предложения в скобочной форме. 3 этап. Строится синтаксический граф, используя скобочную форму записи и правила преобразования 4 этап. На основе полученного синтаксического графа записывается грамматика в БНФ. 26

5. 7. Построение регулярных грамматик Рассмотрим методику построения регулярных грамматик на примере грамматики действительных чисел. 1 этап. 12. 75; . 1; 167. ; 3. 14 Е +5; . 72 Е -15; 84. Е 7; 27

5. 7. Построение регулярных грамматик Рассмотрим методику построения регулярных грамматик на примере грамматики действительных чисел. 2 этап. 28

5. 7. Построение регулярных грамматик Рассмотрим методику построения регулярных грамматик на примере грамматики действительных чисел. 3 этап. 29

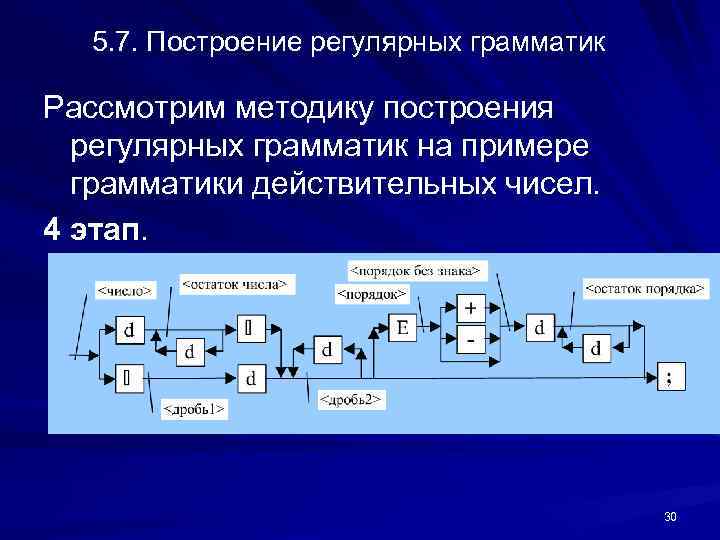
5. 7. Построение регулярных грамматик Рассмотрим методику построения регулярных грамматик на примере грамматики действительных чисел. 4 этап. 30

5. 7. Построение регулярных грамматик Рассмотрим методику построения регулярных грамматик на примере грамматики действительных чисел. 4 этап. <число> : : = d<остаток числа>|. <дробь 1> <остаток числа> : : = d<остаток числа>|. <дробь 2> <дробь 1> : : = d<дробь 2>|E<порядок>|; <порядок> : : = +<порядок без знака>| -<порядок без знака>| d<остаток порядка> <порядок без знака> : : = d<остаток порядка>|; 31