290fa787807015a00f94f0e5dacbb0b3.ppt
- Количество слайдов: 169
 M. A. V. REVISION LECTURES MATHEMATICAL METHODS UNITS 3 AND 4 Presenter: MICHAEL SWANBOROUGH Flinders Christian Community College
M. A. V. REVISION LECTURES MATHEMATICAL METHODS UNITS 3 AND 4 Presenter: MICHAEL SWANBOROUGH Flinders Christian Community College
 Examinations EXAMINATION 1 - Facts, Skills and Applications Task Part A - Multiple-choice questions Part B - Short-answer questions EXAMINATION 2 - Analysis Task
Examinations EXAMINATION 1 - Facts, Skills and Applications Task Part A - Multiple-choice questions Part B - Short-answer questions EXAMINATION 2 - Analysis Task
 Examination Advice General Advice • Answer questions to the required degree of accuracy. • If a question asks for an exact answer then a decimal approximation is not acceptable. • When an exact answer is required, appropriate working must be shown.
Examination Advice General Advice • Answer questions to the required degree of accuracy. • If a question asks for an exact answer then a decimal approximation is not acceptable. • When an exact answer is required, appropriate working must be shown.
 Examination Advice General Advice • When an instruction to use calculus is stated for a question, an appropriate derivative or antiderivative must be shown. • Label graphs carefully – coordinates for intercepts and stationary points; equations for asymptotes. • Pay attention to detail when sketching graphs.
Examination Advice General Advice • When an instruction to use calculus is stated for a question, an appropriate derivative or antiderivative must be shown. • Label graphs carefully – coordinates for intercepts and stationary points; equations for asymptotes. • Pay attention to detail when sketching graphs.
 Examination Advice General Advice • Marks will not be awarded to questions worth more than one mark if appropriate working is not shown.
Examination Advice General Advice • Marks will not be awarded to questions worth more than one mark if appropriate working is not shown.
 Examination Advice Notes Pages • Well-prepared and organised into topic areas. • Prepare two pages of general notes. • Prepare two separate pages for each of the two examinations. • Include process steps rather than just specific examples of questions.
Examination Advice Notes Pages • Well-prepared and organised into topic areas. • Prepare two pages of general notes. • Prepare two separate pages for each of the two examinations. • Include process steps rather than just specific examples of questions.
 Examination Advice Notes Pages • Some worked examples can certainly be of benefit. • Include key steps for using your graphic calculator for specific purposes. • Be sure that you know the syntax to use with your calculator (Ctlg. Help is a useful APP for the TI-83+)
Examination Advice Notes Pages • Some worked examples can certainly be of benefit. • Include key steps for using your graphic calculator for specific purposes. • Be sure that you know the syntax to use with your calculator (Ctlg. Help is a useful APP for the TI-83+)
 Examination Advice Strategy - Examination 1 • Use the reading time to plan an approach for the paper. • Make sure that you answer each question. There is no penalty for incorrect answers. • It may be sensible to obtain the “working marks” in the short answer section before tackling the multiple choice questions.
Examination Advice Strategy - Examination 1 • Use the reading time to plan an approach for the paper. • Make sure that you answer each question. There is no penalty for incorrect answers. • It may be sensible to obtain the “working marks” in the short answer section before tackling the multiple choice questions.
 Examination Advice Strategy - Examination 1 • Some questions require you to work through every multiple-choice option – when this happens don’t panic!! • Eliminate responses that you think are incorrect and focus on the remaining ones. • Questions generally require only one or two steps – however, you should still expect to do some calculations.
Examination Advice Strategy - Examination 1 • Some questions require you to work through every multiple-choice option – when this happens don’t panic!! • Eliminate responses that you think are incorrect and focus on the remaining ones. • Questions generally require only one or two steps – however, you should still expect to do some calculations.
 Examination Advice Strategy - Examination 2 • Use the reading time to carefully plan an approach for the paper. • Momentum can be built early in the exam by completing the questions for which you feel the most confident. • Read each question carefully and look for key words and constraints.
Examination Advice Strategy - Examination 2 • Use the reading time to carefully plan an approach for the paper. • Momentum can be built early in the exam by completing the questions for which you feel the most confident. • Read each question carefully and look for key words and constraints.
 Examination Advice Strategy - Examination 2 • If you find you are spending too much time on a question, leave it and move on to the next. • When a question says to “show” that a certain result is true, you can use this information to progress through to the next stage of the question.
Examination Advice Strategy - Examination 2 • If you find you are spending too much time on a question, leave it and move on to the next. • When a question says to “show” that a certain result is true, you can use this information to progress through to the next stage of the question.
 Revision Quiz 1 2 3 4 5 6 7 8 9
Revision Quiz 1 2 3 4 5 6 7 8 9
 Question 1 The derivative of a) b) d) is equal to c) e) A
Question 1 The derivative of a) b) d) is equal to c) e) A
 Question 2 The range of the function with graph as shown is a) b) c) d) e) B
Question 2 The range of the function with graph as shown is a) b) c) d) e) B
 Question 3 Angie notes that 2 out of 10 peaches on her peach tree are spoilt by birds pecking at them. If she randomly picks 30 peaches the probability that exactly 10 of them are spoilt is equal to a) b) c) d) e) D
Question 3 Angie notes that 2 out of 10 peaches on her peach tree are spoilt by birds pecking at them. If she randomly picks 30 peaches the probability that exactly 10 of them are spoilt is equal to a) b) c) d) e) D
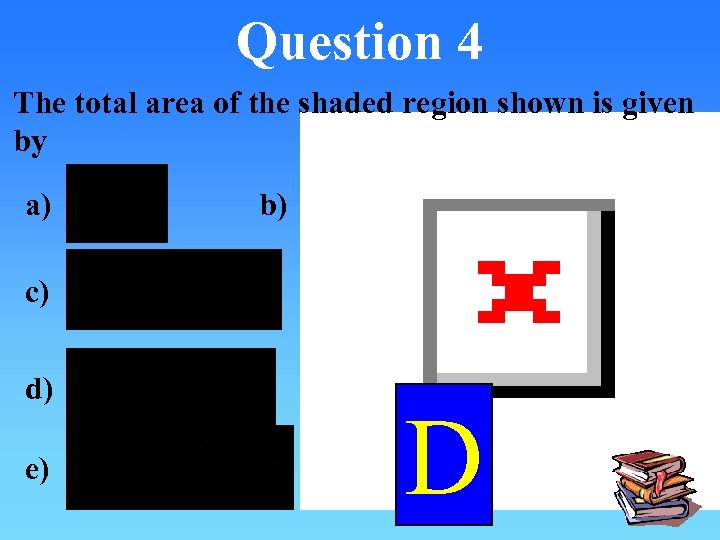 Question 4 The total area of the shaded region shown is given by a) b) c) d) e) D
Question 4 The total area of the shaded region shown is given by a) b) c) d) e) D
 Question 5 What does V. C. A. A. stand for? a) Vice-Chancellors Assessment Authority b) Victorian Curriculum and Assessment Authority c) Victorian Combined Academic Authority d) Victorian Certificate of Academic Aptitude e) None of the above B
Question 5 What does V. C. A. A. stand for? a) Vice-Chancellors Assessment Authority b) Victorian Curriculum and Assessment Authority c) Victorian Combined Academic Authority d) Victorian Certificate of Academic Aptitude e) None of the above B
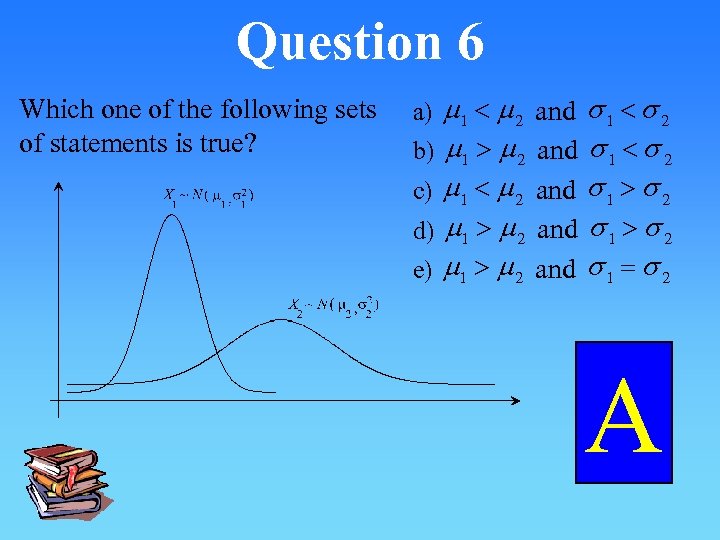 Question 6 Which one of the following sets of statements is true? a) m 1 < m 2 and s 1 < s 2 b) m 1 > m 2 and s 1 < s 2 c) m 1 < m 2 and s 1 > s 2 d) m 1 > m 2 and s 1 > s 2 e) m 1 > m 2 and s 1 = s 2 A
Question 6 Which one of the following sets of statements is true? a) m 1 < m 2 and s 1 < s 2 b) m 1 > m 2 and s 1 < s 2 c) m 1 < m 2 and s 1 > s 2 d) m 1 > m 2 and s 1 > s 2 e) m 1 > m 2 and s 1 = s 2 A
 Bonus Prize!!
Bonus Prize!!
 Question 8 where a, b and c are three different positive real numbers. The equation has exactly a) 1 real solution b) 2 distinct real solutions c) 3 distinct real solutions d) 4 distinct real solutions e) 5 distinct real solutions B
Question 8 where a, b and c are three different positive real numbers. The equation has exactly a) 1 real solution b) 2 distinct real solutions c) 3 distinct real solutions d) 4 distinct real solutions e) 5 distinct real solutions B
 Question 9 the sum of the For the equation solutions on the interval a) b) c) d) is e) E
Question 9 the sum of the For the equation solutions on the interval a) b) c) d) is e) E
 EXAMINATION 1 - FACTS, SKILLS AND APPLICATIONS TASK • Part A – 27 multiple-choice questions (27 marks) • Part B – short-answer questions (23 marks) • Time limit: – 15 minutes reading time – 90 minutes writing time
EXAMINATION 1 - FACTS, SKILLS AND APPLICATIONS TASK • Part A – 27 multiple-choice questions (27 marks) • Part B – short-answer questions (23 marks) • Time limit: – 15 minutes reading time – 90 minutes writing time
 EXAMINATION 2 - ANALYSIS TASK • Extended response questions – 4 questions (55 marks) • Time limit: – 15 minutes reading time – 90 minutes writing time
EXAMINATION 2 - ANALYSIS TASK • Extended response questions – 4 questions (55 marks) • Time limit: – 15 minutes reading time – 90 minutes writing time
 Question 1 The linear factors of the polynomial are ANSWER: B
Question 1 The linear factors of the polynomial are ANSWER: B
 Question 4 a) Expand fully
Question 4 a) Expand fully
 b) is exactly divisible by Find the value of a.
b) is exactly divisible by Find the value of a.
 Question 5 a)
Question 5 a)

 b)
b)
 Question 6 Coefficient of ANSWER: B
Question 6 Coefficient of ANSWER: B
 Question 7 Coefficient of ANSWER: D
Question 7 Coefficient of ANSWER: D
 Functions and Their Graphs Vertical line test - to determine whether a relation is a function A represents the DOMAIN
Functions and Their Graphs Vertical line test - to determine whether a relation is a function A represents the DOMAIN
![Interval Notation Square brackets [ ] – included Round brackets ( ) – excluded Interval Notation Square brackets [ ] – included Round brackets ( ) – excluded](https://present5.com/presentation/290fa787807015a00f94f0e5dacbb0b3/image-33.jpg) Interval Notation Square brackets [ ] – included Round brackets ( ) – excluded
Interval Notation Square brackets [ ] – included Round brackets ( ) – excluded
 Question 9 The range of the function with graph as shown is a) b) c) d) e) ANSWER: D
Question 9 The range of the function with graph as shown is a) b) c) d) e) ANSWER: D
 Maximal (or implied) Domain The largest possible domain for which the function is defined A function is undefined when: a) The denominator is equal to zero b) The square root of a negative number is present.
Maximal (or implied) Domain The largest possible domain for which the function is defined A function is undefined when: a) The denominator is equal to zero b) The square root of a negative number is present.
 Consider the function So the maximal domain is:
Consider the function So the maximal domain is:
 Question 10 This question requires EVERY option to be checked carefully. a) b) c) d) e)
Question 10 This question requires EVERY option to be checked carefully. a) b) c) d) e)
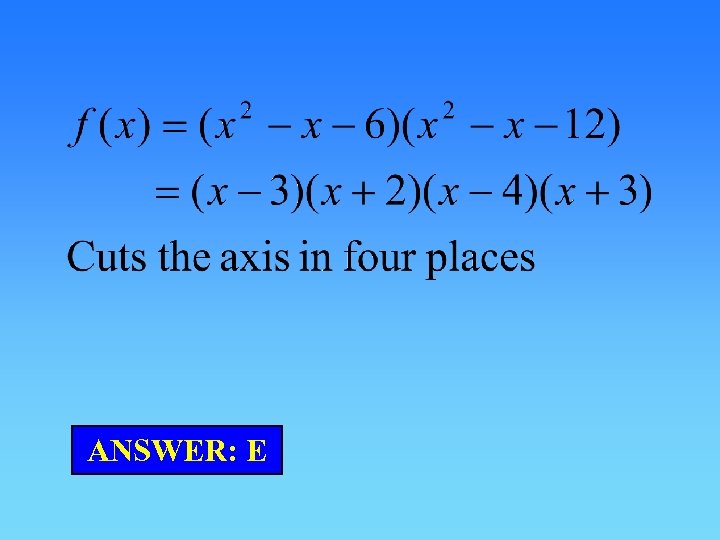 ANSWER: E
ANSWER: E
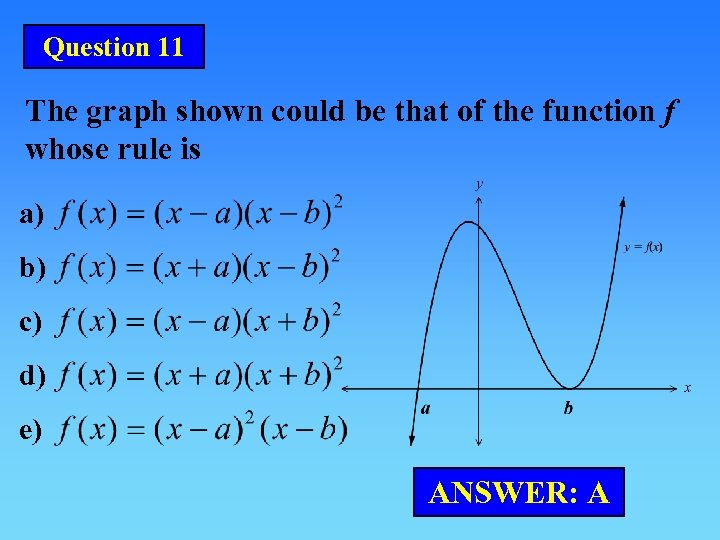 Question 11 The graph shown could be that of the function f whose rule is a) b) c) d) e) ANSWER: A
Question 11 The graph shown could be that of the function f whose rule is a) b) c) d) e) ANSWER: A
 Using Transformations When identifying the type of transformation that has been applied to a function it is essential to state each of the following: NATURE - Translation, Dilation, Reflection MAGNITUDE (or size) DIRECTION
Using Transformations When identifying the type of transformation that has been applied to a function it is essential to state each of the following: NATURE - Translation, Dilation, Reflection MAGNITUDE (or size) DIRECTION
 1. Translations a) Parallel to the x-axis – horizontal translation. b) Parallel to the y-axis – vertical translation. To avoid mistakes, let the bracket containing x equal zero and then solve for x. If the solution for x is positive – move the graph x units to the RIGHT. If the solution for x is negative – move the graph x units to the LEFT.
1. Translations a) Parallel to the x-axis – horizontal translation. b) Parallel to the y-axis – vertical translation. To avoid mistakes, let the bracket containing x equal zero and then solve for x. If the solution for x is positive – move the graph x units to the RIGHT. If the solution for x is negative – move the graph x units to the LEFT.
 2. Dilations a) Parallel to the y-axis – the dilation factor is the number outside the brackets. This can also be described as a dilation from the x-axis. b) Parallel to the x-axis – the dilation factor is the reciprocal of the coefficient of x. This can also be described as a dilation from the y-axis. Note: A dilation of a parallel to the y-axis is the parallel to the x-axis. same as a dilation of
2. Dilations a) Parallel to the y-axis – the dilation factor is the number outside the brackets. This can also be described as a dilation from the x-axis. b) Parallel to the x-axis – the dilation factor is the reciprocal of the coefficient of x. This can also be described as a dilation from the y-axis. Note: A dilation of a parallel to the y-axis is the parallel to the x-axis. same as a dilation of
 3. Reflections a) Reflection about the x-axis b) Reflection about the y-axis c) Reflection about both axes d) Reflection about the line
3. Reflections a) Reflection about the x-axis b) Reflection about the y-axis c) Reflection about both axes d) Reflection about the line
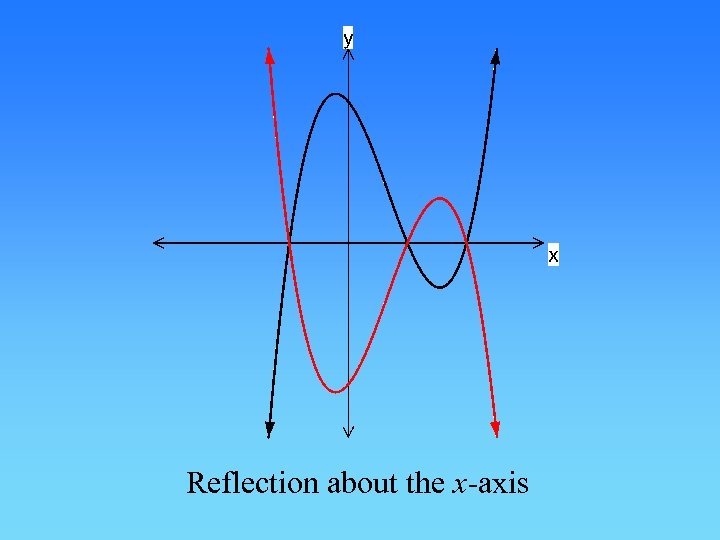 Reflection about the x-axis
Reflection about the x-axis
 Reflection about the y-axis
Reflection about the y-axis
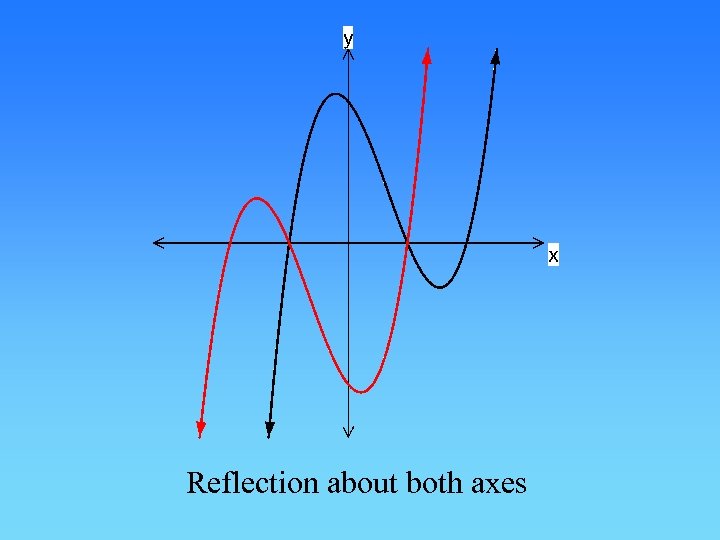 Reflection about both axes
Reflection about both axes
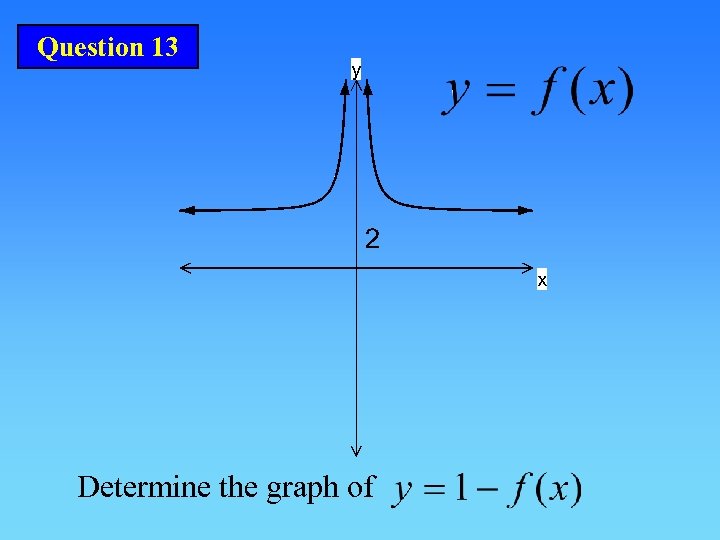 Question 13 Determine the graph of
Question 13 Determine the graph of
 Reflection about the x-axis
Reflection about the x-axis
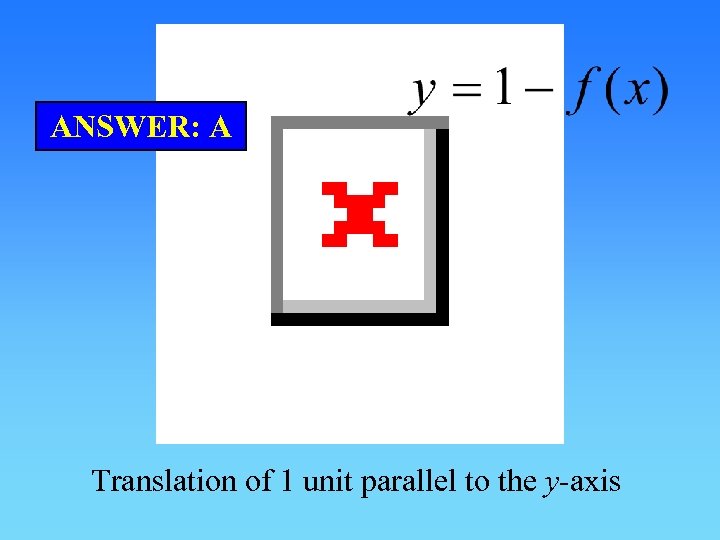 ANSWER: A Translation of 1 unit parallel to the y-axis
ANSWER: A Translation of 1 unit parallel to the y-axis
 EXTRA QUESTION The graph of the function f is obtained from the graph of the function with equation by a reflection in the y-axis followed by a dilation of 2 units from the x-axis. The rule for f is: a) Reflection: b) c) Dilation: d) e) ANSWER: E
EXTRA QUESTION The graph of the function f is obtained from the graph of the function with equation by a reflection in the y-axis followed by a dilation of 2 units from the x-axis. The rule for f is: a) Reflection: b) c) Dilation: d) e) ANSWER: E
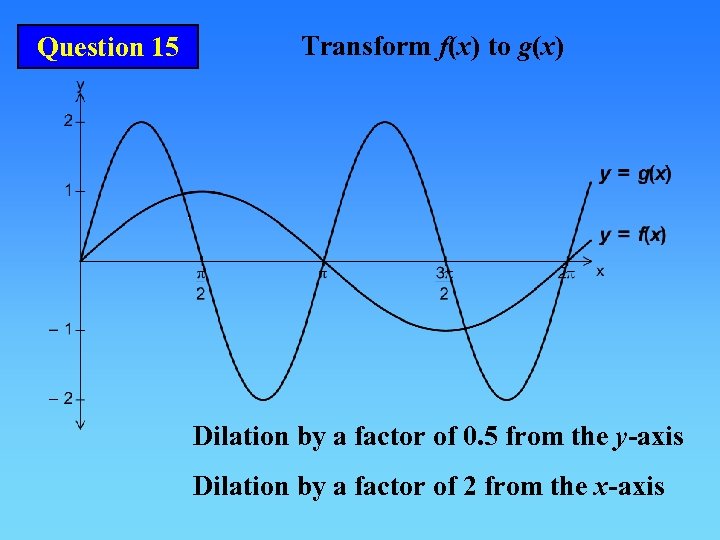 Question 15 Transform f(x) to g(x) Dilation by a factor of 0. 5 from the y-axis Dilation by a factor of 2 from the x-axis
Question 15 Transform f(x) to g(x) Dilation by a factor of 0. 5 from the y-axis Dilation by a factor of 2 from the x-axis
 Graphs of Rational Functions Question 16 The equations of the horizontal and vertical asymptotes of the graph with equation Vertical: Horizontal: ANSWER: E
Graphs of Rational Functions Question 16 The equations of the horizontal and vertical asymptotes of the graph with equation Vertical: Horizontal: ANSWER: E
 Inverse Functions Key features: Domain and range are interchanged Reflection about the line y = x The original function must be one-to-one
Inverse Functions Key features: Domain and range are interchanged Reflection about the line y = x The original function must be one-to-one
 To find the equation of an inverse function Step 1: Complete a Function, Domain, Range (FDR) table. Step 2: Interchange x and y in the given equation. Step 3: Transpose this equation to make y the subject. Step 4: Express the answer clearly stating the rule and the domain.
To find the equation of an inverse function Step 1: Complete a Function, Domain, Range (FDR) table. Step 2: Interchange x and y in the given equation. Step 3: Transpose this equation to make y the subject. Step 4: Express the answer clearly stating the rule and the domain.
 Question 17 ANSWER: A
Question 17 ANSWER: A
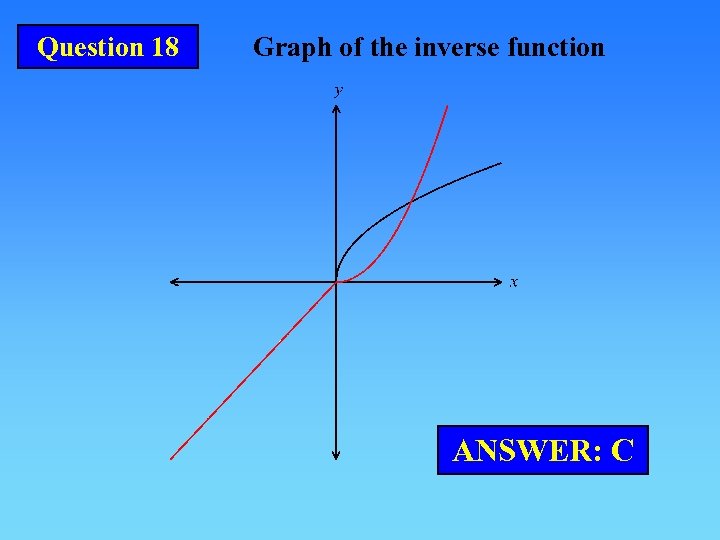 Question 18 Graph of the inverse function ANSWER: C
Question 18 Graph of the inverse function ANSWER: C
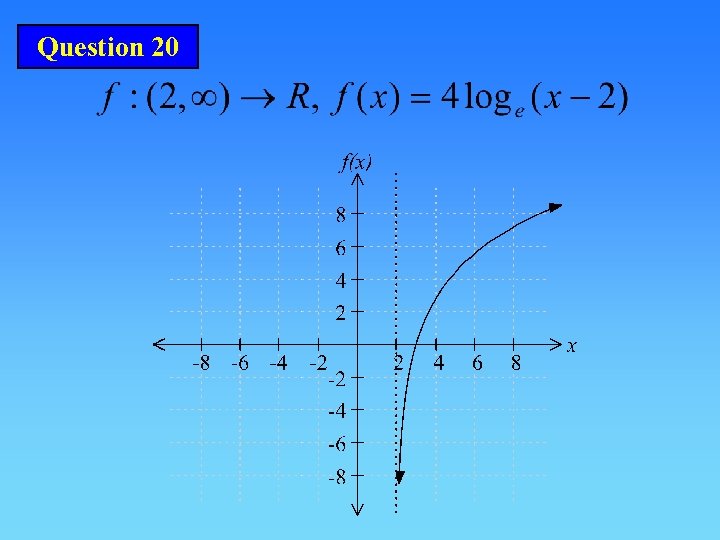 Question 20
Question 20
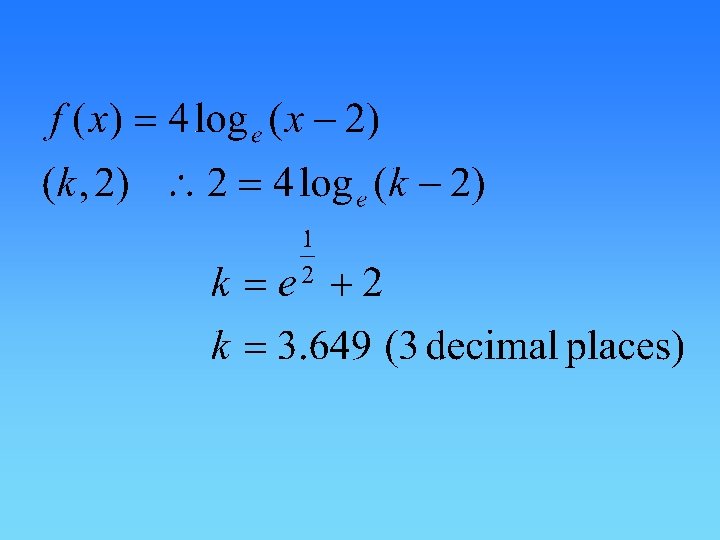
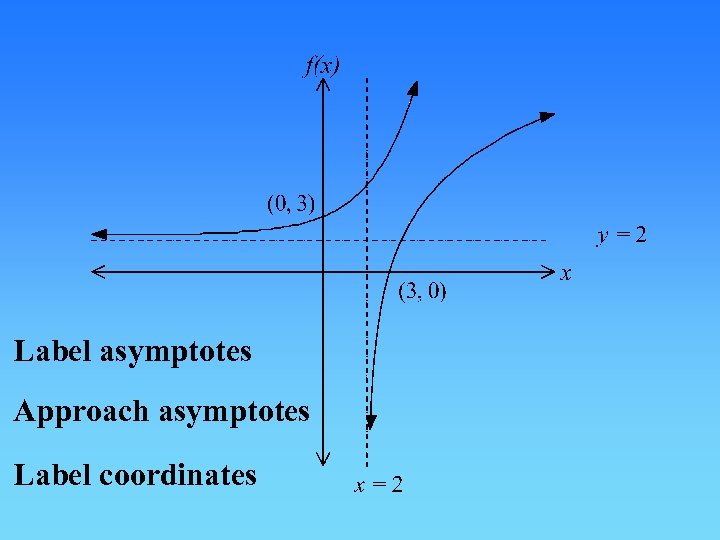 Label asymptotes Approach asymptotes Label coordinates
Label asymptotes Approach asymptotes Label coordinates
 Question 21 The equation relating x and y is most likely: ANSWER: E
Question 21 The equation relating x and y is most likely: ANSWER: E
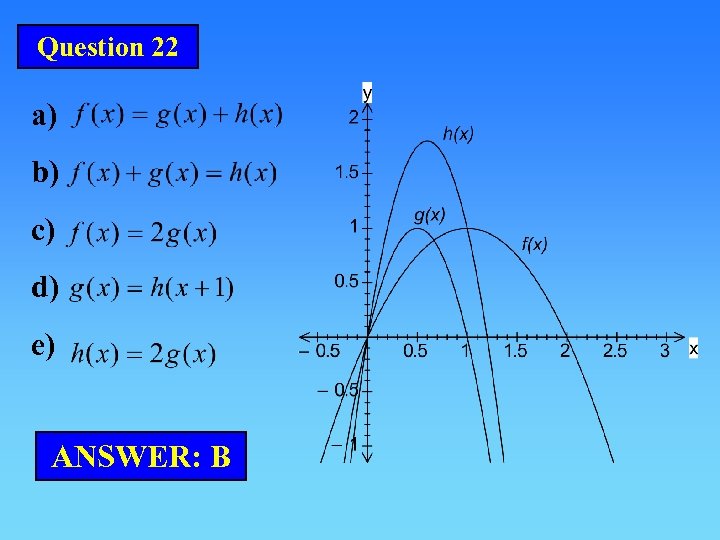 Question 22 a) b) c) d) e) ANSWER: B
Question 22 a) b) c) d) e) ANSWER: B
 Solving indicial equations Step 1: Use appropriate index laws to reduce both sides of the equation to one term. Step 2: Manipulate the equation so that either the bases or the powers are the same. Step 3: Equate the bases or powers. If this is not possible then take logarithms of both sides to either base 10 or base e.
Solving indicial equations Step 1: Use appropriate index laws to reduce both sides of the equation to one term. Step 2: Manipulate the equation so that either the bases or the powers are the same. Step 3: Equate the bases or powers. If this is not possible then take logarithms of both sides to either base 10 or base e.
 Question 23
Question 23
 Solving logarithmic equations Step 1: Use the logarithmic laws to reduce the given equation to two terms – one on each side of the equality sign. Step 2: Convert the logarithmic equation to indicial form. Step 3: Manipulate the given equation so that either the bases or the powers are the same.
Solving logarithmic equations Step 1: Use the logarithmic laws to reduce the given equation to two terms – one on each side of the equality sign. Step 2: Convert the logarithmic equation to indicial form. Step 3: Manipulate the given equation so that either the bases or the powers are the same.
 Step 4: Equate the bases or powers. If this is not possible then take logarithms of both sides to either base 10 or base e. Step 5: Check to make sure that the solution obtained does not cause the initial function to be undefined.
Step 4: Equate the bases or powers. If this is not possible then take logarithms of both sides to either base 10 or base e. Step 5: Check to make sure that the solution obtained does not cause the initial function to be undefined.
 Question 26 ANSWER: A
Question 26 ANSWER: A
 Question 27 ANSWER: D
Question 27 ANSWER: D
 Circular (Trigonometric) Functions Amplitude: a Period: Horizontal translation: c units in the negative x-direction Vertical translation: d units in the positive y-direction
Circular (Trigonometric) Functions Amplitude: a Period: Horizontal translation: c units in the negative x-direction Vertical translation: d units in the positive y-direction
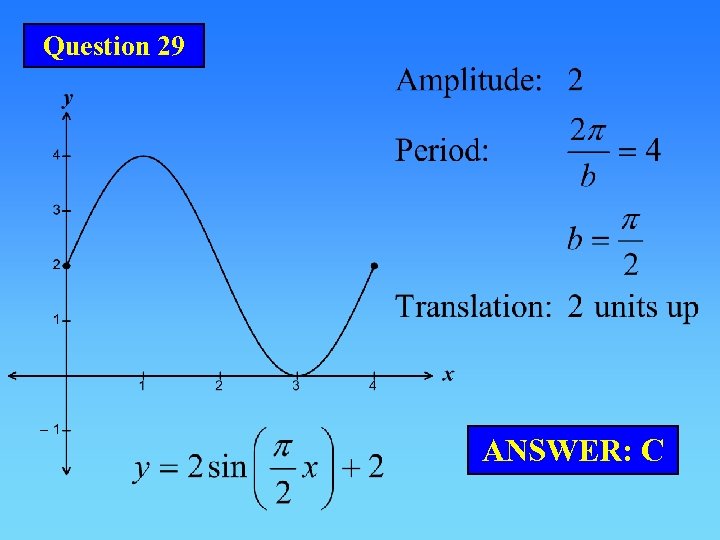 Question 29 ANSWER: C
Question 29 ANSWER: C
 Question 30 Amplitude: 2 Period: Range: ANSWER: B
Question 30 Amplitude: 2 Period: Range: ANSWER: B
 Question 31 a) b) c) d) e) ANSWER: C
Question 31 a) b) c) d) e) ANSWER: C
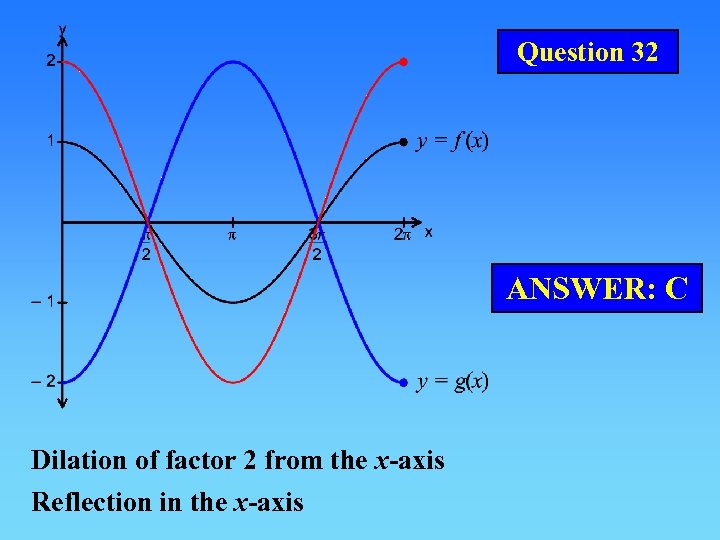 Question 32 ANSWER: C Dilation of factor 2 from the x-axis Reflection in the x-axis
Question 32 ANSWER: C Dilation of factor 2 from the x-axis Reflection in the x-axis
 Solving Trigonometric Equations • Put the expression in the form sin(ax) = B • Check the domain – modify as necessary. • Use the CAST diagram to mark the relevant quadrants. • Solve the angle as a first quadrant angle. • Use symmetry properties to find all solutions in the required domain. • Simplify to get x by itself.
Solving Trigonometric Equations • Put the expression in the form sin(ax) = B • Check the domain – modify as necessary. • Use the CAST diagram to mark the relevant quadrants. • Solve the angle as a first quadrant angle. • Use symmetry properties to find all solutions in the required domain. • Simplify to get x by itself.
 Question 33 a) b)
Question 33 a) b)
 Question 34 ANSWER: E
Question 34 ANSWER: E
 Question 35 ANSWER: E
Question 35 ANSWER: E
 Question 36 a) Analysis Question
Question 36 a) Analysis Question
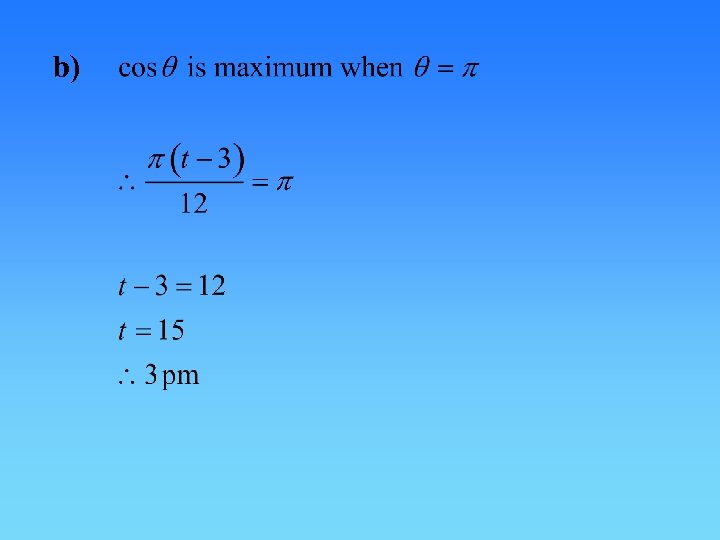 b)
b)
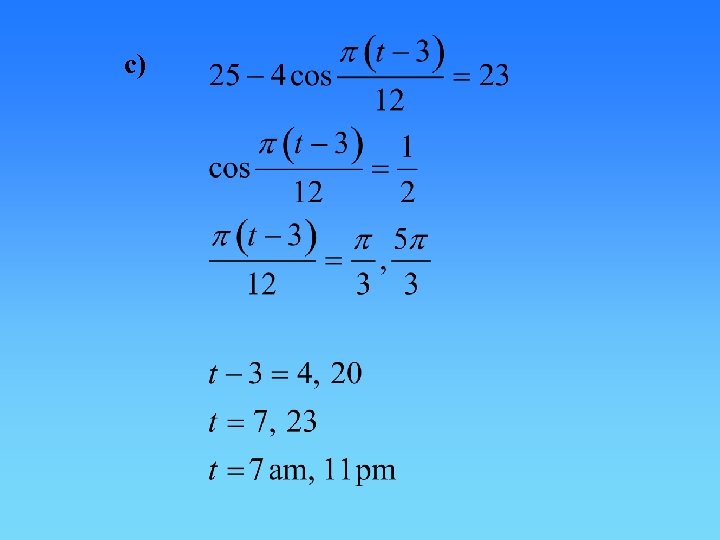 c)
c)
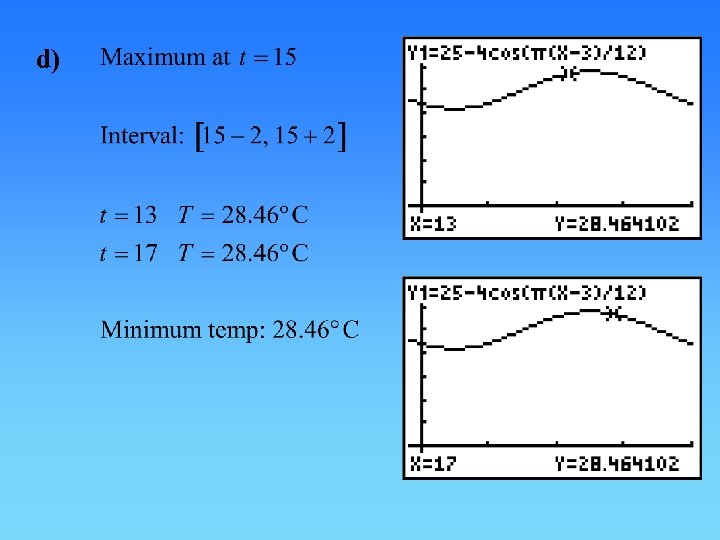 d)
d)
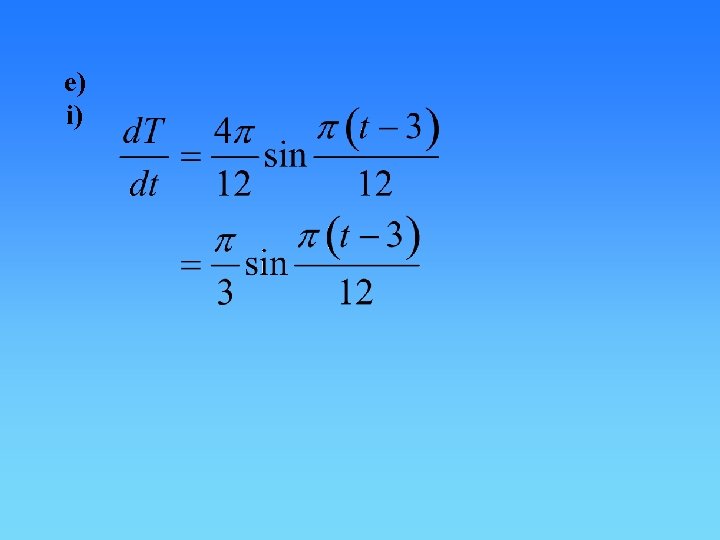 e) i)
e) i)
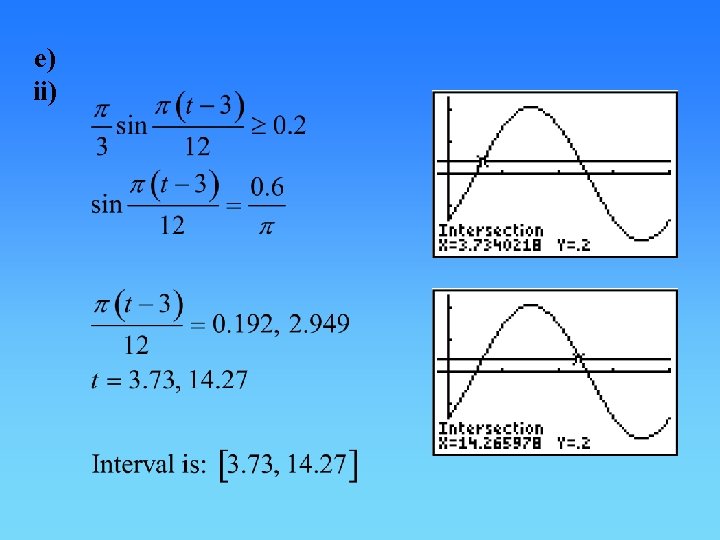 e) ii)
e) ii)
 DIFFERENTIAL CALCULUS Chain Rule: Product Rule: Quotient Rule:
DIFFERENTIAL CALCULUS Chain Rule: Product Rule: Quotient Rule:
 Further Rules of Differentiation Square Root Functions
Further Rules of Differentiation Square Root Functions
 Further Rules of Differentiation Trigonometric Functions
Further Rules of Differentiation Trigonometric Functions
 Further Rules of Differentiation Logarithmic Functions
Further Rules of Differentiation Logarithmic Functions
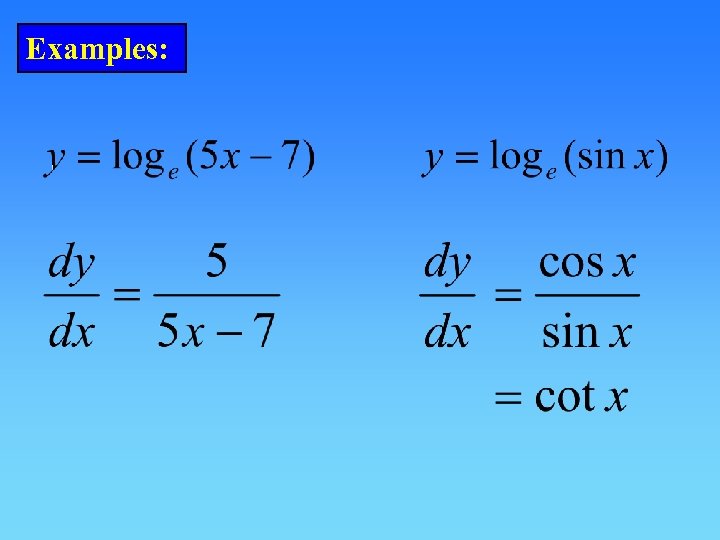 Examples:
Examples:
 Further Rules of Differentiation Exponential Functions
Further Rules of Differentiation Exponential Functions
 Examples:
Examples:
 Question 37 ANSWER: D
Question 37 ANSWER: D
 Question 39 ANSWER: A
Question 39 ANSWER: A
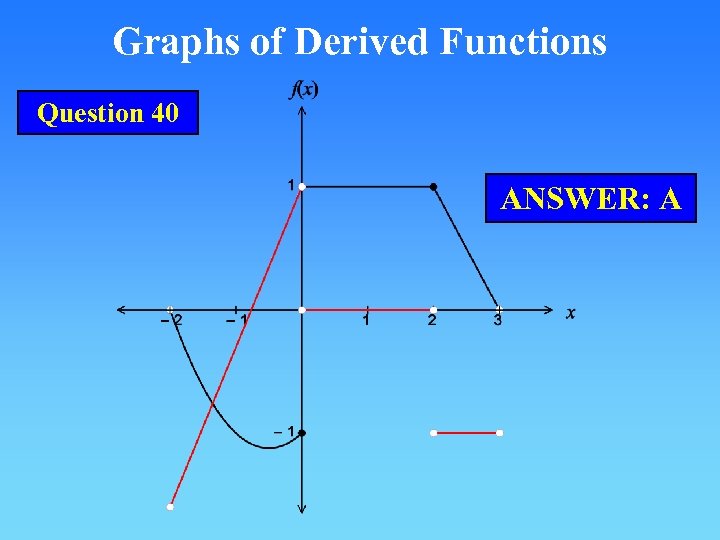 Graphs of Derived Functions Question 40 ANSWER: A
Graphs of Derived Functions Question 40 ANSWER: A
 Question 42 ANSWER: C
Question 42 ANSWER: C
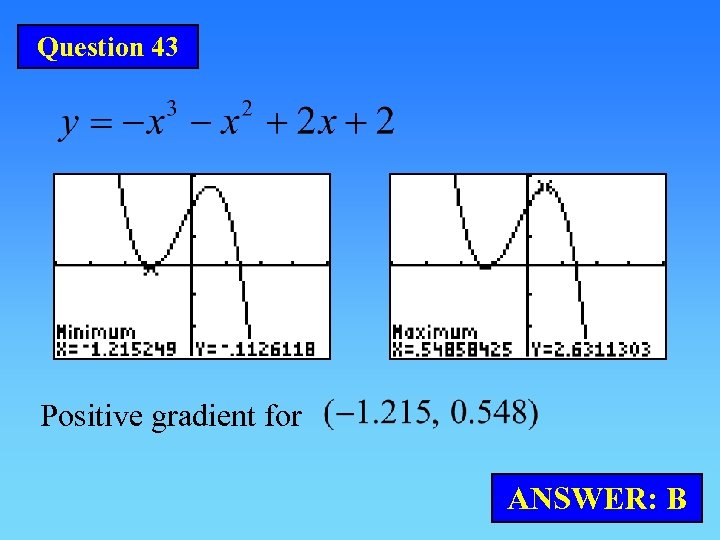 Question 43 Positive gradient for ANSWER: B
Question 43 Positive gradient for ANSWER: B
 Approximations Question 44 ANSWER: B
Approximations Question 44 ANSWER: B
 Question 46 a) Analysis Question b)
Question 46 a) Analysis Question b)
 c) Use CALCULUS to find the EXACT values of the COORDINATES of the turning point.
c) Use CALCULUS to find the EXACT values of the COORDINATES of the turning point.
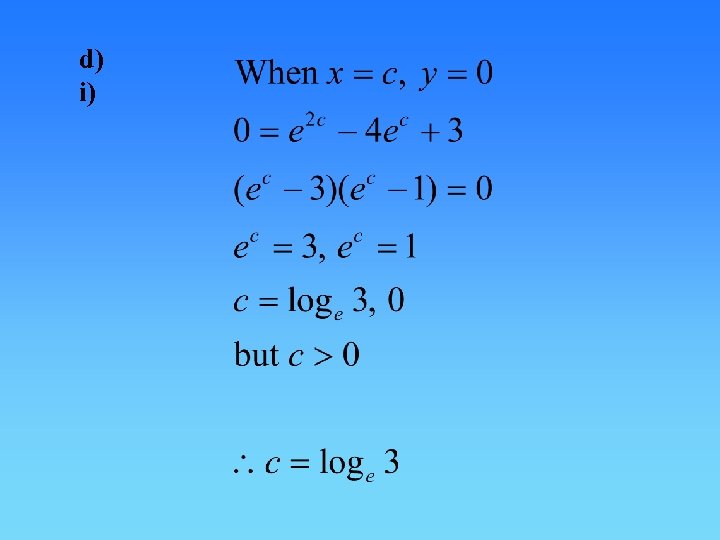 d) i)
d) i)
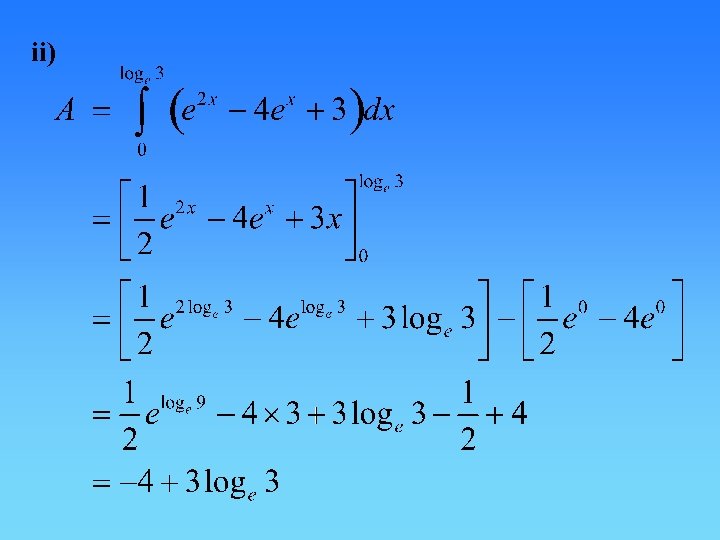 ii)
ii)
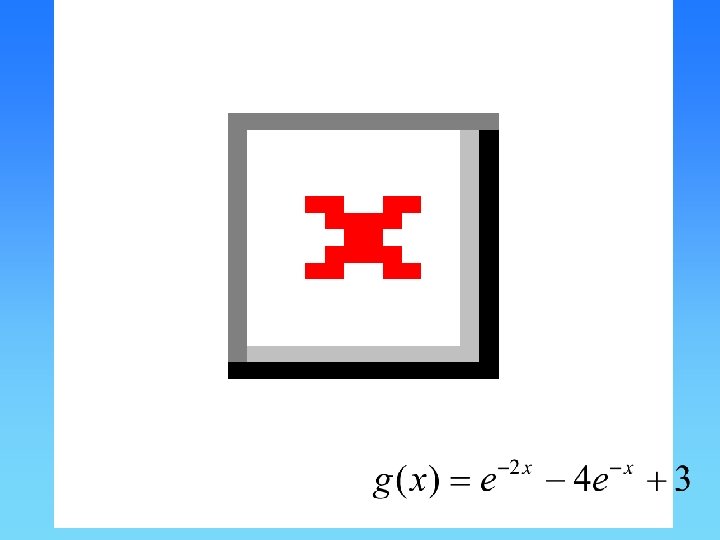
 Antidifferentiation and Integral Calculus
Antidifferentiation and Integral Calculus
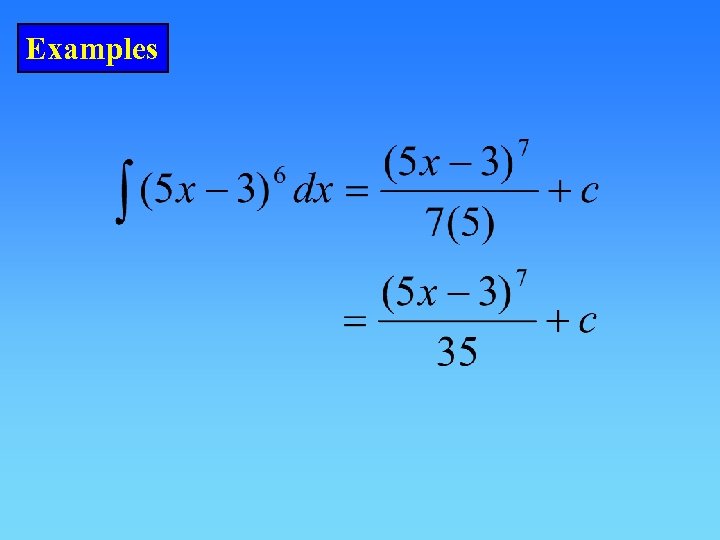 Examples
Examples

 Question 47 ANSWER: E
Question 47 ANSWER: E
 Rules of Antidifferentiation Trigonometric Functions
Rules of Antidifferentiation Trigonometric Functions
 Rules of Antidifferentiation Exponential Functions
Rules of Antidifferentiation Exponential Functions
 Rules of Antidifferentiation Logarithmic Functions
Rules of Antidifferentiation Logarithmic Functions
 Examples
Examples
 Definite Integrals
Definite Integrals
 Example
Example
 Properties of Definite Integrals Question 49 ANSWER: D
Properties of Definite Integrals Question 49 ANSWER: D
 EXTRA QUESTION If then is equal to:
EXTRA QUESTION If then is equal to:
 Integration by recognition
Integration by recognition
 Question 50 ANSWER: B
Question 50 ANSWER: B
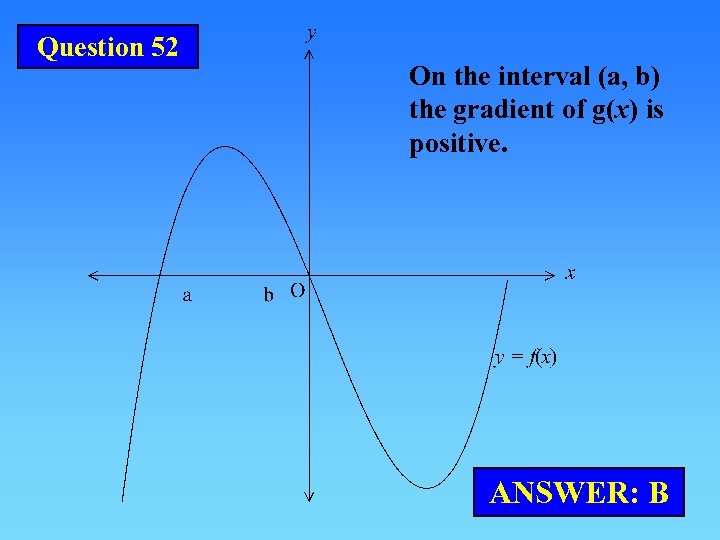 Question 52 On the interval (a, b) the gradient of g(x) is positive. ANSWER: B
Question 52 On the interval (a, b) the gradient of g(x) is positive. ANSWER: B
 Calculating Area • Sketch a graph of the function, labelling all x-intercepts. • Shade in the region required. • Divide the area into parts above the x-axis and parts below the x-axis. • Find the integral of each of the separate sections, using the x-intercepts as the terminals of integration. • Subtract the negative areas from the positive areas to obtain the total area.
Calculating Area • Sketch a graph of the function, labelling all x-intercepts. • Shade in the region required. • Divide the area into parts above the x-axis and parts below the x-axis. • Find the integral of each of the separate sections, using the x-intercepts as the terminals of integration. • Subtract the negative areas from the positive areas to obtain the total area.
 Question 53 The total area of the shaded region is given by: ANSWER: C
Question 53 The total area of the shaded region is given by: ANSWER: C
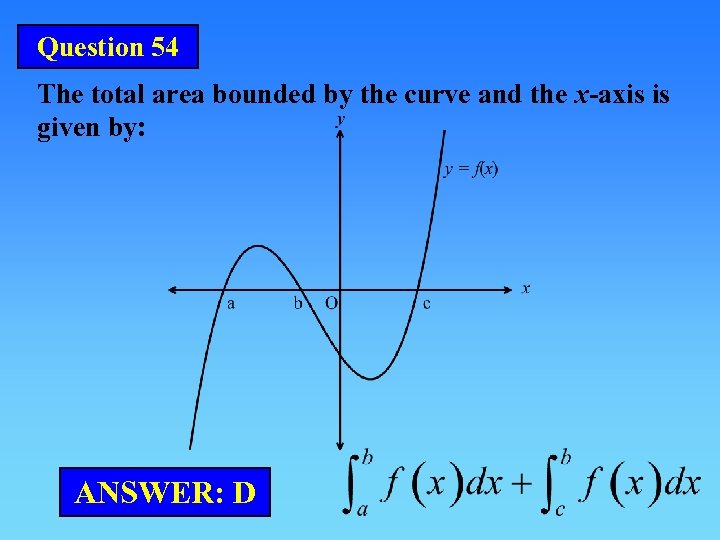 Question 54 The total area bounded by the curve and the x-axis is given by: ANSWER: D
Question 54 The total area bounded by the curve and the x-axis is given by: ANSWER: D
 Question 55 a)
Question 55 a)
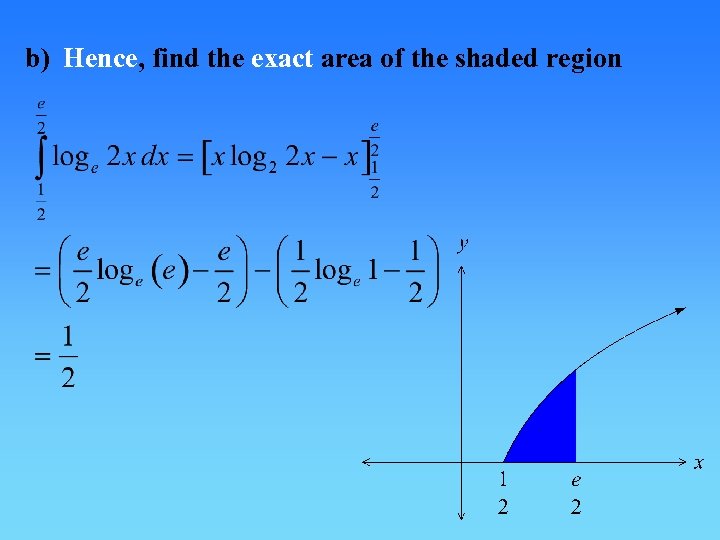 b) Hence, find the exact area of the shaded region
b) Hence, find the exact area of the shaded region
 Area between curves
Area between curves
 Method • Sketch the curves, locating the points of intersection. • Shade in the required region. • If the terminals of integration are not given – use the points of intersection. • Check to make sure that the upper curve remains as the upper curve throughout the required region. If this is not the case then the area must be divided into separate sections. • Evaluate the area.
Method • Sketch the curves, locating the points of intersection. • Shade in the required region. • If the terminals of integration are not given – use the points of intersection. • Check to make sure that the upper curve remains as the upper curve throughout the required region. If this is not the case then the area must be divided into separate sections. • Evaluate the area.
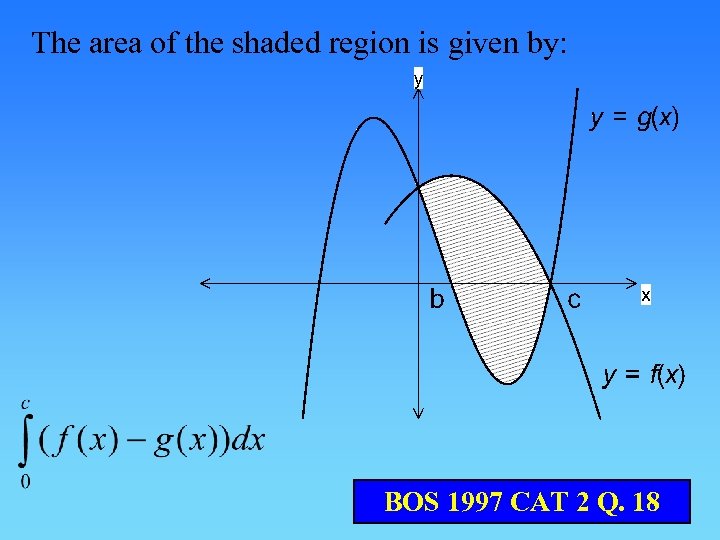 The area of the shaded region is given by: BOS 1997 CAT 2 Q. 18
The area of the shaded region is given by: BOS 1997 CAT 2 Q. 18
 Question 56 Find the exact area of the shaded region
Question 56 Find the exact area of the shaded region

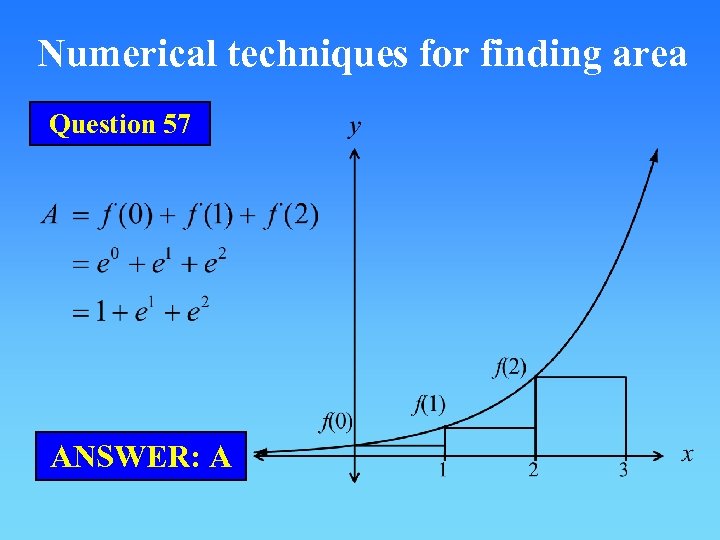 Numerical techniques for finding area Question 57 ANSWER: A
Numerical techniques for finding area Question 57 ANSWER: A
 Question 58 a) Analysis Question
Question 58 a) Analysis Question
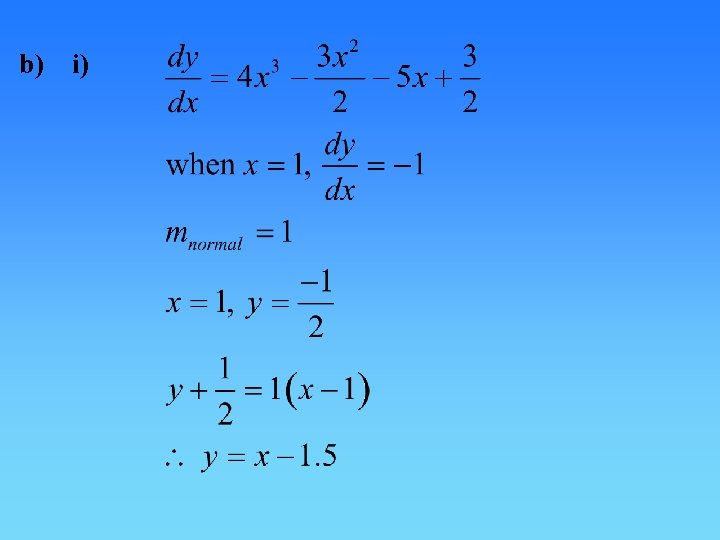 b) i)
b) i)
 b) ii) A repeated root at x = -1 indicates that the normal is a tangent to the curve at this point.
b) ii) A repeated root at x = -1 indicates that the normal is a tangent to the curve at this point.
 c) i)
c) i)
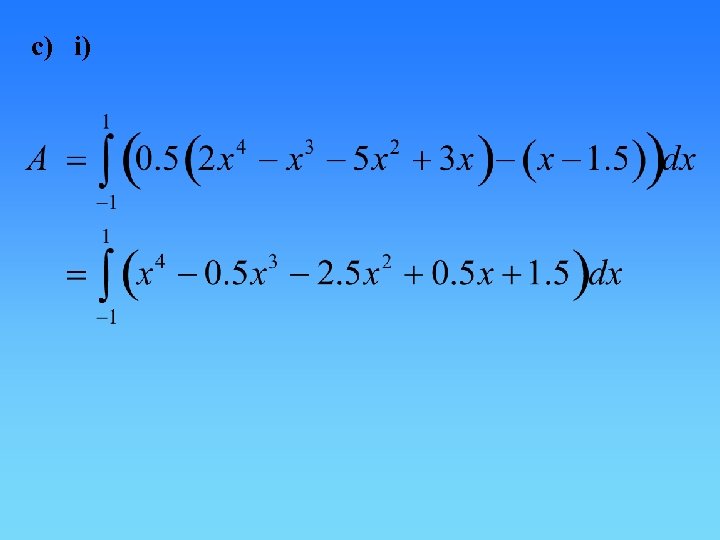 c) i)
c) i)
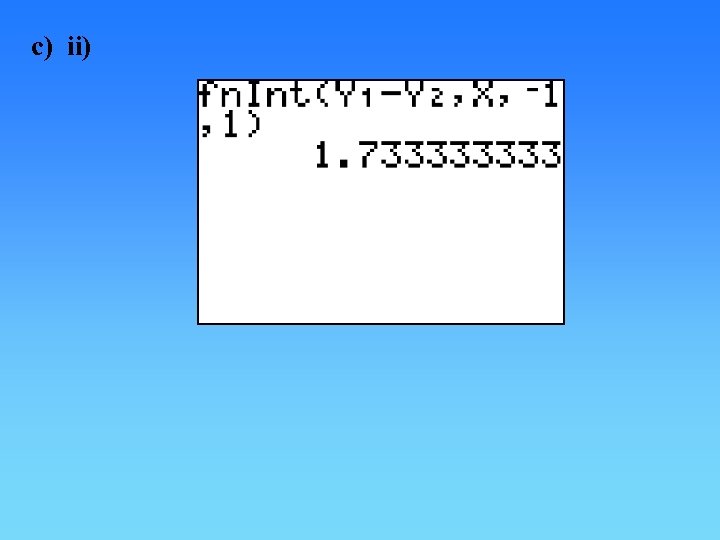 c) ii)
c) ii)
 Discrete Random Variables A discrete random variable takes only distinct or discrete values and nothing in between. Discrete variables are treated using either discrete, binomial or hypergeometric distributions. A continuous random variable can take any value within a given domain. These values are usually obtained through measurement of a quantity. Continuous variables are treated using normal distributions.
Discrete Random Variables A discrete random variable takes only distinct or discrete values and nothing in between. Discrete variables are treated using either discrete, binomial or hypergeometric distributions. A continuous random variable can take any value within a given domain. These values are usually obtained through measurement of a quantity. Continuous variables are treated using normal distributions.
 Expected value and expectation theorems
Expected value and expectation theorems
 Variance and Standard Deviation
Variance and Standard Deviation
 Question 60 Melissa constructs a spinner that will fall onto one of the numbers 1 to 5 with the following probabilities. The mean and standard deviation of the number that the spinner falls onto are, correct to two decimal places,
Question 60 Melissa constructs a spinner that will fall onto one of the numbers 1 to 5 with the following probabilities. The mean and standard deviation of the number that the spinner falls onto are, correct to two decimal places,
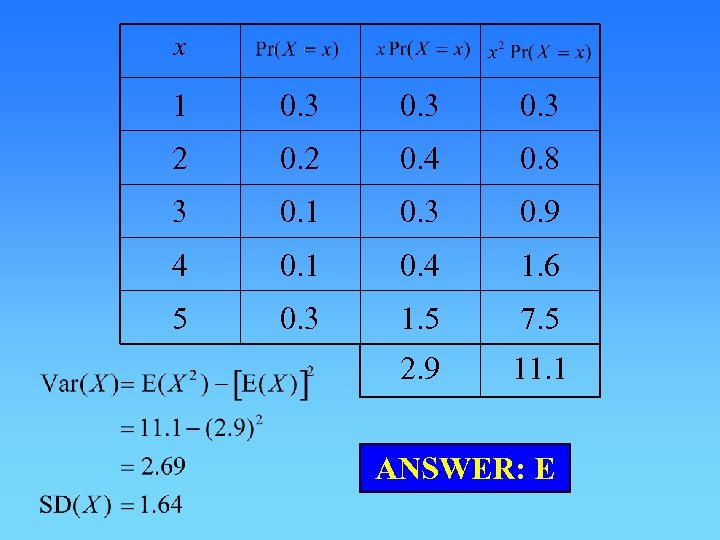 x 1 0. 3 2 0. 4 0. 8 3 0. 1 0. 3 0. 9 4 0. 1 0. 4 1. 6 5 0. 3 1. 5 7. 5 2. 9 11. 1 ANSWER: E
x 1 0. 3 2 0. 4 0. 8 3 0. 1 0. 3 0. 9 4 0. 1 0. 4 1. 6 5 0. 3 1. 5 7. 5 2. 9 11. 1 ANSWER: E
 The Binomial Distribution
The Binomial Distribution
 Question 61 In a two-week period of ten school days, the probability that the traffic lights have been green on exactly nine occasions is: ANSWER: A
Question 61 In a two-week period of ten school days, the probability that the traffic lights have been green on exactly nine occasions is: ANSWER: A
 Question 63 ANSWER: A
Question 63 ANSWER: A
 The Hypergeometric Distribution
The Hypergeometric Distribution

 Question 64 A team of four is selected from six women and four men. What is the probability that the team consists of exactly one woman and three men. ANSWER: A
Question 64 A team of four is selected from six women and four men. What is the probability that the team consists of exactly one woman and three men. ANSWER: A
 Question 65 A jar contains fifteen jellybeans of which twelve are green. Four jelly beans are taken from the jar at random and eaten, calculate
Question 65 A jar contains fifteen jellybeans of which twelve are green. Four jelly beans are taken from the jar at random and eaten, calculate
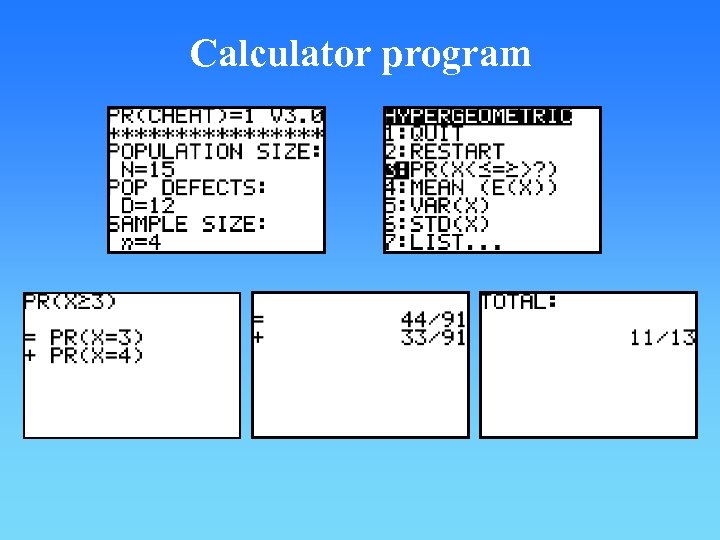 Calculator program
Calculator program
 The Normal Distribution The mean, mode and median are the same. The total area under the curve is one unit.
The Normal Distribution The mean, mode and median are the same. The total area under the curve is one unit.
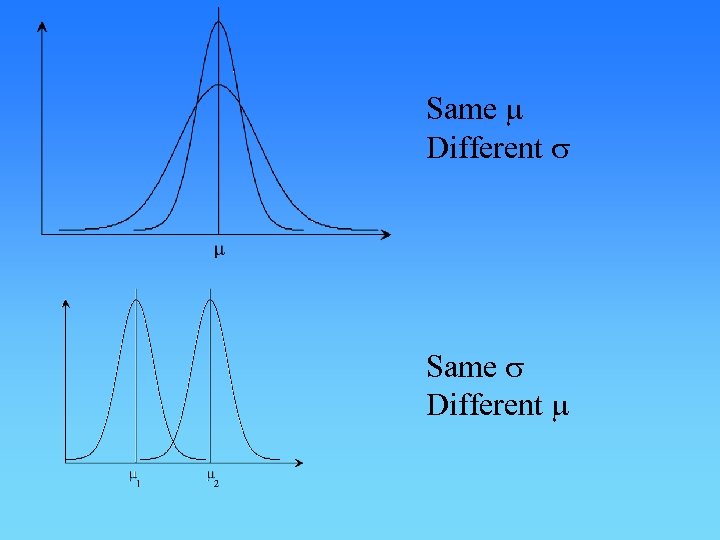 Same m Different s Same s Different m
Same m Different s Same s Different m
 Question 67 Which one of the following sets of statements is true? ANSWER: A
Question 67 Which one of the following sets of statements is true? ANSWER: A
 Method • Draw a diagram, clearly labelling the mean. • Shade the region required. • Determine the z value which corresponds to the value of x by using • Use the cumulative normal distribution table to find the required probability.
Method • Draw a diagram, clearly labelling the mean. • Shade the region required. • Determine the z value which corresponds to the value of x by using • Use the cumulative normal distribution table to find the required probability.
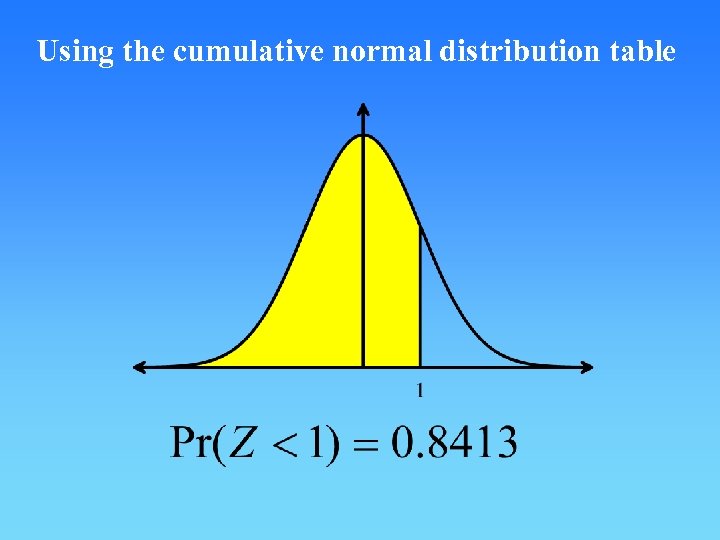 Using the cumulative normal distribution table
Using the cumulative normal distribution table
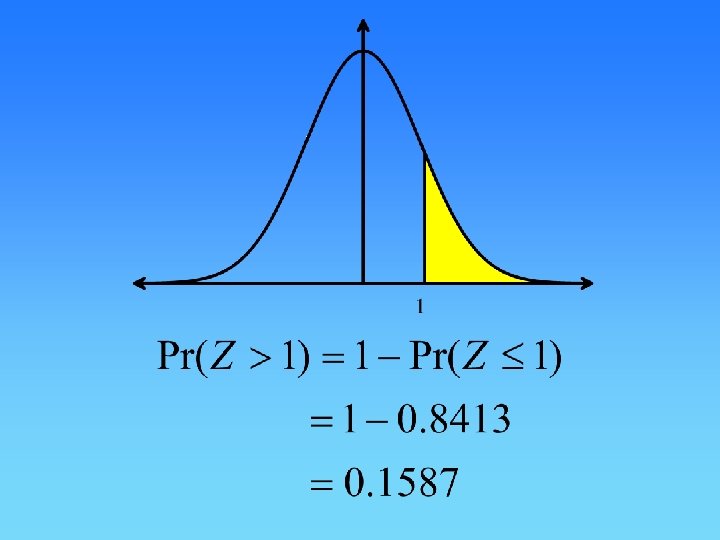
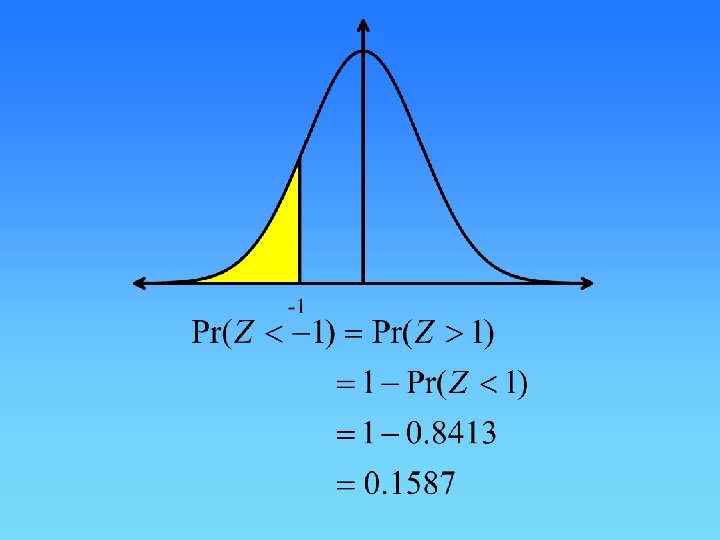
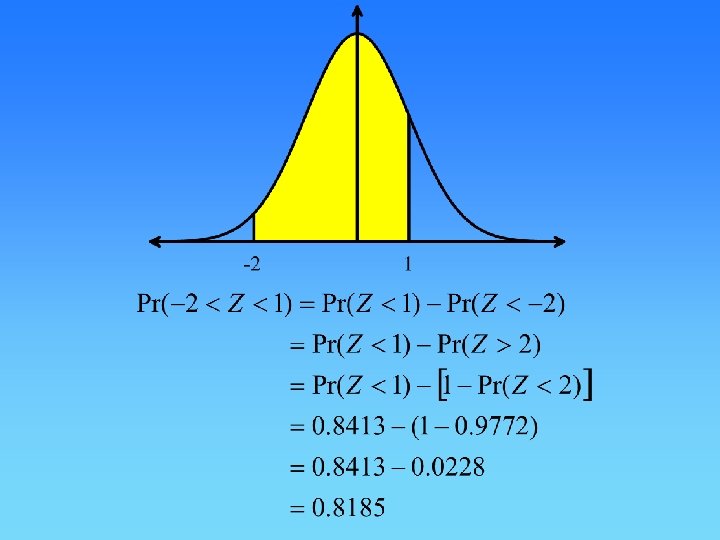
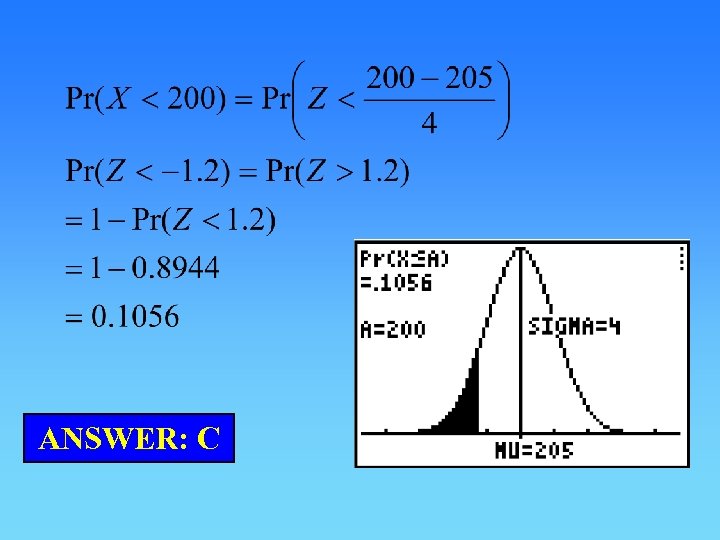
 Question 68 The mass of fruit jubes, in a packet labelled as containing 200 grams, has been found to be normally distributed with a mean of 205 grams and a standard deviation of 4 grams. The percentage of packets that contain less than 200 grams is, correct to one decimal place,
Question 68 The mass of fruit jubes, in a packet labelled as containing 200 grams, has been found to be normally distributed with a mean of 205 grams and a standard deviation of 4 grams. The percentage of packets that contain less than 200 grams is, correct to one decimal place,
 ANSWER: C
ANSWER: C
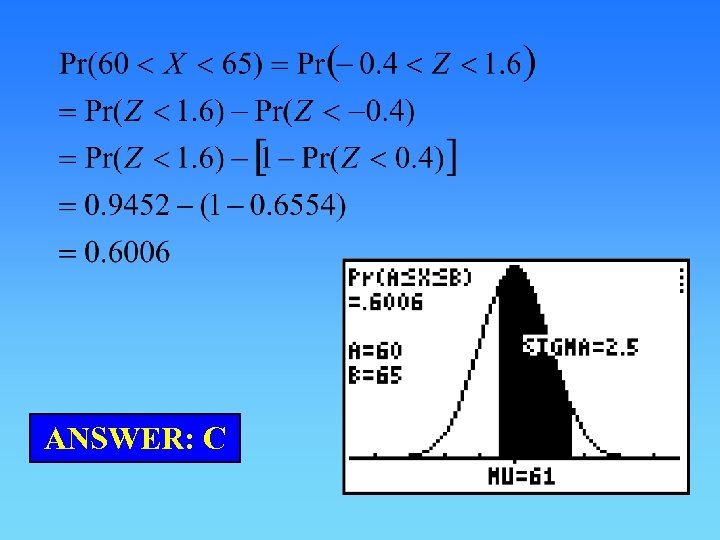
 Question 71 The eggs laid by a particular breed of chicken have a mass which is normally distributed with a mean of 61 g and a standard deviation of 2. 5 g. The probability, correct to four decimal places, that a single egg has a mass between 60 g and 65 g is
Question 71 The eggs laid by a particular breed of chicken have a mass which is normally distributed with a mean of 61 g and a standard deviation of 2. 5 g. The probability, correct to four decimal places, that a single egg has a mass between 60 g and 65 g is
 ANSWER: C
ANSWER: C
 Applications of the normal distribution • Draw a diagram, clearly shading the region that corresponds to the given probability. • Use the symmetry properties of the curve to write down the appropriate z value. • Use the inverse normal distribution table (or graphic calculator) to find the required probability and the corresponding z value. • Use the relationship calculate the required x value. to
Applications of the normal distribution • Draw a diagram, clearly shading the region that corresponds to the given probability. • Use the symmetry properties of the curve to write down the appropriate z value. • Use the inverse normal distribution table (or graphic calculator) to find the required probability and the corresponding z value. • Use the relationship calculate the required x value. to
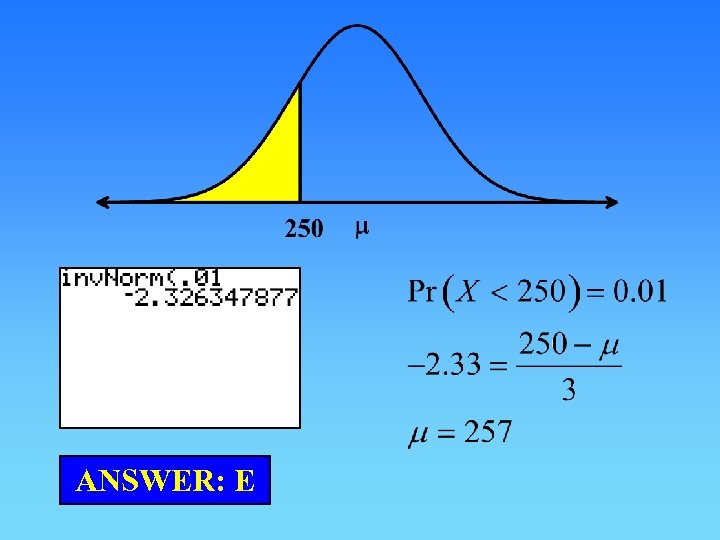
 Question 72 Black Mountain coffee is sold in packets labeled as being of 250 grams weight. The packing process produces packets whose weight is normally distributed with a standard deviation of 3 grams. In order to guarantee that only 1% of packets are under the labeled weight, the actual mean weight (in grams) would be required to be closest to a) 243 b) 247 c) 250 d) 254 e) 257
Question 72 Black Mountain coffee is sold in packets labeled as being of 250 grams weight. The packing process produces packets whose weight is normally distributed with a standard deviation of 3 grams. In order to guarantee that only 1% of packets are under the labeled weight, the actual mean weight (in grams) would be required to be closest to a) 243 b) 247 c) 250 d) 254 e) 257
 ANSWER: E
ANSWER: E
 Question 74
Question 74
 Question 75 a) b) Analysis Question
Question 75 a) b) Analysis Question
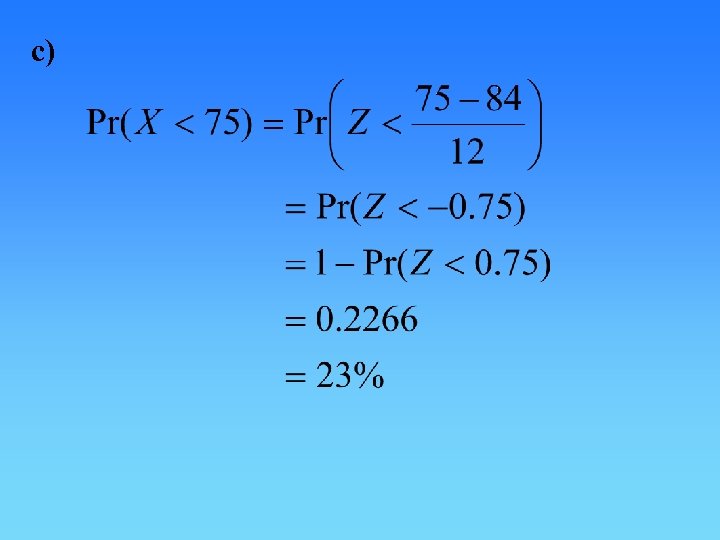 c)
c)
 d)
d)
 e) Conditional probability
e) Conditional probability
 f)
f)
 g)
g)
 THE FINAL RESULT
THE FINAL RESULT
 www. mav. vic. edu. au www. homepages. ihug. com. au/~mvswan
www. mav. vic. edu. au www. homepages. ihug. com. au/~mvswan


